第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「磁気エネルギー」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「磁気エネルギー」の過去問題も解説しています。
磁気エネルギー
コイルに電流が流れると、コイルの内部には磁束が発生します。磁束によって作られた磁界はエネルギーを蓄えることができます。巻数 $N$[回]のコイルに電流 $I$[A]を流したとき、磁束 $ϕ$[Wb]の磁界が蓄えることができる磁気エネルギー $W$[J](単位:ジュール[J])は、次の式で求めることができます。
磁気エネルギー $W$ を求める公式①
$W=\displaystyle \frac{ 1 }{ 2 }(ϕ×NI)$[J]
$W$[J]:磁気エネルギー
$ϕ$[Wb]:磁束
$N$[回]:巻数
$I$[A]:電流
磁気回路のオームの法則は次のように表されます。
$R_{ m }=\displaystyle \frac{ NI}{ ϕ }=\displaystyle \frac{ l}{ μS}$
$ ϕ =\displaystyle\frac{μSNI}{l }$[Wb]
自己インダクタンス $L$(単位 ヘンリー[H])は次のように表します。
$L=\displaystyle\frac{μSN^2}{l}$[H]
これらの式を使って
$W=\displaystyle \frac{ 1 }{ 2 }( ϕ ×NI)$[J]
を変形すると
磁気エネルギー $W$ を求める公式②
$W=\displaystyle \frac{ 1 }{ 2 }( ϕ ×NI)=\displaystyle \frac{ 1 }{ 2 }LI^2$[J]
$W$[J]:磁気エネルギー
$ϕ$[Wb]:磁束
$N$[回]:巻数
$I$[A]:電流
$L$[H]:自己インダクタンス
電験三種-理論の過去問解説:磁気エネルギー
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1997年(平成9年)問3【電験理論の過去問題】
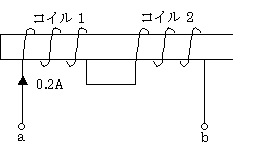
鉄心に巻かれたコイル1及びコイル2を図のように接続し、0.2[A]の直流電流を流した場合、端子ab間に蓄えられるエネルギーの値[J]として、正しいのは次のうちどれか。ただし、両コイルの自己インダクタンスは、それぞれ L1=1[H]、L2=4[H]とし、相互インダクタンスは、M=1.5[H]とする。
(1) 0.08 (2) 0.1 (3) 0.12 (4) 0.14 (5) 0.16
1次コイルと2次コイルがつくる磁界が同じ向きになる接続方法を和動接続といい、合成インダクタンスは次のようになります。
$L=L_1+L_2+2M =1+4+2×1.5=8$[H]
磁気エネルギー W[J]は
$W=\displaystyle \frac{ 1 }{ 2 }LI^2=\displaystyle \frac{ 1 }{ 2 }×8×0.2^2=0.16$[J]
答え (5)
2009年(平成21年)問3【電験理論の過去問題】
次の文章は、コイルの磁束鎖交数とコイルに蓄えられる磁気エネルギーについて述べたものである。
インダクタンス 1[mH]のコイルに直流電流 10[A]が流れている。このコイルの磁束鎖交数 Ψ1[Wb]は( ア )である。また、コイルに蓄えられている磁気エネルギー W1[J]は( イ )[J]である。
次に、コイルに流れる直流電流を 30[A]とすると、磁束鎖交数 Ψ2[Wb]と蓄えられる磁気エネルギーW2[J]はそれぞれ( ウ )となる。
上記の記述の空白箇所(ア),(イ)及び(ウ)に当てはまる語句又は数値として、正しいものを組み合わせたのは次のうちどれか。

N 巻のコイルに $I$[A]の電流を流したとき、磁束が $ ϕ $[Wb]生じたときの磁束鎖交数は $Ψ=LI$ なので、
$\begin{eqnarray}Ψ_1&=&LI\\\\&=&1×10^{-3}×10\\\\&=&1×10^{-2}[Wb]\end{eqnarray}$
$\begin{eqnarray}W_1&=&\displaystyle \frac{ 1 }{ 2 }LI^2\\\\&=&\displaystyle \frac{ 1 }{ 2 }×1×10^{-3}×10^2\\\\&=&5×10^{-2}[J]\end{eqnarray}$
$\begin{eqnarray}Ψ_2&=&LI\\\\&=&1×10^{-3}×30\\\\&=&3×10^{-2}[Wb]\end{eqnarray}$
$\begin{eqnarray}W_3&=&\displaystyle \frac{ 1 }{ 2 }LI^2\\\\&=&\displaystyle \frac{ 1 }{ 2 }×1×10^{-3}×30^2\\\\&=&45×10^{-2}[J]\end{eqnarray}$
答え (2)
電験三種の理論科目に出題される「電磁気分野」のページ
1.磁力線と磁束
2.アンペールの法則
3.フレミングの左手の法則
4.電流が磁界から受ける力
5.ヒステリシス曲線と損失
6.電磁誘導(レンツの法則とファラデーの法則)
7.自己インダクタンス
8.相互インダクタンス
9.磁気エネルギー






