第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される正弦波交流の波形について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された正弦波交流の波形の過去問題も解説しています。
正弦波交流の波形
時間とともに大きさおよび向きが一定の周期ごとに変化する電流や電圧を「交流]といいます。 交流のうち三角関数($sin$ または $cos$)で表されるものを「正弦波交流]と呼びます。
$x$ 軸を時間、$y$ 軸を電圧として正弦波交流の変化を調べると、交流電圧のグラフは次の図のような波形になります。
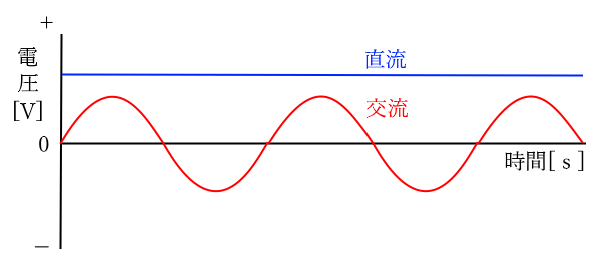
正弦波交流の電圧は一時的にゼロになったり、マイナスになったりする場合があります。
周期と周波数
正弦波交流は、同じ波形を繰り返します。一つの変化を繰り返す時間を「周期」 $T$(単位:秒[s])といいます。また、1 秒間に同じ波形を繰り返す回数を「周波数」 $f$(単位:ヘルツ[Hz])といいます。周期 $T$ と、周波数 $f$ の関係は次のようになります。
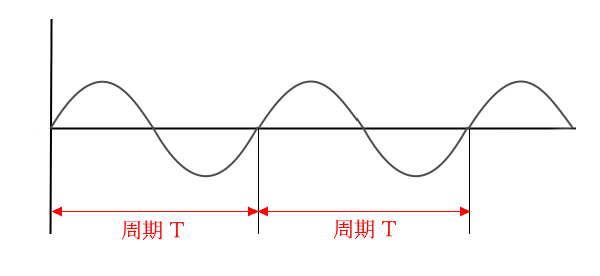
周波数と周期の関係
$T=\displaystyle \frac{ 1 }{ f }$
$T$[秒]:周期
$f$[Hz]:周波数
円運動
円運動をしている物体の速度は、1秒間に回転する角度で表すことができます。これを「角速度」といい、$ω$(読み:オメガ)で表します。また、$ω$ の単位は、rad/s(ラジアン毎秒)を用います。
角速度 $ω$[rad/s]で円運動をする物体の $t$ 秒後の回転角度は、$ωt$[rad]となります。角度の単位に用いられる[rad]は、半径 $r$ の円において、$r$ と等しい長さ $l$ の円弧を描いたときの中心角の大きさを、1[rad]としています。度[°]との関係は、次のようになります。
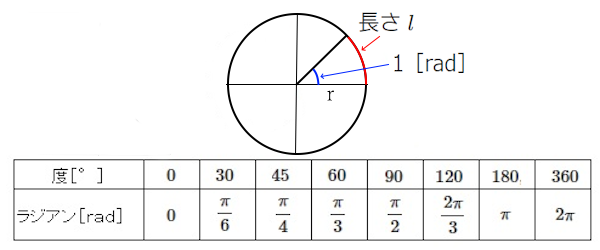
正弦波交流を円運動と考えると周波数が $f$[Hz]のとき、1秒間に $f$ 回転すると考えることができます。1回転の角度は $2π$[rad]ですので、周波数 $f$ と、角速度 $ω$ の関係は次のようになります。
周波数と角速度の関係
$ω=2πf$
$ω$[rad/s]:角速度
$f$[Hz]:周波数
角速度 の基本的な公式は $ω=2πf$ ですが、他にも公式がいくつかあります。関連の物理公式も含めて、覚えておきましょう。
周期と角速度の関係
$ω=\displaystyle \frac{2π }{ T }$
$ω$[rad/s]:角速度
$T$[Hz]:周期
速度と角速度の関係
$ω=\displaystyle \frac{ v }{ r }$
$ω$[rad/s]:角速度
$v$[m/s]:速度
$r$[m]:円の半径
回転角を求める公式
$θ=ωt$
$θ$[rad]:回転角
$ω$[rad/s]:角速度
$t$[秒]:時間
瞬時値と最大値
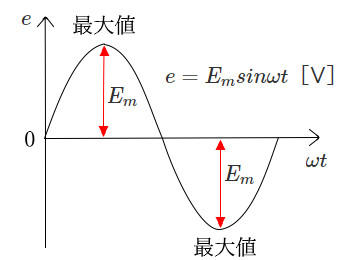
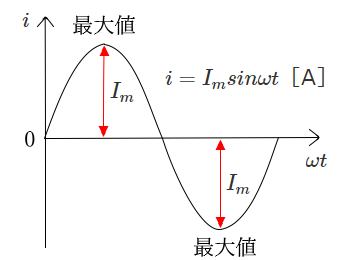
正弦波交流の起電力 $e$ と電流 $i$ は次の式で表します。
$e=E_msinωt$[V]
$i=I_msinωt$[A]
起電力 $e$ と電流 $i$ は「瞬時値」を表し、そのときどきの値です。$E_m$ と $I_m$ は「最大値」を表し、正弦波交流の波形が最も高くなる(低くなる)ときの値です。尚、一般的に瞬時値は $e$ や $i$ のように小文字で、最大値は $E_m$ や $I_m$ のように大文字で表します。
正弦波交流の電圧式
$e=E_msinωt$[V]
$e$[V]:電圧の瞬時値
$E_m$[V]:電圧波形の最大値
$ωt$:角度
正弦波交流の電流式
$i=I_msinωt$[A]
$i$[A]:電流の瞬時値
$I_m$[A]:電流波形の最大値
$ωt$:角度
位相差
複数の正弦波交流の波形がある場合、これらの時間的、角度的なずれのことを「位相差」と言います。
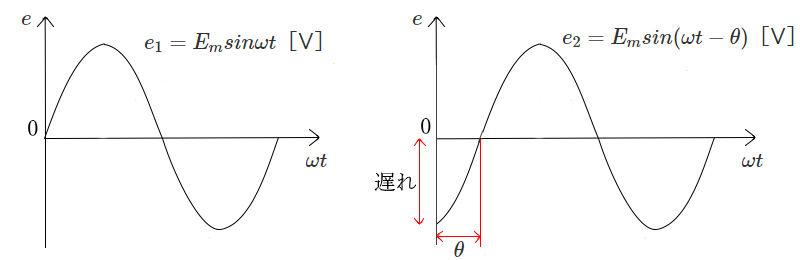
周期が同じ2つの波形 $e_1$,$e_2$ が、図aのようにずれているとき、「 $e_2$ は $e_1$ より位相が遅れている」といいます。
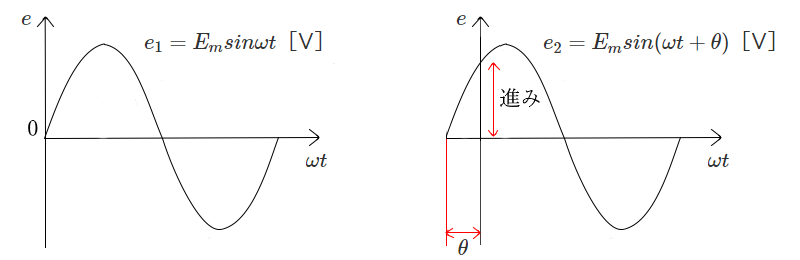
また、波形 $e_1$,$e_2$ が、図bのようにずれているとき、「 $e_2$ は $e_1$ より位相が進んでいる」といいます。
このような、位相のずれの度合いを「位相差 $θ$ 」といい、角度によって表します。位相差 $θ$ は、 $t=0$ を基準にして、遅れていれば負の値、進んでいれば正の値になります。位相差を含めた起電力 $e$ と電流 $i$ の瞬時値は、次の式で表します。
位相差を含めた正弦波交流の電圧式と電流式
$e=E_msin(ωt+θ)$[V]
$e$[V]:電圧の瞬時値
$E_m$[V]:電圧波形の最大値
$ωt$:角度
$θ$:位相差
$i=I_msin(ωt+θ)$[A]
$i$[A]:電流の瞬時値
$I_m$[A]:電流波形の最大値
$ωt$:角度
$θ$:位相差
同相・同位相
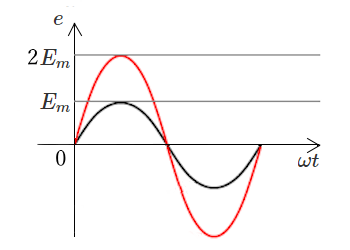
図の2つの波形は、最大値は異なりますが、位相は同じ波形です。このように最大値は違っても、位相が同じ波形のことを「同相」または「同位相」といいます。
同相波形の合成
同相の波形を合成する場合は、最大値の和を求めれば合成することができます。
$e=100\sqrt{2}sin(ωt+θ)$[V]
$e=200\sqrt{2}sin(ωt+θ)$[V]
を合成します。最大値の和は、
$100\sqrt{2}+200\sqrt{2}=300\sqrt{2}$
したがって、合成波形の式は、
$e=300\sqrt{2}sin(ωt+θ)$[V]
となります。
平均値
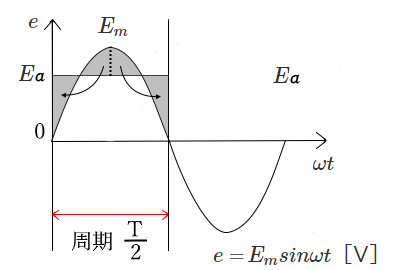
交流波形の瞬時値を時間に対して平均した値を「平均値」といいます。平均値は波形 1 周期分をとると $0$ になりますので、半周期分をとります。
図のように周期 $\displaystyle \frac{ T }{2 }$ の交流起電力の平均値を $E_a$ とすると、平均値 $E_a$ は、長方形 $abcd$ の面積と等しくなります。正弦波交流の起電力 $e$ の平均値を $E_a$ と最大値 $E_m$ の関係は次の式で表すことができます。
交流電圧と電流の平均値
$E_a=\displaystyle \frac{ 2 }{π }E_m$
$E_a$[V]:交流電圧の平均値
$E_m$[V]:電圧波形の最大値
$I_a=\displaystyle \frac{ 2 }{π }I_m$
$I_a$[A]:交流電流の平均値
$I_m$[A]:電流波形の最大値
実効値
交流の電圧や電流は絶えず変化しているため、瞬時値や最大値では、その働きを判断することが難しいです。そのため、交流電力と同じになる直流電力の値で、交流の大きさを表します。この大きさを表す値を「実効値」といいます。一般的に交流の大きさは実効値で表します。家庭用コンセントは実効値が $100$[V]の交流電圧です。
直流回路と交流回路の消費電力[W]は、それぞれ次の式で求めることができます。
直流の消費電力:$P=I^2R$[W]
交流の消費電力:$p=$1周期分の $i^2$ の平均$×R$[W]
交流電力の実効値を $I$ とすると、
$I=\sqrt{1周期分の i^2 の平均 } $[A]
定積分に関する平均値の定理より、
$I=\sqrt{\displaystyle \frac{ 1 }{T }\int_0^T i^2 dx } $[A]
途中の計算式は積分の知識が必要ですので省略しますが、実効値 $I$ と最大値 $I_m$ の関係は、次の式で表すことができます。
$I=\displaystyle \frac{ I_m }{\sqrt{2} }$
また、電圧についても同様に考えることができます。
正弦波交流の起電力の実効値を $E$ とすると、最大値 $E_m$ の関係は次の式で表します。
$E=\displaystyle \frac{ E_m }{\sqrt{2} }$
交流電圧と電流の実効値
$E=\displaystyle \frac{ E_m }{\sqrt{2} }$
$E$[V]:交流電圧の実効値
$E_m$[V]:電圧波形の最大値
$I=\displaystyle \frac{ I_m }{\sqrt{2} }$
$I$[A]:交流電流の実効値
$I_m$[A]:電流波形の最大値
以上より、正弦波交流の起電力 $e$ と電流 $i$ を実効値を使って表すと次の式になります。
正弦波交流の電圧式と電流式
$e=\sqrt{2}Esin(ωt+θ)$[V]
$e$[V]:電圧の瞬時値
$E$[V]:交流電圧の実効値
$ωt$:角度
$θ$:位相差
$i=\sqrt{2}Isin(ωt+θ)$[V]
$i$[A]:電流の瞬時値
$I$[A]:交流電流の実効値
$ωt$:角度
$θ$:位相差
波形率と波高率
波形率と波高率は次のように定義されています。
$波形率=\displaystyle\frac{ 実効値 }{ 平均値 }$
$波高率=\displaystyle\frac{ 最大値 }{ 実効値 }$
「波形率」は、平均値と実効値の割合を表し、「波高率」は、最大値と実効値の割合を表しています。正弦波では電圧あるいは電流の最大値を $Y_m$ とすると、波形率と波高率は次の値になります。
正弦波交流の波形率と波高率
$波形率=\displaystyle\frac{\displaystyle\frac {1}{\sqrt{2}}Y_m}{\displaystyle\frac {2}{π}Y_m}≒1.111$
$波高率=\displaystyle\frac{Y_m}{\displaystyle\frac {1}{\sqrt{2}}Y_m}≒1.414$
正弦波交流のフェーザ形式
正弦波交流の起電力 $e$ や電流 $i$ は、図のように角速度 $ω$ で回転するベクトルと考えることができます。また、位相のずれをベクトルの偏角 $θ$ で表すことができます。
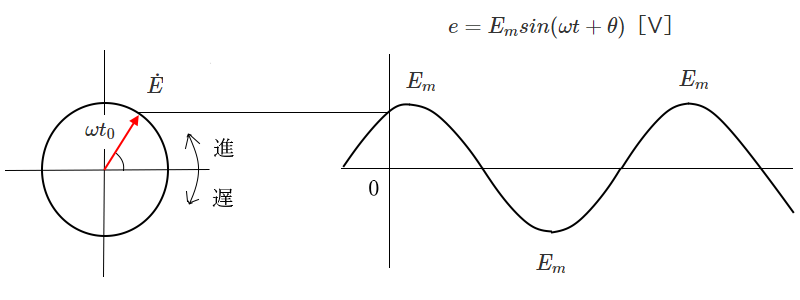
回転ベクトルである交流起電力 $e$ や $i$ の大きさは、静止ベクトル $\dot{E}$ や $\dot{I}$ でも表すことができます。ベクトルの大きさ(絶対値)は正弦波交流の実効値を使います。正弦波交流の起電力 $e$ と電流 $i$ を静止ベクトルで表すと次のようになります。
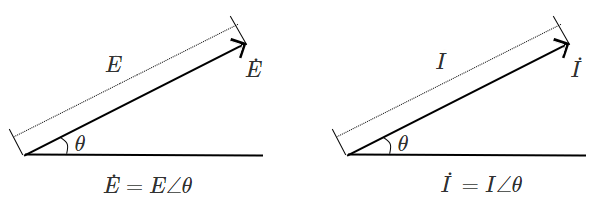
正弦波交流のフェーザ形式
$e=\sqrt{2}Esin(ωt+θ)$ ⇒ $\dot{E}=E∠θ$
$i=\sqrt{2}Isin(ωt+θ)$ ⇒ $\dot{I}=I∠θ$
交流電圧や電流の合成
交流をフェーザ形式で表すと、複数の交流起電力や電流の和を作図的に求めることができます。例として、以下の2つの正弦波交流起電力の和を求めます。
$e_1=10\sqrt{2}sin(ωt)$
$e_2=10\sqrt{2}sin(ωt+\displaystyle \frac{ π }{3})$
2つの正弦波交流起電力をフェーザ形式で表すと次のようになります。
$e_1=10\sqrt{2}sin(ωt)$ ⇒ $\dot{E_1}=10∠0$
$e_2=10\sqrt{2}sin(ωt+\displaystyle \frac{ π }{3})$ ⇒ $\dot{E_2}=10∠\displaystyle \frac{ π }{3}$
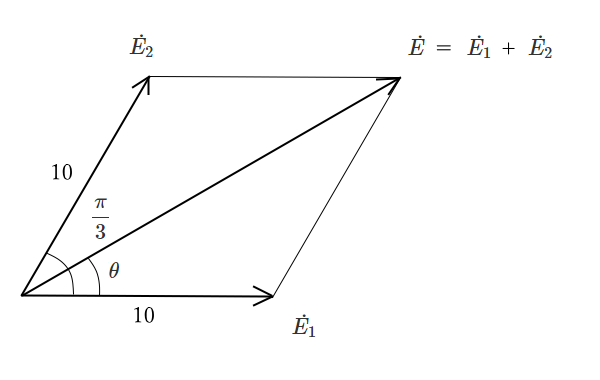
$\dot{E_1}$ と $\dot{E_2}$ のベクトルの和 $\dot{E}=\dot{E_1}+\dot{E_2}$ は、次の図のように平行四辺形の対角線に等しくなります。ベクトル図をもとに、合成起電力の実効値 $E$ と偏角 $θ$ を求めます。
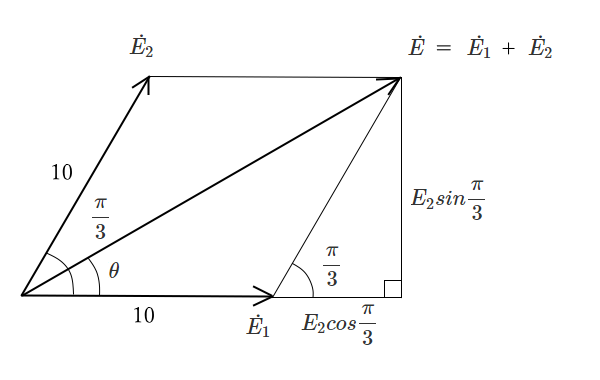
$\begin{eqnarray}|E|&=&\displaystyle\sqrt{(E_1+E_2cos\displaystyle \frac{ π }{3})^2+(E_2sin\displaystyle \frac{ π }{3})^2}\\\\&=&\displaystyle\sqrt{(10+10×\displaystyle \frac{ 1 }{2})^2+(10×\displaystyle \frac{ \sqrt{3 }}{2})^2}\\\\&≒&17.32\end{eqnarray}$
$tanθ=\displaystyle \frac{ E_2sin\displaystyle \frac{ π }{3} }{E_1+E_2cos\displaystyle \frac{ π }{3}}=\displaystyle \frac{5\sqrt{3}}{15}=\displaystyle \frac{1}{\sqrt{3}}$
$θ=\displaystyle \frac{ π }{6}$
したがって、合成起電力 $\dot{E}$[V]は、
$\dot{E}=17.32∠\displaystyle \frac{ π }{6}$[V]
瞬時値 $e$[V]に変換すると、
$e=17.32\sqrt{2}sin(ωt+\displaystyle \frac{ π }{6})$[V]
正弦波交流の複素形式
2乗すると、$-1$ になる数を、記号 $j$ で表します。
$j^2=-1$ ($j=\sqrt{-1}$)
この記号 $j$ を虚数単位といいます。また、
$a+jb$(ただし $a,b$ は実数)
で表される数を複素数といいます。複素数 $a+jb$ は、実数である $a$ と、虚数である $jb$ の組み合わせです。そこで、実数部を $x$ 軸に、虚数部を $y$ 軸とすると、複素数 $a+jb$ は、$xy$ 平面上に点として表すことができます。この平面を複素平面(ガウス平面)といます。
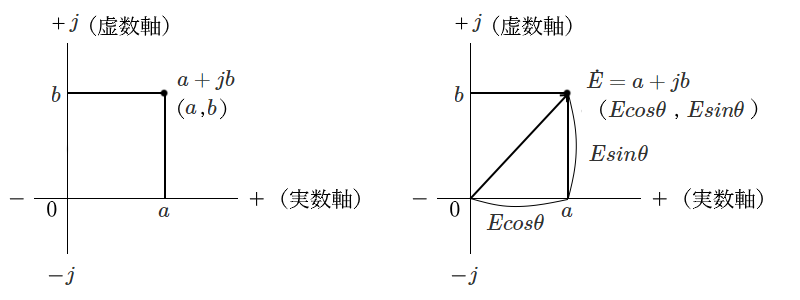
交流起電力を複素平面に当てはめると、実数部 $a$,虚数部 $b$ は、それぞれ $Ecosθ$,$Esinθ$ と、表すことができます。尚、ベクトルの大きさ(絶対値)は正弦波交流の実効値を使います。したがって、
$\dot{E}=a+jb=E(cosθ+jsinθ)$
交流電流も同様に考えることができます。
正弦波交流の複素形式
$\dot{E}=a+jb=E(cosθ+jsinθ)=E∠θ$
$\dot{I}=a+jb=I(cosθ+jsinθ)=I∠θ$
絶対値:$\sqrt{a^2+b^2}$
偏角:$θ=tan^{-1}\displaystyle \frac{ b }{a}$
複素形式による電圧や電流の合成
フェーザ形式と同じ例題を、複素形式で起電力の和を求めてみます。
$e_1=10\sqrt{2}sin(ωt)$
$e_2=10\sqrt{2}sin(ωt+\displaystyle \frac{ π }{3})$
二つの起電力を複素形式に変換します。
$\dot{E_1}=10(cos0+jsin0)=10$
$\begin{eqnarray}\dot{E_2}&=&10(cos\displaystyle \frac{ π }{3}+jsin\displaystyle \frac{ π }{3})\\\\&=&10(\displaystyle \frac{ 1 }{2}+j\displaystyle \frac{ \sqrt{3} }{2})=5+j5\sqrt{3}\end{eqnarray}$
合成起電力を $\dot{E}=\dot{E_1}+\dot{E_2}$ とすると、
$\dot{E}=10+(5+j5\sqrt{3})=15+j5\sqrt{3}$
合成起電力 $\dot{E}$ を変形します。
$|E|=\sqrt{15^2+(5\sqrt{3})^2}=17.32$
$θ=tan^{-1}\displaystyle \frac{ 5\sqrt{3} }{15}=tan^{-1}\displaystyle \frac{ 1 }{\sqrt{3}}=\displaystyle \frac{ π }{6}$
$\dot{E}=17.32(cos\displaystyle \frac{ π }{6}+j\displaystyle \frac{ π }{6})$
瞬時値 $e$[V]に変換すると、
$e=17.32\sqrt{2}sin(ωt+\displaystyle \frac{ π }{6})$[V]
非正弦波交流
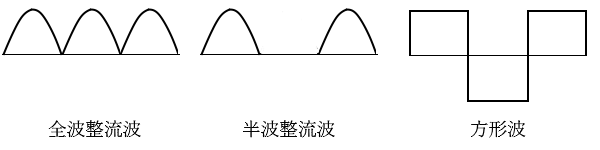
波形が正弦波でない交流のことを「非正弦波交流」といいます。非正弦波交流には「基本波(通常の正弦波交流)」の他に「直流成分」や「高調波」が混ざります。
周波数が $wt$(基本波)の電圧や電流に対して、整数倍の周波数の波形を高調波といいます。3倍の周波数の物を第3高調波、5倍の周波数の物を第5高調波と言います。
奇数倍の高調波が混じることによって、ピーク電圧が高くなります。そのため「絶縁破壊」が起きやすくなるので高調波が問題視されます。
尚、非正弦波交流の実効値を求める式は次のようになります。
非正弦波交流の実効値
$V=\sqrt{{V_0}^2+{V_1}^2+{V_2}^2+{V_3}^2+・・・・}$
$V$:非正弦波交流の実効値(各成分を合成した実効値)
${V_0}^2$:直流成分の実効値
${V_1}^2$:基本波(通常の正弦波交流)の実効値
${V_2}^2$:第2調波の実効値
${V_3}^2$:第3調波の実効値
非正弦波交流の電流の実効値も、同様に求めることができます。
電験三種-理論の過去問解説:正弦波交流の波形
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1997年(平成9年)問6【電験理論の過去問題】
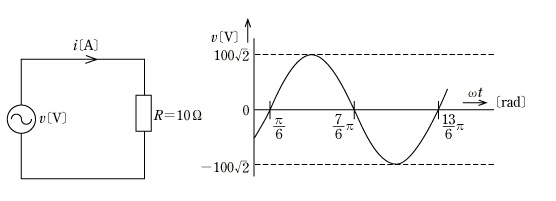
図1の回路において、図2のような波形の正弦波交流電圧 $v$[V]を抵抗 $R=10$[Ω」に加えたとき、流れる電流の瞬時値 $i$[A]を表す式として正しいものは次のうちどれか。ただし、電源の周波数を 50[Hz]とする。
(1) $10sin(50π t-\displaystyle \frac{ π }{ 6 })$
(2) $10sin(50πt+\displaystyle \frac{ π }{ 6 })$
(3) $10sin100πt$
(4) $10\sqrt{ 2 } sin(100π t+\displaystyle \frac{ π }{ 6 })$
(5) $10\sqrt{ 2 }sin (100π t-\displaystyle \frac{ π }{ 6 })$
交流の瞬時値の電流を $i$[A]とすると、
$i=I_msinωt$[A]
電源の周波数は 50[Hz]なので、$ω=2πf$[rad/s]より、
$ω=2πf=100π$
電流の最大値 $I_m$[A]は、
$I_m=\displaystyle \frac{ E_m }{ R }=\displaystyle \frac{ 100\sqrt{2} }{ 10 }=10\sqrt{2}$[A]
この回路に加えた電圧は、0 を基準に見ると $\displaystyle \frac{ π }{ 6 }$ 遅れていますから、位相差は $-\displaystyle \frac{ π }{ 6 }$ になります。
以上を交流の瞬時値の電流 $i$[A]に代入すると、
$i=10\sqrt{2}sin (100π t-\displaystyle \frac{ π }{ 6 })$[A]
答え (5)
1998年(平成10年)問9【電験理論の過去問題】
$v=200sinωt+40sin3ωt+30sin5ωt$[V]で表されるひずみ波交流電圧の波形のひずみ率の値として、正しいのは次のうちどれか。ただし、ひずみ率は次の式による。
$ひずみ率=\displaystyle \frac{ 高調波の実効値[V] }{基本波の実効値[V]}$
(1) 0.05 (2) 0.1 (3) 0.15 (4) 0.2 (5) 0.25
基本波の実効値を $V$[V]、高調波の実効値を $V_n$[V]とすると、
$V=\displaystyle \frac{ 200}{\sqrt{2}}$[V]
$V_n=\sqrt{\displaystyle \left(\frac{ 40}{\sqrt{2}}\right)^2+\displaystyle \left(\frac{ 30}{\sqrt{2}}\right)^2}=\displaystyle \frac{ 50}{\sqrt{2}}$[V]
したがって、ひずみ率は
$ひずみ率=\displaystyle \frac{ \displaystyle \frac{ 50}{\sqrt{2}} }{\displaystyle \frac{ 200}{\sqrt{2}}}=0.25$
答え (5)

正弦波形と違う波形をひずみ波といい、このような波形の交流電圧・電流をひずみ波交流といいます。特に周波数が $wt$(基本波)の電圧や電流に対して、整数倍の周波数の波形を高調波と言います。3倍の周波数の物を第3高調波、5倍の周波数の物を第5高調波と言います。
奇数倍の高調波が混じることによって、ピーク電圧が高くなります。そのため「絶縁破壊」が起きやすくなるので「高調波」が問題視されます。
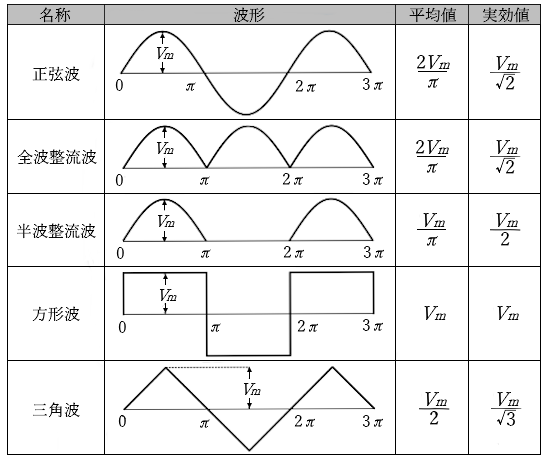
2000年(平成12年)問5【電験理論の過去問題】
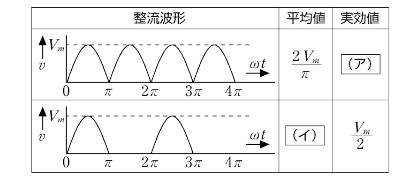
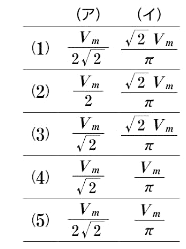
表は、正弦波交流電圧 $v$[V]を全波整流及び半波整流した場合の整流波形について、それぞれの平均値[V]及び実効値[V]を示したものである。表中の空白箇所(ア)及び(イ)に記入する式として、正しいのものを組み合わせたものは次のうちどれか。
交流電圧の実効値を $V$ とすると、$V=\sqrt{1周期分の v^2 の平均 } $[V]です。
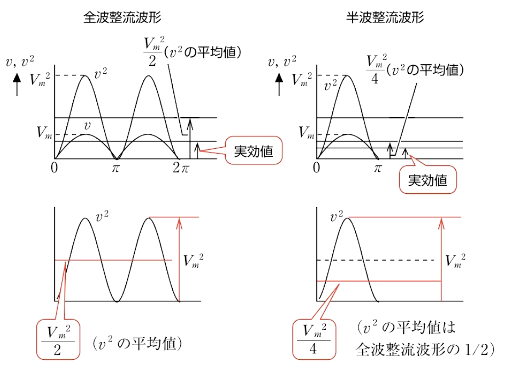
全波整流波形の実効値 $V=\sqrt{\displaystyle \frac{V_m^2}{2} } =\displaystyle \frac{V_m}{\sqrt{2} }$[V]
交流波形の瞬時値を時間に対して平均した値を平均値といいます。半波整流波形の平均値 $V_a$[V]は、半波整流波形の半分になります。
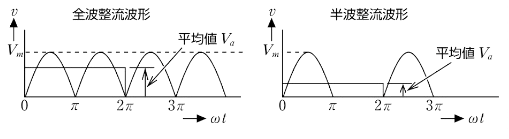
半波整流波形の平均値 $V_a=\displaystyle \frac{V_m}{π}$[V]
答え (4)
2005年(平成17年)問6【電験理論の過去問題】
ある回路に電圧 $v=100sin(100πt+\displaystyle \frac{ π }{ 3 })$[V]を加えたところ、回路に $i=2sin(100πt+\displaystyle \frac{ π }{ 4 })$[A]の電流が流れた。この電圧と電流の位相差 $θ$[rad]を時間[s]の単位に変換して表した値として、正しいのは次のうちどれか。
(1) $\displaystyle \frac{ 1 }{ 400 }$ (2) $\displaystyle \frac{ 1 }{ 600 }$ (3) $\displaystyle \frac{ 1 }{ 1200 }$ (4) $\displaystyle \frac{ 1 }{ 1440 }$ (5) $\displaystyle \frac{ 1 }{ 2400 }$
電圧と電流の位相差 $θ$[rad]は、
$θ=\displaystyle \frac{ π }{ 3 }-\displaystyle \frac{ π }{ 4 }=\displaystyle \frac{ π }{ 12}$[rad]
角速度 $ω=100π$ なので、時間差を $T$[s]とすると、
$θ=ωT$
$\displaystyle \frac{ π }{ 12}=100πT$
$T=\displaystyle \frac{ 1 }{ 1200}$[s]
答え (3)
2006年(平成18年)問8【電験理論の過去問題】
図のように、二つの正弦波交流電圧源 $e_1$[V],$e_2$[V]が直列に接続されている回路 において、合成電圧 $v$[V]の最大値は $e_1$ の最大値の( ア )倍となり、その位相は $e_1$ を基準として( イ )[rad]の( ウ )となる。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句、式または数値と して、正しいものを組み合わせたものは次のうちどれか。


二つの正弦波交流電圧源 $e_1$[V],$e_2$[V]の相関がわかればいいので、$θ$ を除いた状態で考えます。 $e_1$[V],$e_2$[V]は次のようになります。
$e_1=Esin(ωt)$[V]
⇒ $\dot{E_1}=E(cos0+jsin0)=E$
$e_2=\sqrt{3}Esin(ωt+\displaystyle \frac{ π }{ 2})$[V]
⇒ $\dot{E_2}=E(cos\displaystyle \frac{ π }{ 2}+jsin\displaystyle \frac{ π }{ 2})=j\sqrt{3}E$
合成起電力を $\dot{E}$ とすると、
$\dot{E}=\dot{E_1}+\dot{E_2}=E+j\sqrt{3}E$
$|E|=\sqrt{E^2+(\sqrt{3}E)^2}=2E$(ア)
$θ=tan^{-1}\displaystyle \frac{ \sqrt{3}E }{E}=tan^{-1}\sqrt{3}E =\displaystyle \frac{ π }{3}$(イ)
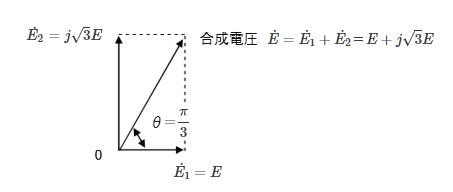
ベクトル図より、合成起電力 $\dot{E}$[V]は 進み(ウ)になります。
答え (5)
2009年(平成21年)問9【電験理論の過去問題】
ある回路に、$ i=4\sqrt{ 2 } sin120πt$[A]の電流が流れている。この電流の瞬時値が、時刻 $t=0$[s]以降に初めて 4[A]となるのは、時刻 $t=t_1$[s]である。$t_1$[s]の値として、正しいのは次のうちどれか。
(1) $\displaystyle \frac{ 1 }{ 480 }$ (2) $\displaystyle \frac{ 1 }{ 360 }$ (3) $\displaystyle \frac{ 1 }{ 240 }$ (4) $\displaystyle \frac{ 1 }{ 160 }$ (5) $\displaystyle \frac{ 1 }{ 120 }$
題意より
$ 4=4\sqrt{ 2 } sin120πt_1$
$ sin120πt_1=\displaystyle \frac{ 1 }{ \sqrt{2} }=sin\displaystyle \frac{π }{ 4 }$
したがって、$t_1=\displaystyle \frac{1 }{ 480 }$[s]
答え (1)
2015年(平成27年)問14【電験理論の過去問題】
目盛が正弦波交流に対する実効値になる整流形の電圧計(全波整流形)がある。この電圧計で図のような周期20msの繰り返し波形電圧を測定した。このとき、電圧計の指示の値 [V] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
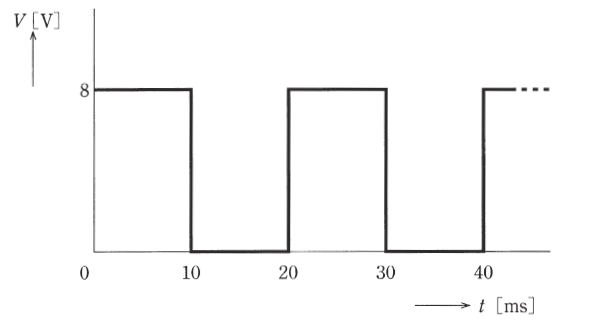
(1) 4.00 (2) 4.44 (3) 4.62 (4) 5.14 (5) 5.66
周期 20 [ms] の間の平均電圧は 4 [V] です。波形率は、
$波形率=\displaystyle\frac{\displaystyle\frac {1}{\sqrt{2}}Y_m}{\displaystyle\frac {2}{π}Y_m}≒1.111$
です。また、 $波形率=\displaystyle\frac{ 実効値 }{ 平均値 }$ より
実効値=4×1.11=4.44 [V]
答え (2)
2017年(平成29年)問9【電験理論の過去問題】
$R=5Ω$ の抵抗に、ひずみ波交流電流
$i = 6sinωt + 2sin3ωt$[A]
が流れた。
このとき、抵抗 $R=5Ω$ で消費される平均電力 $P$ の値[W]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、$ω$ は角周波数[rad/s]、$t$ は時刻[s]とする。
(1) 40 (2) 90 (3) 100 (4) 180 (5) 200
基本波成分の実効値を $I_1$[A]、第3高調波成分の実効値を $I_3$[A]とすると、
$I_1=\displaystyle\frac{6}{\sqrt{2}}=3\sqrt{2}$[A]
$I_3=\displaystyle\frac{2}{\sqrt{2}}=\sqrt{2}$[A]
ひずみ波交流電流の実効値を $I_1$[A]とすると、
$I_1=\sqrt{{I_1}^2+{I_3}^2}=\sqrt{(3\sqrt{2})^2+(\sqrt{2})^2}=\sqrt{18+2}=\sqrt{20}$
平均電力 $P$ の値[W]は、
$P=RI^2=5×(\sqrt{20})^2=100$[W]
答え(3)
電験三種の理論科目に出題される「単相交流分野」のページ
1.正弦波交流の波形
2.単相交流の直列回路
3.単相交流の並列回路
4.RLC直列共振回路
5.RLC並列共振回路
6.単相交流の電力と力率
電験三種の理論科目に出題される「三相交流分野」のページ
1.三相交流回路
2.三相交流の電力と力率






