第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「自己インダクタンス」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「自己インダクタンス」の過去問題も解説しています。
磁気回路のオームの法則
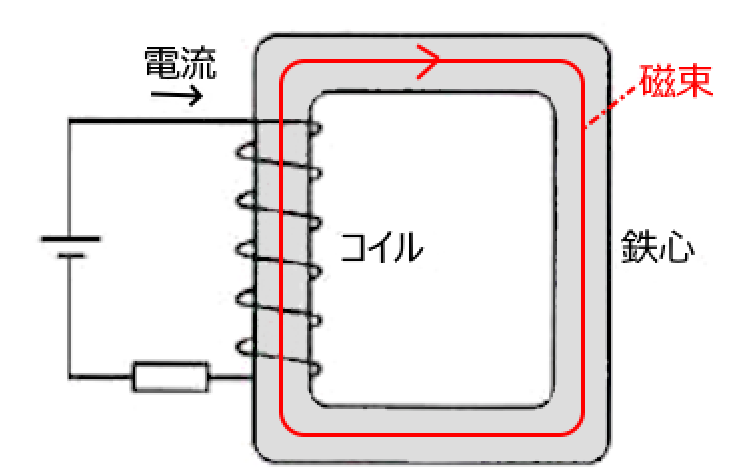
電流の流れる回路を電気回路と呼びますが、同じように磁束の通る回路を磁気回路といいます。図のように鉄心にコイルを巻いてコイルに電流を流すと、鉄心に磁束が発生します。
磁気回路は、コイルの巻き数と流す電流が多いほど、発生する磁束の量が多くなります。コイルの巻き数と流す電流の積 $NI$(単位:アンペア[A])を「起磁力」といいます。
磁気抵抗を求める式①
$R_{ m }=\displaystyle \frac{ NI}{ ϕ }$[A/WbまたはH-1]
$R_m$[A/WbまたはH-1]:磁気抵抗
$N$ :コイルの巻数
$I$[A]:コイルに流れる電流
$ϕ$[Wb]:磁束
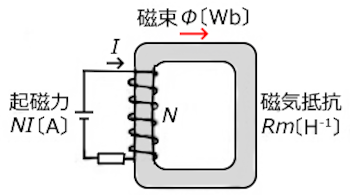
起磁力 $NI$ は、$F_m$ と表現することもあります。
磁気回路を通る磁束は、磁路の長さ $l$[m]が長いほど通りにくく、断面積 $S$[m2]が小さいほど通りにくくなります。この磁束を妨げる要因を磁気抵抗 $R_{ m }$[A/WbまたはH-1]で表します。電気回路の抵抗と同じ考えかたです。
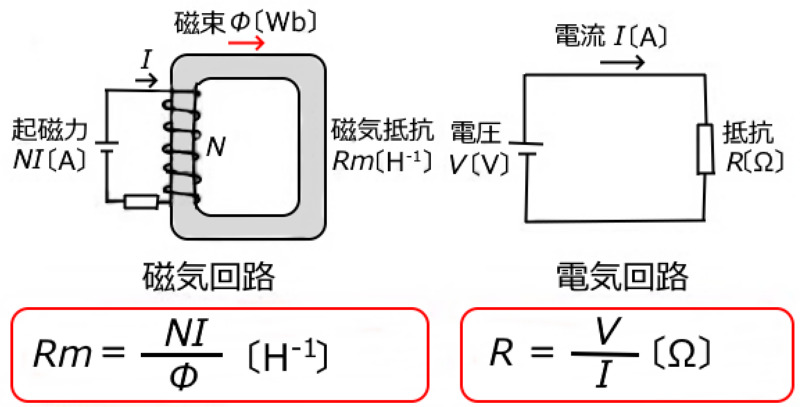
磁気抵抗を求める式②
$R_{ m }=\displaystyle \frac{ l}{ μS}$[A/WbまたはH-1]
$R_m$[A/WbまたはH-1]:磁気抵抗
$l$[m]:環状鉄心の長さ
$S$[m2]:環状鉄心の断面積
$μ$:環状鉄心の透磁率
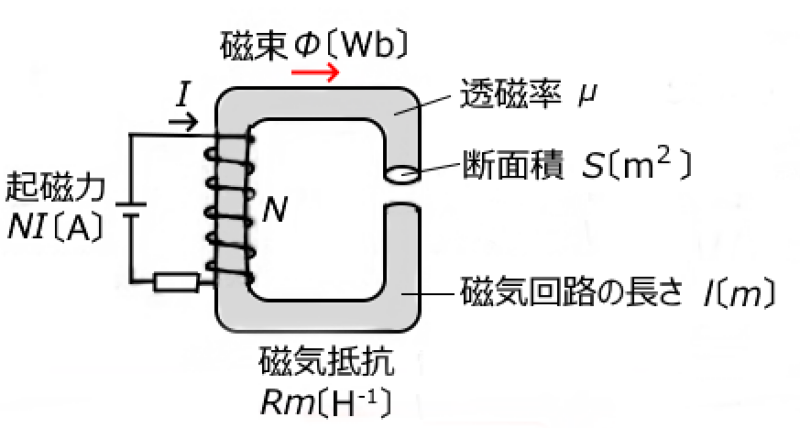
磁気抵抗の大きさ $R_{ m }$[A/WbまたはH-1]は、磁束を通す物質の長さ $l$[m]に比例し、その断面積 $S$[m2]に反比例します。
自己誘導作用と自己インダクタンス
自己誘導作用
磁気回路では、電流の増減に伴って磁場の強さが変化し、その磁場の変化による電磁誘導が発生し、電流の変化を妨げる方向に誘導起電力(逆起電力)が発生します。これを「自己誘導」といいます。
レンツの法則は電磁誘導によって発生する起電力は、磁束の変化を妨げる電流を生じるような方向に発生するという法則です。コイルは磁石が近づいてくると反発し、遠ざかると引き付ける方向です。
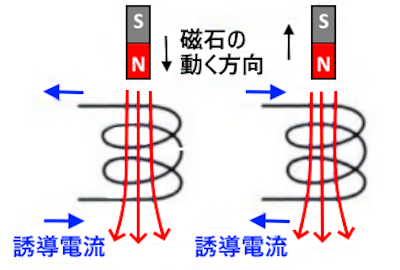
コイルにN極を近づけると、コイルを貫く下向きの磁束が増加します。このとき誘導電流による磁界が上向きになるように誘導電流が流れます。
N極をコイルから遠ざけると、コイルを貫く下向きの磁束が減少します。このとき誘導電流による磁界が下向きになるように誘導電流が流れます。
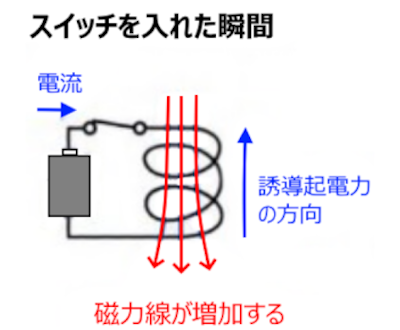
スイッチを入れた瞬間、電流が大きくなります。コイル内の磁界は大きくなり、電磁誘導が起こります。レンツの法則により、流れている電流と反対方向に誘導起電力が発生し、電流の増加を妨害します。
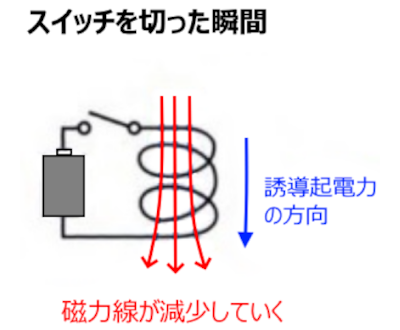
スイッチを切った瞬間、電流が小さくなります。コイル内の磁場は小さくなり、電磁誘導が起こります。レンツの法則により、流れている電流と同じ方向に誘導起電力が発生し、電流の減少を妨害します。
この妨害は一瞬のうちに終了します。磁界の変化はスイッチを入れた瞬間や切った瞬間だけ起こります。磁界の変化が小さくなるにつれて誘導起電力も小さくなります。磁界の変化は、短時間で 0 になり、妨害もおさまります。
自己インダクタンス
ファラデーの電磁誘導の法則より、時間 $Δt $[s]の間に コイルを貫く磁束が $Δϕ$[Wb]だけ変化するとき、$N$ 巻きのコイルに発生する誘導起電力 $e$[V]は、次のように表されます。
$e=-N\displaystyle\frac{Δϕ}{Δt}$
磁気回路のオームの法則は次のように表されます。
$R_{ m }=\displaystyle \frac{ NI}{ ϕ }=\displaystyle \frac{ l}{ μS}$
$ ϕ =\displaystyle\frac{μSNI}{l }$
この式をファラデーの法則に代入すると、磁束の変化は電流の変化と比例するので電流変化分を $ΔI$とすれば、
$e=-N\displaystyle\frac{1}{Δt}×\displaystyle\frac{μSNΔI}{l }=-\displaystyle\frac{μSN^2}{l}\frac{ΔI}{Δt}$
この $\displaystyle\frac{μSN^2}{l}$ を「自己インダクタンス」いい、記号 $L$(単位 ヘンリー[H])で表します。
$L=\displaystyle\frac{μSN^2}{l}$
自己誘導による誘導起電力の公式
巻数 $N$、自己インダクタンス $L$[H]のコイルに流す電流を $Δt $[s]間に $ΔI $[A]だけ変化させると、コイルの磁束は $Δ ϕ $[Wb]だけ変化します。このとき、誘導起電力 $e$[V] は、次のように表されます。
$e=-L\displaystyle\frac{ΔI}{Δt}$
$e$[V]:コイルに発生する誘導起電力
$L$[H]:自己インダクタンス
$ΔI$[A]:変化した電流の量
$Δt$[s]:電流が変化するのに要した時間
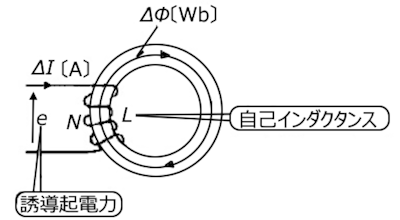
ファラデーの法則より
$e=-N\displaystyle\frac{Δϕ}{Δt}=-L\frac{ΔI}{Δt}$
$L=N\displaystyle\frac{Δϕ}{ΔI}$
と表わすこともできます。
磁束鎖交数
コイルの巻数 $N$ と 磁束 $ ϕ $ との積 $N ϕ $ を「磁束鎖交数」 $ Ψ$(プシー又はプサイ)といいます。$N$巻のコイルに $I$[A]の電流を流したとき、磁束が $ ϕ $[Wb]生じたときの磁束鎖交数 $Ψ$は、次の式で表すことができます。
磁束鎖交数 $Ψ$ を求める公式
$Ψ=N ϕ =LI$[Wb]
$Ψ$[Wb]:磁束鎖交数
$L$[H]:自己インダクタンス
$φ$[Wb]:磁束
$N$:コイルの巻数
$I$[A]:コイルに流れる電流
電験三種-理論の過去問解説:自己インダクタンス
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1998年(平成10年)問2【電験理論の過去問題】
磁気回路における磁気抵抗に関する記述のうち、誤っているのはどれか。
| (1) | 磁気抵抗は、次の式で表される。 $磁気抵抗=\displaystyle\frac{起磁力}{磁束}$ |
| (2) | 磁気抵抗は、磁路の断面積に比例する。 |
| (3) | 磁気抵抗は、比透磁率に反比例する。 |
| (4) | 磁気抵抗は、磁路の長さに比例する。 |
| (5) | 磁気抵抗の単位は、[$H^{-1}$]である。 |
起磁力 $NI$[A]、磁束を妨げる要因である磁気抵抗 $R_{ m }$[A/Wbまたは$H^{-1}$]、磁束 $ ϕ $[Wb]の関係は次式で表されます。
$R_{ m }=\displaystyle \frac{ NI}{ ϕ }$
磁気抵抗の大きさ $R_{ m }$[A/Wbまたは$H^{-1}$]は、磁束を通す物質の長さ $l$[m]に比例し、その断面積 $S$[m2]に反比例します。
以上より(2)の記述が間違いです。
答え (2)
2002年(平成14年)問3【電験理論の過去問題】
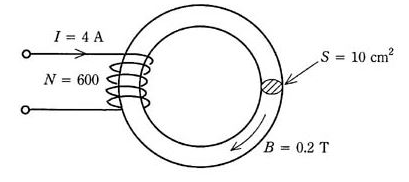
図のように、断面積 $S=10$[cm2]の環状鉄心に巻かれた巻数 $N=600$ のコイルがある。このコイルに直流電流 $I=4$[A]を流したとき、鉄心中に発生した磁束の磁束密度は $B=0.2$[T]であった。このコイルのインダクタンス $L$[mH]の値として、正しいのは次のうちどれか。
ただし、コイルの漏れ磁束は無視できるものとする。
(1) 30 (2) 60 (3) 120 (4) 300 (5) 600
自己インダクタンスは $L=N\displaystyle\frac{Δ ϕ }{ΔI}$[H]、磁束 $ ϕ =BS$[Wb]より
$\begin{eqnarray}L&=&N\displaystyle\frac{Δ ϕ }{ΔI}\\\\&=&N\displaystyle\frac{ΔBS}{ΔI}\\\\&=&600×\displaystyle\frac{0.2×10×10^{-4}}{4}\\\\&=&0.03=30[mH]\end{eqnarray}$
答え (1)
2004年(平成16年)問15【電験理論の過去問題】
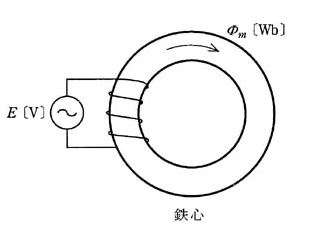
図のような環状コイルがある。交流電圧の実効値を $E$[V]、交流電圧の周波数を $f$[Hz]としたとき、鉄心中の最大磁束は $ ϕ _m$[Wb]であった。次の(a)及び(b)に答えよ。
ただし、鉄心の飽和はなく、漏れ磁束もないものとする。
(a) 電源の周波数 $f$[Hz]一定で、電圧を $1.5E$[V]にしたとき、最大磁束[Wb]は、$ ϕ _m$[Wb]の何倍になるか。その倍率として、最も近いものは次のうちどれか。
(1) 0.67 (2) 0.16 (3) 1.5 (4) 2.25 (5) 4.0
(b) 電圧を $1.5E$[V]にして、周波数を $0.5f$[Hz]にしたとき、最大磁束[Wb]は $ ϕ _m$[Wb]の何倍になるか。その倍率として、最も近いものは次のうちどれか。
(1) 0.33 (2) 0.75 (3) 1.33 (4) 2.25 (5) 3.0
(a) この問題は、交流回路の誘導性リアクタンスについての知識が必要です。
誘導性リアクタンスは $X_L=2πfL $[Ω]で表され、電圧、電流、誘導性リアクタンスの関係は $E=X_LI$ の関係があります。
題意より、周波数 $f$ が一定ですので、$E$ が1.5倍になると $I$ も1.5倍になります。磁束は $ ϕ =\displaystyle\frac{μSNI}{l }$ で表すことができますので、$I$ が1.5倍になると最大磁束 $ ϕ _m$ も1.5倍になります。
答え (3)
(b) 周波数 $f$ を0.5倍にすると、誘導性リアクタンスは $X’_L$[Ω]は
$X_L=2π×0.5fL =0.5X_L$[Ω]
となります。電圧を $1.5E$ [V]にしたとき流れる電流 $I’ $[A]は $E=X_LI$ より、
$I’=\displaystyle\frac{1.5E}{0.5X’_L }=3I$
となり流れる電流は3倍になり、最大磁束 $ ϕ _m$ も3倍になります。
答え (5)
2006年(平成18年)問4【電験理論の過去問題】
巻数 $N=10$ のコイルを流れる電流が 0.1秒間に 0.6[A]の割合で変化しているとき、コイルを貫く磁束が 0.4秒間に 1.2[mWb]の割合で変化した。このコイルの自己インダクタンス $L$[mH]の値として、正しいのは次のうちどれか。
ただし、コイルの漏れ磁束は無視できるものとする。
(1) 0.5 (2) 2.5 (3) 5 (4) 10 (5) 20
自己インダクタンスは $L=N\displaystyle\frac{Δ ϕ }{ΔI}$で表されます。
$ΔI=\displaystyle\frac{0.6}{0.1}=6$
$Δ ϕ =\displaystyle\frac{1.2×10^{-3}}{0.4}=3×10^{-3}$
$L=10×\displaystyle\frac{3×10^{-3}}{6}=5×10^{-3}=5$[mH]
答え (3)
2008年(平成20年)問3【電験理論の過去問題】
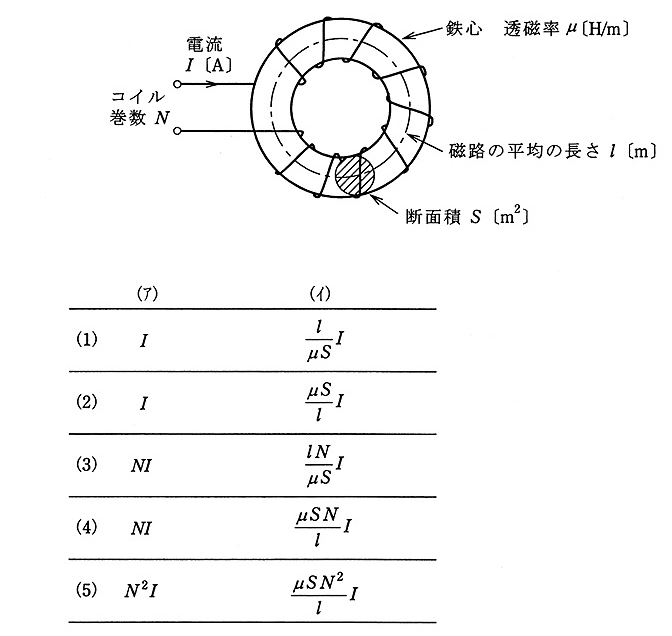
図のように、磁路の平均の長さ $l$[m]、断面積 $S$[㎡]で透磁率 $μ$[H/m]の環状鉄心に巻数 $N$ のコイルが巻かれている。この場合、環状鉄心の磁気抵抗は $\displaystyle\frac{l}{μS}$[A/Wb]である。いま、コイルに流れている電流を $I$[A]としたとき、起磁力は( ア )であり、したがって、磁束は( イ )[Wb]となる。
ただし、鉄心及びコイルの漏れ磁束はないものとする。
上記の記述中の空白箇所(ア)及び(イ)に当てはまる式として、正しいものを組み合わせたのは次のうちどれか。
コイルの巻き数と流す電流の積 $NI$(単位 アンペア:[A])を起磁力といいます。
起磁力$NI$[A]、磁束を妨げる要因である磁気抵抗 $R_{ m }$[A/Wbまたは$H^{-1}$]、磁束 $ ϕ $[Wb]の関係は次式で表されます。
$R_{ m }=\displaystyle \frac{ NI}{ ϕ }$
磁気抵抗の大きさ$R_{ m }$[A/Wbまたは$H^{-1}$]は、磁束を通す物質の長さ $l$[m]に比例し、その断面積 $S$[m2]に反比例します。
$R_{ m }=\displaystyle \frac{ l}{ μS}$
したがって
$\displaystyle \frac{ NI}{ ϕ }=\displaystyle \frac{ l}{ μS}$
$ ϕ =\displaystyle \frac{μNS }{ l}I$
答え (4)
2014年(平成26年)問3【電験理論の過去問題】
環状鉄心に絶縁電線を巻いて作った磁気回路に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- 磁気抵抗は、磁束の通りにくさを表している。毎へンリー[$H^{-1}$]は、磁気抵抗の単位である。
- 電気抵抗が導体断面積に反比例するように、磁気抵抗は、鉄心断面積に反比例する。
- 鉄心の透磁率が大きいほど、磁気抵抗は小さくなる。
- 起磁力が同じ場合、鉄心の磁気抵抗が大きいほど、鉄心を通る磁束は小さくなる。
- 磁気回路における起磁力と磁気抵抗は、電気回路におけるオームの法則の電流と電気抵抗にそれぞれ対応する。
起磁力$NI$[A]、磁束を妨げる要因である磁気抵抗 $R_{ m }$[A/Wbまたは$H^{-1}$]、磁束 $ ϕ $[Wb]の関係は次式で表されます。
$R_{ m }=\displaystyle \frac{ NI}{ ϕ }$
磁気抵抗の大きさ$R_{ m }$[A/Wbまたは$H^{-1}$]は、磁束を通す物質の長さ $l$[m]に比例し、その断面積 $S$[m2]に反比例します。
$R_{ m }=\displaystyle \frac{ l}{ μS}$
したがって、(5)の記述中で磁気回路における起磁力は、電気回路におけるオームの法則の電圧にそれぞれ対応しているので誤りです。
答え (5)
電験三種の理論科目に出題される「電磁気分野」のページ
1.磁力線と磁束
2.アンペールの法則
3.フレミングの左手の法則
4.電流が磁界から受ける力
5.ヒステリシス曲線と損失
6.電磁誘導(レンツの法則とファラデーの法則)
7.自己インダクタンス
8.相互インダクタンス
9.磁気エネルギー






