このページでは、短絡容量と短絡電流の計算について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の電力科目の試験で、実際に出題された短絡容量と短絡電流の計算の過去問題も解説しています。
- 定格遮断容量と短絡容量
- 百分率インピーダンス法と短絡電流
- 三相交流の百分率インピーダンス
- 三相短絡電流の計算手順
- 中性線接地方式の一線地絡電流
- 電験三種-電力(変電所)過去問題
- 1998年(平成10年)問12
- 1998年(平成10年)問12 過去問解説
- 2002年(平成14年)問12
- 2002年(平成14年)問12 過去問解説
- 2003年(平成15年)問10
- 2003年(平成15年)問10 過去問解説
- 2004年(平成16年)問16
- 2004年(平成16年)問16 過去問解説
- 2006年(平成18年)問17
- 2006年(平成18年)問17 過去問解説
- 2007年(平成19年)問12
- 2007年(平成19年)問12 過去問解説
- 2008年(平成20年)問8
- 2008年(平成20年)問8 過去問解説
- 2009年(平成21年)問16
- 2009年(平成21年)問16 過去問解説
- 2011年(平成23年)問16
- 2011年(平成23年)問16 過去問解説
- 2013年(平成25年)問17
- 2013年(平成25年)問17 過去問解説
- 2016年(平成28年)問16
- 2016年(平成28年)問16 過去問解説
定格遮断容量と短絡容量
三相の定格遮断容量
遮断器が定格電圧で遮断できる電流を定格遮断電流といい、開閉できる最大の容量を定格遮断容量といいます。三相の場合は次の式で表すことができます。
三相の定格遮断容量[V・A]
$\sqrt{ 3 } $×定格電圧×定格遮断電流
三相短絡容量
遮断器は三相短絡電流を遮断できる能力が必要です。短絡容量は事故時に遮断器を通る電流によって求めることができます。
三相短絡容量[V・A]
$\sqrt{ 3 } $×系統の線間電圧×三相短絡電流
百分率インピーダンス法と短絡電流
百分率インピーダンス(%Z)は、負荷電流(線電流)In[A]が流れるとき、1相当たりの線路や変圧器内部などのインピーダンス Z[Ω]によって生じる電圧降下 InZ[V]が、相電圧(対地間電圧)En[V]の何パ―セントになるかを表したものです。
百分率インピーダンス(%Z)の定義式
$\%Z=\displaystyle \frac{ I_nZ }{E_n}×100$[%]
%$Z$:百分率インピーダンス
$I_n$[A]:負荷電流
$Z$[Ω]:インピーダンス
$E_n$[V]:相電圧
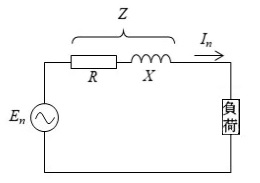
定義式からわかるように、百分率インピーダンスとは、インピーダンスにより発生する「電圧降下」と「相電圧」との比を百分率で表したものです。
例えば、相電圧が 100[V]の回路で、インピーダンスによる電圧降下が 5[V]だったときの百分率インピーダンスは 5% になります。
百分率インピーダンスと短絡電流
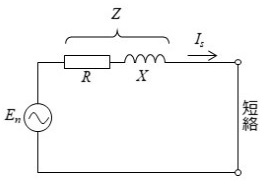
短絡事故とは、電線間が抵抗 0[Ω]で接続された状態になることです。通常の回路では、電源から流れ出た電流は 電線を経由して負荷を通り、また電源へと戻ってくる、という流れになりますが、短絡事故が起きた場合、電源から流れ出た電流は負荷を通らずに 電線だけを流れて電源へと戻ります。そのため短絡時に流れる電流は、とても大きくなります。
その短絡電流を、百分率インピーダンス(%インピーダンス)法で求めてみます。負荷で短絡事故が起こった場合の短絡電流を $I_S$ とします。オームの法則より、$I_S=\displaystyle \frac{ E_n }{Z}$ で求めることができます。この式から Z を %Z で表します。
百分率インピーダンス法による短絡電流を求める式
$I_S = \displaystyle \frac{ E_n }{Z}=\displaystyle \frac{ E_n }{\displaystyle \frac{ \%Z×E_n }{I_n×100}} =I_n×\displaystyle \frac{ 100 }{ \%Z} $
$\%Z=\displaystyle \frac{ I_n }{I_S}×100$
%$Z$:百分率インピーダンス
$I_n$[A]:負荷電流
$I_S$[A]:短絡電流
三相交流の百分率インピーダンス
三相交流は相電圧よりも線間電圧で表す場合が多いので、線間電圧を Vn[V]とすれば、百分率インピーダンス %Z は次の式で表すことができます。
$\%Z=\displaystyle \frac{ \sqrt{ 3 }I_nZ }{V_n}×100$[%]
ここで、定格容量を P[V・A]とすると、$P=\sqrt{ 3 }V_nI_n$ ですので、次の式に変形することができます。
$\begin{eqnarray}\%Z &=& \displaystyle \frac{ \sqrt{ 3 }I_nZ }{V_n}×100 \\\\ &=&\displaystyle \frac{ \sqrt{ 3 }I_nZ ×V_n}{V_n×V_n}×100 \\\\ &=&\displaystyle \frac{ PZ }{V_n^2}×100\end{eqnarray}$
三相短絡電流 IS は、$I_S=\displaystyle \frac{ V_n }{\sqrt{ 3 }Z}$ で求めることができます。この式からインピーダンス Z を %Z で表します。
$I_S = \displaystyle \frac{ V_n }{\sqrt{ 3 }Z}=\displaystyle \frac{ V_n }{\displaystyle \frac{ \sqrt{ 3 }×\%Z×V_n }{\sqrt{ 3 }×I_n×100}} =I_n×\displaystyle \frac{ 100 }{ \%Z} $
三相の百分率インピーダンスと短絡電流の関係式
$\%Z=\displaystyle \frac{ \sqrt{ 3 }I_nZ }{V_n}×100=\displaystyle \frac{ PZ }{V_n^2}×100$[%]
$\%Z=\displaystyle \frac{ I_n }{I_S}×100$
%$Z$:百分率インピーダンス
$I_n$[A]:負荷電流
$Z$[Ω]:インピーダンス
$V_n$[V]:線間電圧
$P$[V・A]:定格容量
$I_S$[A]:短絡電流
三相短絡電流の計算手順
電線路や変圧器には、基準容量 PB と 百分率インピーダンス %Z という要素があります。複数の電線路(変圧器) の百分率インピーダンスを合成することがありますが、基準容量が異なる場合、百分率インピーダンスをそのまま合成することができません。そのため、百分率インピーダンスを、同一の基準容量に換算する必要が出てきます。
計算の手順としては、はじめに基準電圧 VB[V]と基準容量 PB[V・A]を決めます。基準電圧は短絡点の線間電圧とすることが多いです。基準容量は全構成機器の基準となる容量で、任意に設定できます。
ある機器 T の定格容量(自己容量)を PT[V・A]、パーセントインピーダンスを %ZT とすると、基準容量 PB[W]の下でのパーセントインピーダンス %Z’ は、次の式で表すことができます。
$\%Z’_T=\%Z_T×\displaystyle \frac{ P_B }{ P_T}$
次に、短絡点から電源側をみたときの合成パーセントインピーダンス %Z を計算します。そして、次の式で定格電流 In を計算し、三相短絡電流 IS を求めます。
$P_B=\sqrt{ 3 } V_BI_n$
$I_n=\displaystyle \frac{ P_B }{ \sqrt{ 3 } V_B}$
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }$
三相短絡電流の計算手順 例1
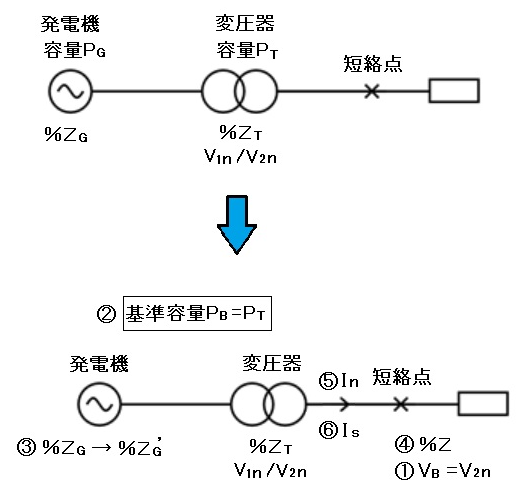
① 短絡点の線間電圧を基準電圧 VB とします。
$V_B=V_{2n}$ (変圧器の定格電圧2次側)
② 基準容量 PB を設定します。(任意に設定できます。)
$P_B=P_T$
③ 各機器の パーセントインピーダンス を基準容量 PB に合わせて換算します。
$\%Z’_G=\%Z_G×\displaystyle \frac{ P_B }{ P_G}$
$\%Z’_T=\%Z_T×\displaystyle \frac{ P_B }{ P_T}=\%Z_T$
④ 短絡点から電源側の合成%インピーダンス( %Z )を計算します。
$\%Z=\%Z’_G+\%Z_T$
⑤ 基準容量 PB と基準電圧 VB から、定格電流 In を計算します。
$P_B=\sqrt{ 3 } V_BI_n=\sqrt{ 3 } V_{2n}I_n$
$I_n=\displaystyle \frac{ P_B }{ \sqrt{ 3 } V_{2n}}$
⑥ 三相短絡電流 IS を計算します。
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }$
三相短絡電流の計算手順 例2
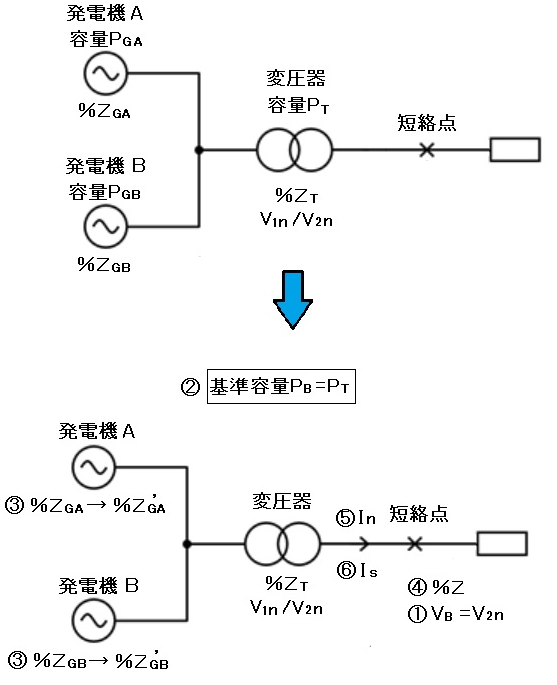
① 短絡点の線間電圧を基準電圧 VB とします。
$V_B=V_{2n}$ (変圧器の定格電圧2次側)
② 基準容量 PB を設定します。(任意に設定できます。)
$P_B=P_T$
③ 各機器の パーセントインピーダンス を基準容量 PB に合わせて換算します。
$\%Z_{GA}’=\%Z_{GA}×\displaystyle \frac{ P_B }{ P_{GA}}$
$\%Z_{GB}’=\%Z_{GB}×\displaystyle \frac{ P_B }{ P_{GB}}$
$\%Z’_T=\%Z_T×\displaystyle \frac{ P_B }{ P_T}=\%Z_T$
④ 短絡点から電源側の合成%インピーダンス( %Z )を計算します。
$\%Z=\displaystyle \frac{ \%Z_{GA}’ \%Z_{GB}’}{\%Z_{GA}’+\%Z_{GB}’}+\%Z_T$
⑤ 基準容量 PB と基準電圧 VBから、定格電流 In を計算します。
$P_B=\sqrt{ 3 } V_BI_n=\sqrt{ 3 } V_{2n}I_n$
$I_n=\displaystyle \frac{ P_B }{ \sqrt{ 3 } V_{2n}}$
⑥ 三相短絡電流 IS を計算します。
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }$
中性線接地方式の一線地絡電流
中性線の接地抵抗が R[Ω]の系統で、一線地絡事故が発生した場合、地絡の抵抗 Rg[Ω]を通して、地絡電流 Ig[A]が流れます。
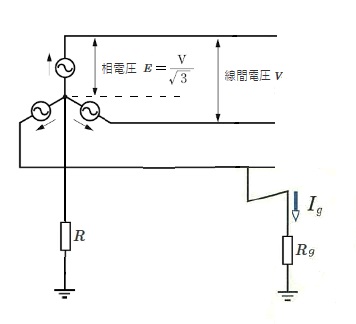
$I_g=\displaystyle \frac{ E }{ R+R_g}$
尚、中性線非接地方式の系統においては、対地静電容量の影響を考慮しなければなりません。
電験三種-電力(変電所)過去問題
1998年(平成10年)問12
図のような送電系統のF点において、三相短絡を生じたとき、F点における短絡電流[A]の値として、正しいのは次のうちどれか。ただし、発電機容量は 10000[kVA]、出力電圧は 11[kV]、リアクタンスは自己容量ベースで 25[%]である。また、変圧器容量は 10000[kVA]、変圧比は 11[kV]/33[kV]、リアクタンスは自己容量ベースで 5[%]、送電線TF間のリアクタンスは 10000[kVA]ベースで 10[%]とする。
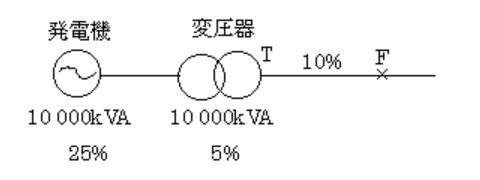
(1) 85 (2) 194 (3) 235 (4) 337 (5) 438
1998年(平成10年)問12 過去問解説
短絡点の線間電圧を基準電圧 VB とします。
$V_B=33$ [kV]
基準容量 PB を設定します。
$P_B=10000$[kVA]
短絡点から電源側の合成%リアクタンス( %X )を計算します。
$\%X=\%X_G+\%X_T+\%X_{TF}=25+5+10=40$
基準容量 PB と基準電圧 VB から、定格電流 In を計算します。
$P_B=\sqrt{ 3 } V_BI_n=\sqrt{ 3 } ×33×I_n=10000$
$I_n=\displaystyle \frac{ 10000 }{ \sqrt{ 3 } ×33}=175$[A]
三相短絡電流 IS を計算します。
$I_S=I_n×\displaystyle \frac{ 100 }{ \%X }=175×\displaystyle \frac{ 100 }{ 40}=438$[A]
答え (5)
2002年(平成14年)問12
容量 50[KV・A]、一次側及び二次側の定格電圧がそれぞれ 3.64[kV]及び 200[V]、短絡インピーダンス(百分率インピーダンス降下) 5[%]の単相変圧器3台を、図のように一次側Y、二次側△に結線している。この変圧器群の一次側に 6.3[KV]の三相交流電源を接続して、二次側に接続された 120[kW]の平衡した三相抵抗負荷に電力を供給しているとき、次の(a)及び(b)に答えよ。
ただし、変圧器の損失は無視するものとする。
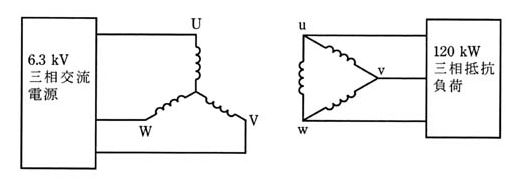
(a) この単相変圧器の一次側巻線に流れている電流[A]の値として、最も近いのは次のうちどれか。
(1) 6.3 (2) 11 (3) 19 (4) 33 (5) 200
(b) 負荷が接続されている端子で三相短絡が発生したとき、短絡点に流れる短絡電流[KA]の値として、最も近いのは次のうちどれか。
(1) 2.9 (2) 5.0 (3) 7.1 (4) 8.7 (5) 15
2002年(平成14年)問12 過去問解説
(a) 一次側の線間電圧を V1 とすると、
$V_1=\sqrt{ 3 } ×3.64≒6.3$[kV]
一次側巻線に流れている電流を I1 とすると
$P=\sqrt{ 3 }V_1I_1$
$120=\sqrt{ 3 }×6.3×I_1$
$I_1≒11$[A]
答え (2)
(b) 短絡点の線間電圧を基準電圧 VB とします。
$V_B=200$ [V]
基準容量 PB を設定します。
$P_B=3×50$[KV・A]
基準容量 PB と基準電圧 VB から、定格電流 In を計算します。
$P_B=\sqrt{ 3 } V_BI_n=\sqrt{ 3 } V_{2n}I_n$
$I_n=\displaystyle \frac{3×50×10^3 }{ \sqrt{ 3 } ×200}$
三相短絡電流 IS を計算します。
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }$
$I_S=\displaystyle \frac{3×50×10^3 }{ \sqrt{ 3 } ×200}×\displaystyle \frac{ 100 }{ 5 }=8700$
答え (4)
2003年(平成15年)問10
線間電圧 V[V]の三相3線式送電線で、負荷端から電源側をみた百分率インピーダンスを %Z とするとき、負荷端での三相短絡電流[A]を表す式として、正しいのは次のうちどれか。
ただし、基準容量は Pn[V・A]とする。
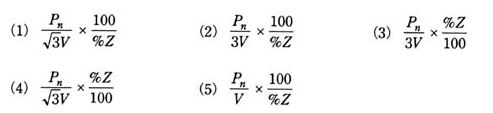
2003年(平成15年)問10 過去問解説
負荷端を基準電圧 VB=V とすると、定格電流 In は、
$I_n=\displaystyle \frac{ P_B }{ \sqrt{ 3 } V}$
三相短絡電流 IS は、
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }$
$I_S=\displaystyle \frac{ P_n }{ \sqrt{ 3 } V}×\displaystyle \frac{ 100 }{ \%Z }$
答え (1)
2004年(平成16年)問16
図のように、定格電圧 66[kV]の電源から三相変圧器を介して二次側に遮断器が接続された系統がある。この三相変圧器は定格容量 10[MV・A]、変圧比 66/6.6[kV]、百分率インピーダンスが自己容量基準で 7.5[%]である。変圧器一次側から電源側をみた百分率インピーダンス基準容量 100[MV・A]で 5[%]とするとき、次の(a)及び(b)に答えよ。

(a) 基準容量を 10[MV・A]として、変圧器二次側から電源側をみた百分率インピーダンス[%]の値として正しいのは次のうちどれか。
(1) 2.5 (2) 5.0 (3) 7.0 (4) 8.0 (5) 12.5
(b) 図のA点で三相短絡事故が発生したとき、事故電流を遮断できる遮断器の定格遮断電流[kA]の最小値として、正しいは次のうちどれか。ただし、変圧器二次側からA点までのインピーダンスは無視するものとする。
(1) 8 (2) 12.5 (3) 16 (4) 20 (5) 25
2004年(平成16年)問16 過去問解説
(a) 変圧器一次側からみた百分率インピーダンスを基準容量 10MV・Aに変換したときの百分率インピーダンスを %Z’ とすると、
$\%Z’=5×\displaystyle \frac{ 10 }{ 100}=0.5$[%]
変圧器二次側から電源側をみた百分率インピーダンス( %Z )は、
$\%Z =0.5+7.5 =8.0$[%]
答え (4)
(b) 基準容量 PB と基準電圧 VB から、定格電流 In は
$P_B=\sqrt{ 3 } V_BI_n=\sqrt{ 3 } V_{2n}I_n$
$I_n=\displaystyle \frac{ 10×10^6 }{ \sqrt{ 3 } ×6600}=875$[A]
三相短絡電流 IS は、
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }$
$I_S=875×\displaystyle \frac{ 100 }{ 8 }=10900$[A]
点Aで三相短絡事故が発生したとき、事故電流を遮断できる遮断器の定格遮断電流 I は、三相短絡電流 IS の直近上位の値となります。
答え (2)
2006年(平成18年)問17
図のような系統において、昇圧用変圧器の容量は 30[MV・A]、変圧比は 11[kV]/33[kV]、百分率インピーダンスは自己容量基準で 7.8[%]、計器用変流器(CT)の変流比は 400[A]/5[A]である。系統の点Fにおいて、三相短絡事故が発生し、1800[A]の短絡電流が流れたとき、次の(a)及び(b)に答えよ。
ただし、CTの磁気飽和は考慮しないものとする。
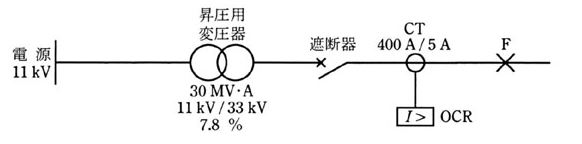
(a) 系統の基準容量を 10[MV・A]としたとき、事故点Fから電源側をみた百分率インピーダンス[%]の値として、最も近いのは次のうちどれか。
(1) 5.6 (2) 9.7 (3) 12.3 (4) 29.2 (5) 37.0
(b) 過電流継電器(OCR)を 0.09[s]で動作させるには、OCRの電流タップ値を何アンペアの位置に整定すればよいか。正しい値を次のうちから選べ。
ただし、OCRのタイムレバー位置は 3 に整定されており、タイムレバー位置 10 における限時特性は図示のとおりである。
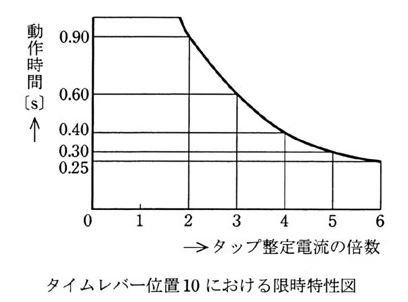
(1) 3.0[A] (2) 3.5[A] (3) 4.0[A] (4) 4.5[A] (5) 5.0[A]
2006年(平成18年)問17 過去問解説
(a) 基準容量を PB=30 [MV・A]と基準電圧 VB=33[kV]とし、定格電流 In を計算します。
$P_B=\sqrt{ 3 } V_BI_n$
$I_n=\displaystyle \frac{ 30×10^6 }{ \sqrt{ 3 } ×33×10^3}=525$[A]
三相短絡電流 IS とすると、
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }$
$1800=525×\displaystyle \frac{ 100 }{ \%Z }$
$\%Z=29.2$[%]
この %Z は、基準容量 30MV・A のときの値であるから、10MV・A に換算すると、
$\%Z’=29.2×\displaystyle \frac{ 10 }{ 30 }=9.73$[%]
答え (2)
(b) 短絡電流は IS=1800[A]、CTの変流比は 400/5[A]であるから、CTの二次側の電流 I2[A]は、
$I_2=1800×\displaystyle \frac{ 5 }{ 400 }=22.5$[A]
タイムレバー位置 3 で、OCRを 0.09[s]で動作させるためには、
$0.09×\displaystyle \frac{ 10 }{ 3 }=0.3$[s]
図より動作時間 0.3[s]のときのタップ整定電流の倍数は 5 であるから、電流タップ値[A]は、
$\displaystyle \frac{ 22.5 }{5 }=4.5$[A]
答え (4)
2007年(平成19年)問12
図のような三相3線式配電系統がある。配電用変電所の変圧器容量は 10000[kV・A]、変圧比は 66[kV]/6.6[kV]、百分率リアクタンスは自己容量基準で 7.5[%]であり、配電用変電所より上位系統側の百分率インピーダンスは基準容量 10000[kVA]で 0.5[%]とする。配電系統の末端L点には負荷(抵抗負荷とする)が接続されており、配電用変電所の引出口F点からL点までの百分率インピーダンスは基準容量 10000[kVA]で 10[%]とする。F点において三相完全短絡事故が発生したとき、F点における短絡電流[kA]の値として、最も近いのは次のうちどれか。
ただし、百分率インピーダンスは抵抗分を無視するものとする。
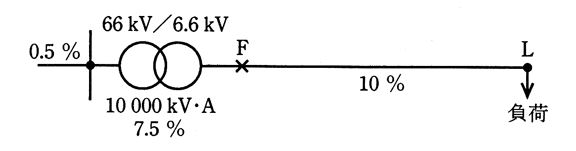
(1) 4.9 (2) 8.7 (3) 10.9 (4) 11.7 (5) 12.5
2007年(平成19年)問12 過去問解説
短絡事故があった点Fからみた、上位系統の百分率インピーダンスは、
$\%Z=0.5+7.5=8.0$[%]
基準電圧 VB=6.6[kV]とし、定格電流 In を計算します。
$P_B=\sqrt{ 3 } V_BI_n$
$I_n=\displaystyle \frac{ 10000×10^3 }{ \sqrt{ 3 } ×6.6×10^3}=875$[A]
三相短絡電流 IS は、
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }$
$I_S=875×\displaystyle \frac{ 100 }{ 8 }=10900$[A]
答え (3)
2008年(平成20年)問8
一次電圧 66[kV]、二次電圧 6.6[kV]、容量 80[MV・A]の三相変圧器がある。一次側に換算した誘導性リアクタンスの値が 4.5[Ω]のとき、百分率リアクタンスの値[%]として、最も近いのは次のうちどれか。
(1) 2.8 (2) 4.8 (3) 8.3 (4) 14.3 (5) 24.8
2008年(平成20年)問8 過去問解説
一次電圧を V1n 、容量を P、一次側に換算した誘導性リアクタンスリアクタンスを X1 とすると、百分率リアクタンスの値 %X[%]は、
$\begin{eqnarray}\%X &=& \displaystyle \frac{ PX_1 }{V_{1n}^2}×100 \\&=& \displaystyle \frac{ 80×10^6×4.5 }{(66×10^3)^2}×100≒8.3[%]\end{eqnarray}$
答え (3)
2009年(平成21年)問16
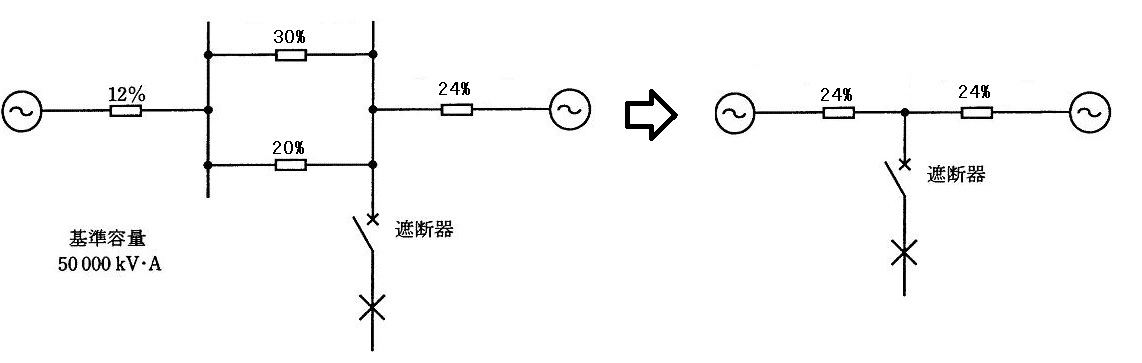
図のような交流三相3線式の系統がある。各系統の基準容量と基準容量をベースにした百分率インピーダンスが図に示された値であるとき、次の(a)及び(b)に答えよ。
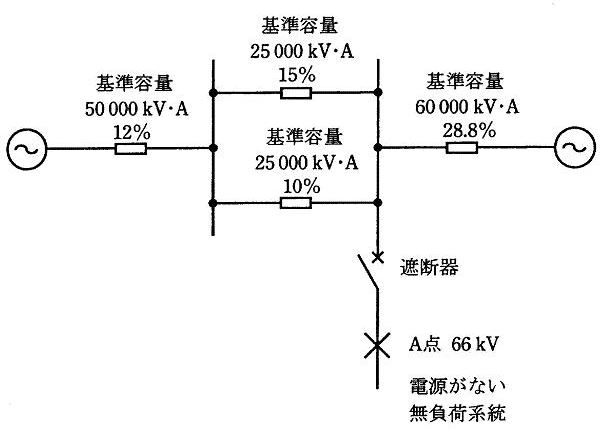
(a) 系統全体の基準容量を 50000[kV・A]に統一した場合、遮断器の設置場所からみた合成百分率インピーダンス[%]の値として、正しいのは次のうちどれか。
(1) 4.8 (2) 12 (3) 22 (4) 30 (5) 48
(b) 遮断機の投入後、A点で三相短絡事故が発生した。三相短絡電流[A]の値として、最も近いのは次のうちどれか。
ただし、線間電圧は 66[kV]とし、遮断器からA点までのインピーダンスは無視するものとする。
(1) 842 (2) 911 (3) 1458 (4) 2104 (5) 3645
2009年(平成21年)問16 過去問解説
(a) 基準容量を 50000[kV・A]に統一した場合の各負荷の百分率インピーダンス[%]は
25000[kV・A]、15[%]は
$15×\displaystyle \frac{ 50000 }{ 25000 }=30$[%]
25000[kV・A]、10[%]は
$10×\displaystyle \frac{ 50000 }{ 25000 }=20$[%]
60000[kV・A]、28.8[%]は
$28.8×\displaystyle \frac{ 50000 }{ 60000 }=24$[%]
遮断器より左側の合成百分率インピーダンス Z1 は[%]は
$Z_1=12+\displaystyle \frac{ 30×20 }{ 30+20}=24$[%]
合成百分率インピーダンス %Z は[%]は
$\%Z=\displaystyle \frac{ 24×24 }{ 24+24}=12$[%]
答え (2)
(b) 三相短絡電流 IS は、
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }$
$I_S=\displaystyle \frac{ 50000×10^3 }{ \sqrt{ 3 } ×66×10^3}×\displaystyle \frac{ 100 }{ 12}=3645$[A]
答え (5)
2011年(平成23年)問16
変電所に設置された一次電圧 66[kV]、二次電圧 22[kV]、容量 50[MV・A]の三相変圧器に、22[kV]の無負荷の線路が接続されている。その線路が、変電所から負荷側 500[m]の地点で三相短絡を生じた。
三相変圧器の結線は、一次側と二次側がY-Y結線となっている。
ただし、一次側からみた変圧器の1相当たりの抵抗は 0.018[Ω]、リアクタンスは 8.73[Ω]、故障が発生した線路の1線当たりのインピーダンスは(0.20+j0.48)[Ω/km]とし、変圧器の一次電圧側の線路インピーダンス及びその他の値は無視するものとする。次の(a)及び(b)の問に答えよ。
(a) 短絡電流[kA]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.83 (2) 1.30 (3) 1.42 (4) 4.00 (5) 10.5
(b) 短絡前に、22[kV]に保たれていた三相変圧器の母線の線間電圧は、三相短絡故障したとき、何[kV]に低下するか。電圧[kV]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 2.72 (2) 4.71 (3) 10.1 (4) 14.2 (5) 17.3
2011年(平成23年)問16 過去問解説
(a) 問題文を図に示します。
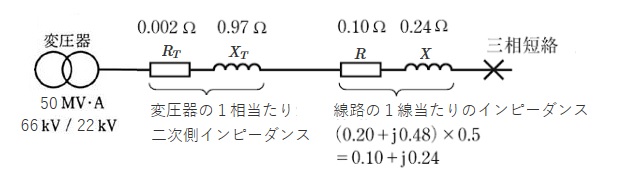
1相当たりの変圧器1次側の容量と2次側の容量はY-Y結線ですので、等しくなります。1次側の電流,電圧を I1,V1、2次側の電流,電圧を I_2,V2 とすると、
$P=I_1×\displaystyle \frac{ V_1 }{\sqrt{ 3 } }=I_2×\displaystyle \frac{ V_2 }{\sqrt{ 3 } }$
1次側からみた1相当たりの抵抗を R1[Ω]、2次側に換算した1相当たりの抵抗を RT[Ω]とすると、
$I_1=\displaystyle \frac{ V_1 }{\sqrt{ 3 }R_1 }$
$I_2=\displaystyle \frac{ V_2 }{\sqrt{ 3 }R_T }$
$P=I_1×\displaystyle \frac{ V_1 }{\sqrt{ 3 } }=I_2×\displaystyle \frac{ V_2 }{\sqrt{ 3 } }$より
$\displaystyle \frac{ V_1 }{\sqrt{ 3 }R_1 }×\displaystyle \frac{ V_1 }{\sqrt{ 3 } }=\displaystyle \frac{ V_2 }{\sqrt{ 3 }R_T }×\displaystyle \frac{ V_2 }{\sqrt{ 3 } }$
$\displaystyle \frac{ V_1^2 }{R_1 }=\displaystyle \frac{ V_2^2 }{R_T }$
$R_T=R_1×\displaystyle \frac{V_2^2 }{V_1^2 }=0.018×\displaystyle \frac{ 22×10^3 }{ 66×10^3 }=0.002$[Ω]
1次側からみた1相当たりのリアクタンスを X1[Ω]、2次側に換算した1相当たりのリアクタンスを XT[Ω]とすると、抵抗の場合と同じように考えれますので、
$X_T=X_1×\displaystyle \frac{V_2^2 }{V_1^2 }=8.73×\displaystyle \frac{ 22×10^3 }{ 66×10^3 }=0.97$[Ω]
2次側の合成インピーダンスを Z[Ω]とすると、
$\begin{eqnarray}Z&=&\sqrt{(R+R_T)^2+(X+X_T)^2}\\\\&=&\sqrt{(0.1+0.002)^2+(0.24+0.97)^2}\\\\&=&1.214[Ω]\end{eqnarray}$
三相短絡電流 IS[A]は、
$I_S=\displaystyle \frac{ V_2 }{\sqrt{ 3 }×Z }=\displaystyle \frac{ 22000 }{\sqrt{ 3 }×1.214 }=10461$ [A]
答え (5)
(b) 線路の合成インピーダンスを Z2[Ω]とすると、
$Z_2=\sqrt{R^2+X^2}=\sqrt{0.1^2+0.24^2}=0.26$[Ω]
相電圧を E2[V]とすると、線路の合成インピーダンス Z2[Ω]に短絡電流 IS[A]が流れたときの、相電圧 E2 が電圧降下になります。
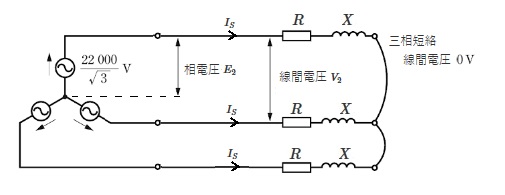
$E_2=Z_2I_S=2720×10461=2720$[V]
よって、線間電圧 V2[V]は、
$V_2=\sqrt{3}E_2=4710$[V]
答え (2)
2013年(平成25年)問17
図に示すように、定格電圧 66[kV] の電源から送電線と三相変圧器を介して、二次側に遮断機が接続された系統を考える。三相変圧器の電気的特性は、定格容量 20[MV・A]、一次側線間電圧 66[kV]、二次側線間電圧 6.6[kV]、自己容量基準での百分率リアクタンス 15.0[%]である。一方、送電線から電源側をみた電気的特性は、基準容量 100[MV・A] の百分率インピーダンスが 5.0[%] である。このとき、次の(a)及び(b)の問に答えよ。
ただし、百分率インピーダンスの抵抗分は無視するものとする。
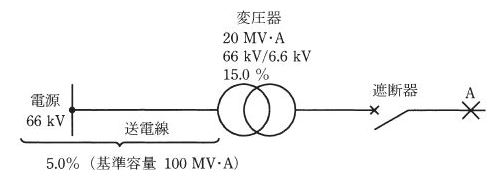
(a) 基準容量を 10[MV・A] としたとき、変圧器の二次側から電源側をみた百分率リアクタンス[%]の値として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1) 2.0 (2) 8.0 (3) 12.5 (4) 15.5 (5) 20.0
(b) 図のAで三相短絡事故が発生したとき、事故電流[kA]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、変圧器の二次側からAまでのインピーダンス及び負荷は、無視するものとする。
(1) 4.4 (2) 6.0 (3) 7.0 (4) 11 (5) 44
2013年(平成25年)問17 過去問解説
(a) 変圧器の百分率リアクタンス[%]は
$15×\displaystyle \frac{ 10 }{ 20 }=7.5$[%]
送電線の百分率リアクタンス[%]は
$5.0×\displaystyle \frac{ 10 }{ 100 }=0.5$[%]
合成百分率リアクタンス %Z[%]は
$\%Z=7.5+0.5=8.0$[%]
答え (2)
(b) 基準容量が 10MV・A のとき、定格電流 In は、
$P_B=\sqrt{ 3 } V_BI_n=\sqrt{ 3 } V_{2n}I_n$
$I_n=\displaystyle \frac{ 10×10^6 }{ \sqrt{ 3 } ×6600}=875$[A]
三相短絡電流 IS は、
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }$
$I_S=875×\displaystyle \frac{ 100 }{ 8 }=10900$[A]
答え (4)
2016年(平成28年)問16
図に示すように、発電機、変圧器と公称電圧66kVで運転される送電線からなる系統があるとき、次の(a)及び(b)の問に答えよ。
ただし、中性点接地抵抗は図の変圧器のみに設置され、その値は 300Ω とする。
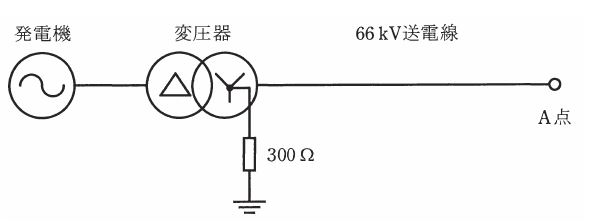
(a) A点で100Ωの抵抗を介して一線地絡事故が発生した。このときの地絡電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、発電機、発電機と変圧器間、変圧器及び送電線のインピーダンスは無視するものとする。
(1) 95 (2) 127 (3) 165 (4) 381 (5) 508
(b) A点で三相短絡事故が発生した。このときの三相短絡電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、発電機の容量は 10000kV・A、出力電圧 6.6kV、三相短絡時のリアクタンスは自己容量ベースで 25%、変圧器容量は 10000kV・A、変圧比は 6.6kV/66kV、リアクタンスは自己容量ベースで 10%、66kV送電線のリアクタンスは、10000kV・Aベースで5%とする。
なお、発電機と変圧器間のインピーダンスは無視する。また、発電機、変圧器及び送電線の抵抗は無視するものとする。
(1) 33 (2) 219 (3) 379 (4) 656 (5) 3019
2016年(平成28年)問16 過去問解説
(a) 問題文を図に示します。
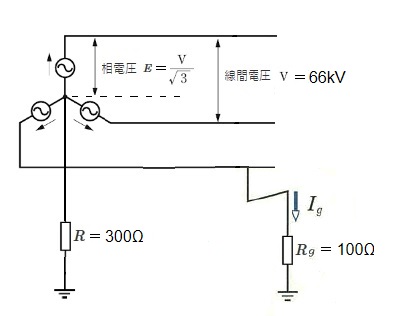
$I_g=\displaystyle \frac{ E }{ R+R_g}=\displaystyle \frac{ \displaystyle \frac{ 66000 }{ \sqrt{3}} }{ 300+100}=95$[A]
答え (1)
(b) 問題文を図に示します。
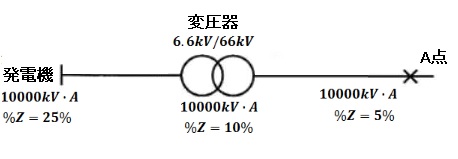
容量はすべて 10000kV・Aなので、短絡点から電源側の合成%インピーダンス( %Z )は、
$\%Z=5+10+25=40$[%]
基準容量 PB=10000[kV・A]と基準電圧 VB=66[kV]から、定格電流 In[A]は、
$P_B=\sqrt{ 3 } V_BI_n$
$I_n=\displaystyle \frac{ 10000×10^3 }{ \sqrt{ 3 } ×66×10^3 }=87.48$[A]
三相短絡電流 IS[A]は、
$I_S=I_n×\displaystyle \frac{ 100 }{ \%Z }=87.48×\displaystyle \frac{ 100 }{ 40 }=219$[A]
答え (2)





