第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「相互インダクタンス」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「相互インダクタンス」の過去問題も解説しています。
相互誘導と相互インダクタンス
相互誘導作用
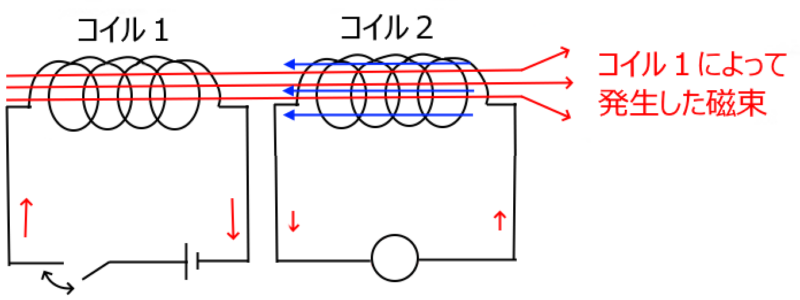
図のような、コイルを含む回路が2つあります。左の回路には電源が付いてますが、右の回路には電源がありません。
左の回路(1次コイル)のスイッチを入れれば、コイル内部に磁界が発生します。右の回路(2次コイル)があまり離れてなければ、1次コイルの磁界が2次コイルに影響を与えます。
1次コイルの電流が一定なら何も起こりませんが、スイッチの開閉によって電流が変化すると、1次コイルの磁界が変化し、2次コイルは電磁誘導が起こります。そして、電源の無いはずの右の回路に電流が流れます。この現象を「相互誘導」といいます。
相互インダクタンス
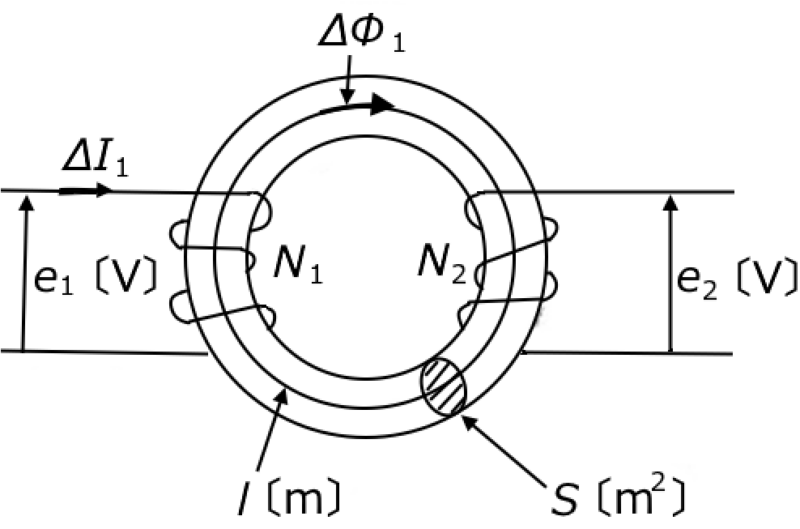
図にように環状鉄心に巻かれた1次コイルと2次コイルの巻数を $N_1$ 、$N_2$ とし、コイルの断面積を $S$[m2]、コイルの長さ $l$[m]、1次コイル $L_1$ に流れる電流を $ΔI_1$[A]とします。
ファラデーの電磁誘導の法則より、時間 $Δt $[s]の間にコイルを貫く磁束が $Δ ϕ _1$[Wb]だけ変化するとき、2次コイルに発生する誘導起電力 $e_2$[V]は、次のように表されます。
$e_2=-N_2\displaystyle\frac{Δ ϕ _1}{Δt}$[V]
磁気回路のオームの法則は次のように表されます。
$R_{ m }=\displaystyle \frac{ N_1ΔI}{ Δ ϕ _1}=\displaystyle \frac{ l}{ μS}$
$Δ ϕ _1=\displaystyle\frac{μSN_1ΔI}{l }$[Wb]
この式を$e_2=-N_2\displaystyle\frac{Δ ϕ _1}{Δt}$に代入すると、
$e_2=-N_2\displaystyle\frac{1}{Δt}×\displaystyle\frac{μSN_1ΔI}{l }=-\displaystyle\frac{μSN_1N_2}{l}\frac{ΔI}{Δt}$[V]
この $\displaystyle\frac{μSN_1N_2}{l}$ を「相互インダクタンス」といい、記号 $M$(単位 ヘンリー[H])で表します。
$M=\displaystyle\frac{μSN_1N_2}{l}$[H]
コイルに発生する誘導起電力を求める公式
2次コイルに発生する起電力 $e_2$ は、1次コイルに流れる電流の変化に影響し、$Δt$ 秒間に $ΔI_1$ だけ変化した場合、次のように表されます。
$e_2=-M\displaystyle\frac{ΔI_1}{Δt}$[V]
$e_2$[V]:コイル $N_2$ に発生する誘導起電力
$M$[H]:相互インダクタンス
$ΔI_1$[A]:変化した電流の量
$Δt$[s]:電流が変化するのに要した時間
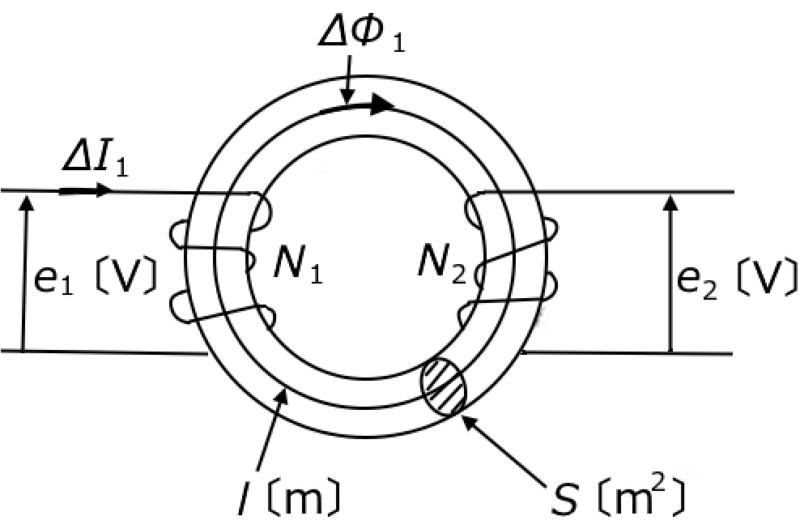
ファラデーの法則より
$e_2=-N_2\displaystyle\frac{Δ ϕ _1}{Δt}=-M\frac{ΔI_1}{Δt}$[V]$M=N_2\displaystyle\frac{Δ ϕ _1}{ΔI_1}$[H]
と表わすこともできます。
インダクタンスの結合係数
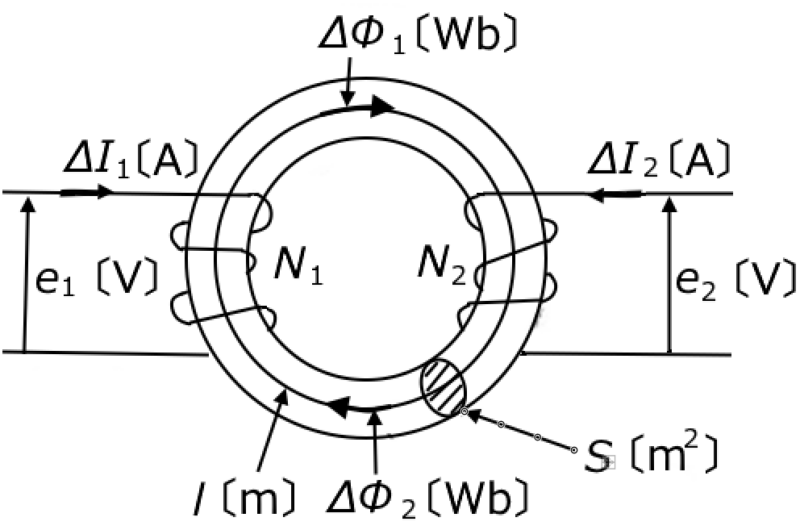
1次コイルに$ΔI_1$[A]の電流を流したとき、$Δ ϕ _1$[Wb]の磁束が発生するとします。この磁束がすべて2次コイルと鎖交するとすれば、
$L_1=N_1\displaystyle\frac{Δ ϕ _1}{ΔI_1}$[H]
$M=N_2\displaystyle\frac{Δ ϕ _1}{ΔI_1}$[H]
となります。
2次コイルに$ΔI_2$[A]の電流を流したとき、$Δ ϕ _2$[Wb]の磁束が発生するとします。この磁束がすべて1次コイルと鎖交するとすれば、
$L_2=N_2\displaystyle\frac{Δ ϕ _2}{ΔI_2}$[H]
$M=N_1\displaystyle\frac{Δ ϕ _2}{ΔI_2}$[H]
となります。
これらの式より
$\begin{eqnarray}L_1×L_2&=&\left(N_1\displaystyle\frac{Δ ϕ _1}{ΔI_1}\right)×\left(N_2\displaystyle\frac{Δ ϕ _2}{ΔI_2}\right)\\\\&=&\left(N_2\displaystyle\frac{Δ ϕ _1}{ΔI_1}\right)×\left(N_1\displaystyle\frac{Δ ϕ _2}{ΔI_2}\right)\\\\&=&M^2\end{eqnarray} $
$M=\displaystyle\sqrt{L_1L_2}$
しかし、普通はいくらかの漏れ磁束が発生します。二つの磁束の結びつきを示すのに、「結合係数」(記号 $k$ )を使って表します。
$M=k\displaystyle\sqrt{L_1L_2}$
結合係数 $ k $ は $0<k≦1$ の範囲になります。
相互インダクタンス、自己インダクタンス、結合係数 の関係を表す公式
$M=k\displaystyle\sqrt{L_1L_2}$
$M$[H]:相互インダクタンス
$L_1$[H]:コイル1の自己インダクタンス
$L_2$[H]:コイル2の自己インダクタンス
$k$:結合係数
結合係数 $k$ は2つのコイル間の漏れ磁束の割合をあらわしたもので、一方のコイルに発生した磁束の全て(100%) が、もう一方のコイルを貫く状態のことを「漏れ磁束無し」といい、漏れ磁束無しのときの結合係数は $k=1$ になります。
インダクタンスの和動接続と差動接続
1次コイルと2次コイルがつくる磁界が同じ向きになる接続方法を「和動接続」といい、磁界の向きが逆になるような接続方法を「差動接続」といいます。
和動接続
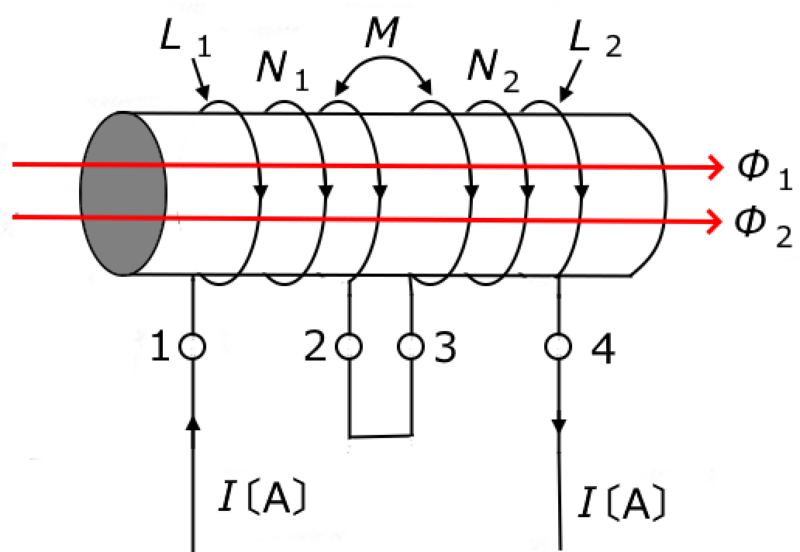
端子1-4から見た全体の合成インダクタンスは次のようになります。
$\begin{eqnarray}L&=&N_1\displaystyle\frac{ ϕ _1+ ϕ _2}{I}+N_2\displaystyle\frac{ ϕ _1+ ϕ _2}{I}\\\\&=&N_1\displaystyle\frac{ ϕ _1}{I}+N_1\displaystyle\frac{ ϕ _2}{I}+N_2\displaystyle\frac{ ϕ _1}{I}+N_2\displaystyle\frac{ ϕ _2}{I}\\\\&=&L_1+M+M+L_2\\\\&=&L_1+L_2+2M\end{eqnarray} $
差動接続
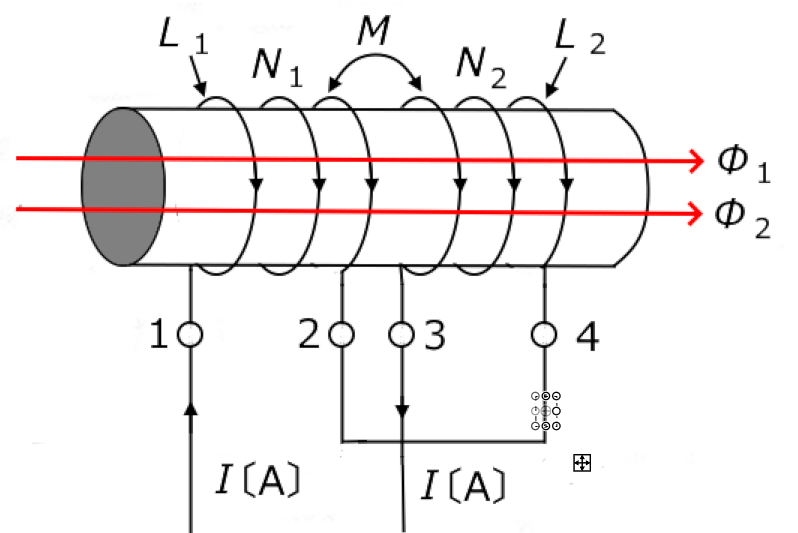
端子1-3間の全体の合成インダクタンスは次のようになります。
$\begin{eqnarray}L&=&N_1\displaystyle\frac{ ϕ _1- ϕ _2}{I}+N_2\displaystyle\frac{ ϕ _2- ϕ _1}{I}\\\\&=&N_1\displaystyle\frac{ ϕ _1}{I}-N_1\displaystyle\frac{ ϕ _2}{I}+N_2\displaystyle\frac{ ϕ _2}{I}-N_2\displaystyle\frac{ ϕ _1}{I}\\\\&=&L_1-M+L_2-M\\\\&=&L_1+L_2-2M\end{eqnarray} $
電験三種-理論の過去問解説:相互インダクタンス
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1999年(平成11年)問2【電験理論の過去問題】
A、B二つのコイルがあり、Aコイルに流れる電流 i[A]を 1/1000 秒間に 40[mA]変化させている間、Bコイルに 0.3[V]の起電力を発生する。この両コイル間の相互インダクタンス M[mH]の値として、正しいのは次のうちどれか。
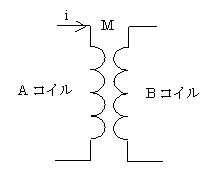
(1) 0.65 (2) 0.75 (3) 5.5 (4) 6.5 (5) 7.5
2次コイルに発生する起電力 $e_2$は、1次コイルに流れる電流の変化に影響し、$Δt$秒間に $ΔI_1$だけ変化した場合、次のように表されます。
$|e_2|=M\displaystyle\frac{ΔI_1}{Δt}$
$M=e_2\displaystyle\frac{Δt}{ΔI_1}=0.3×\displaystyle\frac{1×10^{-3}}{0.04}=7.5×10^{-3}=7.5$[mH]
答え (5)
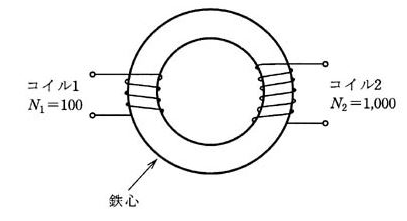
2003年(平成15年)問4【電験理論の過去問題】
図のように、環状鉄心にコイル1及びコイル2が巻かれている。コイル1、コイル2の自己インダクタンスをそれぞれ $L_1$、$L_2$とし、その巻数をそれぞれ $N_1=100$、$N_2=1000$としたとき、$L_1=1×10^{-3}$[H]であった。このとき、自己インダクタンス $L_2$[H]の値と、コイル1とコイル2の相互インダクタンス $M$[H]の値として、正しいものを組み合わせたのは次のうちどれか。
ただし、鉄心は等断面、等質であり、コイル及び鉄心の漏れ磁束はないものとする。

自己インダクタンス $L$ は、
$L=\displaystyle\frac{μSN^2}{l}=\displaystyle\frac{N^2}{R_{ m }}$
ですので、$L_1$ と $L_2$ は
$L_1=\displaystyle\frac{N_1^2}{R_{ m }}$
$L_2=\displaystyle\frac{N_2^2}{R_{ m }}$
となります。2式より、
$\displaystyle\frac{N_1^2}{L_1}=\displaystyle\frac{N_2^2}{L_2}$
${L_2}=\displaystyle\frac{N_2^2}{N_1^2}×{L_1}=\displaystyle\frac{1000^2}{100^2}×1×10^{-3}=1×10^{-1}$
磁束の漏れがないときの、自己インダクタンス$L_1$ 、 $L_2$ と相互インダクタンス $M$ の関係は、
$M=\displaystyle\sqrt{L_1L_2}=\displaystyle\sqrt{1×10^{-3}×1×10^{-1}}=1×10^{-2}$
答え (1)
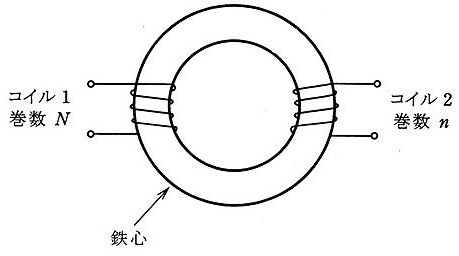
2008年(平成20年)問4【電験理論の過去問題】
図のように、環状鉄心に二つのコイルが巻かれている。コイル1の巻数は $N$ であり、その自己インダクタンスは $L$[H]である。コイル2の巻数は $n$であり、その自己インダクタンスは $4L$[H]である。巻数 $n$ の値を表す式として、正しいのは次のうちどれか。
ただし、鉄心は等断面、等質であり、コイル及び鉄心の漏れ磁束はなく、また鉄心の磁気飽和もないものとする。
(1) $\displaystyle\frac{N}{4}$ (2) $\displaystyle\frac{N}{2}$ (3) 2N (4) 4N (5) 16N
自己インダクタンス $L$ は、
$L=\displaystyle\frac{μSN^2}{l}=\displaystyle\frac{N^2}{R_{ m }}$
ですので、$L_1$ と $L_2$ は
$L_1=\displaystyle\frac{N^2}{R_{ m }}=L$
$L_2=\displaystyle\frac{n^2}{R_{ m }}=4L$
となります。2式より、
$\displaystyle4\frac{N^2}{R_{ m }}=\displaystyle\frac{n^2}{R_{ m }}$
$n^2=2N$
答え (3)
2012年(平成24年)問3【電験理論の過去問題】
次の文章は、コイルのインダクタンスに関する記述である。ここで、鉄心の磁気飽和は、無視するものとする。
均質で等断面の環状鉄心に被覆電線を巻いてコイルを作製した。このコイルの自己インダクタンスは、巻数の( ア )に比例し、磁路の( イ )に反比例する。
同じ鉄心にさらに被覆電線を巻いて別のコイルを作ると、これら二つのコイル間には相互インダクタンスが生じる。相互インダクタンスの大きさは、漏れ磁束が( ウ )なるほど小さくなる。それぞれのコイルの自己インダクタンスを $L_1 $[H]、$L_2$ [H]とすると、相互インダクタンスの最大値は( エ )[H]である。
これら二つのコイルを( オ )とすると、合成インダクタンスの値は、それぞれの自己インダクタンスの合計値よりも大きくなる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
| (1) | 1乗 | 断面積 | 少なく | $L1+L2$ | 差動接続 |
| (2) | 2乗 | 長さ | 多く | $L1+L2$ | 和動接続 |
| (3) | 1乗 | 断面積 | 少なく | $\sqrt{L_1L_2}$ | 和動接続 |
| (4) | 2乗 | 長さ | 多く | $L1+L2$ | 差動接続 |
| (5) | 2乗 | 長さ | 多く | $\sqrt{L_1L_2}$ | 和動接続 |
自己インダクタンス $L$ は、
$L=\displaystyle\frac{μSN^2}{l}$
ですので、巻数の( 2乗 )に比例し、磁路の( 長さ )に反比例します。
漏れ磁束の大小は、二つの磁束の結びつきを示す、結合係数 $k$ を使って表します。
$M=k\displaystyle\sqrt{L_1L_2}$
結合係数 $ k $ は $0<k≦1$ の範囲です。相互インダクタンスの大きさは、漏れ磁束が( 多く )なるほど小さくなる。相互インダクタンスの最大値はk=1のときで、( $\sqrt{L_1L_2}$ )[H]です。
インダクタンスの直列接続には和動接続と差動接続があります。
和動接続は、$L_1+L_2+2M$
差動接続は、$L_1+L_2-2M$
です。それぞれの自己インダクタンスの合計値よりも大きくなるのは、( 和動接続 )です。
答え (5)
2017年(平成29年)問3【電験理論の過去問題】
環状鉄心に、コイル1及びコイル2が巻かれている。二つのコイルを図1のように接続したとき、端子A-B間の合成インダクタンスの値は $1.2H$ であった。次に、図2のように接続したとき、端子C-D間の合成インダクタンスの値は $2.0H$ であった。このことから、コイル1の自己インダクタンス $L$ の値[H]、コイル1及びコイル2の相互インダクタンス $M$ の値[H]の組合せとして、正しいものを次の( 1 )~( 5 )のうちから一つ選べ。
ただし、コイル1及びコイル2の自己インダクタンスはともにL[H]、その巻数をNとし、また、鉄心は等断面、等質であるとする。
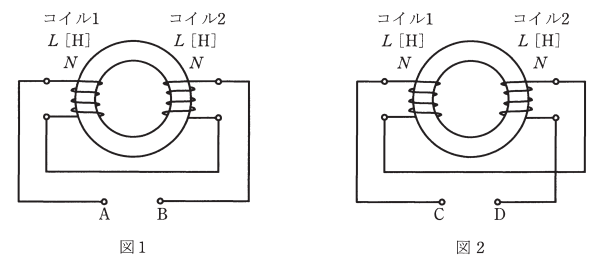

端子A-B間の合成インダクタンスを $L_{AB}$[H],端子C-D間の合成インダクタンスを $L_{CD}$[H]とすると、図1は差動接続、図2は和動接続ですので、
$L_{AB}=L+L-2M=2L-2M=1.2$[H]
$L_{CD}=L+L+2M=2L+2M=2.0$[H]
この連立方程式を解くと、$L=0.8$[H],$M=0.2$[H]
答え(2)
電験三種の理論科目に出題される「電磁気分野」のページ
1.磁力線と磁束
2.アンペールの法則
3.フレミングの左手の法則
4.電流が磁界から受ける力
5.ヒステリシス曲線と損失
6.電磁誘導(レンツの法則とファラデーの法則)
7.自己インダクタンス
8.相互インダクタンス
9.磁気エネルギー






