第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「ヒステリシス曲線と損失」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「ヒステリシス曲線と損失」の過去問題も解説しています。
磁性体と非磁性体
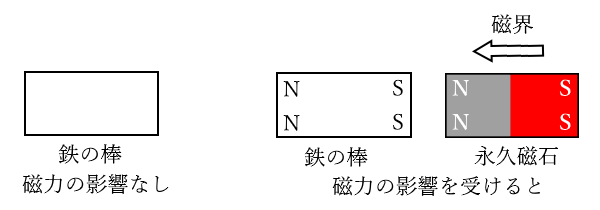
磁力を持たない鉄の棒に永久磁石を近づけると、鉄の棒に永久磁石のN極に近い側にS極が現れ、反対側にN極が現れます。このような現象を「磁気誘導」といいます。
はじめは磁力を持っていなかった鉄の棒が、外部の磁力の影響を受けて磁石のように変化することを「磁化」といいます。
磁化のされやすさは物質によって異なります。永久磁石を近づけると、磁化されやすい性質を持っている物質を「磁性体」といい、磁化されない物質を「非磁性体」といいます。
強磁性体
鉄やニッケル、コバルトなどは外部磁気の影響を強く受けて磁化されます。このような物質を「強磁性体」といいます。強磁性体の透磁率は真空の透磁率の数百倍以上です。
強磁性体は、外部磁気を取り除いても磁化の影響が残り永久磁石に変化するものと、磁化の影響が少ししか残らないものがあります。
比透磁率 $μ_S>>0$
常磁性体
アルミニウムやすず、白金などは強磁性体ほど強くは磁化されない物質です。強力な磁場をかけないと磁化されているのかどうかが分からないほどです。このような物質を「常磁性体」といい、外部磁気を取り除くと、磁化の影響は残りません。
比透磁率 $μ_S>0$
反磁性体
銀、銅、鉛 などの物質は磁化される方向が磁場の向きと、わずかに逆になります。このような物質を「反磁性体」といいます。反磁性体に磁石を近づけると反発しますが、強力な磁場をかけないと磁化されているかどうか分からないほどです。常磁性体と同様に外部磁気を取り除くと、磁化の影響は残りません。
比透磁率 $μ_S<0$
強磁性体の磁化
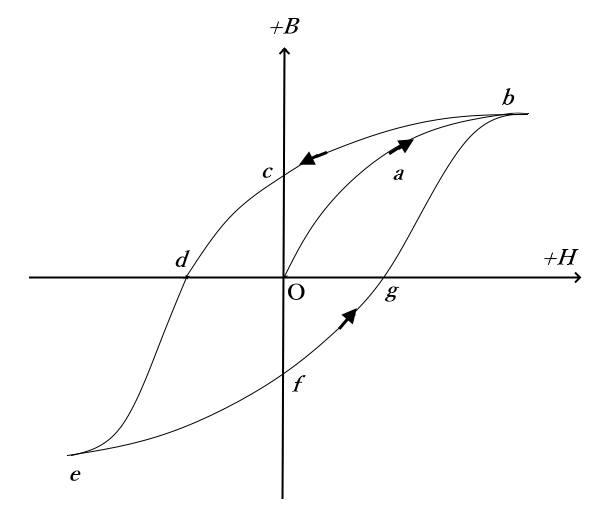
強磁性体に外部から磁界を加えたとき、強磁性体の中にどのような磁束が発生するのかを描いたのを「ヒステリシス曲線」または「磁化曲線」といいます。
O⇒bの経路
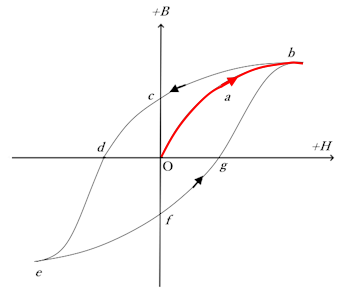
ヒステリシス曲線の原点Oは、強磁性体が磁力を持たず、外部磁界がゼロのときです。
この状態から外部磁界を加えると、強磁性体は磁化していきます。ある一定ラインをすぎると磁化の強さが増加しにくくなります。
そしてb点で磁化の強さが増加しなくなります。この状態のことを「磁気飽和」といいます。
b⇒cの経路

次に、外部磁界を減少させてゼロにして行きます。外部からの磁界がゼロになっても、強磁性体は磁化されています。
c点の高さ $Br$ がその磁化の強さを表しています。これを「残留磁気」または「残留磁束密度」といいます。
この残留磁気が高ければ高いほど、磁石としては強い磁石になります。
c⇒dの経路

外部磁界ゼロの状態から逆向きの磁界を、磁性体の磁化がゼロになるまで加えて行きます。
磁性体の磁化がゼロになったときの外部磁界の強さ $Hc$ を、「保磁力」といいます。
この保磁力が高ければ、永久磁石に向いています。保持力が低ければ、電磁石に向いています。
d⇒e経路

さらに逆向きの磁界を強くして行くと、外部磁界を加えても磁化の強さが増加しないe点に近づいて行きます。
e⇒f⇒g⇒bの経路
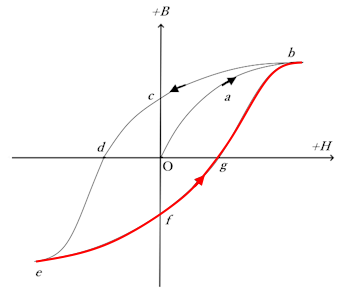
再び外部磁界をはじめの方向に強くして行くと、b⇒c⇒d⇒eと対称な経路をたどります。
理想的な強磁性体では、|og|=|od|、|oc|=|of|となります。
ヒステリシス損
鉄心を磁化すれば、1循環毎にヒステリシス曲線で囲まれた面積に比例したエネルギーの損失が起こります。これをヒステリシス損といいます。ヒステリシス損は鉄心の温度を上げるエネルギーとなります。
磁気遮へい
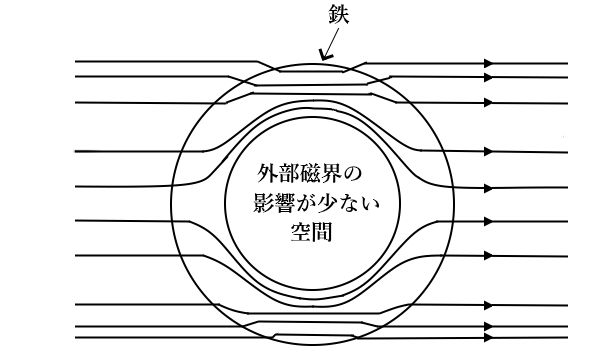
磁界の中に強磁性体でできた中空の鉄球を置くと、磁束は鉄心部分を通過し、中空部分は通過しないといった現象が起きます。これは、磁束が透磁性の高い物質を主に通り、透磁性の高い物質中空部をあまり通らなくなるためです。
この現象を生かして、磁気の影響を受けては困る機器を比透磁率の高い物質で囲み機器を保護しています。これを「磁気遮へい」または、「磁気シールド」といいます。
電験三種-理論の過去問解説:ヒステリシス曲線と損失
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2000年(平成12年)問2【電験理論の過去問題】
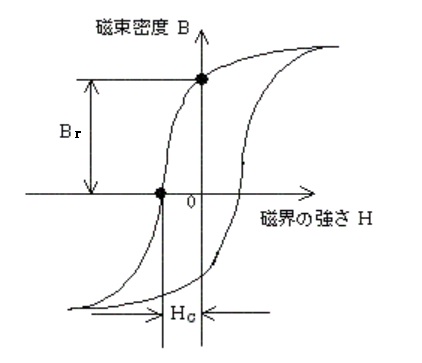
図は強磁性体のヒステリシスループを示す。図中の Br 及び Hc は、それぞれ( ア )及び( イ )の大きさを表す。一般に、$Br$ が大きくて $Hc$ の小さい強磁性体は( ウ )に適し、Br も大きいが、Hc が大きい強磁性体は、( エ )に適する。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)の記入する語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 保磁力 | 磁化力 | 電磁石 | 永久磁石 |
| (2) | 残留磁気 | 保磁力 | 電磁石 | 永久磁石 |
| (3) | 保磁力 | 残留磁束 | 永久磁石 | 電磁石 |
| (4) | 残留磁気 | 保磁力 | 永久磁石 | 電磁石 |
| (5) | 平均磁束密度 | 磁化力 | 電磁石 | 永久磁石 |
ヒステリシスループで磁界の強さがゼロの地点において Br を残留磁気、Hc を保磁力といいます。保磁力が高ければ、永久磁石に向いています。保持力が低ければ、電磁石に向いています。
答え (2)
2006年(平成18年)問3【電験理論の過去問題】
次の文章は、強磁性体の磁化現象について述べたものである。
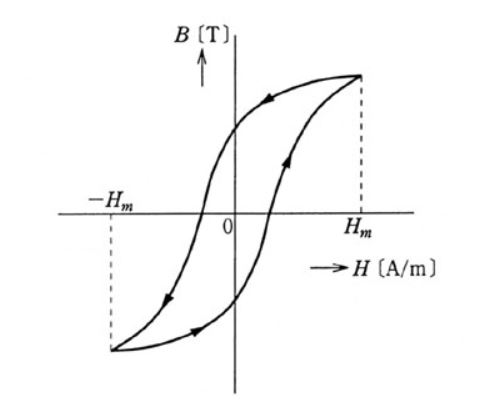
図のように磁界の大きさ $H$[A/m]を $H_m $から $-H_m$ まで変化させた後、再び正の向きに $H_m$ まで変化させると、磁束密度 $B$[T]は一つの閉曲線を描く。この曲線を( ア )という。この曲線を一周りした後では $B$[T]と $H$[A/m]は元の値に戻り、磁化の状態も元の状態に戻る。その間に加えられた単位体積当たりのエネルギー $W_h$[J/㎥]は、この曲線( イ )に等しい。そのエネルギー $W_h$[J/㎥]は強磁性体に与えられるが、最終的には熱の形になって放出される。もし、1秒間に $f$ 回この曲線を描かせると $P$=( ウ )[W/㎥]の電力が熱となる。これを( エ )と名づけている。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に記入する語句又は式として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | ヒステリシス曲線 | の周囲の長さ | $f^2W_k$ | 鉄損 |
| (2) | ヒステリシス曲線 | に囲まれた面積 | $fW_k$ | ヒステリシス損 |
| (3) | ヒステリシス曲線 | に囲まれた面積 | $f^{1.6}W_k$ | ヒステリシス損 |
| (4) | 励磁曲線 | の周囲の長さ | $f^2W_k$ | 渦電流損 |
| (5) | 励磁曲線 | に囲まれた面積 | $fW_k$ | 鉄損 |
ヒステリシス曲線で囲まれた面積に比例したエネルギーの損失が起こります。これをヒステリシス損といいます。ヒステリシス損は鉄心の温度を上げるエネルギーとなります。このとき、$P=fW_k$ の電力が熱になります。
答え (2)
2007年(平成19年)問2【電験理論の過去問題】
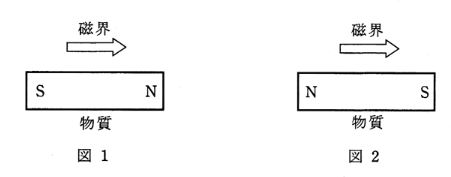
磁界中に物質を置くと、その物質の性質によって図1又は図2に示されるような磁極が現れるものがある。このように物質を磁界中にもってきたために磁気を帯びるようになることを磁化されたといい、この現象を( ア )という。
磁化によって、図1のように磁界と同じ向きの磁束を物質中に生じる磁極が現われる物質の比透磁率は1より大きく、これは( イ )と名付けられている。一方、図2のように磁界と逆向きの磁束を生じる磁極が現れる物質の比透磁率は1より小さく、これは( ウ )といわれる。
特に強く磁化される物質は強磁性体といわれるが、これには( エ )のような物質がある。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 電磁誘導 | 常磁性体 | 反磁性体 | 鉄、ニッケル |
| (2) | 電磁誘導 | 反磁性体 | 常磁性体 | 銅、銀 |
| (3) | 相互誘導 | 常磁性体 | 反磁性体 | 鉄、ニッケル |
| (4) | 磁気誘導 | 常磁性体 | 反磁性体 | 鉄、ニッケル |
| (5) | 磁気誘導 | 反磁性体 | 常磁性体 | 銅、銀 |
磁力を持たない鉄の棒に永久磁石を近づけると、鉄の棒に永久磁石のN極に近い側にS極が現れ、反対側にN極が現れます。これは磁場の向きと同じ方向です。このような現象を「磁気誘導」といいます。
反磁性体は磁化される方向が磁場の向きと逆になるものです。
鉄やニッケル、コバルトなどは外部磁気の影響を強く受けて磁化されます。このような物質を強磁性体といいます。
答え (4)
2015年(平成27年)問3【電験理論の過去問題】
次の文章は、ある強磁性体の初期磁化特性について述べたものである。
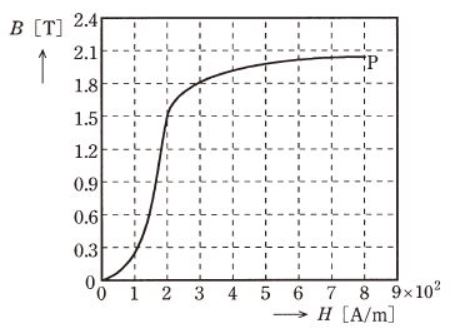
磁界の向きに強く磁化され、比透磁率 $μ_r$ が1よりも非常に( ア )物質を強磁性体という。まだ磁化されていない強磁性体に磁界 $H $[A/m] を加えて磁化していくと、磁束密度 $B$ [T]は図のように変化する。よって、透磁率 $μ$ [H/m](=B/H)も磁界の強さによって変化する。図から、この強磁性体の透磁率 $μ$ の最大値はおよそ $μ_{max}$=( イ )H/mであることが分かる。このとき、強磁性体の比透磁率はほぼ $μ_r$ =( ウ )である。点P以降は磁界に対する磁束密度の増加が次第に緩くなり、磁束密度はほぼ一定の値となる。この現象を( エ )という。
ただし、真空の透磁率を $μ_0=4π×10^{-7} $[H/m]とする。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 大きい | $7.5×10^{-3}$ | $6.0×10^{3}$ | 磁気飽和 |
| (2) | 小さい | $7.5×10^{-3}$ | $9.4×10^{-9}$ | 残留磁気 |
| (3) | 小さい | $1.5×10^{-2}$ | $9.4×10^{-9}$ | 磁気遮へい |
| (4) | 大きい | $7.5×10^{-3}$ | $1.2×10^{4}$ | 磁気飽和 |
| (5) | 大きい | $1.5×10^{-2}$ | $1.2×10^{4}$ | 残留磁気 |
強磁性体の透磁率は真空の透磁率の数百倍以上です。透磁率 $μ=B/H$ ですので、問題の曲線では、その傾きに相当します。
$μ_{max}$ は傾きが最大となる点です。曲線から $H=2×10^2$,$B=1.5$ の点が該当します。
$μ_{max}=\displaystyle \frac{ 1.5 }{ 2×10^2 }=7.5×10^{-3}$
となります。比透磁率 $μ_r$ は、
$μ_r=\displaystyle \frac{ μ_{max}}{μ_0 }=\displaystyle \frac{ 7.5×10^{-3}}{4π×10^{-7} }=6.0×10^3$
となります。磁化の強さが増加しなくなる状態のことを「磁気飽和」といいます。
答え (1)
2016年(平成28年)問4【電験理論の過去問題】
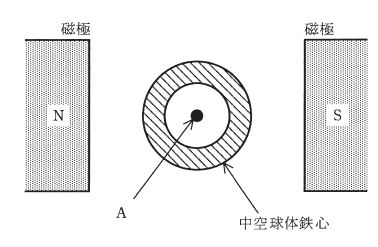
図のように、磁極N、Sの間に中空球体鉄心を置くと、NからSに向かう磁束は、( ア )ようになる。
このとき、球体鉄心の中空部分(内部の空間)の点Aでは、磁束密度は極めて( イ )なる。これを( ウ )という。
ただし、磁極N、Sの間を通る磁束は、中空球体鉄心を置く前と置いた後とで変化しないものとする。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | |
| (1) | 鉄心を避けて通る | 低く | 磁気誘導 |
| (2) | 鉄心中を通る | 低く | 磁気遮へい |
| (3) | 鉄心を避けて通る | 高く | 磁気遮へい |
| (4) | 鉄心中を通る | 低く | 磁気誘導 |
| (5) | 鉄心中を通る | 高く | 磁気誘導 |
磁界の中に強磁性体でできた中空の鉄球を置くと、磁束は鉄心部分を通過し、中空部分は通過しないといった現象が起きます。
この現象を生かして、磁気の影響を受けては困る機器を比透磁率の高い物質で囲み機器を保護しています。これを「磁気遮へい」または、「磁気シールド」といいます。
答え (2)
2017年(平成29年)問4【電験理論の過去問題】
図は、磁性体の磁化曲線(BH曲線)を示す。次の文章は、これに関する記述である。
1 直交座標の横軸は、( ア )である。
2 aは、( イ )の大きさを表す。
3 鉄心入りコイルに交流電流を流すと、ヒステリシス曲線内の面積に( ウ )した電気エネルギーが鉄心の中で熱として失われる。
4 永久磁石材料としては、ヒステリシス曲線のaとbがともに( エ )磁性体が適している。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。


磁化横軸は外部から加える磁界の強さ $H$[A/m]で、縦軸は鉄心内部の磁束密度 $B$[T]を表します。$a$ は、外部の磁界が無くなっても磁気が残りますので残留磁気です。
永久磁石は、残留磁気が大きく容易に消えない必要がありますので、ヒステリシス曲線のaとbがともに大きな磁性体が適します。
答え(5)
電験三種の理論科目に出題される「電磁気分野」のページ
1.磁力線と磁束
2.アンペールの法則
3.フレミングの左手の法則
4.電流が磁界から受ける力
5.ヒステリシス曲線と損失
6.電磁誘導(レンツの法則とファラデーの法則)
7.自己インダクタンス
8.相互インダクタンス
9.磁気エネルギー






