単相交流の並列回路

このページでは、単相交流の並列回路について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題された単相交流の並列回路の過去問題の求め方も解説しています。

$RL$ 並列回路

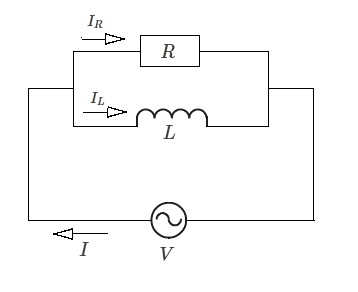
図のように、抵抗 $R$ とコイル $L$ からなる並列回路は、次のような関係式が成り立ちます。

$\dot{I_R}=\displaystyle \frac{ \dot{V} }{ R }$
$\dot{I_L}=\displaystyle \frac{ \dot{V} }{ jωL }=-j\displaystyle \frac{ \dot{V} }{ ωL }
$
$\dot{I}=\dot{I_R}+\dot{I_L}=(\displaystyle \frac{ 1 }{ R }-j\displaystyle \frac{ 1 }{ ωL })\dot{V}$

電流 $V$ を基準としたフェーザ図は次のようになります。

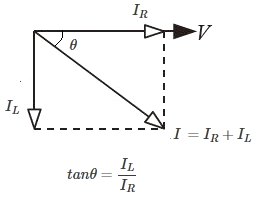
合成インピーダンス $\dot{Z}$ の大きさ $Z$［Ω］と電源電圧 $\dot{V}$，電流 $\dot{I}$ 間の位相差 $θ$ は次のようになります。

$Z=\displaystyle \frac{1}{\sqrt{(\frac{ 1 }{ R })^2+(\frac{ 1 }{ ωL })^2}}=\displaystyle \frac{ωRL}{\sqrt{R^2+(ωL)^2}}$

$θ=tan^{-1}\displaystyle \frac{- \frac{ 1 }{ ωL }}{\frac{ 1 }{ R }}=tan^{-1}(-\displaystyle \frac{R}{ωL})$

$RC$ 並列回路

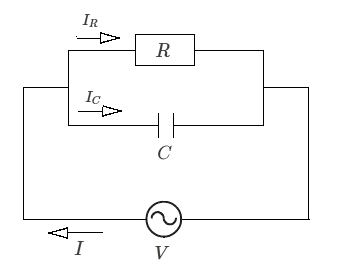
図のように、抵抗 $R$ とコンデンサ $C$ からなる並列回路は、次のような関係式が成り立ちます。

$\dot{I_R}=\displaystyle \frac{ \dot{V} }{ R }$
$\dot{I_C}= jωC\dot{V}$
$\dot{I}=\dot{I_R}+\dot{I_C}=(\displaystyle \frac{ 1 }{ R }+jωC)\dot{V}$

電流 $V$ を基準としたフェーザ図は次のようになります。

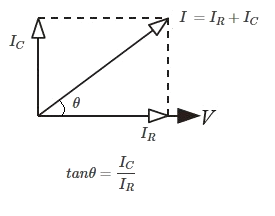
合成インピーダンス $\dot{Z}$ の大きさ $Z$［Ω］と電源電圧 $\dot{V}$，電流 $\dot{I}$ 間の位相差 $θ$ は次のようになります。

$Z=\displaystyle \frac{1}{\sqrt{(\displaystyle \frac{ 1 }{ R })^2+(ωC)^2}}=\displaystyle \frac{R}{\sqrt{1+(ωCR)^2}}$

$θ=tan^{-1}\displaystyle \frac{ωC}{ \frac{ 1 }{ R }}=tan^{-1}ωCR$

$RLC$ 並列回路

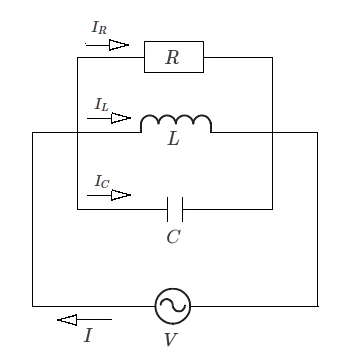
図のように、抵抗 $R$ とコイル $L$ ，コンデンサ $C$ からなる並列回路は、次のような関係式が成り立ちます。

$\dot{I_R}=\displaystyle \frac{ \dot{V} }{ R }$
$\dot{I_L}=\displaystyle \frac{ \dot{V} }{ jωL }=-j\displaystyle \frac{ \dot{V} }{ ωL }
$
$\dot{I_C}= jωC\dot{V}$
$\dot{I}=\dot{I_R}+\dot{I_L}+\dot{I_C}=\{\displaystyle \frac{ 1 }{ R }+j(ωC-\displaystyle \frac{ 1 }{ ωL })\}\dot{V}$

電流 $V$ を基準にしたフェーザ図は次のようになります。

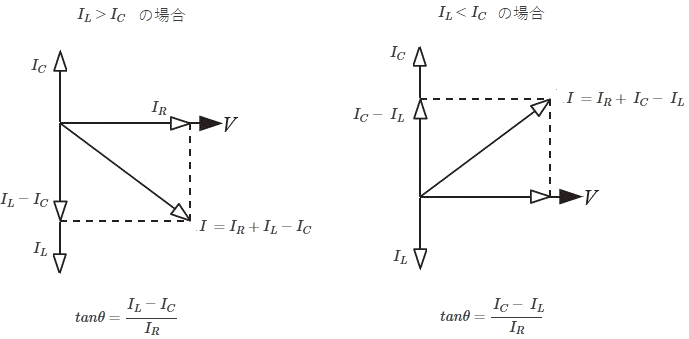
合成インピーダンス $\dot{Z}$ の大きさ $Z$［Ω］と電源電圧 $\dot{V}$，電流 $\dot{I}$ 間の位相差 $θ$ は次のようになります。

$Z=\displaystyle \frac{1}{\sqrt{(\frac{1}{R})^2+(ωC- \frac{ 1 }{ ωL })^2}}$

$θ=tan^{-1}(\displaystyle \frac{ωC-\frac{1}{ωL}}{\frac{1}{R}})$

　　

電験三種－理論（交流回路）過去問題

1997年（平成9年）問7

図のような交流回路において、抵抗 $R$ の流れる電流 $I_R$［A］の大きさはいくらか。正しい値を次のうちから選べ。

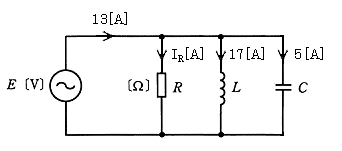
(1) 5　(2) 6　(3) 7　(4) 8　(5) 9

1997年（平成9年）問7　過去問解説

電圧と電流の関係を図で示します。

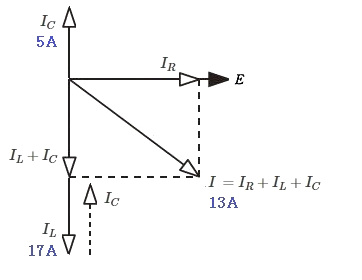
図より

$\begin{eqnarray} I&=&\sqrt{{I_R}^2+(I_L-I_C)^2}\\\\&=&\sqrt{{I_R}^2+(17-5)^2}\\\\&=&\sqrt{{I_R}^2+12^2}=13\end{eqnarray} $

${I_R}^2+12^2=13^2$

${I_R}=\sqrt{13^2-12^2}=5$［A］

答え (1)

1999年（平成11年）問11

図のような交流回路において $12$［Ω］の抵抗に $5$［A］の電流が流れた。誘導リアクタンス $X_L$［Ω］の値として、正しい値は次のうちどれか。

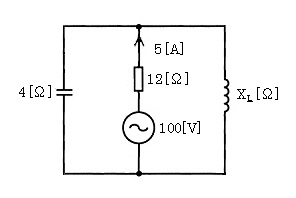
(1) 3.2　(2) 5.3　(3) 8.0　(4) 12　(5) 16

1999年（平成11年）問11　過去問解説

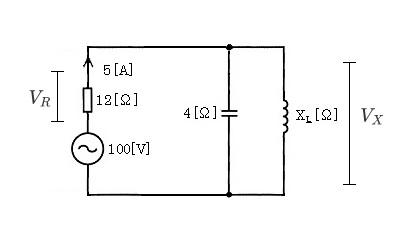
抵抗部分の電圧を $V_R$［V］とすると、並列部分になっているリアクタンス部分の電圧 $V_X$［V］は、

$V_X=\sqrt{V-V_R}=\sqrt{100^2-(5×12)^2}=80$［V］

コンデンサに流れる電流を $I_C$［A］とすると、

$I_C=\displaystyle \frac{V_X}{X_C}=20$［A］

$|I_L-I_C|=5$［A］になるのは、$I_L=15$ と $25$［A］の二つの場合が考えられます。

$I_L=15$［A］の場合

$X_L=\displaystyle \frac{80}{15}=5.3$［Ω］

$I_L=25$［A］の場合

$X_L=\displaystyle \frac{80}{25}=3.2$［Ω］

答え (1)または(2)

2000年（平成12年）問11

図のような回路において、抵抗 $R_2$ に流れる電流 $\dot{I_2}$［A］の値が $5$［A］であるとき、次の(a)及び(b)に答えよ。

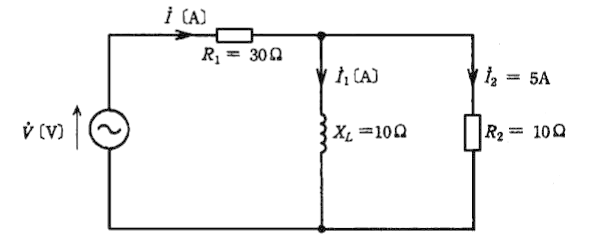
(a) 抵抗 $R_1$ に流れる電流 $\dot{I}$［A］の値として、正しいは次のうちどれか。ただし、$\dot{I_2}$ を基準ベクトルとする。

(1) $5+j5$　(2) $5-j5$　(3) $10+j5$　(4) $10+j10$　(5) $10-j10$

(b) この回路の電源電圧 $\dot{V}$ の絶対値 $V$［V］の値として、正しいのは次のうちどれか。

(1) 100　(2) 150　(3) 200　(4) 250　(5) 350

2000年（平成12年）問11　過去問解説

(a) 抵抗 $R_2$ の電圧を $\dot{V_2}$［V］とすると、

$\dot{V_2}=R_2\dot{I_2}=10×5＝50$［V］

$V_2$［V］は、リアクタンス $X_L$ に加わる電圧と同じですので、$\dot{I_1}$［A］は、

$\dot{I_1}=\displaystyle \frac{50}{jX_L}=\displaystyle \frac{50}{j10}=-j5$［A］

電流 $\dot{I}$［A］は、

$\dot{I}=\dot{I_1}+\dot{I_2}=5-j5$［A］

答え (2)

(b) 抵抗 $R_1$ の電圧を $\dot{V_1}$［V］とすると、

$\dot{V_1}=R_1\dot{I_1}=30(5-j5)＝150-j150$［V］

電源電圧 $\dot{V}$［Ｖ］は、

$\dot{V}=\dot{V_1}+\dot{V_2}=(150-j150)+50=200-j150$

したがって、$|V|$［V］は、

$|V|=\sqrt{200^2+150^2}=250$［V］

答え (4)

2003年（平成15年）問8

図１のように、$R$［Ω］の抵抗、インダクタンス $L$［H］のコイル及び静電容量 $C$［F］のコンデンサを並列に接続した回路がある。この回路に正弦波交流電圧 $e$［V］を加えたとき、この回路の各素子に流れる電流 $i_R$［A］、$i_L$［A］、$i_C$［A］と $e$［V］の時間変化はそれぞれ図２のようで、それぞれの電流の波高値は $10$［A］、$15$［A］、$5$［A］であった。回路に流れる電流 $i$［A］の電圧 $e$［V］に対する位相として、正しいのは次のうちどれか。

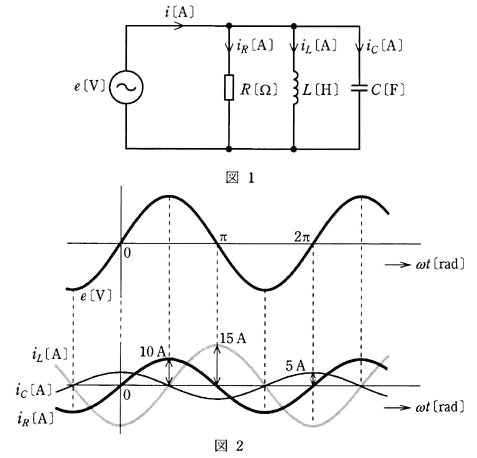
(1) 30°遅れる　(2) 30°進む　(3) 45°遅れる　(4) 45°進む　(5) 90°遅れる

2003年（平成15年）問8　過去問解説

電圧と電流の関係を図で示します。

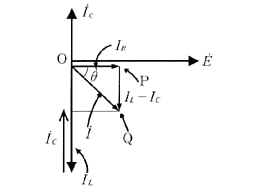
位相差を $θ$ とすると、

$tanθ=\displaystyle \frac{I_L-I_C}{I_R}=\displaystyle \frac{\frac{15}{\sqrt{2}}-\frac{5}{\sqrt{2}}}{\frac{10}{\sqrt{2}}}=1$

$θ=45$°の遅れとなります。

答え (3)

2003年（平成15年）問14

図は、破線で囲んだ未知のコイルのインダクタンス $L_x$［H］と抵抗 $R_x$［Ω］を測定するために使用する交流ブリッジ(マクスウェルブリッジ)の等価回路である。このブリッジが平衡した場合のインダクタンス $L_x$[H]と $R_x$［Ω］の値として、正しいものを組み合わせたのは次のうちどれか。
　ただし、交流ブリッジが平衡したときの抵抗器の値は $R_p$［Ω］、$R_q$［Ω］、標準コイルのインダクタンスと抵抗の値はそれぞれ $L_s$［H］、$R_s$［Ω］とする。

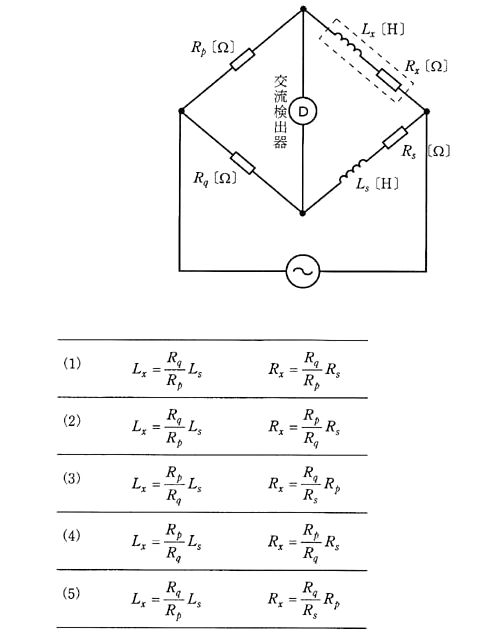
2003年（平成15年）問14　過去問解説

ブリッジ回路の平衡条件より

$R_p(R_s+jωL_s)=R_q(R_x+jωL_x)$

$R_pR_s+jωR_pL_s=R_qR_x+jωR_qL_x$

$R_pR_s=R_qR_x$ より

$R_x=\displaystyle \frac{R_pR_s}{R_q}$

$jωR_pL_s=jωR_qL_x$ より

$L_x=\displaystyle \frac{R_pL_s}{R_q}$

答え (4)

2007年（平成19年）問9

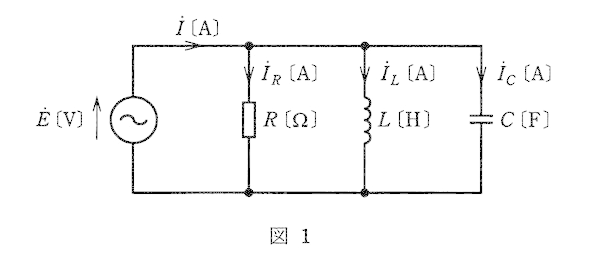
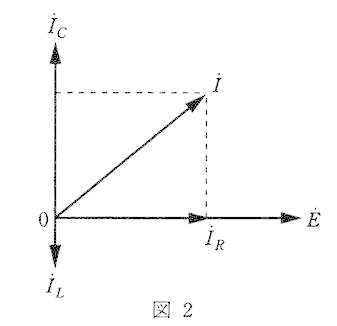
図1に示す、$R$［Ω］の抵抗、インダクタンス $L$［H］のコイル、静電容量 $C$［F］のコンデンサからなる並列回路がある。この回路に角周波数 $ω$［rad/s］の交流電圧 $\dot{E}$［V］を加えたところ、この回路に流れる電流 $\dot{I}$［A］、$\dot{I_R}$［A］、$\dot{I_L}$［A］、$\dot{I_C}$［A］のベクトル図が図2に示すようになった。このときの $L$ と$C$ の関係を表す式として、正しいのは次のうちどれか。

(1) $ωL<\displaystyle\frac{1}{ωC}$　(2) $ωL>\displaystyle\frac{1}{ωC}$　(2) $ω^2=\displaystyle\frac{1}{\sqrt{LC}}$　(4) $ωL=\displaystyle\frac{1}{ωC}$　(5) $R=\sqrt{\displaystyle\frac{L}{C}}$　

2007年（平成19年）問9　過去問解説

ベクトル図より

$I_L<I_C$

$X_L>X_C$

$ωL>\displaystyle \frac{1}{ωC}$

答え (2)

2009年（平成21年）問7

図のように抵抗、コイル、コンデンサからなる負荷がある。この負荷に線間電圧 $\dot{V}_{ab}=100∠0°$［V］，$\dot{V}_{bc}=100∠0°$［V］，$\dot{V}_{ac}=200∠0°$［V］の単相３線式交流電源を接続したところ、端子 a，端子 b，端子 c を流れる線電流はそれぞれ $\dot{I}_a$［A］，$\dot{I}_b$［A］及び $\dot{I}_c$［A］であった。$\dot{I}_a$［A］，$\dot{I}_b$［A］，$\dot{I}_c$［A］の大きさをそれぞれ $I_a$［A］，$I_b$［A］ ，$I_c$［A］としたとき，これらの大小関係を表す式をして，正しいのは次のうちどれか。

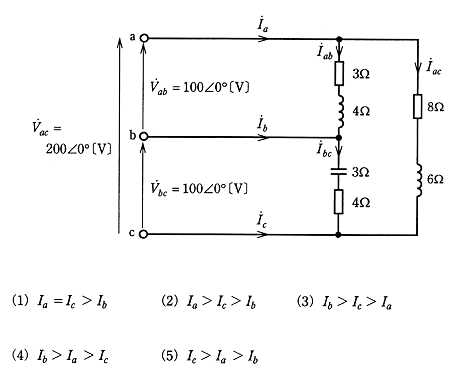
2009年（平成21年）問7　過去問解説

問題の図より $I_{ab}$［A］，$I_{bc}$［A］，$I_{ac}$［A］は、

$\begin{eqnarray}\dot{I}_{ab}&=&\displaystyle \frac{\dot{V}_{ab}}{3+j4}\\\\&=&\displaystyle \frac{100}{3+j4}\\\\&=&\displaystyle \frac{100(3-j4)}{(3+j4)(3-j4)}\\\\&=&\displaystyle \frac{100}{25}(3-j4)=12-j16［A］\end{eqnarray}$

$\begin{eqnarray}\dot{I}_{bc}&=&\displaystyle \frac{\dot{V}_{bc}}{4-j3}\\\\&=&\displaystyle \frac{100}{4-j3}\\\\&=&\displaystyle \frac{100(4+j3)}{(4-j3)(4+j3)}\\\\&=&\displaystyle \frac{100}{25}(4+j3)=16+j12［A］\end{eqnarray}$

$\begin{eqnarray}\dot{I}_{ac}&=&\displaystyle \frac{\dot{V}_{ac}}{8+j6}\\\\&=&\displaystyle \frac{200}{8+j6}\\\\&=&\displaystyle \frac{200(8-j6)}{(8+j6)(8-j6)}\\\\&=&\displaystyle \frac{200}{100}(8-j6)=16-j12［A］\end{eqnarray}$

$\dot{I}_a$［A］，$\dot{I}_b$［A］，$\dot{I}_c$［A］とその大きさ $I_a$［A］，$I_b$［A］ ，$I_c$［A］は、

$\begin{eqnarray}\dot{I}_a&=&\dot{I}_{ab}+\dot{I}_{ac}\\\\&=&(12-j16)+(16-j12)=28-j28［A］\end{eqnarray}$

$I_a=\sqrt{28^2+28^2}=28\sqrt{2}≒39.6［A］$

$\begin{eqnarray}\dot{I}_b&=&\dot{I}_{bc}-\dot{I}_{ab}\\\\&=&(16+j12)-(12-j16)=4+j28［A］\end{eqnarray}$

$I_b=\sqrt{4^2+28^2}≒28.3［A］$

$\begin{eqnarray}\dot{I}_c&=&-(\dot{I}_{bc}+\dot{I}_{ac})\\\\&=&-\{(16+j12)+(16-j12)\}=-32［A］\end{eqnarray}$

$I_c=32［A］$

したがって、$I_a>I_c>I_b$ になります。

答え (2)

2012年（平成24年）問10

図のように、$R_1=20$［Ω］と $R_2=30$［Ω］の抵抗、静電容量 $C=\displaystyle \frac{1}{100π}$［F］のコンデンサ、インダクタンス $L=\displaystyle \frac{1}{4π}$［H］のコイルからなる回路に周波数 $f$ ［Hz］で実効値 $V$［V］が一定の交流電圧を加えた。$f=10$［Hz］のときに $R_1$ を流れる電流の大きさを $I_{10Hz}$［A］、$f=10$［MHz］のときに $R_1$ を流れる電流の大きさを $I_{10MHz}$［A］とする。このとき、電流比 $L=\displaystyle \frac{I_{10Hz}}{I_{10MHz}}$ の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

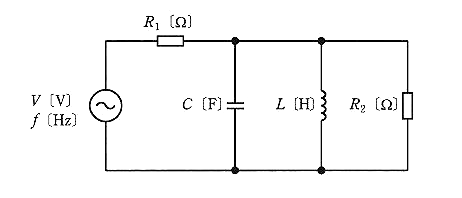
(1) 0.4　(2) 0.6　(3) 1.0　(4) 1.7　(5) 2.5

2012年（平成24年）問10　過去問解説

$f=10$［Hz］のときの回路の合成インピーダンスを $\dot{Z}_{10Hz}$ ［Ω］とすると、

$\begin{eqnarray}\dot{Z}_{10Hz}&=&R_1+\displaystyle \frac{1}{\displaystyle \frac{1}{R_2}+\displaystyle \frac{1}{j2πfL}+j2πfC}\\\\&=&20+\displaystyle \frac{1}{\displaystyle \frac{1}{30}+\displaystyle \frac{1}{j2π･10･\displaystyle \frac{1}{4π}}+j2π･10･\displaystyle \frac{1}{100π}}\\\\&=&20+\displaystyle \frac{1}{\displaystyle \frac{1}{30}-j\displaystyle \frac{1}{5}+j\displaystyle \frac{1}{5}}=50［Ω］\end{eqnarray}$

$R_1$ を流れる電流の大きさを $I_{10Hz}$［A］は、

$I_{10Hz}=\displaystyle \frac{V}{\dot{Z}_{10Hz}}=\displaystyle \frac{V}{50}［A］$

$f=10$［MHz］のときの回路の合成インピーダンスを $\dot{Z}_{10MHz}$ ［Ω］とすると、

$\begin{eqnarray}\dot{Z}_{10MHz}&=&R_1+\displaystyle \frac{1}{\displaystyle \frac{1}{R_2}+\displaystyle \frac{1}{j2πfL}+j2πfC}\\\\&=&20+\displaystyle \frac{1}{\displaystyle \frac{1}{30}+\displaystyle \frac{1}{j2π･10･10^6･\displaystyle \frac{1}{4π}}+j2π･10･10^6･\displaystyle \frac{1}{100π}}\\\\&=&20+\displaystyle \frac{1}{\displaystyle \frac{1}{30}-j2･10^{-7}+j2･10^5}≒20［Ω］\end{eqnarray}$

$R_1$ を流れる電流の大きさを $I_{10MHz}$［A］は、

$I_{10MHz}=\displaystyle \frac{V}{\dot{Z}_{10MHz}}=\displaystyle \frac{V}{20}［A］$

したがって、電流比 $L=\displaystyle \frac{I_{10Hz}}{I_{10MHz}}$ は、

$L=\displaystyle \frac{\displaystyle \frac{V}{50}}{\displaystyle \frac{V}{20}}＝0.4$

答え (1)

2013年（平成25年）問9

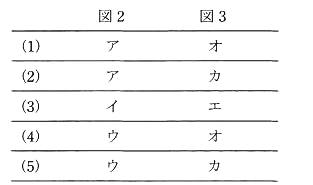
図１のように、$R$［Ω］の抵抗、インダクタンス $L$［H］のコイル、静電容量 $C$［F］のコンデンサからなる並列回路がある。この回路に角周波数 $ω$［rad/s］の交流電圧 $v$［V］を加えたところ、この回路に流れる電流は $i$［A］であった。電圧 $v$［V］及び電流 $i$［A］のベクトルをそれぞれ電圧 $\dot{V}$［V］と電流 $\dot{I}$［A］とした場合、両ベクトルの関係を示す図２（ア、イ、ウ）及び $v$［V］と $i$［A］の時間 $t$［ｓ］の経過による変化を示す図３（エ、オ、カ）の組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。
ただし、$R≫ωL$ 及び　$ωL=\displaystyle \frac{2}{ωC}$ とし、一切の過渡現象は無視するものとする。

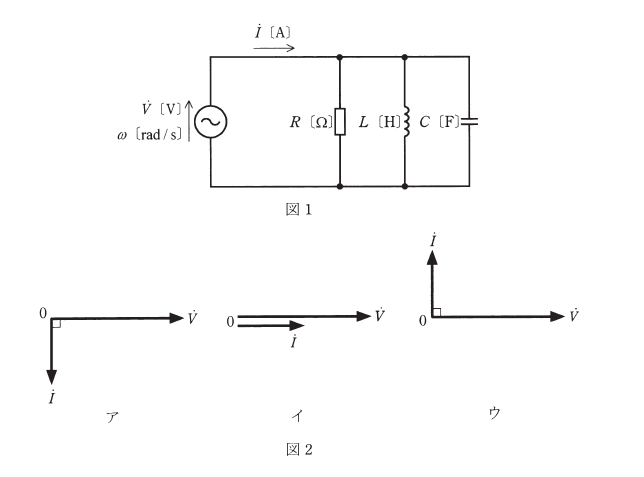
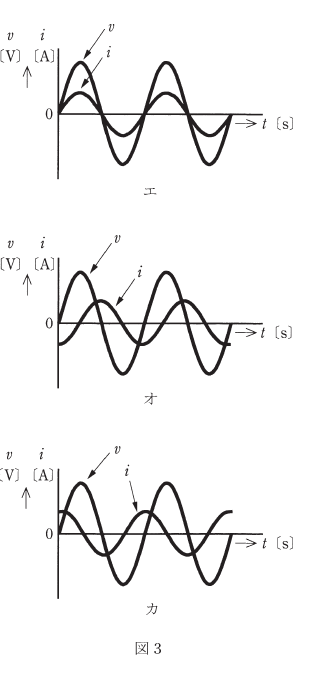
2013年（平成25年）問9　過去問解説

コイル $L$ に流れる電流を $I_L$［A］、コンデンサ $C$ に流れる電流を $L_C$［A］とすると、

$I_L=\displaystyle \frac{V}{ωL}$［A］

$I_C=ωCV$［A］

$ωL=\displaystyle \frac{2}{ωC}$ なので、

$I_C=ωCV=\displaystyle \frac{2V}{ωL}=2I_L$［A］

コンデンサに流れる電流の方が大きいので、回路全体として容量性になります。また、$R≫ωL$ なので、抵抗分は無視できます。したがって、電流は電圧より 90°進みます。これらを満たす解答は(5)となります。

答え (5)

2017年（平成29年）問15

図は未知のインピーダンス $\dot{Z}$［Ω］を測定するための交流ブリッジである。電源の電圧を $\dot{E}$［V］、角周波数を $ω$［rad/s］とする。ただし $ω$，静電容量 $C_1$［F］，抵抗$R_1$［Ω］，$R_2$［Ω］，$R_3$［Ω］は零でないとする。次の(a)及び(b)の問に答えよ。

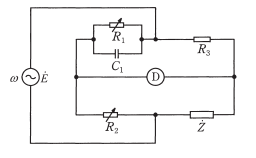
(a)　交流検出器Dによる検出電圧が零となる平衡条件を $\dot{Z}$，$R_1$，$R_2$，$R_3$，$ω$ 及び $C_1$ を用いて表すと、

$(　　　　　)\dot{Z}=R_2R_3$

上式の空白に入る式として適切なものを次の(1)～(5)のうちから一つ選べ。

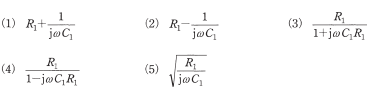
（b）$\dot{Z}=R+jX$ としたとき、この交流ブリッジで測定できる $R$［Ω］と $X$［Ω］の満たす条件として、正しいものを次の(1)～(5)のうちから一つ選べ。

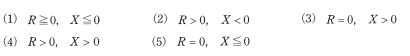
2017年（平成29年）問15　過去問解説

(a)　ブリッジ回路の平衡条件より、空白に入る式は、$R_1$ と $C_1$ の合成インピーダンス $\dot{Z_１}$［Ω］になりますので、

$\dot{Z_１}=\displaystyle\frac{R_1×(-j\displaystyle\frac{1}{ωC_1})}{R_1-j\displaystyle\frac{1}{ωC_1}}=\displaystyle\frac{\displaystyle\frac{R_1}{jωC_1}}{R_1+\displaystyle\frac{1}{jωC_1}}=\displaystyle\frac{R_1}{1+jωR_1C_1}$

答え（2）

(b)　式を $\dot{Z}=R+jX$ に変形します。

$\displaystyle\frac{R_1}{1+jωR_1C_1}\dot{Z}=R_2R_3$

$\dot{Z}=\displaystyle\frac{R_2R_3}{R_1}(1+jωR_1C_1)$

$\dot{Z}=\displaystyle\frac{R_2R_3}{R_1}+jωR_2R_3C_1$

と変形できますので、$R=\displaystyle\frac{R_2R_3}{R_1}$，$X=ωR_2R_3C_1$ に対応します。問題文より、$ω$，静電容量 $C_1$［F］，抵抗$R_1$［Ω］，$R_2$［Ω］，$R_3$［Ω］は零でないとありますので、$R>0$，$X>0$ となります。

答え（4）