フレミングの左手の法則

このページでは、フレミングの左手の法則について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題されたフレミングの左手の法則の過去問題も解説しています。

フレミングの左手の法則
電流が磁界から受ける力の大きさ
電験三種－理論（電磁気）過去問

フレミングの左手の法則

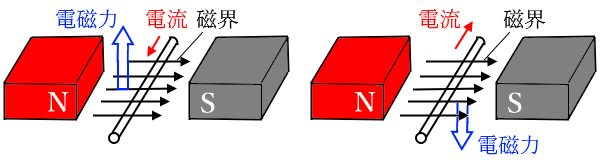
導体に電流を流すと磁界が発生します。電流を流した導体を永久磁石の磁界が及ぼす範囲中に置けば、電流が作る磁界と磁石が作る磁界との相互作用で力が発生します。この力を「電磁力」といいます。

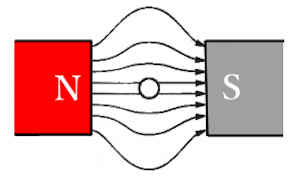
導線に電流が流れていない時は、導線は磁界の影響を受けません。

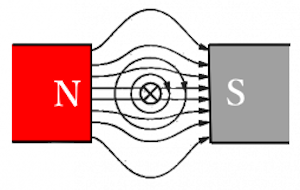
導線に電流を流すと、導線のまわりに磁界が発生します。

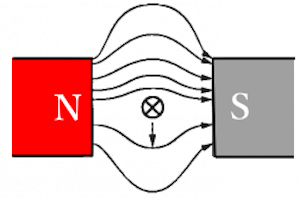
磁力線の相互作用により、導線の上側では磁力線が密になり、導線の下側では磁力線が疎になります。磁力線がゴムのようにはたらき、導線は下向きに力を受けます。

このように電流が流れている導線が磁界から受ける力を電磁力といいます。このように磁力線で考えると電線にどの向きに力が加わるのかを知ることができます。ただ、磁力線を描くのは面倒です。そこで、「電流」、「磁石による磁界」、「受ける力」、のそれぞれの方向を簡単に知る方法があります。

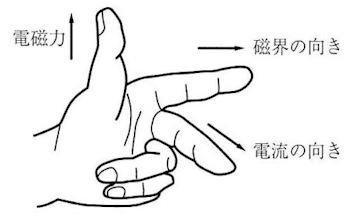
フレミング左手の法則は、左手の三本の指に当てはめて方向を考えます。

中指から順番に「電・磁・力」です。親指がいちばん力が入るので「力」と覚えます。

電流が磁界から受ける力の大きさ

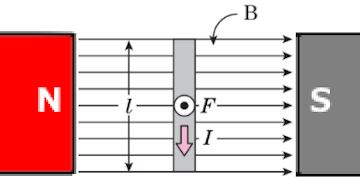
磁束密度 $B$［Ｔ］の一様な磁界のなかに、磁界と直角に長さ $l$［m］の導体を置いて、電流 $I$［A］流した時の導線が受ける電磁力の大きさ $F$［N］は次の式で求められます。

$F=BIl=μHIl$［N］

また、導体と磁界の方向が $θ$傾いているときの電磁力の大きさは、次のようになります。

$F=BIlsinθ=μHIlsinθ$［N］

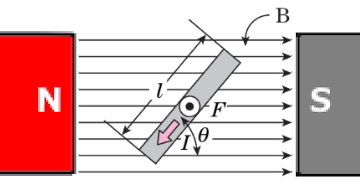
磁界の方向と導線とが垂直のときは力が最大になります。

導体と磁界の方向が $θ$ 傾いているときの電磁力の大きさを求める問題で、$θ$ の使い方は非常に間違いやすいです。注意してください。

電験三種－理論（電磁気）過去問

(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。

1998年（平成10年）問3

図のように磁束密度 $B=0.5$［T］の一様な磁界の中に直線状の導体を磁界の方向に対して $30°$の角度におき、これに $I=100$［A］の直流電流を流した。このとき、導体の単位長さ当たりに働く力 $F$［N/m］の値として、正しいのは次のうちどれか。

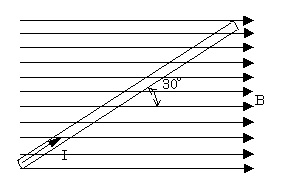
(1) 10　(2) 25　(3) 38　(4) 46　(5) 53

1998年（平成10年）問3　過去問解説

導体と磁界の方向が $θ$ 傾いているときの電磁力の大きさ $F$［Ｎ］は、

$F=BIlsinθ=0.5×100×1×sin30°=25$［N］

答え (2)

2011年（平成23年）問3

電流が流れている長さ $L$［m］の直線導体を磁束密度が一様な磁界中に置くと、フレミングの（　ア　）の法則に従い、導体には電流の向きにも磁界の向きにも直角な電磁力が働く。直線導体の方向を変化させて、電流の方向が磁界の方向と同じになれば、導体に働く力の大きさは（　イ　）となり、直角になれば、（　ウ　）となる。力の大きさは、電流の（　エ　）に比例する。

上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる組合わせとして、正しいものを次の(1)～(5)のうちから一つ選べ。