第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「電磁誘導(レンツの法則とファラデーの法則)」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「電磁誘導(レンツの法則とファラデーの法則)」の過去問題も解説しています。
レンツの法則とファラデーの法則
コイルに電流を流せば、磁界が発生します。その逆として、コイルの中の磁界を変化させると電流が流れます。コイルと磁石を近づけたり遠ざけたりすると、コイルに電流が流れるということです。この現象を「電磁誘導」といいます。また、発生した電圧を「誘導起電力」、流れた電流を「誘導電流」といいます。
レンツの法則
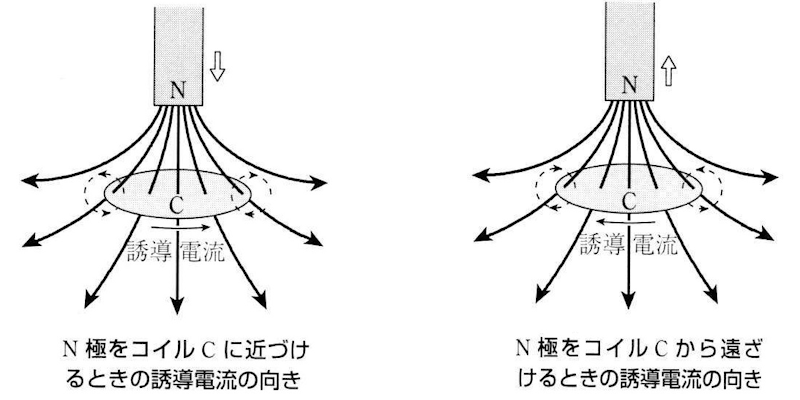
コイルCにN極を近づけると、コイルを貫く下向きの磁束が増加します。このとき誘導電流による磁界が上向きになるように誘導電流が流れます。
N極をコイルから遠ざけると、コイルを貫く下向きの磁束が減少します。このとき誘導電流による磁界が下向きになるように誘導電流が流れます。
このように、誘導起電力によってコイルに流れる誘導電流が作る磁束は、元の磁束の変化を妨げる方向になります。コイルは磁石が近づいてくると反発し、遠ざかると引き付ける方向です。この法則を「レンツの法則」といいます。
ファラデーの電磁誘導の法則
コイルを貫く磁束量 $ϕ$ が変化すると、電磁誘導により誘導起電力 $V$ が発生します。そのときの誘導起電力は、「ファラデーの電磁誘導の法則」で求めることができます。
ファラデーの電磁誘導の法則
時間 $Δt$[s]の間に、コイルを貫く磁束が $Δϕ$[Wb]だけ変化するとき、$N$ 巻きのコイルに発生する誘導起電力 $e $[V]は、次のように表されます。
$e=-N\displaystyle\frac{Δϕ}{Δt}$
$e$[V]:コイルに発生する誘導起電力
$N$:コイルの巻数
$Δφ$[Wb]:変化した磁束の量
$Δt$[秒]:磁束が変化するのに要した時間
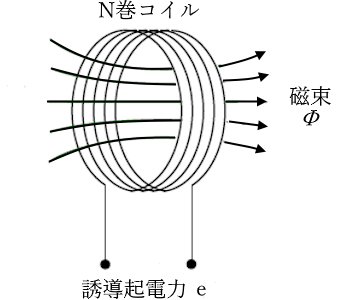
マイナスがつくのは、レンツの法則で磁束の変化を妨げる方向だからです。
電磁誘導の法則は
- 磁石を速く動かすほど
- 磁石の磁力が強いほど
- コイルの巻き数が多いほど
発生する誘導起電力は大きくなります。電磁誘導は発電の原理となっています。
磁界を横切る導体に生じる誘導起電力
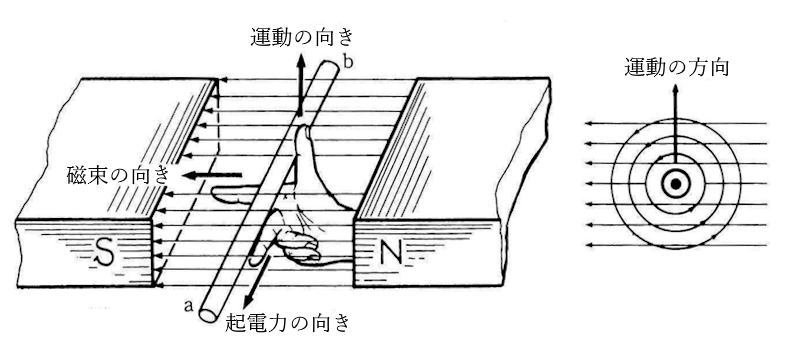
磁界中において導体を移動させると、導体に誘導起電力が発生します。このときの導体の移動方向(運動の向き)、
磁束(磁界)の向き、誘導起電力の向きを、右手を使ってあらわした法則を「フレミング右手の法則」といいます。
フレミングの右手の法則を使うと「起電力(中指)」「磁石による磁界の向き(人差し指)」「運動の向き(親指)」のそれぞれの方向を簡単に知ることができます。
フレミングの左手は電動機、右手は発電機の原理です。混同しないようにしてください。
磁界を横切る導体に生じる誘導起電力
導体が移動する空間の磁束密度を $B$[T]、導体の長さを $l$[m]、導体の移動速度を $v$[m/s]、磁力線と移動方向の角度を $θ$ とすると、誘導される起電力の大きさ $V$[V]は、次のように表されます。
$\begin{eqnarray}V&=&-\displaystyle\frac{Δϕ}{Δt}\\\\&=&-\displaystyle\frac{B×l×v×Δt×sinθ}{Δt}\\\\&=&-Blvsinθ[V]\end{eqnarray}$
電験三種-理論の過去問解説:電磁誘導(レンツの法則とファラデーの法則)
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1997年(平成9年)問2【電験理論の過去問題】
巻数 30 のコイルを貫通している磁束が 0.1 秒間に 1[Wb]の割合で変化するとき、コイルに発生する起電力[V]の大きさはいくらか。正しい値を次のうちから選べ。
(1) 250 (2) 300 (3) 350 (4) 400 (5) 450
誘導起電力 $|V| $[V]は
$V=N\displaystyle\frac{Δϕ}{Δt}=30\displaystyle\frac{1}{0.1}=300$[V]
答え (3)
2001年(平成13年)問1【電験理論の過去問題】
磁束密度 2[T]の平等磁界が一様に紙面の上から下へ垂直に加わっており、長さ 2[m]の直線導体が磁界の方向と直角に置かれている。この導体を図のように 5[m/s]の速度で紙面と平行に移動させたとき、導体に発生する誘導起電力[V]の大きさとして、正しいのは次のうちどれか。
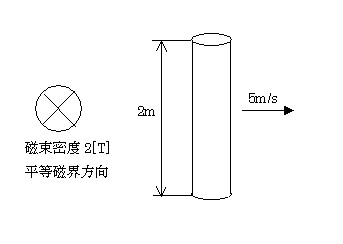
(1) 5 (2) 10 (3) 16 (4) 20 (5) 50
誘導される起電力の大きさ $V$[V]は、
$V=Blvsinθ=2×2×5×1=20$[V]
答え (4)
2004年(平成16年)問3【電験理論の過去問題】
図1のように磁束密度 $B=0.02$[T]の一様な磁界の中に長さ 0.5[m]の直線状導体が磁界の方向と直角に置かれている。図2のようにこの導体が磁界と直角を維持しつつ磁界に対して 60°の角度で、矢印の方向に 0.5[m/s]の速さで移動しているとき、導体に生じる誘導起電力 $e$[mV]の値として、最も近いのは次のうちどれか。
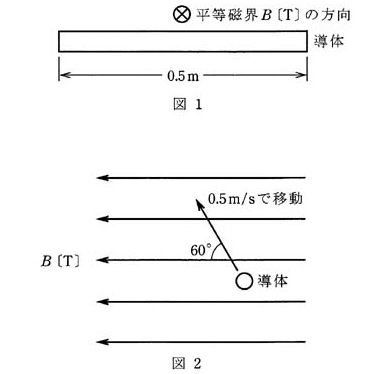
(1) 2.5 (2) 3.0 (3) 4.3 (4) 5.0 (5) 8.6
誘導される起電力の大きさ $V$[V]は、
$\begin{eqnarray}V&=&Blvsinθ\\\\&=&0.02×0.5×0.5×sin60\\\\&=&4.3[mV]\end{eqnarray}$
答え (3)
2010年(平成22年)問3【電験理論の過去問題】
紙面に平行な水平面内において、0.6[m]の間隔で張られた 2 本の直線状の平行導線に 10[Ω]の抵抗が接続されている。この平行導線に垂直に、図に示すように、直線状の導体棒 PQ を渡し、紙面の裏側から表側に向かって磁束密度 $B=6×10^{-2}$[T]の一様な磁界をかける。ここで、導体棒 PQ を磁界と導体棒に共に垂直な矢印の方向に一定の速さ $v=4$[m/s]で平行導線上を移動させているときに、10[Ω]の抵抗に流れる電流 $I$[A]の値として、正しいのは次のうちどれか。
ただし、電流の向きは図に示す矢印の向きを正とする。また、導線及び導体棒 PQ の抵抗、並びに導線と導体棒との接触抵抗は無視できるものとする。
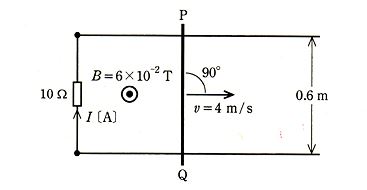
(1) -0.0278 (2) -0.0134 (3) -0.0072 (4) 0.0144 (5) 0.0288
誘導される起電力の大きさ $V$[V]は、
$\begin{eqnarray}V&=&Blvsinθ\\\\&=&6×10^{-2}×0.6×4×sin90\\\\&=&0.144[V]\end{eqnarray}$
抵抗に流れる電流 $I $[A]は、
$I=\displaystyle\frac{V}{R}=\displaystyle\frac{0.144}{10}=0.0144$
答え (4)
2015年(平成27年)問5【電験理論の過去問題】
十分長いソレノイド及び小さい三角形のループがある。図1はソレノイドの横断面を示しており、三角形ループも同じ面内にある。図2はその破線部分の拡大図である。面 $x=0$ から右側の領域( $x>0$ の領域)は直流電流を流したソレノイドの内側であり、そこには $+z$ 方向の平等磁界が存在するとする。その磁束密度を $B$[T]( $B>0$ )とする。
一方、左側領域( $x<0$ )はソレノイドの外側であり磁界は零であるとする。ここで、三角形PQRの抵抗器付き導体ループが $xy$ 平面内を等速度 $u$[m/s]で、$+x$ 方向に進み、ソレノイドの巻線の隙間から内側に侵入していく。その際、導体ループの辺QRは $y$ 軸と平行を保っている。頂点Pが面 $x=0$ を通過する時刻を $T$[s]とする。また、抵抗器の抵抗 $r$[Ω]は十分大きいものとする。
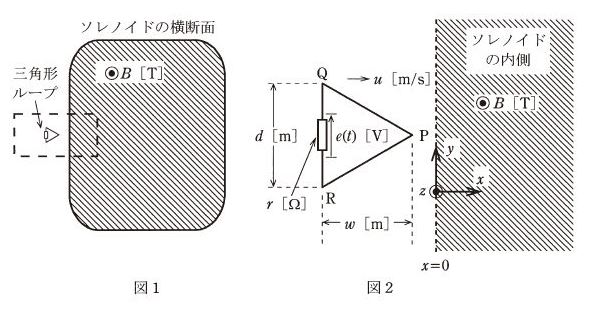
辺QRの中央の抵抗器に時刻 $t$[s]に加わる誘導電圧を $e(t)$[V]とし、その符号は図中の矢印の向きを正と定義する。三角形ループがソレノイドの外側から内側に入り込むときの $e(t)$ を示す図として、最も近いものを次の(1)~(5)のうちから一つ選べ。
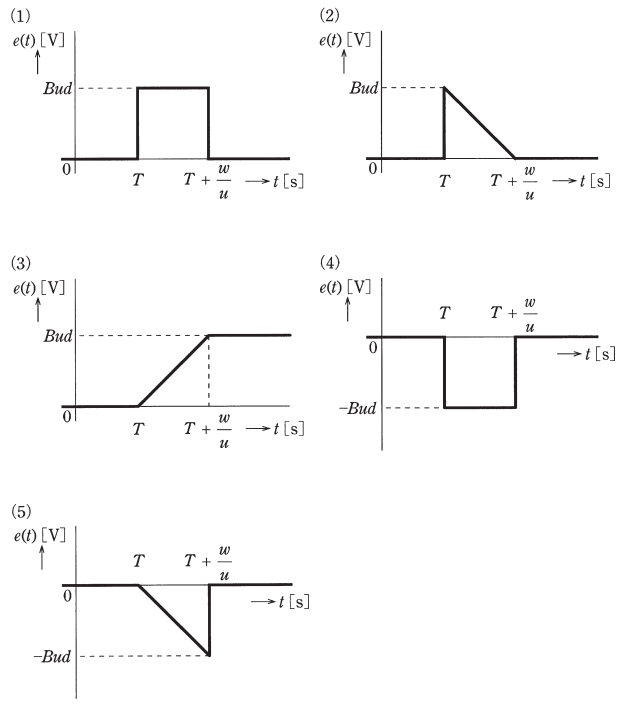
ファラデーの電磁誘導の法則で解答を導きます。
三角形のループ回路がソレノイドの内側(磁束のある領域)に入るまでは、磁束の時間的な変化がないので、誘導起電力は 0[V]です。
三角形のループ回路がソレノイドの内側に入ると誘導起電力が発生します。磁束の時間的な変化は、三角形のループ回路が移動すれば、徐々に大きくなり、抵抗がついている導線と平行な部分に到達する瞬間が最大になります。
三角形のループ回路が完全に磁束の中に入ってしまうと、磁束の時間的な変化がなくなってしまうので誘導起電力は 0[V]です。
したがって、$e(t)$ を示す図は、(5)が当てはまります。
答え (5)
電験三種の理論科目に出題される「電磁気分野」のページ
1.磁力線と磁束
2.アンペールの法則
3.フレミングの左手の法則
4.電流が磁界から受ける力
5.ヒステリシス曲線と損失
6.電磁誘導(レンツの法則とファラデーの法則)
7.自己インダクタンス
8.相互インダクタンス
9.磁気エネルギー






