第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「アンペールの法則」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「アンペールの法則」の過去問題も解説しています。
直線電流がつくる磁界
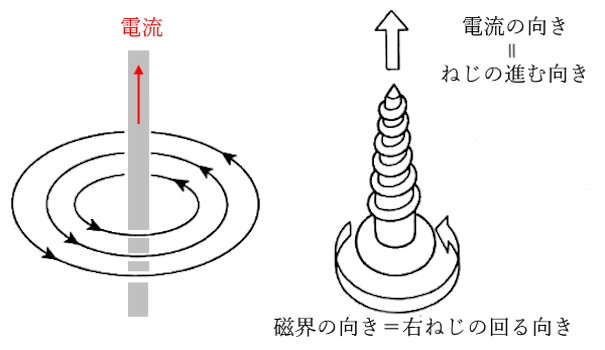
直線電流のまわりには磁界が発生します。導線を中心とした同心円状の磁界です。この磁界の向きは「ねじが進む方向」と一致します。電流が上向きに流れる場合、磁界の向きは反時計回りになります。この法則を「右ねじの法則」といいます。
右ねじの法則により、直線電流の周囲に発生した磁界の強さを求める公式は次のようになります。
直線電流がつくる磁界の強さ
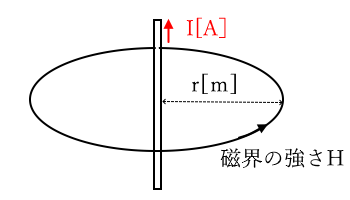
直線導体に電流 $I$ を流したとき、導体から $ r $ 離れた地点における磁界の強さ $H$ を求める公式
$H=\displaystyle\frac{I}{2πr}$[A/m]
$H$[A/m]:磁界の強さ
$I$[A]:直線導体に流れる電流
$r$[m]:直線導体からの距離
直線電流によって発生する磁界の強さは、電流が大きいほど、また距離が短いほど、強くなります。
磁界の強さの単位は、[N/Wb]または[A/m]ですが、電流がつくる磁界について考えるときは[A/m]を用います。
円形電流がつくる磁界
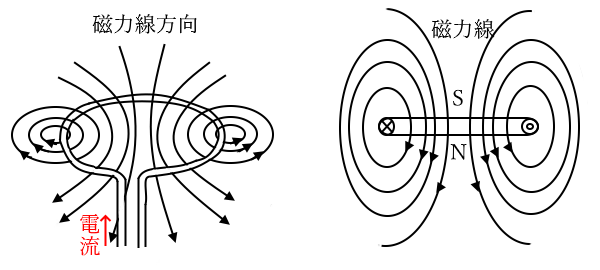
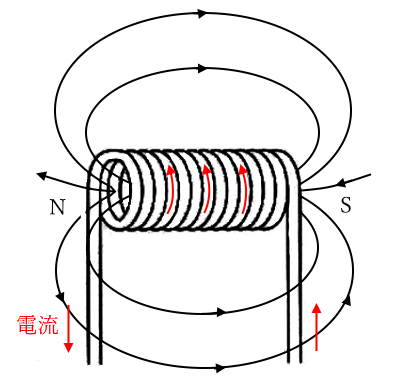
円形に巻いた導体を「コイル」といいます。導体に電流を流すと導体の周囲に磁束が発生し、磁界ができます。その法則はコイルにも当てはまります。コイルでは左側と右側で電流の向きが逆になりますので、「右ねじの法則」により、コイルの内部では同じ方向の磁界が発生します。
図中のⓞやⓍは電流の進む方向を表しています。ⓞは手前に向かっている様子を表し、Ⓧは奥へ行く様子を表しています。弓矢の矢をイメージするとわかりやすいと思います。ⓞが矢先で、Ⓧが矢尻です。
円形コイルにおける磁界の強さを求める公式は次のようになります。
円形電流がつくる磁界の強さ
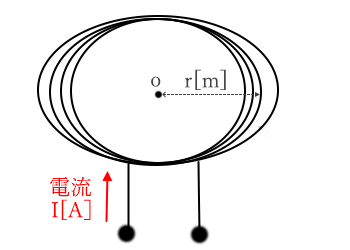
半径 $r$ の円形で、$I$ の大きさの電流がつくる磁界のうち、巻数 $N$ の円形コイルの中心 $o$ の磁界の強さ $H$ を求める公式
$H=\displaystyle\frac{NI}{2r}$[A/m]
$H$[A/m]:磁界の強さ
$N$[回]:コイルの巻数
$I$[A]:コイルに流れる電流
$r$[m]:コイルからの距離
ソレノイドコイルおける磁界
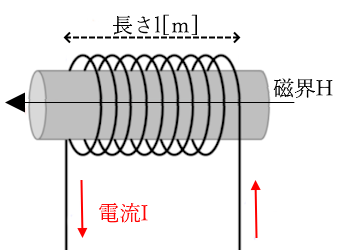
導線を密着させて、複数回巻いたコイルを「ソレノイド」といいます。ソレノイドは1巻きごとの磁界が加わり、内部の磁界が強くなります。
導線が密に巻かれていて、ソレノイドの長さが半径に比べて十分に長いとき、ソレノイドの内部の磁界は軸に平行で一様なものになります。また、外部の磁界はゼロとなります。このようなソレノイドを「理想的なソレノイド」といいます。
理想的なソレノイドの磁界の強さ
長さが $l$ で巻数 $N$ の理想的なソレノイドに、$I$ の電流が流れているときにつくる磁界の強さは $H$ を求める公式
$H=\displaystyle\frac{NI}{l}=nI$[A/m]
$H$[A/m]:磁界の強さ
$N$[回]:ソレノイドの巻数
$n$[回/m]:1m当たりの巻数
$I$[A]:ソレノイドに流れる電流
1m当たりの巻き数 $n =\displaystyle\frac{N}{l}$[回/m])
理想的なソレノイド内部に発生する磁界の強さ $H$ は、どの点においても等しくなります。
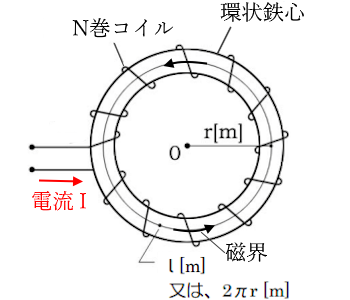
環状コイルにおける磁界の強さ
環状鉄心 にコイルを巻きつけたものを「環状コイル」といいます。環状コイルに電流を流すと、環状鉄心に磁束が発生して磁界ができます。その時の環状鉄心の中の磁界の強さを求める公式は、次のようになります。
環状鉄心の中の磁界の強さ
巻数 $N$ の環状コイルに電流 $I$ を流した時の、半径 $r$ の環状鉄心の中の磁界の強さ $H$ を求める公式
$H=\displaystyle\frac{NI}{l}=\displaystyle\frac{NI}{2πr}$[A/m]
$H$[A/m]:磁界の強さ
$N$[回]:環状コイルの巻数
$I$[A]:環状コイルに流れる電流
$r$[m]:環状鉄心の半径
$l$[m]:環状鉄心の長さ
電験三種-理論の過去問解説:アンペールの法則
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2000年(平成12年)問4【電験理論の過去問題】
真空中におかれた巻数 $N$ の円形コイルに直流電流 $I$[A]を流したとき、円形コイルの中心に発生する磁束の磁束密度[T]を表す式として、正しいのは次のうちどれか。ただし、円形コイルの半径を $a$[m]、真空の透磁率を $μ_{ 0 }$ [H/m]とする。
(1) $ \displaystyle \frac{ μ_{ 0 } NI}{ πa }$ (2) $ \displaystyle \frac{ NI}{ 2μ_{ 0 }a }$ (3) $ \displaystyle \frac{ μ_{ 0 }NI}{ a }$ (4) $ \displaystyle \frac{ NI}{ 2πμ_{ 0 }a }$ (5) $ \displaystyle \frac{ μ_{ 0 } NI}{ 2a }$
半径 $a$[m]の巻数 $N$ の円形コイルに電流 $I$[A]を流したときの中心の磁界の強さ $H$[A/m]は
$H=\displaystyle \frac{ NI}{ 2a }$[A/m]
磁束密度を $B$[T]、透磁率を $μ_0$[A/m]とすると、
$B=μ_{ 0 }H$[T]
$B=\displaystyle \frac{ μ_{ 0 }NI}{ 2a }$[T]
答え (5)
2003年(平成15年)問3【電験理論の過去問題】
図のように、A、B 2本の平行な直線導体があり、導体Aには 1.2[A]の、導体Bにはそれと反対方向に 3[A]の電流が流れている。導体AとBの間隔が $l$[m]のとき、導体Aより 0.3[m]離れた点Pにおける合成磁界が零になった。 $l$[m]の値として、正しいのは次のうちどれか。
ただし、導体A、Bは無限長とし、点Pは導体A、Bを含む平面上にあるものとする。
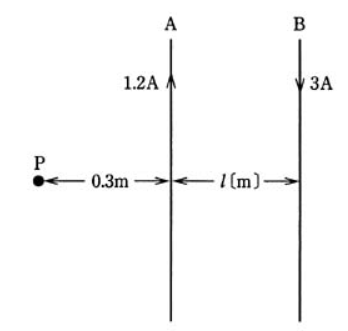
(1) 0.24 (2) 0.45 (3) 0.54 (4) 0.75 (5) 1.05
$I $[A]の直線電流から $ r $[m]離れた地点の磁場の強さ $H$[A/m]は、
$H=\displaystyle\frac{I}{2πr}$[A/m]
点Pにおける、Aの導体が作る磁界を $H_A$[A/m]、Bの導体が作る磁界を $H_B$[A/m]とすると、
$H_A=\displaystyle\frac{I}{2πr}=\displaystyle\frac{0.2}{2π×0.3}$[A/m]
$H_B=\displaystyle\frac{I}{2πr}=\displaystyle\frac{3}{2π×(l+0.3)}$[A/m]
題意より
$H_A=H_B$
$\displaystyle\frac{I}{2πr}=\displaystyle\frac{0.2}{2π×0.3}=\displaystyle\frac{I}{2πr}=\displaystyle\frac{3}{2π×(l+0.3)}$
$l=0.45$[m]
答え (2)
2005年(平成17年)問3【電験理論の過去問題】
無限に長い直線状導体に直流電流を流すと、導体の周りに磁界が生じる。この磁界中に小磁針を置くと、小磁針の( ア )は磁界の向きを指して静止する。そこで、小磁針を磁界の向きに沿って少しずつ動かしていくと、導体を中心とした( イ )の線が得られる。この線に沿って磁界の向きに矢印をつけたものを( ウ )という。
また、磁界の強さを調べてみると、電流の大きさに比例し、導体からの( エ )に反比例している。
上記の記述中の空白箇所(ア), (イ), (ウ)及び (エ)に記入する語句として、正しいものを組み合わせたのは次のうちどれか。

磁石の磁力線はN極から出てS極に入ります。磁力線に小磁針を近づけると、小磁針のS極が磁石のN極方向を指すことになります。したがって、磁石の磁力線の発生する方向を小磁針のS極が指し、磁力線の到達方向を小磁針のN極が指すことになります。
$I $[A]の直線電流から $ r $[m]離れた地点の磁場の強さ $H$[A/m]は、次式で表されます。
$H=\displaystyle\frac{I}{2πr}$[A/m]
無限に長い直線状導体に直流電流を流すと、導体の周りに磁界が生じる。この磁界中に小磁針を置くと、小磁針の( N極 )は磁界の向きを指して静止する。そこで、小磁針を磁界の向きに沿って少しずつ動かしていくと、導体を中心とした( 同心円状 )の線が得られる。この線に沿って磁界の向きに矢印をつけたものを( 磁力線 )という。
また、磁界の強さを調べてみると、電流の大きさに比例し、導体からの( 距離 )に反比例している。
答え (4)
2007年(平成19年)問1【電験理論の過去問題】
図1のように、無限に長い直線状導体Aに直流電流 $I_{ 1}$[A]が流れているとき、この導体から $a$[m]離れた点Pでの磁界の大きさは $H_{ 1}$[A/m]であった。一方、図2のように半径 $a$[m]の一巻きの円形コイルBに直流電流 $I_{ 2}$[A]が流れているとき、この円の中心点Oでの磁界の大きさは $H_{ 2}$[A/m]であった。$H_{ 1}=H_{ 2}$であるときの $I_{ 1}$と $I_{ 2}$の関係を表す式として、正しいのは次のうちどれか。
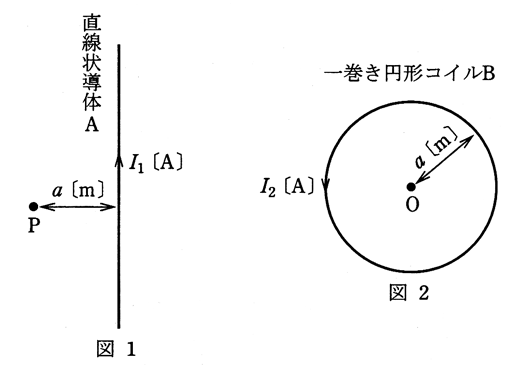
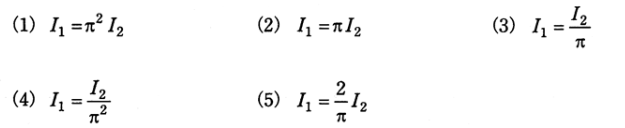
直線状導体Aによって発生する磁界の強さ$H_{ 1}$[A/m]は、
$H_{ 1}=\displaystyle\frac{I_{ 1}}{2πa}$[A/m]
一巻きの円形コイルBによって発生する磁界の強さ$H_{ 2}$[A/m]は、
$H_{ 2}=\displaystyle\frac{I_{ 2}}{2a}$[A/m]
題意より、$H_{ 1}=H_{ 2}$なので、
$\displaystyle\frac{I_{ 1}}{2πa}=\displaystyle\frac{I_{ 2}}{2a}$
$I_{ 1}=πI_{ 2}$
答え (2)
2009年(平成21年)問4【電験理論の過去問題】
図のように、点Oを中心とするそれぞれ半径 1[m]と半径 2[m]の円形導線の $\displaystyle\frac{1}{4}$ と、それらを連結する直線状の導線からなる扇形導線がある。この導線に図に示す向きに直流電流 $I=8$[A]を流した場合、点Oにおける磁界[A/m]の大きさとして、正しいのは次のうちどれか。
ただし、扇形導線は同一平面上にあり、その巻数は一巻きである。
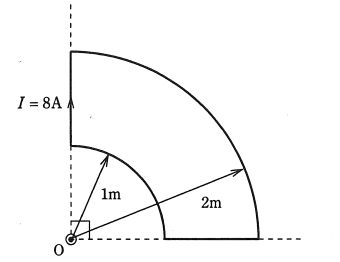
(1) 0.25 (2) 0.5 (3) 0.75 (4) 1.0 (5) 2.0
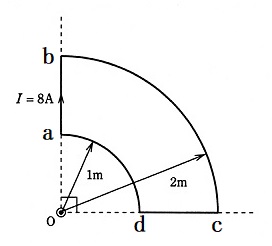
電流 $I$ の a から b と c から d の区間の磁界は、点Oに関係しません。一巻きの円形コイルによって発生する磁界の強さ $H$ は
$H=\displaystyle\frac{I}{2r}$[A/m]
扇形導線は円形の $\displaystyle\frac{1}{4}$ になっていますので、
$H_{ da}=\displaystyle\frac{1}{4}×\displaystyle\frac{8}{2×1}=1$[A/m]
$H_{ bc}=\displaystyle\frac{1}{4}×\displaystyle\frac{8}{2×2}=0.5$[A/m]
点Oにおける磁界の大きさ $H$[A/m]は向きを考慮すると、
$H=H_{ da}-H_{ bc}=0.5$[A/m]
答え (2)
2011年(平成23年)問4【電験理論の過去問題】
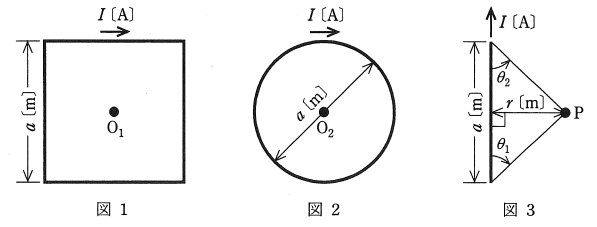
図1のように、1辺の長さが $a$[m]の正方形のコイル(巻数:1)に直流電流 $I$[A]が流れているときの中心点 $O_1$ の磁界の大きさを $H_1$[A/m]とする。また、図2のように、直径 $a$[m]の円形コイル(巻数:1)に直流電流 $I$[A]が流れているときの中心点 $O_2$ の磁界の大きさを $H_2$[A/m]とする。このとき、磁界の大きさの比 $\displaystyle\frac{H_1}{H_2}$ の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,中心点 $O_1$,$O_2$ はそれぞれ正方形のコイル,円形のコイルと同一平面上にあるものとする。
参考までに、図3のように,長さ a[m]の直線導体に直流電流 $I$[A]が流れているとき、導体から距離 $r$[m]離れた点Pにおける磁界の大きさ $H$[A/m]は、 $H=\displaystyle\frac{I}{4πr}(cosθ_1+cosθ_2)$ で求められる(角度 $θ_1$ と $θ_2$の定義は図参照)。
(1) 0.45 (2) 0.90 (3) 1.00 (4) 1.11 (5) 2.22
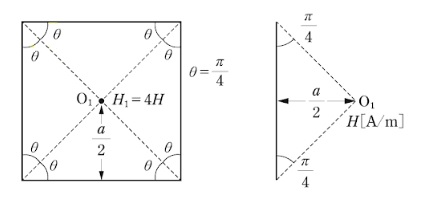
正方形のコイルについて、中心点 $O_1$ の磁界の大きさを $H_1$[A/m]は、コイル一辺が作る磁界の 4 倍になります。図3の $r,θ_1,θ_2$ は、$r=\displaystyle\frac{a}{2}$,$θ_1=\displaystyle\frac{π}{4}$,$θ_2=\displaystyle\frac{π}{4}$ となります。
正方形のコイル(巻数:1)に直流電流 $I$[A]が流れているときの中心点 $O_1$ の磁界の大きさを $H_1$[A/m]は、
$\begin{eqnarray}H_1&=&\displaystyle\frac{I}{4πr}(cosθ_1+cosθ_2)×4\\\\&=&\displaystyle\frac{I}{4π×\displaystyle\frac{a}{2}}(cos\displaystyle\frac{π}{4}+cos\displaystyle\frac{π}{4})×4\\\\&=&\displaystyle\frac{2\sqrt{ 2 }I}{πa}[A/m]\end{eqnarray}$
直径 $a$[m]の円形コイル(巻数:1)に直流電流 $I$[A]が流れているときの中心点 $O_2$ の磁界の大きさを $H_2$[A/m]は、
$H_2=\displaystyle\frac{I}{2×\displaystyle\frac{a}{2}}=\displaystyle\frac{I}{a}$[A/m]
よって、磁界の大きさの比 $\displaystyle\frac{H_1}{H_2}$ は、
$\displaystyle\frac{H_1}{H_2}=\displaystyle\frac{\displaystyle\frac{2\sqrt{ 2 }I}{πa}}{\displaystyle\frac{I}{a}}=\displaystyle\frac{2\sqrt{ 2 }}{π}=0.90$
答え (2)
2014年(平成26年)問4【電験理論の過去問題】
図のように、十分に長い直線状導体A,Bがあり、AとBはそれぞれ直角座標系の $x$ 軸と $y$ 軸に沿って置かれている。Aには $+x$ 方向の電流 $Ix$[A]が、Bには $+y$ 方向の電流 $Iy$[A]が、それぞれ流れている。$Ix >0$,$Iy >0$ とする。
このとき、$xy$ 平面上で $Ix$ と $Iy$ のつくる磁界が零となる点($x$[m],$y $[m])の満たす条件として、正しいものを次の(1)~(5)のうちから一つ選べ。ただし、$x≠0$、$y≠0$ とする。
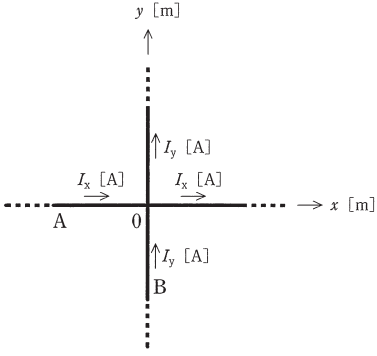
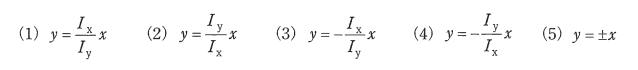
直線状導体A,Bが作る磁界の向きは図のようになります。
点(x,y)における、直線状導体A,Bが作る磁界の大きさをそれぞれ、$H_A$,$H_B$とすると、
$H_A=\displaystyle\frac{Ix}{2πy}$
$H_B=\displaystyle\frac{Iy}{2πx}$
x>0,y>0 の領域では、磁界の向きは反対向きなので、$H_A=H_B$ のとき、磁界は零になります。
$\displaystyle\frac{Ix}{2πy}=\displaystyle\frac{Iy}{2πx}$
$y=\displaystyle\frac{Ix}{Iy}x$
x<0,y>0 の領域では、磁界の向きは同じ向きなので、磁界が零になる点はありません。
x<0,y<0 の領域では、磁界の向きは反対向きなので、$H_A=H_B$ のとき、磁界は零になります。
$\displaystyle\frac{Ix}{2πy}=\displaystyle\frac{Iy}{2πx}$
$y=\displaystyle\frac{Ix}{Iy}x$
x>0,y<0 の領域では、磁界の向きは同じ向きなので、磁界が零になる点はありません。
答え (1)
2016年(平成28年)問3【電験理論の過去問題】
図のように、長い線状導体の一部が点Pを中心とする半径 $r $[m]の半円形になっている。この導体に電流 $I$[A]を流すとき、点Pに生じる磁界の大きさ $H$[A/m]はビオ・サバールの法則より求めることができる。$H$ を表す式として正しいものを、次の(1)~(5)のうちから一つ選べ。
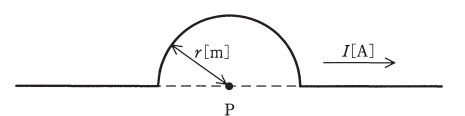
半径 $r $[m]の円の形で、$I $[A]の大きさの電流がつくる磁界のうち、円の中央部分の磁界の強さ $H$[A/m]は、
$H=\displaystyle\frac{I}{2r}$[A/m]
本問は、半円なので磁界の強さ $H$ は半分になります。
$H=\displaystyle\frac{I}{2r}×\displaystyle\frac{1}{2}=\displaystyle\frac{I}{4r}$[A/m]
答え (2)
2017年(平成29年)問17【電験理論の過去問題】
巻数 $N$ のコイルを巻いた鉄心1と、空隙(エアギャップ)を隔てて置かれた鉄心2からなる図1のような磁気回路がある。この二つの鉄心の比透磁率はそれぞれ $μ_{r1}=2000$,$μ_{r2}=1000$ であり、それらの磁路の平均の長さはそれぞれ $I_1=200mm$,$I_2=98mm$、空隙長は $δ=1mm$ である。ただし、鉄心1及び鉄心2のいずれの断面も同じ形状とし、磁束は断面内で一様で、漏れ磁束や空隙における磁束の広がりはないものとする。このとき、次の(a)及び(b)の問に答えよ。
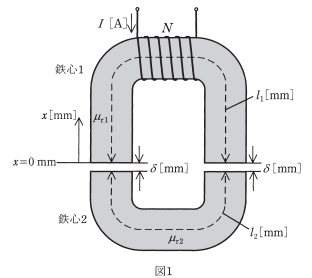
(a) 空隙における磁界の強さ $H_0$ に対する磁路に沿った磁界の強さ $H$ の比 $\displaystyle\frac {H}{H_0}$ を表すおおよその図として、最も近いものを図2の(1)~(5)のうちから一つ選べ。
ただし、図1に示す $x=0mm$ から時計回りに磁路を進む距離を $x$[mm]とする。また、図2は片対数グラフであり、空隙長 $δ$[mm]は実際より大きく表示している。
(b) コイルに電流 $I=1A$ を流すとき、空隙における磁界の強さ $H_0$ を $2×10^4A/m$ 以上とするのに必要なコイルの最小巻数 $N$ の値として、最も近いものを次の(1)〜(5)のうちから一つ選べ。
(1) 24 (2) 44 (3) 240 (4) 4400 (5) 40400
(a)鉄心1の磁界の強さを $H_1$[A/m],鉄心2の磁界の強さを $H_1$[A/m],空隙における磁界の強さ $H_0$[A/m]とすると、
$H_1=\displaystyle\frac{ϕ}{μ_0μ_{r1}A}=\displaystyle\frac{ϕ}{2000μ_0A}$[A/m]
$H_2=\displaystyle\frac{ϕ}{μ_0μ_{r2}A}=\displaystyle\frac{ϕ}{1000μ_0A}$[A/m]
$H_0=\displaystyle\frac{ϕ}{μ_0A}$[A/m]
$H_0$ に対する磁路に沿った磁界の強さ $H$ の比 $\displaystyle\frac {H}{H_0}$ は、
$0≦x≦200$のとき
$\displaystyle\frac {H_1}{H_0}=\displaystyle\frac {1}{2000}=5×10^{-4}$
$200<x≦201$のとき
$\displaystyle\frac {H_0}{H_0}=1$
$201<x≦299$のとき
$\displaystyle\frac {H_2}{H_0}=\displaystyle\frac {1}{1000}=1×10^{-3}$
$299<x≦300$のとき
$\displaystyle\frac {H_0}{H_0}=1$
答え(2)
(b)環状コイルにおける磁界の強さ $H$[A/m]は、$H=\displaystyle\frac{NI}{l}$ で表すことができます。ただし、磁界の強さが一定ではありませんので、「鉄心1」「鉄心2」「空隙」の3領域について磁界の強さと長さの積を求め、合計が電流の総量と等しくなると考えます。つまり、次の式が成り立ちます。
$H_1l_1+H_2l_2+2H_0δ=NI$
式を変形すると、
$N=\displaystyle\frac {\displaystyle\frac {H_1}{H_0}l_1+H_2l_2+2H_0δ}{I}=\displaystyle\frac{(\displaystyle\frac {H_1}{H_0}l_1+\displaystyle\frac {H_2}{H_0}l_2+2δ)H_0}{I}$
コイルに電流 $I=1A$ を流すとき、空隙における磁界の強さ $H_0$ を $2×10^4A/m$ 以上ですので、各数値を代入すると、
$\begin{eqnarray}N &=& \displaystyle\frac{(\displaystyle\frac {H_1}{H_0}l_1+\displaystyle\frac {H_2}{H_0}l_2+2δ)H_0}{I}\\\\ &=& \displaystyle\frac{(5×10^{-4}×200×10^{-3}+1×10^{-3}×98×10^{-3}+2×1×10^{-3})×2×10^{-3}}{1}\\\\ &=&43.96\end{eqnarray}$
答え(2)
電験三種の理論科目に出題される「電磁気分野」のページ
1.磁力線と磁束
2.アンペールの法則
3.フレミングの左手の法則
4.電流が磁界から受ける力
5.ヒステリシス曲線と損失
6.電磁誘導(レンツの法則とファラデーの法則)
7.自己インダクタンス
8.相互インダクタンス
9.磁気エネルギー






