このページでは、電流が磁界から受ける力について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題された電流が磁界から受ける力の過去問題も解説しています。
平行な直線導線に流れる電流間に働く力
平行な導線に電流が流れていると、それぞれの導線に流れる電流がつくる磁界によって、導線は力を受け、導線同士が引き合ったり反発し合ったりします。
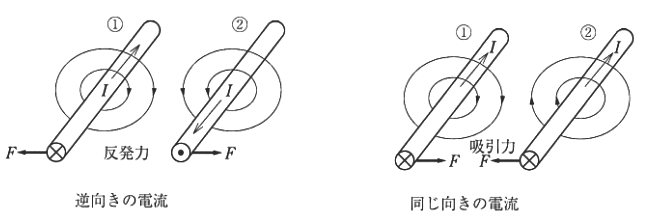
導線①と②を、距離 r[m]離して平行に置き、それぞれに電流 I1,I2[A]を流します。導線①に流れる電流 I1[A]がつくる r[m]離れた地点の磁界の強さ H1[A/m]は、次式で表されます。
$H_{ 1 }=\displaystyle\frac{I_{ 1 }}{2πr}$[A/m]
導線②のうち、長さ l の部分が、磁界から受ける力 F2[N]は、F=BIl=μ0HIl[N]より
$F_{ 2}=μ_{ 0 }H_{ 1}I_{ 2}l=\displaystyle\frac{μ_{ 0 }I_{ 1 }I_{ 2}}{2πr}l$[N]
となります。同じように導線①が受ける力 F1[N]について考えていくと、
$F_{ 1}=\displaystyle\frac{μ_{ 0 }I_{ 1 }I_{ 2}}{2πr}l$[N]
まったく同じになります。これは作用⋅反作用の法則です 。力の向きは、フレミングの左手の法則により、平行導線が互いに逆向きの電流なら反発力、同じ方向なら吸引力になります。
方形のコイルに働く力
長方形の一巻きコイルを一様な磁界中に置いたときに働く力について考えてみます。
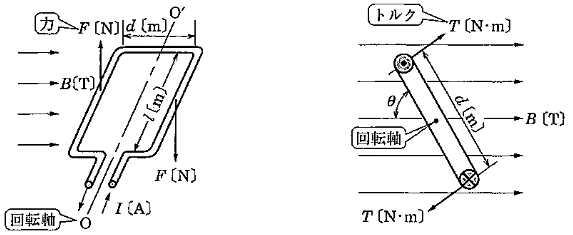
図のようなコイルに電流 I[A]を流すと、長さ l[m]の辺は、F=BIl=μ0HIl[N]の力を受けます。
力の方向はフレミング左手の法則より、それぞれの辺が上向きと下向きになります。このように、方向が反対向きの2つの力を偶力といい、偶力が働くと物体は回転をはじめます。物体に回転を生じさせるような力の性質を「モーメント」といいます。
また、固定された回転軸を中心に働く回転力を「トルク $T$(単位:ニュートン毎メートル[N/m])」といい次式で表されます。
$T=Fdcosθ=BIldcosθ$ [N/m]
電験三種-理論(電磁気)過去問題
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2002年(平成14)問4
図のように、空間に一様に分布する磁束密度 B=0.4[T]の磁界中に、辺の長さがそれぞれ a=15[cm]、b=6[cm]で、巻数 N=20 の長方形のコイルが置かれている。このコイルに直流電流 I=0.8[A]を流したとき、このコイルの回転軸 OO’ を軸としてコイルに生じるトルク T[Nm]の最大値として、最も近いのは次のうちどれか。
ただし、コイルの辺aは磁界と直交し、OO’ は辺bの中心を通るものとする。また、コイルの太さは無視し、流れる電流によって磁界は乱されないものとする。
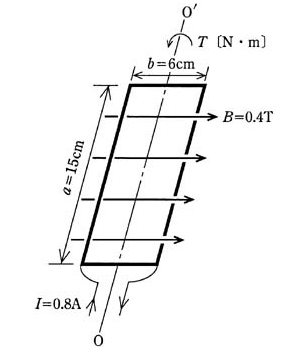
(1) 0.011 (2) 0.029 (3) 0.033 (4) 0.048 (5) 0.058
2002年(平成14)問4 過去問解説
コイルの辺aは、磁界と直交しているので、
F=BIa=0.4×0.8×0.15=0.048[N]
巻数 N=20 なので、T=NFbより
T=NFb=20×0.048×0.06=0.058[Nm]
答え (5)
2005年(平成17)問4
真空中において、同一平面内に、無限に長い 3本の導体A、Bが互いに平行に置かれている。導体Aと導体Bの間隔は 2[m]、導体Bと導体Cの間隔は 1[m]である。
導体には図に示す向きに、それぞれ 2[A],3[A],3[A]の直流電流が流れているものとする。このとき、導体Bが、導体Aに流れる電流と導体Cに流れる電流によって受ける 1[m]当たりの力の大きさ F[N/m]の値として、正しいのは次のうちどれか。
ただし、真空の透磁率を $μ_{0}=4π×10^{ -7}$[H/m]とする。
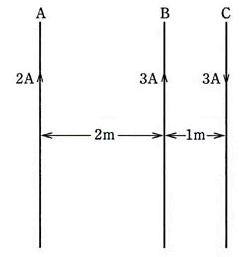
(1) 1.05×10-6 (2) 1.20×10-6 (3) 1.50×10-6 (4) 2.10×10-6 (5) 2.40×10-6
2005年(平成17)問4 過去問解説
導体Bが導体Aから受ける力を FAB [N/m] 、導体Bが導体Cから受ける力を FCB [N/m] とすると、
$F_{ AB}=\displaystyle\frac{4π×10^{ -7}×2×3}{2π×2}×1=6×10^{ -7}$
$F_{ CB}=\displaystyle\frac{4π×10^{ -7}×3×3}{2π×1}×1=18×10^{ -7}$
FAB は吸引力、FCB は反発力となるので、そのベクトル和 F [N/m] は
$F=F_{ AB}+F_{ CB}=2.4×10^{ -6}$[N/m]
答え (5)
2010年(平成22)問4
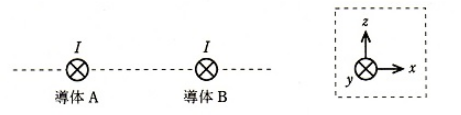
図に示すように、直線導体 A及び Bがy方向に平行に配置され、両導体に同じ大きさの電流 I が共に+y方向に流れているとする。このとき、各導体に加わる力の方向について、正しいものを組み合わせたのは次のうちどれか。
なお、xyz座標の定義は、破線の枠内の図で示した通りとする。

2010年(平成22)問4 過去問解説
平行導線が互いに逆向きの電流なら反発力、同じ方向なら吸引力になります。題意より電流は同じ方向に流れるので吸引力となります。
答え (2)
2012年(平成24)問4
真空中に、2本の無限長直線状導体が 20[cm]の間隔で平行に置かれている。一方の導体に 10[A]の直流電流を流しているとき、その導体には 1[m]当たり 1×10-6 の力が働いた。他方の導体に流れている直流電流 I[A]の大きさとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、真空の透磁率は μ0=4π×10-7 [H/m]である。
(1) 0.1 (2) 1 (3) 2 (4) 5 (5) 10
2012年(平成24)問4 過去問解説
一方の導線が受ける力 F1 について考えていくと、
$F_{ 1}=\displaystyle\frac{μ_{ 0 }I_{ 1 }I_{ 2}}{2πr}l$
$1×10^{-6}=\displaystyle\frac{4π×10^{ -7}×10×I_{ 2}}{2π×0.2}×1$
$I_{ 2}=0.1$
答え (1)
2013年(平成25)問3
磁界及び磁束に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- 1[m]当たりの巻数が N の無限に長いソレノイドに電流 I[A]を流すと、ソレノイドの内部には磁界 H=NI[A/m]が生じる。磁界の大きさは、ソレノイドの寸法や内部に存在する物質の種類に影響されない。
- 均一磁界中において、磁界の方向と直角に置かれた直線上導体に直流電流を流すと、導体には電流の大きさに比例した力が働く。
- 2本の平行な直線状導体に反対向きの電流を流すと、導体には導体間距離の2乗に反比例した反発力が働く。
- フレミングの左手の法則では、親指の向きが導体に働く力の向きを示す。
- 磁気回路において、透磁率は電気回路の導電率に、磁束は電気回路の電流にそれぞれ対応する。
2013年(平成25)問3 過去問解説
(1),(2),(4),(5)は正しい記述です。
2本の平行な直線状導体に反対向きの電流を流すと
$F=\displaystyle\frac{μ_{ 0 }I_{ 1 }I}{2πr}l$[N]
の力が発生します。
したがって(3)の記述は、「2本の平行な直線状導体に反対向きの電流を流すと、導体には導体間距離の2乗に反比例した反発力が働く。」になります。
答え (3)
2013年(平成25)問4
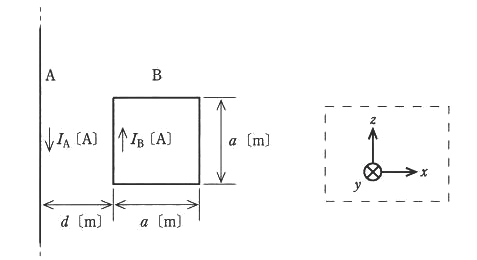
図のように、透磁率 $μ_0$[H/m]の真空中に無限に長い直線状導体 A と 1 辺 $a$[m]の正方形のループ状導体 B が距離 $d $[m]を隔てて置かれている。A と B は $xy$ 平面上にあり、 A は $z$ 軸と平行、 B の各辺は $x$ 軸又は $z$ 軸と平行である。A、 B には直流電流 $I_A$[A],$I_B$[A]が、それぞれ図示する方向に流れている。このとき、B に加わる電磁力として、正しいものを次の(1)~(5)のうちから一つ選べ。
なお、$xyz$ 座標の定義は、破線の枠内の図で示したとおりとする。

2013年(平成25)問4 過去問解説
磁界中にある導体に働く力 $F$[N]は、
$F=BIlsinθ$
導体が磁界と垂直のときは、$sinθ=1$、導体が磁界と平行のときは、$sinθ=0$ となります。正方形のループ状導体の上下の辺には、力が発生しません。
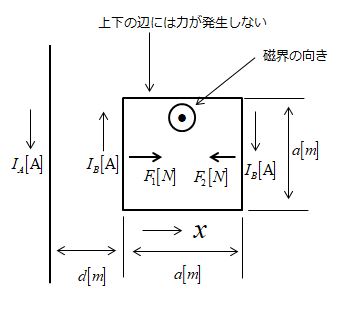
図の $F_1$[N]および $F_2$[N]は次のようになります。
$F_1=\displaystyle\frac{μ_{ 0 }I_{ A }I_{ B}}{2πd}a$
$F_2=\displaystyle\frac{μ_{ 0 }I_{ A }I_{ B}}{2π(d+a)}a$
導体 B に加わる電磁力を F [N] は、$F=F1−F2$ ですので、
$F=\displaystyle\frac{μ_{ 0 }I_{ A }I_{ B}}{2πd}a−\displaystyle\frac{μ_{ 0 }I_{ A }I_{ B}}{2π(d+a)}a=\displaystyle\frac{μ_{ 0 }I_{ A }I_{ B}}{2πd(d+a)}a^2$
答え (2)





