第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「導体球と同心球導体の静電容量」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「導体球と同心球導体の静電容量」の過去問題も解説しています。
導体球表面の電界の強さ
導体球とは球状の導体のことで、その内部には電界が存在しません。導体は電気を通す物質です。つまり、自由に動き回る電子が存在し、導体球が帯電すると電荷は表面に分布します。
真空中に $Q$[C]の電荷をもつ半径 $r$[m]導体球表面の電界の強さ $E$[V/m]は次の式で求めることができます。
導体球表面の電界の強さ $E$ を求める公式
$E=\displaystyle \frac{ 1 }{ 4πε_{ 0 } }\frac{ Q }{ r^2}$
$E$:電界の強さ[V/m]
$ε_0$:真空の誘電率
$Q$:電荷[C]
$r$:球の半径[m]
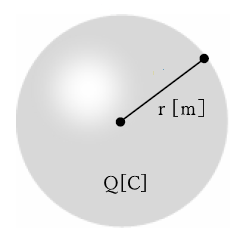
点電荷が作る電界の強さ $E$ を求める公式と同じ式になります。尚、導体球表面に電界は発生しますが、導体球内部の電界の強さは 0 になります。
導体球表面の電位と静電容量
真空中に $Q$[C]の電荷をもつ半径 $r$[m]導体球表面の電位 $V$[V]は次の式で求めることができます。
導体球表面の電位 $V$ を求める公式
$ V=\displaystyle \frac{ Q }{ 4πε_{ 0 } r }$[V]
$V$[V]:電位
$ε_0$:真空の誘電率
$Q$[C]:電荷
$r $[m]:球の半径

点電荷が作る電位 $V$ を求める公式と同じ式になります。
また、導体球の静電容量 $C$[F]は、次式で表されます。
導体球の静電容量 $C$ を求める公式
$C=\displaystyle\frac{Q}{V}=4πε_{ 0 }r$[F]
$C$[F]:導体球の静電容量
$ε_0$:真空の誘電率
$Q$[C]:電荷
$r $[m]:球の半径

同心球導体の静電容量
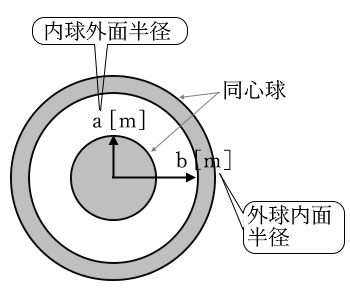
同心球導体とは、大小2つの球殻がある導体です。二つの球の中心は一致しています。それぞれの球の半径を $a,b$($a<b$)とします。
内球外面の電位を $V_a$[V]、外球内面の電位を $V_b$[V]とすると、電位差 $V_{ab}$[V]は、次式で表されます。
同心球導体の電位差 $V_{ab}$ を求める公式
$V_{ab}=V_a-V_b=\displaystyle\frac{Q}{4πε_0}(\displaystyle\frac{1}{a}-\displaystyle\frac{1}{b})$[V]
$V_{ab}$[V]:電位差
$ε_0$:真空の誘電率
$Q$[C]:電荷
$a,b$[m]:球の半径
また、同心球導体の静電容量 $C_{ab}$[F]は、次式で表されます。
同心球導体の静電容量 $C_{ab}$ を求める公式
$C_{ab}=\displaystyle\frac{Q}{V_{ab}}=\frac{Q}{\displaystyle\frac{Q}{4πε_0}(\displaystyle\frac{1}{a}-\displaystyle\frac{1}{b})}=\displaystyle\frac{4πε_0ab}{b-a}$[F]
$C_{ab}$[F]:同心球導体の静電容量
$ε_0$:真空の誘電率
$Q$[C]:電荷
$a,b$[m]:球の半径

電験三種-理論の過去問解説:導体球と同心球導体の静電容量
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1999年(平成11年)問5【電験理論の過去問題】
空気中に孤立した半径 a[m]の導体球に帯電できる最大の電荷[C]の値として、正しいものは次のうちどれか。ただし、空気の絶縁耐力及び誘電率はそれぞれ Em[V/m]及びε0[F/m]とする。
(1) $\displaystyle\frac{E_m}{4πε_oa^2}$ (2) $\displaystyle\frac{E_m}{4πε_oa}$ (3) $4πε_oaE_m$ (4) $4πε_oa^2E_m$ (5) $4πε_oa^3E_m$
電界の強さが空気の絶縁耐力に等しくなるとき、導体球に帯電できる電荷は最大となります。このときの電荷を Q[C]とすると、
$E_m=\displaystyle\frac{Q}{4πε_oa^2}$[V/m]
$Q=4πε_oa^2E_m$
答え (4)
2006年(平成18年)問1【電験理論の過去問題】
真空中に半径 6.37×106[m]の導体球がある。これの静電容量[F]の値として、最も近いのは次のうちどれか。
ただし、真空の誘電率をε0=8.85×10-12[F/m] とする。
(1) 7.08×10-4 (2) 4.45×10-3 (3) 4.51×103 (4) 5.67×104 (5) 1.78×105
球形の導体に電荷 Q[C]を与えたとき、半径 r[m]の導体球表面に生じる電位 V[V]は、
$V=\displaystyle\frac{Q}{4πε_or}$[V]
導体球の静電容量を C[F]とすると、
$C=\displaystyle\frac{Q}{V}=4πε_or$
$=4π×8.85×10^{-12}×6.37×10^6$
$=7.08×10^{-4}$[F]
答え (1)
2008年(平成20年)問17【電験理論の過去問題】
大きさが等しい二つの導体球A,Bがある。両導体球に電荷が蓄えられている場合、両導体球の間に働く力は、導体球に蓄えられている電荷の積に比例し、導体球間の距離の 2乗に反比例する。次の( a )及び( b )に答えよ。
(a) この場合の比例定数を求める目的で、導体球Aに +2×10-8[C]、導体球Bに +3×10-8 [C]の電荷を与えて、導体球の中心間距離で 0.3[m]隔てて両導体球を置いたところ、両導体球間に 6×10-5[N]の反発力が働いた。この結果から求められる比例定数[Nm2/C2]として、最も近いのは次のうちどれか。
ただし、導体球A,Bの初期電荷は零とする。また、両導体球の大きさは 0.3[m]に比べて極めて小さいものとする。
(1) 3×109 (2) 6×109 (3) 8×109 (4) 9×109 (5) 15×109
(b) 上記( a )の導体球 A,B を、電荷を保持したままで 0.3[m]の距離を隔てて固定した。ここで導体球A,Bと大きさが等しく電荷を持たない導体球Cを用意し、導体球Cをまず導体球Aに接触させ、次に導体球Bに接触させた。この導体球Cを導体球Aと導体球Bの間の直線上に置くとき、導体球Cが受ける力が釣り合う位置を導体球Aとの中心間距離[m]で表したとき、その距離に最も近いのは次のうちどれか。
(1) 0.095 (2) 0.105 (3) 0.115 (4) 0.124 (5) 0.135
(a) 導体球Aの電荷を QA[C]、導体球Bの電荷を QB[C]、両導体間の距離を r[m]、両導体間に働く力を FAB[N]、比例定数を k とすると、クーロンの法則より、
$F_{AB}=k・\displaystyle\frac{Q_A・Q_B}{r^2}$
$k=\displaystyle\frac{F_{AB}}{Q_A・Q_B}・r^2$
$=\displaystyle\frac{6×10^{-5}}{2×10^{-8} ×3×10^{-8} }×0.3^2=9×10^9$
答え (4)
(b) 電荷を持たない導体球Cと導体球Aを接触させると、導体球Aの電荷が導体球Cに移動して平衡します。その時の両導体球の電荷は、導体球Aの半分の電荷で平衡し、+1×10-8[C]になります。
次に導体球Cと導体球Bを接触させると、導体球Bの電荷と導体球Cの電荷の和の半分で平衡します。その時の両導体球の電荷は、導体球Aの半分の電荷で平衡し、(+3×10-8 +1×10-8)/2=+2×10-8[C]になります。
導体球Aと導体球Cの中心距離を $x$[m]とすると、クーロンの法則より、
$F_{AC}=k・\displaystyle\frac{Q_A・Q_C}{x^2}$
$F_{BC}=k・\displaystyle\frac{Q_B・Q_C}{(0.3-x)^2}$
導体球Cが受ける力が釣り合う位置は、$F_{AC}=F_{BC}$ となる位置です。
$k・\displaystyle\frac{Q_A・Q_C}{x^2}=k・\displaystyle\frac{Q_B・Q_C}{(0.3-x)^2}$
$\displaystyle\frac{Q_A}{x^2}=\displaystyle\frac{Q_B}{(0.3-x)^2}$
$\displaystyle\frac{1×10^{-8}}{x^2}=\displaystyle\frac{2×10^{-8}}{(0.3-x)^2}$
$(0.3-x)^2=2x^2$
$x=0.124$[m]
答え (4)
2013年(平成25年)問17【電験理論の過去問題】
空気中に半径 r[m]の金属球がある。次の(a)及び(b)の問に答えよ。
ただし、r= 0.01[m]、真空の誘電率をε0=8.854×10-12[F/m]、空気の比誘電率を 1.0 とする。
(a) この金属球が電荷 Q[C]を帯びたときの金属球表面における電界の強さ[V/m]を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1) $\displaystyle\frac{Q}{4πε_or^2}$ (2) $\displaystyle\frac{3Q}{4πε_or^3}$ (3) $\displaystyle\frac{Q}{4πε_or}$ (4) $\displaystyle\frac{Q^2}{8πε_or}$ (5) $\displaystyle\frac{Q^2}{2πε_or^2}$
(b) この金属球が帯びることのできる電荷 Q[C]の大きさには上限がある。空気の絶縁破壊の強さを 3×106[V/m]として、金属球表面における電界の強さが空気の絶縁破壊の強さと等しくなるような Q[C]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 2.1×10-10 (2) 2.7×10-9 (3) 3.3×10-8 (4) 2.7×10-7 (5) 3.3×10-6
(a) 金属球表面の電界の強さを E[V/m]とすると、
$E=\displaystyle\frac{Q}{4πε_or^2}$[V/m]
答え (1)
(b) (a)の解答より
$Q=4πε_or^2E$
$=4π×8.854×10^{-12}×0.01^2×3×10^6$
$=3.3×10^{-8}$[C]
答え (3)
電験三種の理論科目に出題される「静電気分野」のページ
1.クーロンの法則とは
2.電界とガウスの法則
3.静電界中の電位と電圧
4.静電誘導と誘電分極
5.平行平板コンデンサの静電容量
6.コンデンサの直列接続と並列接続
7.静電エネルギー
8.誘電体とコンデンサ
9.導体球と同心球導体の静電容量






