第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「静電エネルギーと並列接続」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「静電エネルギー」の過去問題も解説しています。
静電エネルギー
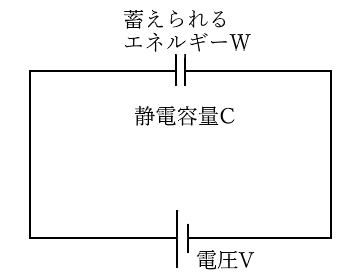
コンデンサーが電気量を蓄えるには仕事が必要です。コンデンサはその仕事 $W$(単位:ジュール[J])を静電エネルギーを電極間の電界に蓄えることができます。
コンデンサの端子に電圧 $V$[V]を印加したとき、電荷 $Q$[C]を蓄えたときの静電エネルギー $W$[J]は、次の公式で求めることができます。
コンデンサに蓄えられるエネルギー $W$ を求める公式
$W=\displaystyle\frac{1}{2}CV^2$[J]
$Q=CV$ より
$W=\displaystyle\frac{1}{2}CV^2=\displaystyle\frac{1}{2}QV=\displaystyle\frac{1}{2}\frac{Q^2}{C}$[J]
$W$[J]:コンデンサに蓄えられるエネルギー
$C$[F]:コンデンサの静電容量
$V$[V]:コンデンサにかかる電圧
電験三種-理論の過去問解説:静電エネルギー
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1998年(平成10年)問6【電験理論の過去問題】
電圧 $V$[V]に充電された静電容量 $C$[F]のコンデンサと全く充電されていない静電容量 $\displaystyle\frac{1}{2}C$[F]のコンデンサとがある。これら二つのコンデンサを並列に接続したとき、これらのコンデンサに蓄えられる全静電エネルギー[J]の値として、正しいものは次のうちどれか。
(1) $\displaystyle\frac{1}{9}CV^2$ (2) $\displaystyle\frac{1}{6}CV^2$ (3) $\displaystyle\frac{2}{9}CV^2$ (4) $\displaystyle\frac{1}{3}CV^2$ (5) $\displaystyle\frac{3}{8}CV^2$
コンデンサの静電容量を、それぞれ $C_{ 1 }$、$C_{ 2 }$とし、$C_{ 1 }$が $V$[V]に充電されているとします。コンデンサを並列接続した後の、合成静電容量を $C’$、充電電圧を $V’$[V]とすると、並列接続前後では、電荷量 $Q$ は変化しませんので、
$Q=C_{ 1 }V=C’V’=(C_{ 1 }+C_{ 2 })V’$
$V’=\displaystyle\frac{C_{ 1 }}{C_{ 1 }+C_{ 2 }}V$・・・①
全静電エネルギー $W$は
$W=\displaystyle\frac{1}{2}C’V’^2=\displaystyle\frac{1}{2}(C_{ 1 }+C_{ 2 })V’^2$・・・②
題意より $C_{ 1 }=C$、$C_{ 2 }=\displaystyle\frac{1}{2}C$ および ①式を ②式に代入すると
$\begin{eqnarray}W&=&\displaystyle\frac{(C_{ 1 }+C_{ 2 })}{2}×\biggl(\frac{C_{ 1 }V}{C_{ 1 }+C_{ 2 }}\biggl)^2\\&=&\displaystyle\frac{ 1 }{ 3 }CV^2\end{eqnarray}$
答え (4)
2000年(平成12年)問3【電験理論の過去問題】
静電容量 2[mF]のコンデンサを充電し、その電荷をある抵抗を通してすべて放電させたところ、抵抗で消費されたエネルギーは 10[J]であった。放電を開始する直前、コンデンサに蓄えられていた電荷[mC]の値として正しいのは次のうちどれか。
(1) 100 (2) 124 (3) 141 (4) 173 (5) 200
コンデンサーの端子に電圧 $V$[V]を印加したとき、電荷 $Q$[C]を蓄えたときの静電エネルギー $W$[J]は
$W=\displaystyle\frac{1}{2}CV^2=\displaystyle\frac{1}{2}QV=\displaystyle\frac{1}{2}\frac{Q^2}{C}$[J]
上式を変形すると
$\begin{eqnarray}Q&=&\sqrt{ 2 CW}\\\\&=&\sqrt{ 2×2×10^{-3}×10}\\\\&=&200[mC]\end{eqnarray}$
答え (5)
2006年(平成18年)問17【電験理論の過去問題】
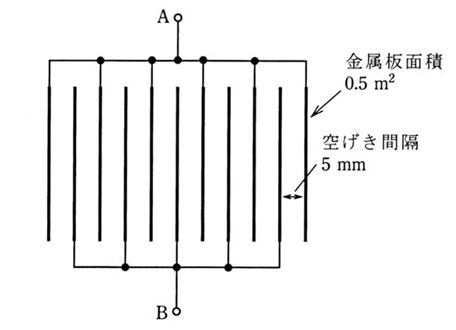
互いに 5[mm]の空げき間隔をおいて、平行平板状に並べられた11枚の同一形状の金属板がある。1枚の金属板の面積は 0.5[m2]とする。いま、図のようにこの金属板をそれぞれ1枚おきに接続して空気コンデンサをつくる。次の(a)及び(b)に答えよ。
ただし、真空の誘電率を $ε_0=8.85×10^{-12}$[F/m]とし、空気の比誘電率は、1.0とする。また、コンデンサの端効果は無視できるものとする。
(a) コンデンサの静電容量 $C$[pF]の値として、正しいのは次のうちどれか。
(1) 88.5 (2) 4430 (3) 8850 (4) 17.7×103 (5) 177×104
(b) コンデンサ極板間の電界強度を1000[kV/m]とするとき、コンデンサに蓄えられるエネルギー $W$[J]の値として、最も近いのは次のうちどれか。
(1) 1.11×10-3 (2) 5.54×10-2 (3) 1.11×10-1 (4) 2.21×10-1 (5) 2.21×10
(a) 問の空気コンデンサは、次の図のように置きかえることができます。
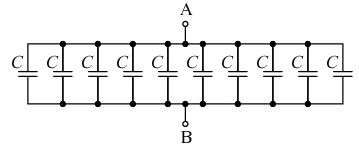
平行板コンデンサの合成静電容量 $C $[F]は、
$\begin{eqnarray}C&=&10×ε_0ε_s\displaystyle\frac{S}{d}\\\\&=&10×8.85×10^{-12}×1.0×\displaystyle\frac{0.5}{5×10^{-3}}\\\\&=&8.85×10^{-9}=8850×10^{-12}\end{eqnarray}$
答え (3)
(b) $V=Ed$ 、$W=\displaystyle\frac{1}{2}CV^2$ より
$V=Ed=1000×10^3×5×10^{-3}=5000$[V]
$W=\displaystyle\frac{1}{2}×8.85×10^{-9}×(5000)^2=1.11×10^{-1}$[J]
答え (3)
2007年(平成19年)問4【電験理論の過去問題】
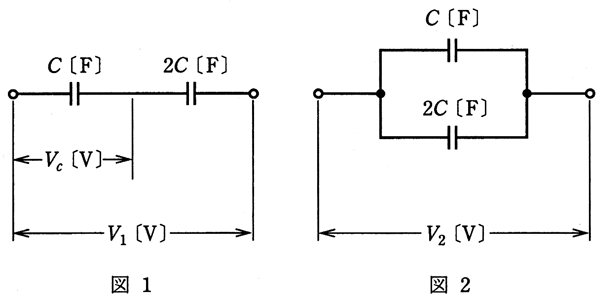
静電容量が $C$[F]と $2C$[F]の二つのコンデンサを図1、図2のように直列、並列に接続し、それぞれ $V_{ 1 }$[V]、$V_{ 2 }$[V]の直流電圧を加えたところ、両図の回路に蓄えられている総静電エネルギーが等しくなった。この場合、図1の $C$[F]のコンデンサの端子間の電圧を $V_{ C }$[V]としたとき、電圧比 $\displaystyle\left|\frac{V_{ C }}{V_{ 2 }}\right|$ の値として、正しいのは次のうちどれか。
(1) $\displaystyle\frac{\sqrt{ 2}}{9}$ (2) $\displaystyle\frac{2\sqrt{ 2}}{9}$ (3) $\displaystyle\frac{1}{\sqrt{ 2}}$ (4) $\sqrt{ 2}$ (5) 3.0
図1のように直列接続の場合、コンデンサに蓄えられる電荷 $Q$[C]は等しいので、
$Q=CV_{ C }=2C(V_{ 1 }-V_{ C })$
$\displaystyle\frac{1}{2}V_{ C }=(V_{ 1 }-V_{ C })$
図1の静電エネルギー $W_{ 1 }$は
$\begin{eqnarray}W_{ 1 }&=&\displaystyle\frac{1}{2}CV_{ C }^2+\frac{1}{2}×2C×(V_{ 1 }-V_{ C })^2\\&=&\displaystyle\frac{1}{2}CV_{ C }^2+\displaystyle\frac{1}{4}CV_{ C }^2\\&=&\displaystyle\frac{3}{4}CV_{ C }^2\end{eqnarray}$
図2の静電エネルギー $W_{ 2 }$は
$\begin{eqnarray}W_{ 2 }&=&\displaystyle\frac{1}{2}CV_{ 2 }^2+\frac{1}{2}×2CV_{ 2 }^2\\&=&\displaystyle\frac{6}{4}CV_{ 2 }^2\end{eqnarray}$
$W_{ 1 }=W_{ 2 }$なので
$\displaystyle\frac{3}{4}CV_{ C }^2=\displaystyle\frac{6}{4}CV_{ 2 }^2$
よって
$\displaystyle\left|\frac{V_{ C }}{V_{ 2 }}\right|=\sqrt{ 2}$
答え (4)
2007年(平成19年)問7【電験理論の過去問題】
図に示すRLC回路において、静電容量 C[F]のコンデンサが電圧 V[V]に充電されている。この状態でスイッチSを閉じて、それから時間が十分に経過してコンデンサの端子電圧が最終的に零となった。この間に抵抗 R[Ω]で消費された電気エネルギー[J]を表す式として、正しいのは次のうちどれか。
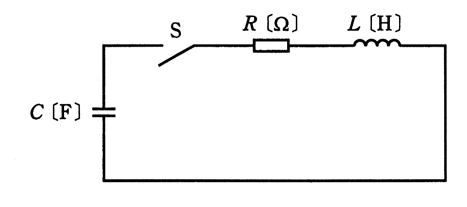
(1) $ \displaystyle\frac {1}{2}C^2V$ (2) $\displaystyle\frac {1}{2}CV^2$ (3) $ \displaystyle\frac {1}{2} \displaystyle\frac { V^2 }{ R } $ (4) $ \displaystyle\frac {1}{2} L^2V$ (5) $ \displaystyle\frac {1}{2} LV^2$
最終的にコンデンサの端子電圧が零になるので、求める電力=最初に $C$ にたまっていた静電エネルギーです。
$W=\displaystyle\frac{1}{2}CV^2$[J]
答え (2)
2008年(平成20年)問2【電験理論の過去問題】
次の文章は、平行板コンデンサに蓄えられるエネルギーについて述べたものである。
極板間に誘電率 $ε$[F/m]の誘電体をはさんだ平行板コンデンサがある。このコンデンサに電圧を加えたとき、蓄えられるエネルギー $W$[J]を誘電率 $ε$[F/m]、電極間の誘電体の体積 $V$[m3]、極板間の電界の大きさ $E$[V/m]で表現すると、$W$[J]は、誘電率 $ε$[F/m]の( ア ) に比例し、体積 $V$[m3]に( イ )し、電界の大きさ $E$[V/m]の( ウ )に比例する。
ただし、極板の端効果は無視する。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句として、正しいものを組み合わせたのは次のうちどれか。
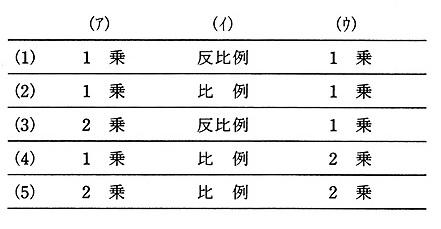
誘電率 $ε$[F/m]、極板間距離 $d$[m]、極板面積 $S$[m2]のコンデンサ容量 $C$[F]は、
$C=\displaystyle\frac{εS}{d}$
コンデンサの体積 V[m3]は、
$V=Sd$
電圧 $v$[V]は、電界の大きさを $E$[V/m]とすると、
$v=Ed$[V]
静電エネルギー $W$[J]は
$W=\displaystyle\frac{1}{2}Cv^2=\displaystyle\frac{1}{2}\displaystyle\frac{εS}{d}(Ed)^2$
$=\displaystyle\frac{1}{2}εE^2Sd=\displaystyle\frac{1}{2}εE^2V$[J]
したがって、$W$[J]は、誘電率 $ε$[F/m]の( 1乗 ) に比例し、体積 $V$[m3]に( 比例 )し、電界の大きさ $E$[V/m]の( 2乗 )に比例する。
答え (4)
2009年(平成21年)問5【電験理論の過去問題】
図に示す5種類の回路は、直流電圧 E[V]の電源と静電容量 C[F]のコンデンサの個数と組み合わせを異にしたものである。これらの回路のうちで、コンデンサ全体に蓄えられている電界のエネルギーが最も小さい回路を示す図として、正しいのは次のうちどれか。
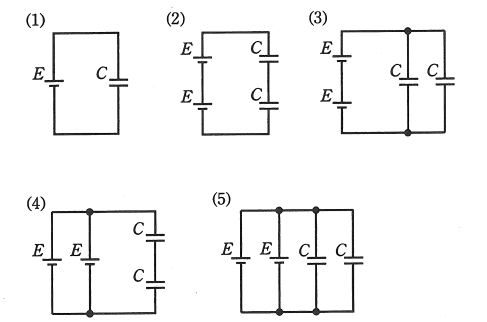
(1) $W=\displaystyle\frac{1}{2}CE^2$
(2) $W=\displaystyle\frac{1}{2}×\frac{C}{2}×(2E)^2=CE^2$
(3) $W=\displaystyle\frac{1}{2}×2C×(2E)^2=4CE^2$
(4) $W=\displaystyle\frac{1}{2}×\frac{C}{2}×E^2=\frac{CE^2}{4}$
(5) $W=\displaystyle\frac{1}{2}×2C×E^2=CE^2$
答え (4)
2011年(平成23年)問2【電験理論の過去問題】
直流電圧 1000[V]の電源で充電された静電容量 8[μF]の平行平板コンデンサがある。コンデンサを電源から外したあとに電荷を保持したままコンデンサの電極間距離を最初の距離の 1/2 に縮めたとき、静電容量[μF]と静電エネルギー[J]の値の組み合わせとして、正しいものを次の(1)~(5)のうちから一つ選べ。
静電容量 静電エネルギー
(1) 16 4
(2) 16 2
(3) 16 8
(4) 4 4
(5) 4 2
平行平板コンデンサの静電容量 $C $[F]は、
$C=ε_0ε_r\displaystyle\frac{S}{d}$
ですので、電極間の距離 $d$ が1/2倍になると、静電容量は倍の16[μF]になります。
$Q=CV$より、$Q$は一定なので極板間隔が1/2になると、電圧$V$は1/2になります。
静電エネルギー $W$[J]は 、
$W=\displaystyle\frac{1}{2}×16×10^{-6}×500^2=2$[J]
答え (2)
2013年(平成25年)問1【電験理論の過去問題】
極板間が比誘電率 $εr$ の誘電体で満たされている平行平板コンデンサに一定の直流電圧が加えられている。このコンデンサに関する記述 a ~ e として、誤っているものの組み合わせを次の(1)~(5)のうちから一つ選べ。
ただし、コンデンサの端効果は無視できるものとする。
- 極板間の電界分布は $εr$ に依存する。
- 極板間の電位分布は $εr$ に依存する。
- 極板間の静電容量は $εr$ に依存する。
- 極板間に蓄えられる静電エネルギーは $εr$ に依存する。
- 極板上の電荷(電気量)は $εr$ に依存する。
- a,b
- a,e
- b,c
- a,b,d
- c,d,e
電圧 $V$ と電界 $E$ の関係式は、
$V=Ed$
極板間の電界分布、極板間の電位分布共に、$εr$ に依存しません。よって、a,bは誤りです。
静電容量 $ C$ は、
$C=\displaystyle\frac{ ε_{ 0 } εrS}{ d }$
ですので、$εr$ に依存します。
静電エネルギー $W$ は 、
$W=\displaystyle\frac{1}{2}CV^2=\displaystyle\frac{1}{2}×\displaystyle\frac{ ε_{ 0 } εrS}{ d }×V^2$
ですので、$εr$ に依存します。
電気量 $ Q$ は、
$Q=CV=\displaystyle\frac{ ε_{ 0 }εr S}{ d }×V$
ですので、$εr$ に依存します。
答え (1)
2015年(平成27年)問2【電験理論の過去問題】
図のように、真空中で2枚の電極を平行に向かい合せたコンデンサを考える。各電極の面積を $A$[m2]、電極の間隔を $l$[m]とし、端効果を無視すると、静電容量は( ア )[F]である。このコンデンサに直流電圧源を接続し、電荷 $Q$[C]を充電してから電圧源を外した。このとき、電極間の電界 $E=$( イ )[V/m]によって静電エネルギー $W=$( ウ )[J]が蓄えられている。この状態で電極間隔を増大させると静電エネルギーも増大することから、二つの電極間には静電力の( エ )が働くことが分かる。
ただし、真空の誘電率を $ε_0$[F/m]とする。
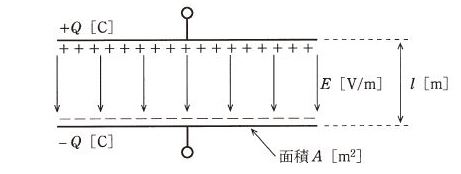
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

静電容量 $ C$ は、
$C=\displaystyle\frac{ ε_{ 0 } A}{ l }$・・・(ア)
電気量 $ Q$ は、
$Q=CV$
電圧 $V$ と電界 $E$ の関係式は、
$V=Ed$
$E=\displaystyle\frac{ V}{ d }=\displaystyle\frac{ \displaystyle\frac{ Q}{ C }}{ \displaystyle\frac{ C}{ ε_{ 0 } A } }=\displaystyle\frac{ Q}{ ε_{ 0 } A }$・・・(イ)
静電エネルギー $W$ は 、
$W=\displaystyle\frac{1}{2}CV^2=\displaystyle\frac{1}{2}×\displaystyle\frac{ Q^2}{ C }=\displaystyle\frac{Q^2l}{2ε_{ 0 } A}$・・・(ウ)
+の電気と-の電気は引き合うので「引力」が(エ)に入ります。
答え (2)
2017年(平成29年)問2【電験理論の過去問題】
極板の面積 $S$[m2]、極板間の距離 $d$[m]の平行板コンデンサ A、極板の面積 $2S$[m2]、極板間の距離 $d$[m]の平行板コンデンサ B 及び極板の面積 $S$[m2]、極板間の距離 $2d$[m]の平行板コンデンサ C がある。各コンデンサは、極板間の電界の強さが同じ値となるようにそれぞれ直流電源で充電されている。各コンデンサをそれぞれの直流電源から切り離した後、全コンデンサを同じ極性で並列に接続し、十分時間が経ったとき、各コンデンサに蓄えられる静電エネルギーの総和の値[J]は、並列に接続する前の総和の値[J]の何倍になるか。その倍率として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、各コンデンサの極板間の誘電率は同一であり、端効果は無視できるものとする。
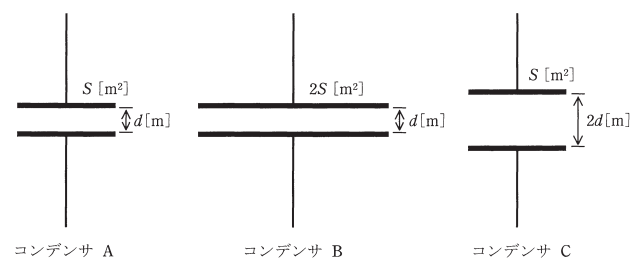
(1) 0.77 (2) 0.91 (3) 1.00 (4) 1.09 (5) 1.31
誘電率 $ε$[F/m]、極板間距離 $d$[m]、極板面積 $S$[m2]のコンデンサ容量 $C$[F]は、
$C=\displaystyle\frac{εS}{d}$
なので、コンデンサ A,B,C の静電容量をそれぞれ $C_A$[F],$C_B$[F],$C_C$[F] とすると、
$C_A=\displaystyle\frac{εS}{d}$,$C_B=\displaystyle\frac{ε2S}{d}=2C_A$ ,$C_C=\displaystyle\frac{εS}{2d}=\displaystyle\frac{1}{2}C_A$
各コンデンサは、極板間の電界の強さが同じ値となるように充電されていますので、コンデンサ A、B、C の電界の強さは等しくなります。電界の強さを $E$[V/m]とし、コンデンサ A、B、C の電圧をそれぞれ $V_A$[V],$V_B$[V],$V_C$[V]とすると、電圧と電界の関係式 $V=Ed$[V]より、
$V_A=Ed$,$V_B=Ed$,$V_C=2Ed$
コンデンサ A,B,C に蓄えられる電荷をそれぞれ $Q_A$[C],$Q_B$[C],$Q_C$[C] とすると、コンデンサに蓄えられる電荷は $Q=CV$[C]ですので、
$Q_A=C_AV_A=C_AEd$
$Q_B=C_BV_B=2C_AEd$
$Q_C=C_CV_C=\displaystyle\frac{1}{2}C_A×2Ed=C_AEd$
コンデンサ A,B,C に蓄えられる静電エネルギーをそれぞれ $W_A$[J],$W_B$[J],$W_C$[J] とすると、各コンデンサをそれぞれの直流電源から切り離した直後の静電エネルギーの総和の値 $W_1$[J]は、
$\begin{eqnarray}W_1 &=& W_A+W_B+W_C \\\\&=& \displaystyle\frac {Q_A^{2}}{2C_A}+\displaystyle\frac {Q_B^{2}}{2C_B}+\displaystyle\frac {Q_C^{2}}{2C_C}\\\\&=& \displaystyle\frac {1}{2}\left(\displaystyle\frac {(C_AEd)^{2}}{C_A}+\displaystyle\frac {(2C_AEd)^{2}}{2C_A}+\displaystyle\frac {(C_AEd)^{2}}{\displaystyle\frac {1}{2}C_A} \right)\\&=& \displaystyle\frac {1}{2}(C_AE^{2}d^{2}+2C_AE^{2}d^{2}+2C_AE^{2}d^{2})\\\\&=& \displaystyle\frac {5}{2}C_AE^{2}d^{2}\end{eqnarray}$
コンデンサを並列接続したときの合計電荷量を $Q_2$[C]、合成静電容量を $C_2$[F]とすると、
$Q_2=Q_A+ Q_B+Q_C=C_AEd+C_AEd+2C_AEd=4C_AEd$
コンデンサを並列接続した場合の合成静電容量 C[F]は、
$C_2=C_A+C_B+C_C=C_A+2C_A+\displaystyle\frac{1}{2}C_A=\displaystyle\frac{7}{2}C_A$
並列接続後の静電エネルギーの総和の値 $W_2$[J]は、
$W_2=\displaystyle\frac{1}{2}\displaystyle\frac{Q_2^{2}}{C_2}=\displaystyle\frac{1}{2}\displaystyle\frac{(4C_AEd)^{2}}{\displaystyle\frac{7}{2}C_A}=\displaystyle\frac {16}{7}C_AE^{2}d^{2}$
並列接続後の静電エネルギーは、並列接続前の何倍になるかを求めます。
$\displaystyle\frac{W_2}{W_1}=\displaystyle\frac{\displaystyle\frac {16}{7}C_AE^{2}d^{2}}{\displaystyle\frac {5}{2}C_AE^{2}d^{2}}≒0.91$
答え (2)
電験三種の理論科目に出題される「静電気分野」のページ
1.クーロンの法則とは
2.電界とガウスの法則
3.静電界中の電位と電圧
4.静電誘導と誘電分極
5.平行平板コンデンサの静電容量
6.コンデンサの直列接続と並列接続
7.静電エネルギー
8.誘電体とコンデンサ
9.導体球と同心球導体の静電容量






