第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「電界とガウスの法則」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「電界とガウスの法則」の過去問題も解説しています。
電界(電場)とは?
電荷の近くに他の電荷を置くと、クーロンの法則で表されるとおり、静電気力が働きます。このように電荷に対して電気的な力が働く場所を「電界」または「電場」といいます。
電界は大きさと向きを持つベクトルで表され、その強さは $E$[V/m]で表します。$E$[V/m]の電界中では、$q$[C]の電荷は $qE$[N]の力を受けます。
電界 $E$ 中に置かれた電荷 $q$ に働く力 $F$ を求める公式
$F=qE$[N]
$F$[N]:電荷 $q$ に働く力(単位はニュートン)
$q$[C]:電荷(単位はクーロン)
$E$[V/m]:電界の強さ(単位はボルト毎メートル)
正の電荷は電界と同じ向き、負の電荷は電界と逆向きに力を受けます。
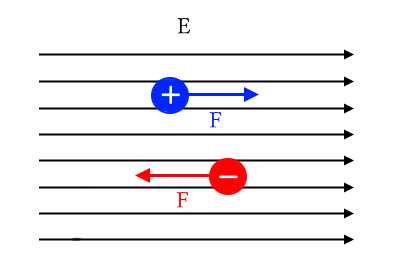
電界の強さ $E$[V/m]中に +1[C]の点電荷を置いたとき、この正の点電荷が受ける静電気力の大きさと向き $F$[N]は電界の強さ $E$[V/m]と同じ値になります。これは、電界(電場)の大きさの定義です。
電界は、地表における重力の考え方と似ています。地球表面の重力場から受ける力 $F$[N]を表す式は、ニュートンの運動方程式より
$F= m(物体の質量)× g(重力加速度)$
と表されます。これを場という考え方で関連させると、物体の質量 $m$ は、重力場が発生した原因の質量に対応している物理量と考えることができ、クーロンの法則で表される、静電気力を発生させる物理量である電荷 $q$[N]と関連できます。
重力加速度 $g$ は、どんな質量の物体でも共通な値で、重力場の状態を表している値と考えることができ、電場(電界)の強さ $E$ と対応していることがわかります。
一様な電界と点電荷が作る電界
電界には「一様な電界」と「点電荷が作る電界」の二通りの考え方があります。電界には大きさと向きがありますので、それぞれの電界がどのようになるのかイメージしましょう。
一様な電界とは?
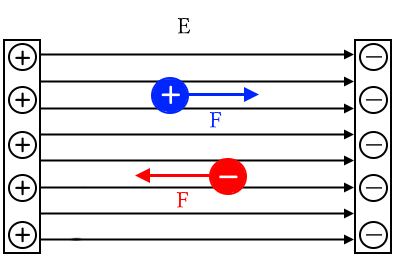
一様な電界とは、大きさと向きがどの場所でも同じ電界です。図のように、仮想的に平行になっている電界と考えてください。
このような正電荷と負電荷が作る電界は、周りに広がらないと考えます。その電界中は、どこでも強さが一定であり、向きも同じと考えることができますので、「一様な電界」といいます。
(正確には平行極板などが作る一様な電界の一番端っこ部分は、端効果で電界が強くなります。端効果については、電験3種では考えなくてもいいです。)
たとえば、コンデンサのように電極の板を平行に置いて、プラスとマイナスをかけると、その間の空間では、電極に垂直の向きにほぼ一様な電界が発生します。
点電荷が作る電界とは?
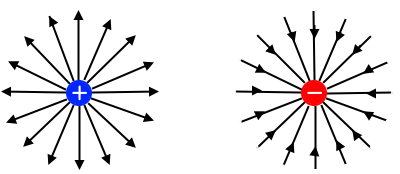
正の点電荷のまわりの電界は、電荷から外側へ放射線状に広がる向きになります。負の点電荷のまわりの電界は、外側から電荷へ放射線状に集まる向きになります。図のような電界を「点電荷が作る電界」といいます。
点電荷 $Q$[C]の $r$[m]離れた地点における、電界の強さ $E$[V/m]は次の式で表すことができます。
点電荷が作る電界の強さ $E$ を求める公式
$E=\displaystyle \frac{ 1 }{ 4πε_{ 0 } }\frac{ Q }{ r^2}$
$E$[V/m]:電界の強さ
$ε_0$:真空の誘電率
$Q$[C]:電荷
$r$[m]:電荷からの距離
電界の強さを表す式はクーロンの法則の式によく似ています。電荷 $Q$[C]の $r$[m]離れた地点に電荷量 1[C]の正の電荷を置いたとき、この正の電荷が受ける静電気力の大きさ $F$ と電界の強さ $E$ は同じ値になります。
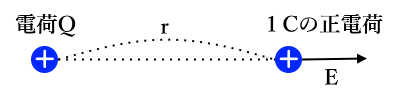
つまり、$F=qE$[N]は一様な電界でも点電荷が作る電界でも、成立します。
二つ以上の電荷が作る電界
図のように二つの電荷 $Q_1$[C],$Q_2$[C]によって点Cに発生する電界を考えます。ただし、$Q_1$[C],$Q_2$[C]はいずれも正電荷とします。電界は、力学で学ぶ力と同様にベクトルで、ベクトルの和が合力となります。C点での $Q_1$ による電界を $E_1$[V/m]、$Q_2$ による電界を $E_2$[V/m]とすると、ベクトルの合成より平行四辺形の対角線が $Q_1$ と $Q_2$ による点Cにおける電界 $E$[N]となります。
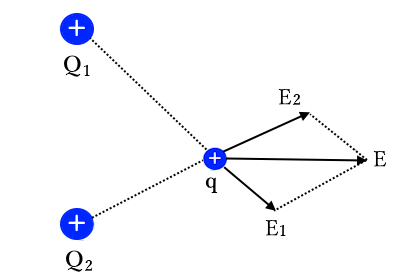
電気力線とガウスの法則
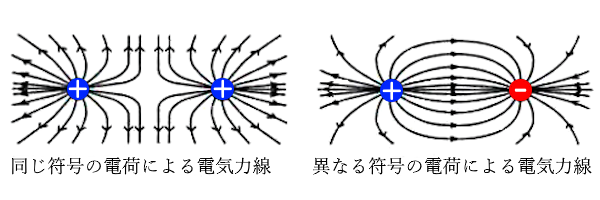
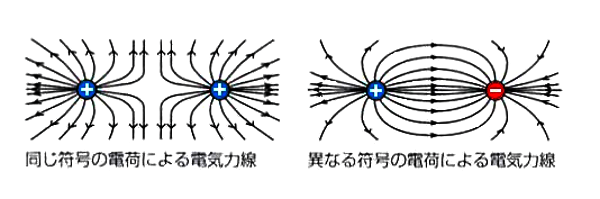
電界をわかりやすく表現するための仮想的な線を「電気力線」といいます。電気力線は正の電荷から出て、負の電荷に入ります。電荷が二つある場合の電気力線は上図のようになります。図は平面で描かれていますが、立体的に捉えてください。
電気力線の特徴は次のようになります。
- 電気力線は正の電荷から出て、負の電荷に入ります。
- 電気力線の接線の方向は、その点での電界の方向です。
- 電気力線は途中で折れ曲がったり、枝分かれしたり、交わることはありません。
- 電界の強いところほど、電気力線は密になります。
- 電気力線の密度と電界の強さは一致しています。
電気力線の本数
電荷の周りには、電気力線が存在すると考えられ、その電気力線の数を求める公式は次のようになります。
真空中に置かれた電荷 $Q$ から出入りする電気力線の数を求める公式
$ N=\displaystyle \frac{ Q }{ ε_{ 0 } }$[本]
$N$[本]:電荷から出る電気力線の数
$Q$[C]:電荷
$ε_o$[F/m]:真空の誘電率
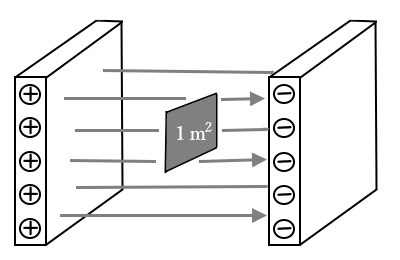
電気力線の特徴より、「電気力線の密度と電界の強さは一致する」とあります。これは、電界の強さが $E$[V/m]のところは、1m2(単位面積)当たり $E$[本]の電気力線があると考えます。
電気力線の特徴に、「電界の強いところほど、電気力線は密になる」とあります。つまり、単位面積あたりの電気力線の本数が多いほど、電界は強いといえます。
ガウスの法則
真空中に点電荷 $Q$[C]がある場合、半径 $r$[m]離れた地点における電気力線の本数から、電界の強さを考えてみます。
点電荷 $Q$[C]から出る電気力線は、点電荷の周囲から球状に出ています。半径 $r$[m]の球の表面積は $4πr^2$[m2]ですので、点電荷 $Q$ から出る全電気力線は $4πr^2$ の球面を貫くことになります。
単位面積あたりの電気力線数は、[電気力線の総数]÷[球の表面積]ですので、
$\displaystyle \frac{ Q }{ ε_{ 0 } }×\frac{ 1 }{ 4πr^2 }$[本]
単位面積当たりの電気力線は $E$[本]$= E$[V/m]です。
$E=\displaystyle \frac{ 1 }{ 4πε_{ 0 } }\frac{ Q }{ r^2}$
点電荷が作る電界の強さの公式と一致します。このように電気力線が貫く面の面積と電気力線の総数から電界の強さを導き出す考え方を「ガウスの法則」といい、任意の立体でこの考え方を使うことができます。
電束と電束密度
電束は電気力線と同様に、電界の力の様子を表すのに使われる仮想の曲線です。電束は電気力線と似ていますが、次のような違いがあります。
- 電気力線の数は、物質の誘電率によって変化する
- 電束の数は、物質の誘電率によって変化しない
電荷と電束の関係として、$Q$ [C] の電荷からは $Q$ の電束が出入りするという決まりがあります。
- 電荷 $Q$ の物質からは $Q$ の電束が出入りする
- 電荷 $Q$ の物質からは $ \displaystyle \frac{ Q }{ ε_{ 0 } }$ 本 の電気力線が出入りする
電束密度
単位面積あたりの電束を「電束密度」といいます。 つまり、1m2 あたりの電束の数のことです。ちなみに、単位面積あたりの電気力線の本数を「電気力線密度」といい、電気力線密度は電界の強さと等しい関係にあります。
電束密度 $D$[C/m2] は、次の式で求めることができます。
平等電界中の電束密度 $D$ を求める公式
$D=\displaystyle \frac{ Q }{ S}$
$D$[C/m2]:電束密度
$Q$[C]:電束
$S$[m2]:電束が通過する面積
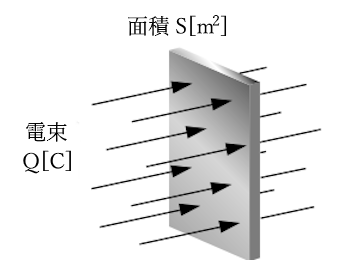
電荷 $Q$ から $r$ 離れた地点における電束密度 $D$ を求める公式
$D=\displaystyle \frac{ Q }{4πr^2}$
$D$[C/m2]:電束密度
$Q$[C]:電荷
$r$[m]:電束が通過する面積
誘電率 $ε$、電界の強さ $E$ のときの、電束密度 $D$ を求める公式
$D=εE$
$D$[C/m2]:電束密度
$ε$[F/m]:誘電率
$E$[V/m]:電界の強さ
電験三種-理論の過去問解説:電界とガウスの法則
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2008年(平成20年)問1【電験理論の過去問題】
真空中において、図のように一辺が 2a[m]の正三角形の各頂点A,B,Cに正の点電荷 Q[C]が配置されている。点Aから辺BCの中点Dに下ろした垂線上の点Gを正三角形の重心とする。点Dから x[m]離れた点Pの電界[V/m]の大きさを表わす式として、正しいのは次のうちどれか。
ただし,点Pは点Dと点G間の垂線上にあるものとし,真空の誘電率を ε0[F/m]とする。
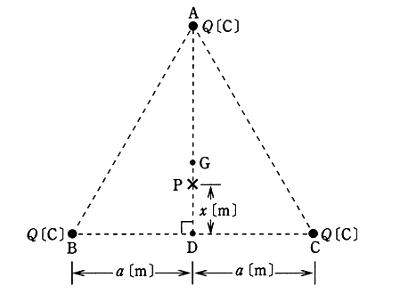
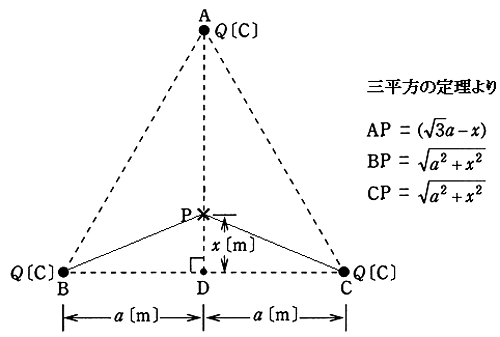
AD間の距離は $\sqrt{ 3 }a$ ですので、P点におけるA点の点電荷による電界の強さを $E_{ A }$ [V/m]とすると、
$ E_{ A }=\displaystyle \frac{ 1 }{ 4πε_{ 0 } }×\frac{ Q }{ (\sqrt{ 3 }a-x)^2}$
P点におけるB点及びC点の点電荷による電界の強さをそれぞれ $E_{ B }$ 、$E_{ C }$ [V/m]とすると、
$ E_{ B }=E_{ C }=\displaystyle \frac{ 1 }{ 4πε_{ 0 } }×\frac{ Q }{ (\sqrt{ a^2+x^2})^2}$
電界の強さを $E_{ A }$、$ E_{ B }$、$E_{ C }$をベクトル図で表すと下図のようになります。

合成電界 EBC[V/m]は
$\begin{eqnarray}E_{ BC }&=&E_{ B }cosθ\\\\&=&\displaystyle \frac{ x }{ \sqrt{ a^2+x^2}}×\displaystyle \frac{ Q }{ 4πε_{ 0 } (\sqrt{ a^2+x^2})^2}\\\\&=&\displaystyle \frac{ Q }{ 4πε_{ 0 }}× \frac{ x }{(\ a^2+x^2)^\frac{ 3 }{ 2 }}\end{eqnarray}$
点 P の電界の強さを E[V/m]は
$\begin{eqnarray}E&=&E_{ A }-2E_{ B }\\\\&=&\displaystyle \frac{ 1 }{ 4πε_{ 0 } }×\frac{ Q }{ (\sqrt{ 3 }a-x)^2}-2×\displaystyle \frac{ Q }{ 4πε_{ 0 }}× \frac{ x }{(\ a^2+x^2)^\frac{ 3 }{ 2 }}\\\\&=&\displaystyle \frac{ Q }{ 4πε_{ 0 }}\biggl( { \frac{ 1 }{(\sqrt{ 3 } a-x)^2 }}-\frac{ 2x }{(\ a^2+x^2)^\frac{ 3 }{ 2 }}\biggl)\end{eqnarray}$
答え (5)
2007年(平成19年)問3【電験理論の過去問題】
図に示すように、誘電率 ε0[F/m]の真空中に置かれた静止した二つの電荷 A[C]及び B[C]があり、図中にその周囲の電気力線が描かれている。電荷 A=16ε0[C]であるとき、電荷 B[C]の値として、正しいのは次のうちどれか。
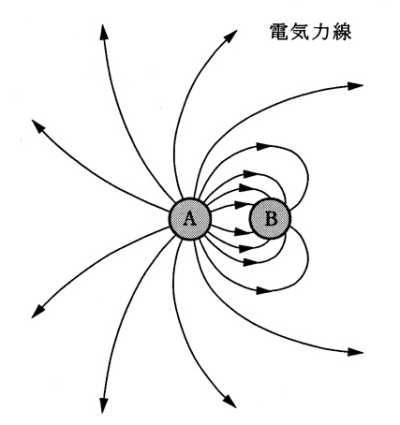
(1) 16ε0 (2) 8ε0 (3) -4ε0 (4) -8ε0 (5) -16ε0
電荷 A=16ε0[C]からは、16本の電気力線が出ています。問題の図は電荷Aから出た電気力線のうち8本が電荷Bに入っているので、Bの電荷は B=-8ε0[C]となります。
答え (4)
2010年(平成22年)問17【電験理論の過去問題】
真空中において、図に示すように、一辺の長さが 6[m]正三角形の頂点Aに 4×10-9[C]の正の点電荷が置かれ、頂点Bに -4×10-9[C]の負の点電荷が置かれている。正三角形の残る頂点を点Cとし、点Cより下ろした垂線と正三角形の辺ABとの交点を点Dとして、次の(a)及び(b)の問に答えよ。
ただし、クーロンの法則の比例定数を 9×109[N・m2/C2]とする。
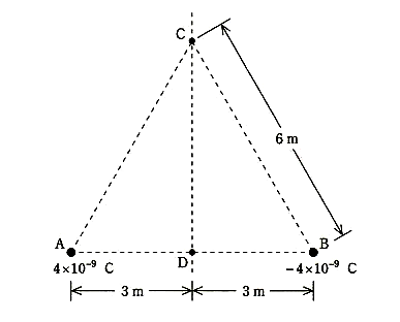
(a) まず、q0[C]の正の点電荷を点Cに置いたときに、この正の点電荷に働く力の大きさは FC[N]であった。次にこの正の点電荷を点Dに移動したときに、この正の点電荷に働く力の大きさは FD[N]であった。力の大きさの比 $\displaystyle \frac{ F_C }{ F_D}$ の値として、正しいのは次のうちどれか。
(1) $\displaystyle \frac{1}{ 8}$ (2) $\displaystyle \frac{1}{4}$ (3) 2 (4) 4 (5) 8
(b) 次に、$q_0$[C]の正の点電荷を点Dから点Cの位置に戻し、強さが $0.5$[V/m]の一様な電界を辺ABに平行に点Bから点Aの向きに加えた。このとき、$q_0$[C]の正の点電荷に電界の向きと逆の向きに $2×10^{-9}$[N]の大きさの力が働いた。正の点電荷 $q_0$[C]の値として、正しいのは次のうちどれか。
(1) $\displaystyle \frac{4}{3}$×10-9 (2) 2×10-9 (3) 4×10-9 (4) $\displaystyle \frac{ 4 }{ 3}$×10-8 (5) 2×10-8
(a) q0[C]の正の点電荷を点Cに置いたときと、正の点電荷を点Dに移動したときの働く力の大きさを図に示します。クーロンの法則の比例定数を k と置けば、
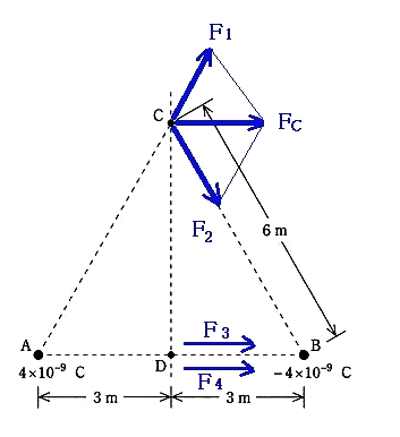
$F_1=k\displaystyle \frac{ Q_1Q_2}{ r^2}=k×\displaystyle \frac{ 4×10^{-9}×q_0}{ 6^2}$
$F_2=k\displaystyle \frac{ Q_1Q_2}{ r^2}=k×\displaystyle \frac{ 4×10^{-9}×q_0}{ 6^2}$
$F_3=k\displaystyle \frac{ Q_1Q_2}{ r^2}=k×\displaystyle \frac{ 4×10^{-9}×q_0}{ 3^2}$
$F_4=k\displaystyle \frac{ Q_1Q_2}{ r^2}=k×\displaystyle \frac{ 4×10^{-9}×q_0}{ 3^2}$
F1=F2ですので、FC=F1=F2 となります。
$F_C=k×\displaystyle \frac{ 4×10^{-9}×q_0}{ 6^2}$
FD=F3+F4 ですので、
$F_D=k×\displaystyle \frac{ 2×4×10^{-9}×q_0}{ 3^2}$
したがって、$\displaystyle \frac{ F_C }{ F_D}$ は、
$\displaystyle \frac{ F_C }{ F_D}=\displaystyle \frac{ k×\displaystyle \frac{ 4×10^{-9}×q_0}{ 6^2} }{ k×\displaystyle \frac{ 2×4×10^{-9}×q_0}{ 3^2}}=\displaystyle \frac{ 1 }{ 8}$
答え (1)
(b) 問題文を図示します。
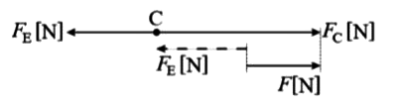
$F_C=9×10^9×\displaystyle \frac{ 4×10^{-9}×q_0}{ 6^2}=q_0$
FE の力は、F=qE より
$F_E=q_0×0.5$
$F=F_C-F_E$
$2×10^{-9}=q_0-0.5q_0$
$q_0=4×10^{-9}$
答え (3)
2017年(平成29年)問1【電験理論の過去問題】
電界の状態を仮想的な線で表したものを電気力線という。この電気力線に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- 同じ向きの電気力線同士は反発し合う。
- 電気力線は負の電荷から出て、正の電荷へ入る。
- 電気力線は途中で分岐したり、他の電気力線と交差したりしない。
- 任意の点における電気力線の密度は、その点の電界の強さを表す。
- 任意の点における電界の向きは、電気力線の接線の向きと一致する。
電気力線は電界をわかりやすく表現するための仮想的な線です。電界を可視化できるように考えられたもので、次のような特徴があります。
- 電気力線は正の電荷から出て、負の電荷に入ります。
- 電気力線の接線の方向は、その点での電界の方向です。
- 電気力線は途中で折れ曲がったり、枝分かれしたり、交わることはありません。
- 電界の強いところほど、電気力線は密になります。
- 電気力線の密度と電界の強さは一致しています。
したがって、(2)が誤りです。
答え (2)
電験三種の理論科目に出題される「静電気分野」のページ
1.クーロンの法則とは
2.電界とガウスの法則
3.静電界中の電位と電圧
4.静電誘導と誘電分極
5.平行平板コンデンサの静電容量
6.コンデンサの直列接続と並列接続
7.静電エネルギー
8.誘電体とコンデンサ
9.導体球と同心球導体の静電容量




