第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「誘電体とコンデンサ」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「誘電体とコンデンサ」の過去問題も解説しています。
コンデンサの横分割について
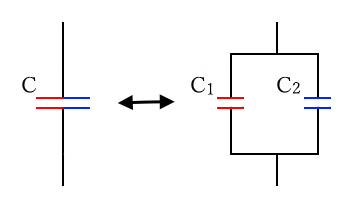
コンデンサを並列接続した場合の合成静電容量は、
$C=C_{ 1 }+C_{ 2 }$
です。この式は、2つのコンデンサの合成静電容量は足し算で合計できるということです。逆をいえば、分割できることも意味しています。
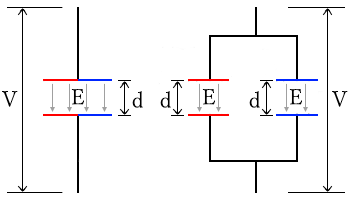
コンデンサが横方向に分割ができるのは、分割前後で電気力線の数が変わらないからです。一様な電界による電圧は $V=Ed$です。
横方向に分割するので、電極間の距離 $d$ は同じです。また、電界の強さが $E$[V/m]のところは、$1m^2$(単位面積)当たり $E$[本]の電気力線があります。
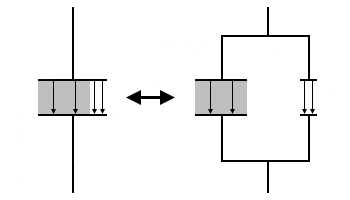
つまり、コンデンサにかかっている電圧が同じなら、電気力線の数は分割前後で変わりません。並列接続の場合は電圧が変わりませんので、このような分割ができるというわけです。
1つのコンデンサ内に誘電率が異なる物質が挿入されている場合でも、横方向の分割は成り立ちます。
平行板コンデンサは電気力線の方向が極板に垂直です。どこで分割しても、電圧が同じなら電気力線はなくなりません。
誘電体を挟んだ部分の電気力線の本数が少ないのは、誘電体が電界を弱めているからです。誘電体が差し込まれると電気力線は減り電気容量は大きくなります。
コンデンサの縦分割について
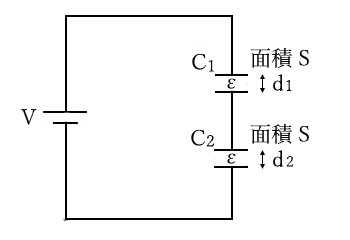
誘電率が $ε$、極板の面積 $S$、極板間の大きさをそれぞれ、$d_1$,$d_2$ の二つのコンデンサ $C_{ 1 }$,$C_{ 2}$ が直列に接続されています。
各コンデンサの静電容量は、次のようになります。
$C_{ 1 }=\displaystyle\frac{ εS}{ d_{ 1 } }$,$C_{ 2 }=\displaystyle\frac{ εS}{ d_{ 2 } }$
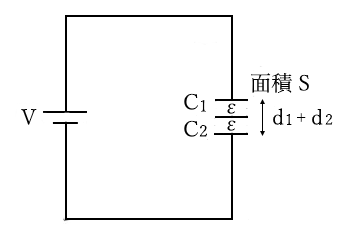
コンデンサ直列回路の合成静電容量より、
$C=\displaystyle\frac{1}{\displaystyle\frac{1}{C_{ 1 }}+\displaystyle\frac{1}{C_{ 2 }}}=\displaystyle\frac{1}{\displaystyle\frac{1}{\displaystyle\frac{ εS}{ d_{ 1 } }}+\displaystyle\frac{1}{\displaystyle\frac{ εS}{ d_{ 2 } }}}=\displaystyle\frac{εS }{ d_{ 1 }+d_{ 2 } }$
誘電率と極板の面積が共通しているコンデンサを直列に接続すると、コンデンサの極板間を大きくすること ($d_{ 1 }+d_{ 2 }$) と同じといえます。
誘電率の異なる誘電体
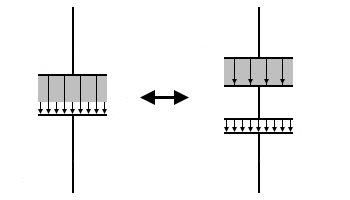
極板間に誘電率の異なる誘電体を直列に挟んだコンデンサについて考えてみます。極板間に挟む誘電体が極板の面積と同じ形なら、電気力線の形が変わらないので図のように分割できます。
順番が変わっても合成静電容量は同じ
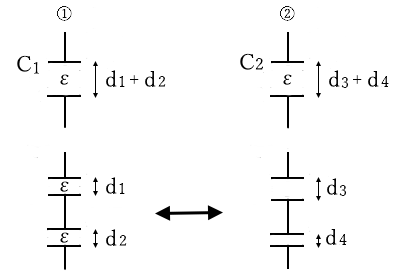
コンデンサは①と②のように分割できますので、$C_{ 1 }=C_{ 2}$ なら、図のようにコンデンサが入れ変わっても合成静電容量は同じになります。
$C_1=C_2$ ⇔ $\displaystyle\frac{εS }{ d_{ 1 }+d_{ 2 } }=\displaystyle\frac{εS }{ d_{ 3 }+d_{ 4 } }$
$\displaystyle\frac{εS }{ d_{ 1 } }+\displaystyle\frac{εS }{ d_{ 2 } }=\displaystyle\frac{εS }{ d_{ 3 }}+\displaystyle\frac{εS }{ d_{ 4 }}$
導体を挟んだコンデンサ
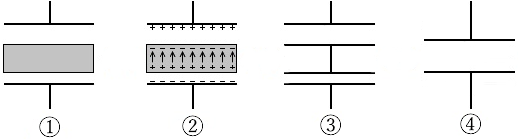
①のように、コンデンサの途中に導体を挟んだ場合、静電誘導により②のように電荷が現れます。導体内部では電界は0になります。つまり③のように導体部分は無いものとみなすことができます。③を合成すると④のようになります。
誘電体を挟んだコンデンサ
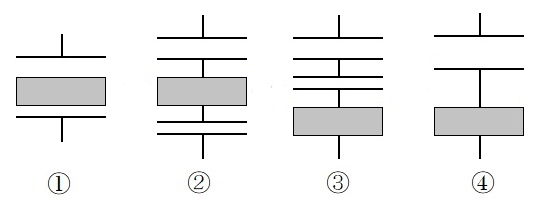
①のように、コンデンサの途中に誘電体を挟んだ場合、②のようにコンデンサを分割できます。コンデンサーは電荷が現れます。コンデンサは順番が変わっても合成静電容量は同じですので、③のように考えることができます。③を合成すると④のようになります。
電験三種-理論の過去問解説:誘電体とコンデンサ
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2002年(平成14年)問1【電験理論の過去問題】
図のように、面積 S[m2]の電極板からなる平行板コンデンサがある。この電極板と平行に同じ形の導体平板を図に示す間隔で入れ、このコンデンサの両端の電極に 120[V]の直流電圧を加えて充電した。このとき、図中の電圧 V0 [V]の値として、正しいのは次のうちどれか。
ただし、電極板間の誘電体の誘電率は同一とし、充電前の電極及び導体平板の初期電荷は零とする。また、電極板及び導体平板の厚さ並びにこれらの端効果は、無視できるものとする。
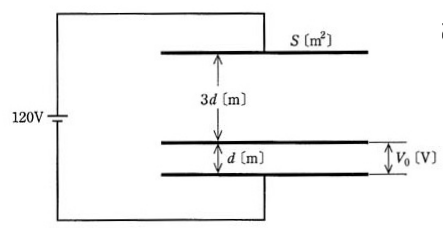
(1) 0 (2) 30 (3) 60 (4) 90 (5) 120
コンデンサーの静電容量は、誘電率をεとすると $C=\displaystyle\frac{ εS}{ d }$[F]ですので、電極間隔 $d$ と $3d$ の静電容量をそれぞれ $C_{ 0 }$、$C$とすれば、
$C_{ 0 }=\displaystyle\frac{ εS}{ d }$
$C=\displaystyle\frac{ εS}{ 3d }$
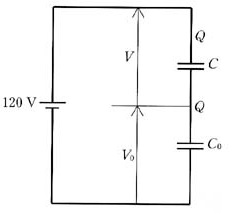
直流回路に蓄えられる電荷 $Q$ は等しいので、
$Q=CV=C_{ 0 }V_{ 0 }$
$V+V_{ 0 }=120$なので、
$C(120-V_{ 0 })=C_{ 0 }V_{ 0 }$
$\displaystyle\frac{ εS}{ 3d }(120-V_{ 0 })=\displaystyle\frac{ εS}{ d }V_{ 0 }$
$(120-V_{ 0 })=3V_{ 0 }$ $V_{ 0 }=30$
答え (2)
2003年(平成15年)問2【電験理論の過去問題】
真空中において、一辺 $l$[m]の正方形電極を間隔 $d$[m]で配置した平行板コンデンサがある。図1はこのコンデンサの電極板間に比誘電率 $ε_{ r }=3$の誘電体を挿入した状態、図2は図1の誘電体を電極面積の 1/2 だけ引き出した状態を示している。図1及び図2の二つのコンデンサの静電容量 $C_{ 1 }$[F]及び $C_{ 2 }$[F]の比($C_{ 1 }:C_{ 2 }$)として、正しいのは次のうちどれか。
ただし、$l>>d$ であり、コンデンサの端効果は無視できるものとする。
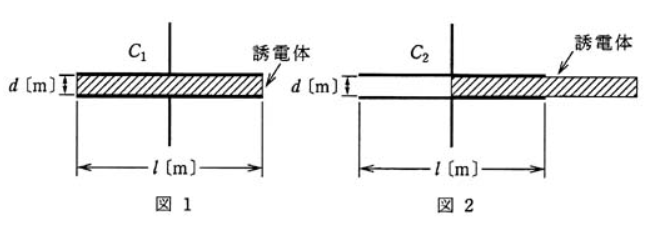
(1) 2:1 (2) 3:1 (3) 3:2 (4) 4:3 (5) 5:4
図1のコンデンサの静電容量は
$C_{ 1 }=\displaystyle\frac{ ε_{ 0 }ε_{ r }l^2}{ d }=\displaystyle\frac{ 3ε_{ 0 }l^2}{ d }$
図2のコンデンサの静電容量は誘電率$ε_{ 0 }$と$ε_{ 0 }ε_{ r }$のコンデンサーが半分ずつ挿入されているので、
$\begin{eqnarray}C_{ 2 }&=&\displaystyle\frac{ ε_{ 0 }×l×\frac{ l}{ 2 }}{ d }+\displaystyle\frac{ ε_{ 0 }ε_{ r }×l×\frac{ l}{ 2 }}{ d }\\\\&=&\displaystyle\frac{ ε_{ 0 }×l^2}{ 2d }+\displaystyle\frac{ 3ε_{ 0 }×l^2}{ 2d }\\\\&=&\displaystyle\frac{ 2ε_{ 0 }l^2}{ d }\end{eqnarray}$
よって
$C_{ 1 }:C_{ 2 }=\displaystyle\frac{ 3ε_{ 0 }l^2}{ d }:\displaystyle\frac{ 2ε_{ 0 }l^2}{ d }=3:2$
答え (3)
2004年(平成16年)問1【電験理論の過去問題】
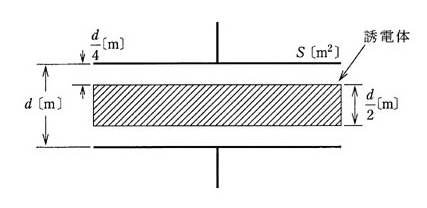
真空中において、面積 $S$[m2]の電極板を間隔 $d$[m]で配置した平行板コンデンサがある。この電極板と同じ形をした厚さ($\frac{ d}{ 2 }$)[m]、比誘電率 2 の誘電体を図に示す間隔で平行に挿入した。このとき、誘電体を挿入する前と比較してコンデンサの静電容量[F]は何倍になるか。その倍率として最も近いのは次のうちどれか。
ただし、電極板の厚さ並びにコンデンサの端効果は、無視できるものとする。
(1) 1.3 (2) 1.5 (3) 2.0 (4) 2.5 (5) 3.0
誘電体を挿入する前の静電容量を $C_{ 1 }$[F]とすると,
$C_{ 1 }=\displaystyle\frac{ ε_{ 0 }S}{ d }$
誘電体を挿入した後の静電容量を $C_{ 2 }$[F]とすると,
$\displaystyle\frac{ 1}{C_{ 2 }}=\displaystyle\frac{ 1}{ \displaystyle\frac{ ε_{ 0 }S}{\displaystyle \frac{ d}{ 2 } }}+\displaystyle\frac{ 1}{\displaystyle\frac{ ε_{ 0 }ε_{ r }S}{ \displaystyle\frac{ d}{ 2 } }}=\displaystyle\frac{ 3d}{4ε_{ 0 }S}$
よって
$C_{ 2 }=\displaystyle\frac{ 4ε_{ 0 }S}{ 3d }=\displaystyle\frac{ 4}{ 3 }C_{ 1 }$
答え (1)
2005年(平成17年)問18【電験理論の過去問題】
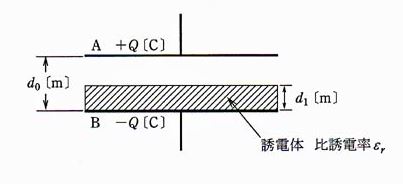
電極板の間隔が $d_0$[m]、電極板面積が十分に広い平行板空気コンデンサがある。このコンデンサの電極板間にこれと同形、同面積の厚さ $d_1$[m]、比誘電率 $ε_r$の誘電体を図のように挿入した。いま、このコンデンサの電極A、Bに $+Q$[C]、$-Q$[C]の電荷を与えた。次の(a)及び(b)に答よ。
ただし、コンデンサの初期電荷は零とし、端効果は無視できるものとする。また、空気の比誘電率は 1 とする。
(a) 空げきの電界 $E_1$[V/m]と誘電体中の電界 $E_2$[V/m]の比 $\displaystyle\frac{ E_1}{ E_2}$を表す式として、正しいものは次のうちどれか。
(1) $ε_r$ (2) $\displaystyle\frac{ ε_rd_1}{ d_0-d_1}$ (3) $\displaystyle\frac{ ε_rd_1^2}{ (d_0-d_1)^2}$ (4) $\displaystyle\frac{ ε_r(d_0-d_1)}{ d_1}$ (5) $\displaystyle\frac{ ε_rd_1}{ d_0}$
(b) 電極板の間隔 $d_0=1.0×10^{-3}$[m]、誘電体の厚さ $d_1=0.2×10^{-3}$[m]及び誘電体の比誘電率 $ε_r=5.0$としたとき、空げきの電界 $E_1=7×10^{4}$[V/m]であった。コンデンサの充電電圧 $V$[V]の値として、正しいのは次のうちどれか。
(1) 100.8 (2) 70.0 (3) 67.2 (4) 58.8 (5) 56.7
(a) 空げきの静電容量を $C_1$[F]と誘電体中の静電容量 $C_2$[F]、電極の面積を $S$[m2]とすると、
$C_1=\displaystyle\frac{ ε_0S}{ d_0-d_1}$
$C_2=\displaystyle\frac{ ε_0ε_rS}{ d_1}$
電界の強さ $E$[V/m]は、$E=\displaystyle\frac{ V}{ d}$ なので、$C_1$, $C_2$ のコンデンサに印加されている電圧をそれぞれ $V_1$,$V_2$[V]とすると、
$E_1=\displaystyle\frac{ V_1}{ d_0-d_1}=\displaystyle\frac{ \displaystyle\frac{ Q}{ C_1}}{ d_0-d_1}=\displaystyle\frac{ \displaystyle\frac{ Q}{ \displaystyle\frac{ ε_0S}{ d_0-d_1}}}{ d_0-d_1}=\displaystyle\frac{ Q}{ ε_0S}$
$E_2=\displaystyle\frac{ V_2}{d_1}=\displaystyle\frac{ \displaystyle\frac{ Q}{ C_2}}{d_1}=\displaystyle\frac{ \displaystyle\frac{ Q}{ \displaystyle\frac{ ε_0ε_rS}{ d_1}}}{d_1}=\displaystyle\frac{ Q}{ ε_0ε_rS}$
したがって、$\displaystyle\frac{ E_1}{ E_2}$ は、
$\displaystyle\frac{ E_1}{ E_2}=\displaystyle\frac{ \displaystyle\frac{ Q}{ ε_0S}}{ \displaystyle\frac{ Q}{ ε_0ε_rS}}=ε_r$
答え (1)
(b) 題意より
$\begin{eqnarray}V&=&E_1(d_0-d_1)+E_2d_1\\\\&=&E_1\left((d_0-d_1)+\displaystyle\frac{E_2}{E_1}d_1\right)\\\\&=&E_1\left((d_0-d_1)+\displaystyle\frac{d_1}{ε_r}\right)\\\\&=&7×10^{4}×\left((1.0×10^{-3}-0.2×10^{-3})+\displaystyle\frac{0.2×10^{-3}}{5.0}\right)\\\\&=&58.8[V]\end{eqnarray}$
答え (4)
2006年(平成18年)問2【電験理論の過去問題】
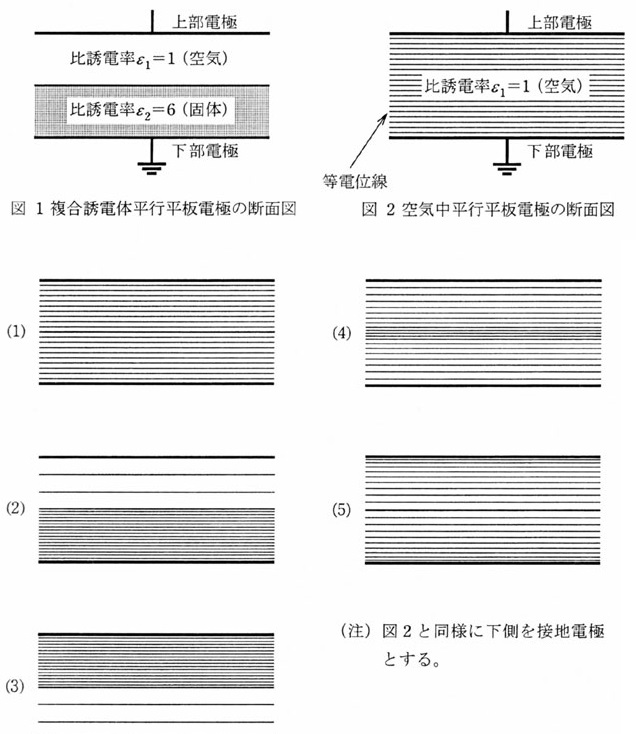
図1に示すような、空気中における固体誘導体を含む複合誘電体平行平板電極がある。この下部電極を接地し、上部電極に電圧を加えたときの電極間の等電位線の分布を示す断面図として、正しいのは次のうちどれか。
ただし、誘電体の導電性及び電極と誘電体の端効果は無視できるものとする。
参考までに固体誘電体を取り除いた、空気中平行平板電極の場合の等電位線の分布を図2に示す。
空気中の静電容量を $C_1$[F]、固体誘電体中の静電容量を $C_2$[F]、電極の面積を $S$[m2]とすると、
$C_{ 1 }=\displaystyle\frac{ ε_{ 0 }S}{ d }$
$C_{ 2 }=\displaystyle\frac{ ε_{ 0 }ε_{ r }S}{ d }=\displaystyle\frac{ 6ε_{ 0 }S}{ d }$
$Q=C_{ 1 }V_{ 1 }=C_{ 2 }V_{ 2 }$ より
$V_{ 1 }=6V_{ 2 }$
$C_{ 1 }$ のコンデンサの電圧は $C_{ 2 }$ の電圧の 6倍ですので,等電位線の密度も 6倍となります。
答え (3)
2009年(平成21年)問1【電験理論の過去問題】
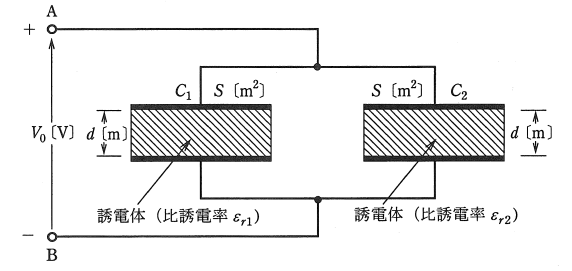
電極板面積と電極板間隔が共に S[m2]と d[m]で、一方は比誘電率が εr1の誘電体からなる平行平板コンデンサ C1 と、他方は比誘電率が εr2 の誘電体からなる平行平板コンデンサ C2 がある。いま、これらを図のように並列に接続し、端子A、B間に直流電圧 V0[V]を加えた。このとき、コンデンサ C1 の電極板間の電界の強さを E1[V/m]、電束密度を D1[C/m2]、また、コンデンサ C2 電極板間の電界の強さを E2[V/m]、電束密度を D2[C/m2]とする。両コンデンサの電界の強さ E1[V/m]と E2[V/m]はそれぞれ( ア )であり、電束密度 D1[C/m2]と D2[C/m2]はそれぞれ( イ )である。したがって、コンデンサ C1 に蓄えられる電荷を Q1[C]、コンデンサ C2 に蓄えられる電荷を Q2[C]とすると、それらはそれぞれ( ウ )となる。
ただし、電極板の厚さ及びコンデンサの端効果は、無視できるものとする。また、真空の誘電率を ε0[F/m]とする。
上記の記述中の空白個所(ア),(イ)及び(ウ)に当てはまる式として、正しいものを組み合わせたのは次のうちどれか。

- 電界(電場)の強さ E=V/d[V/m]
- 電束密度 D=εE[C/m2]
- 電荷 Q=CV[C]
- 静電容量 C=εS/d[F]
以上の公式を当てはめると(4)が正解になります。
答え (4)
2009年(平成21年)問17【電験理論の過去問題】
図に示すように、面積が十分に広い平行平板電極(電極間距離 10[mm])が空気(比誘電率 εr1=1 とする。)と、電極と同形同面積の厚さ 4[mm]で比誘電率 εr2=4 の固体誘電体で構成されている。下部電極を接地し、上部電極に直流電圧 V[kV]を加えた。次の(a)及び(b)に答えよ。
ただし、固体誘電体の導電性及び電極と固体誘電体の端効果は無視できるものとする。
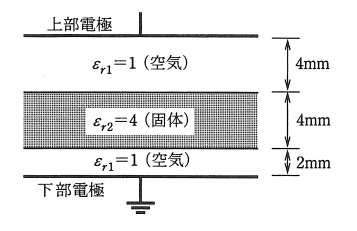
(a) 電極間の電界の強さ E[kV/mm]のおおよその分布を示す図として、正しいのは次のうちどれか。
ただし、このときの電界の強さでは、放電は発生しないものとする。また、各図において、上部電極から下部電極に向かう距離を x[mm]とする。
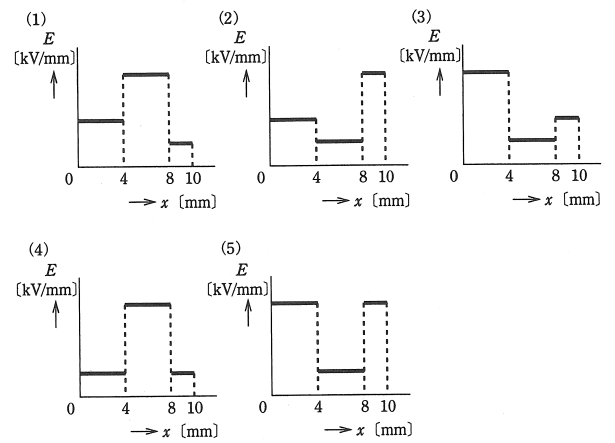
(b) 上部電極に加える電圧 V[kV]を徐々に増加し、下部電極側の空気中の電界の強さが 2[kV/mm]に達したときの電圧 V[kV]の値として、正しいのは次のうちどれか。
(1) 11 (2) 14 (3) 20 (4) 44 (5) 56
(a) 電束密度を D、空気間の電界を $E_1$、固体誘電体間の電界を $E_2$ とすると、電場の関係式は、$D=εE$ ですので、
$E_1=\displaystyle\frac{ D}{ ε_{r1}ε_0 }=\displaystyle\frac{ D}{ ε_0 }$
$E_2=\displaystyle\frac{ D}{ ε_{r2}ε_0 }=\displaystyle\frac{ D}{ 4ε_0 }=\displaystyle\frac{ E_1}{ 4 }$
これを満たすグラフは(5)しかありません。
答え (5)
(b) 電界の強さ $E$ と電圧の関係 $V$ は、$ V=Ed$ です。3つのコンデンサが、直列に接続されたとみなし、各コンデンサの両端にかかる電圧をそれぞれ、$V_1$,$V_2$,$V_3$[V]とすると、印加された電圧は $ V=V_1+V_2+V_3$ となりますので、
$ \begin{eqnarray}V &=& V_1+V_2+V_3\\\\&=& E_1×4+E_2×4+E_1×2\\\\&=& 6E_1+4E_2\\\\&=& 6E_1+4×\displaystyle\frac{ E_1}{ 4 }\\\\&=& 7E_1\end{eqnarray}$
下部電極側の空気中の電界の強さが 2[kV/mm]に達したというのは、$E_1$が 2[kV/mm]に達したときですので、
$V=7E_1=7×2=14$[kV]
答え (2)
2012年(平成24年)問2【電験理論の過去問題】
極板A-B間が誘電率 $ε_0 $[F/m]の空気で満たされている平行平板コンデンサの空気ギャップ長を $d $[m]、静電容量を $C_0$[F]とし、極板間の直流電圧を $V_0$[V]とする。極板と同じ形状と面積を持ち、厚さが $\displaystyle\frac{ d}{ 4 }$[m]、誘電率 $ε_1$[F/m]の固体誘電体($ε_1$>$ε_0$)を図に示す位置P-Q間に極板と平行に挿入すると、コンデンサ内の電位分布は変化し、静電容量は $C_1$[F]に変化した。このとき、誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし、空気の誘電率を $ε_0$、コンデンサの端効果は無視できるものとし、直流電圧 $V_0$[V]は一定とする。
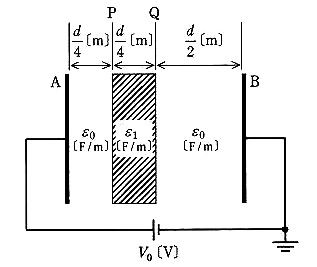
- 位置Pの電位は、固体誘電体を挿入する前の値よりも低下する。
- 位置Qの電位は、固体誘電体を挿入する前の値よりも上昇する。
- 静電容量 $C_1$[F]は、$C_0$[F]よりも大きくなる。
- 固体誘電体を導体に変えた場合、位置Pの電位は固体誘電体又は導体を挿入する前の値よりも上昇する。
- 固体誘電体を導体に変えた場合の静電容量 $C_2$[F]は、$C_0$[F]よりも大きくなる。
極板AおよびBに電荷密度 $σ$[C/m2]の電荷が蓄えられたとします。極板AB 間の電束密度は、$D=σ$[C/m2]ですので、ギャップ部分の電界を $E_0$[V/m]、固体誘電体部分の電界を $E_1$[V/m]とすると、
$E_0=\displaystyle\frac{ D}{ ε_0 }=\displaystyle\frac{ σ}{ ε_0 }$[V/m]
$E_1=\displaystyle\frac{ D}{ ε_1 }=\displaystyle\frac{ σ}{ ε_1 }$[V/m]
極板間の直流電圧を $V_0$[V]は、電位差として表すことができますので
$\begin{eqnarray}V_0&=&E_0×\displaystyle\frac{ d}{ 2 }+E_1×\displaystyle\frac{ d}{ 4 }+E_0×\displaystyle\frac{ d}{ 4 }\\\\&=&\displaystyle\frac{ 3}{ 4 }E_0d+\displaystyle\frac{ 1}{ 4 }E_1d\\\\&=&\displaystyle\frac{ 3}{ 4 }×\displaystyle\frac{ σ}{ ε_0 }×d+\displaystyle\frac{ 1}{ 4 }×\displaystyle\frac{ σ}{ ε_1 }×d\\\\&=&\displaystyle\frac{ σd}{ ε_0 }\left(\displaystyle\frac{ 3}{ 4 }+\displaystyle\frac{ ε_0}{ 4ε_1 }\right)[V]\end{eqnarray}$
$σ=\displaystyle\frac{ ε_0}{ \displaystyle\frac{ 3}{ 4 }+\displaystyle\frac{ ε_0}{ 4ε_1 }}\displaystyle\frac{ V_0}{ d }$[C/m2]
したがって、
$E_0=\displaystyle\frac{ σ}{ ε_0 }=\displaystyle\frac{ 1}{ \displaystyle\frac{ 3}{ 4 }+\displaystyle\frac{ ε_0}{ 4ε_1 }}\displaystyle\frac{ V_0}{ d }$[V/m]
$E_1=\displaystyle\frac{ σ}{ ε_1 }=\displaystyle\frac{ \displaystyle\frac{ ε_0}{ ε_1 }}{ \displaystyle\frac{ 3}{ 4 }+\displaystyle\frac{ ε_0}{ 4ε_1 }}\displaystyle\frac{ V_0}{ d }$[V/m]
固体誘電体を挿入する前の位置P、位置Qの電位を $V_{P0}$[V]、$V_{Q0}$[V]とすると、
$V_{P0}=\displaystyle\frac{ 3}{ 4}V_0$[V]
$V_{Q0}=\displaystyle\frac{ 1}{ 2}V_0$[V]
固体誘電体を挿入した後の位置Pの電位を $V_{P1}$[V]とすると、
$\begin{eqnarray}V_{P1}&=&V_0-E_0×\displaystyle\frac{ d}{ 4}\\\\&=&V_0-\displaystyle\frac{ 1}{ 3+\displaystyle\frac{ ε_0}{ ε_1 }} V_0\\\\&=&\displaystyle\frac{ 2+\displaystyle\frac{ ε_0}{ ε_1 }}{ 3+\displaystyle\frac{ ε_0}{ ε_1 }} V_0[V]\end{eqnarray}$
$ε_1>ε_0 $なので、$V_{P1}>V_{P0}$ となりますので、(1)は正しい記述です。
固体誘電体を挿入した後の位置Qの電位を$V_{Q1}$[V]とすると、
$\begin{eqnarray}V_{Q1}&=&E_0×\displaystyle\frac{ d}{ 2}\\\\&=&\displaystyle\frac{ 1}{ \displaystyle\frac{ 3}{ 4 }+\displaystyle\frac{ ε_0}{ 4ε_1 }}\displaystyle\frac{ V_0}{ 2 }[V]\end{eqnarray}$
$ε_1>ε_0 $なので、$V_{Q1}>V_{Q0}$ となりますので、(2)は正しい記述です。
固体誘電体を挿入する前の静電容量を $C_0$[F]は、
$C_0=ε_0\displaystyle\frac{ S}{ d}$[F]
固体誘電体を挿入した後の静電容量を $C_1$[F]は、
$C_1=\displaystyle\frac{ σS}{ V_0}=\displaystyle\frac{ ε_0}{ \displaystyle\frac{ 3}{ 4 }+\displaystyle\frac{ ε_0}{ 4ε_1 }}\displaystyle\frac{ S}{ d}$[F]
$ε_1>ε_0 $なので、$C_1>C_2$ となりますので、(3)は正しい記述です。
固体誘電体を導体に変えた場合の位置Pの電位を $V_{P2}$[V]とすれば、$ε_1 $が∞になることなので、
$V_{P1}=\displaystyle\frac{ 2+\displaystyle\frac{ ε_0}{ ε_1 }}{ 3+\displaystyle\frac{ ε_0}{ ε_1 }} V_0$[V]
$V_{P2}=\displaystyle\frac{ 2}{ 3} V_0$[V]
$V_{P0}=\displaystyle\frac{ 3}{ 4}V_0$[V]なので、$V_{P2}<V_{P0}$ となりますので、(4)の記述は誤りです。
固体誘電体を導体に変えた場合の静電容量を $C_2$[C]とすれば、$ε_1 $が∞になることなので、
$C_1=\displaystyle\frac{ ε_0}{ \displaystyle\frac{ 3}{ 4 }+\displaystyle\frac{ ε_0}{ 4ε_1 }}\displaystyle\frac{ S}{ d}$[F]
$C_2=\displaystyle\frac{ ε_0}{ \displaystyle\frac{ 3}{ 4 }}\displaystyle\frac{ S}{ d}=\displaystyle\frac{ 4}{ 3 } ε_0\displaystyle\frac{ S}{ d}$[F]
$C_0=ε_0\displaystyle\frac{ S}{ d}$[F]なので、$C_2>C_0$ となりますので、(5)は正しい記述です。
答え (4)
2014年(平成26年)問1【電験理論の過去問題】
極板A-B間が比誘電率 $εr=2$ の誘電体で満たされた平行平板コンデンサがある。極板間の距離は $d$[m]、極板間の直流電圧は $V_0 $[V]である。極板と同じ形状と大きさをもち、厚さが $\displaystyle\frac{ d}{ 4 } $[m]の帯電していない導体を図に示す位置P-Q間に極板と平行に挿入したとき、導体の電位の値[V]として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、コンデンサの端効果は無視できるものとする。
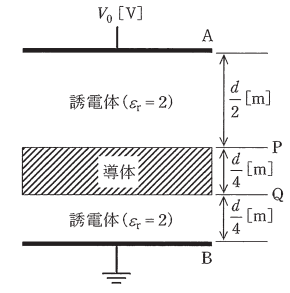
(1) $\displaystyle\frac{ V_0}{ 8 }$ (2) $\displaystyle\frac{ V_0}{ 6 }$ (3) $\displaystyle\frac{ V_0}{ 4 }$ (4) $\displaystyle\frac{ V_0}{ 3 }$ (5) $\displaystyle\frac{ V_0}{ 2 }$
AP間の静電容量を $C_{AP}$[F]、QB間の静電容量 $C_{QB}$[F]とすると。
$C_{AP}=\displaystyle\frac{ εrε_0S}{ \displaystyle\frac{ d}{ 2 } }=\displaystyle\frac{ 4ε_0S}{ d }$[F]
$C_{QB}=\displaystyle\frac{ εrε_0S}{ \displaystyle\frac{ d}{ 4 } }=\displaystyle\frac{ 8ε_0S}{ d }$[F]
コンデンサの電荷は $Q$[C]は、$ Q=CV$ で表されます。$C_{AP}$ と、$C_{QB}$ に蓄えられる電荷量は等しくなりますので、
$ Q=C_{AP}(V_0-V)=C_{QB}V$
$ \displaystyle\frac{ 4ε_0S}{ d }(V_0-V)=\displaystyle\frac{ 8ε_0S}{ d }V$
$ V=\displaystyle\frac{ V_0}{ 3 }$
答え (4)
電験三種の理論科目に出題される「静電気分野」のページ
1.クーロンの法則とは
2.電界とガウスの法則
3.静電界中の電位と電圧
4.静電誘導と誘電分極
5.平行平板コンデンサの静電容量
6.コンデンサの直列接続と並列接続
7.静電エネルギー
8.誘電体とコンデンサ
9.導体球と同心球導体の静電容量






