第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「コンデンサの直列接続と並列接続」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「コンデンサの直列接続と並列接続」の過去問題も解説しています。
コンデンサの並列接続
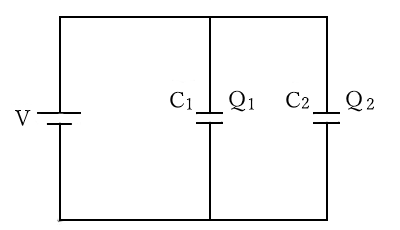
静電容量が $C_1$[F]と $C_2$[F]のコンデンサを並列に接続した回路に、電圧 $V$[V]の電池を取り付けます。
2つのコンデンサに蓄えられる電荷量をそれぞれ、$Q_1$[C]と$Q_2$[C]とすると、2つのコンデンサに蓄えることができる電荷量の合計 $Q$[C]は、次のようになります。
$Q=Q_{ 1 }+ Q_{ 2 }=C_{ 1 }V+C_{ 2 }V=(C_{ 1 }+C_{ 2 })V$
コンデンサを並列接続した場合の合成静電容量 $C$[F]は、
$C=C_{ 1 }+C_{ 2 }$
となります。この式はコンデンサが複数あるときでも成立します。
コンデンサ並列回路の公式
各電荷:$Q_1=C_{ 1 }V$,$Q_2=C_2V$
全電荷:$Q=Q_1+ Q_2$
合成静電容量:$C=C_1+C_2$

コンデンサの直列接続
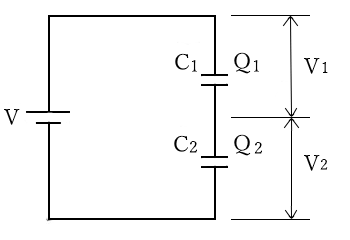
静電容量が $C_1$[F]と $C_2$[F]のコンデンサを直列に接続した回路に、電圧 $V$[V]の電池を取り付けます。
電池をつなぐ前に2つのコンデンサには電荷は蓄えられていなかったとすると、2つのコンデンサの電荷量、$Q_1$[C]と $Q_2$[C]は同量の電荷を蓄えます( $Q=Q_1=Q_2$ )。
コンデンサの両端にかかる電圧をそれぞれ、$V_1$[V]と $V_2$[V]とすると、次の関係が成り立ちます。
$Q=C_{ 1 }V_{ 1 }$
$Q=C_{ 2}V_{ 2 }$
一方、$V=V_{ 1}+V_{ 2 }$[V]の関係がありますので、
$V=V_{ 1}+V_{ 2 }=\displaystyle\frac{Q}{C_{ 1 }}+\displaystyle\frac{Q}{C_{ 2 }}=\biggl(\displaystyle\frac{1}{C_{ 1 }}+\displaystyle\frac{1}{C_{ 2 }}\biggl)Q$
コンデンサを直列接続した場合の合成静電容量の関係式は、
$C=\displaystyle\frac{1}{\displaystyle\frac{1}{C_{ 1 }}+\displaystyle\frac{1}{C_{ 2 }}}=\displaystyle\frac{C_1C_2}{C_1+C_2}$
となります。この式はコンデンサが複数あるときでも成立します。
コンデンサ直列回路の公式
各電荷:$Q_1=C_1V_1$,$Q_2=C_2V_2$
全電荷:$Q=Q_1=Q_2$
合成静電容量:$C=\displaystyle\frac{1}{\displaystyle\frac{1}{C_{ 1 }}+\displaystyle\frac{1}{C_{ 2 }}}=\displaystyle\frac{C_1C_2}{C_1+C_2}$
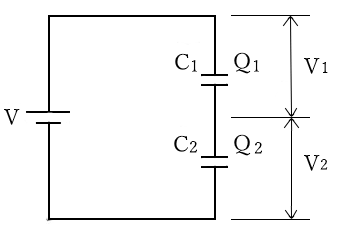
全電圧:$V=V_1+V_2$
各電圧:$V_1=\displaystyle\frac{Q_1}{C_1}$ ,$V_2=\displaystyle\frac{Q_2}{C_2}$
分担電圧:$V_1=\displaystyle\frac{C_2}{C_1+C_2}×V$ ,$V_2=\displaystyle\frac{C_1}{C_1+C_2}×V$
電験三種-理論の過去問解説:コンデンサの直列接続と並列接続
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1997年(平成9年)問1【電験理論の過去問題】
静電容量がそれぞれ C1[F],C2[F]及び C3[F]の3個のコンデンサを図のように接続し、直流電圧 V[V]を加えたとき、コンデンサ C2 に蓄えられる電荷の値[C]として、正しいものは次のうちどれか。
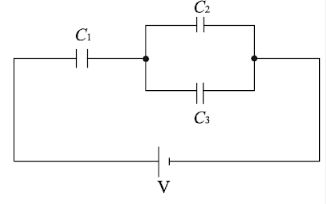
並列接続部分の合成静電容量 Cp[F]とすると、
$C_p=C_{ 2 }+C_{ 3 }$[F]
コンデンサを直列接続したときの電荷量 Q[C]は、
$Q=C_{ 1 }V_{ 1 }=C_{ p}V_{ 2 }$
$C_{ 1 }V_{ 1 }=(C_{ 2 }+C_{ 3 })V_{ 2 }$
$V_{ 1 }=\displaystyle\frac{(C_{ 2 }+C_{ 3 })V_{ 2 }}{C_{ 1}}$
V=V1+V2[V]の関係がありますので、
$V=\displaystyle\frac{(C_{ 2 }+C_{ 3 })V_{ 2 }}{C_{ 1}}+V_{ 2 }=\displaystyle\frac{(C_{ 1}+C_{ 2 }+C_{ 3 })V_{ 2 }}{C_{ 1}}$
$V_{ 2 }=\displaystyle\frac{C_{ 1}V}{C_{ 1}+C_{ 2 }+C_{ 3 }}$
コンデンサ C2 に蓄えられる電荷の値 Q[C]は、
$Q=C_{ 2}V_{ 2 }=\displaystyle\frac{C_{ 1}C_{ 2}V}{C_{ 1}+C_{ 2 }+C_{ 3 }}$[C]
答え (4)
1999年(平成11年)問12【電験理論の過去問題】
図の回路において、スイッチSを開いた状態では端子a,b間の電圧は 15[V]であった。スイッチSを閉じた状態における端子a,b間の電圧[V]の値として、正しいのは次のうちどれか。ただし、C1=0.6[μF],C2=1[μF],C0=0.3[μF]とする。また、スイッチSを閉じる前の C0 の電荷は零とする。
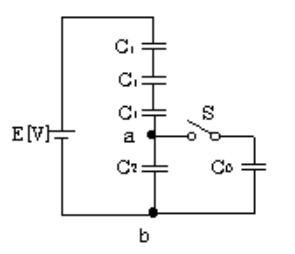
(1) 8 (2) 9 (3) 10 (4) 11 (5) 12
スイッチSが開いている場合、コンデンサは直列接続なので、各コンデンサは、同量の電荷を蓄えます。各コンデンサに蓄えれれる電荷量を Q[C]、ab間の電圧を V2[V]とすると、
$Q=C_2V_2=1×10^{-6}×15=15$ [μC]
したがって E[V]は、
$E=\displaystyle\frac {Q}{C_1}×3+ \displaystyle\frac {Q}{C_2} =\displaystyle\frac {15}{0.6}×3+ \displaystyle\frac {15}{1} =90$ [V]
スイッチSが閉じている場合 、$ \displaystyle\frac { C_1 }{3} $のコンデンサと、$C_2$ と $C_3$ が並列に接続された 1.3 [μF] のコンデンサが直列に接続された回路になりますので、1.3 [μF] に加わる電圧は、容量に反比例しますので、
$E_{ab}=90× \displaystyle\frac {0.2}{1.3+0.2}=12$[V]
答え (5)
2001年(平成13年)問8【電験理論の過去問題】
静電容量がそれぞれ 20[μF]及び 30[μF]の二つのコンデンサを図1のように直列に接続し、10[V]の直流電流を加えて充電した。その後、これらのコンデンサを直流電源から切り離して、同じ極性の端子同士を図2のように接続した。このとき、二つのコンデンサの端子電圧 E[V]の値として、正しいのは次のうちどれか。
ただし、二つのコンデンサの初期電荷は零とする。
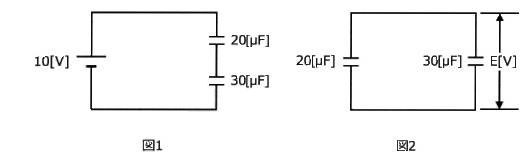
(1) 2.4 (2) 3.6 (3) 4.8 (4) 6.0 (5) 7.2
図1の合成静電容量を C1[μF]とすると、
$\displaystyle\frac{1}{C_{ 1}}=\displaystyle\frac{1}{20}+\displaystyle\frac{1}{30}=\displaystyle\frac{1}{12}$
$C_{ 1}=12$[μF]
図1で2つのコンデンサは直列接続のため、同量の電荷量を蓄えます。蓄えられる電荷を Q[C]とすると
$Q=CV=12×10=120$[μC]
図2で充電されたコンデンサを並列に接続するので、全電荷量は 2Q=240[μC]になります。
また、図2の合成静電容量を C2[μF]とすると
$C_{ 2}=20+30=50$[μF]
よって
$240=50×V$
$V=4.8$[V]
答え (3)
2003年(平成15年)問1【電験理論の過去問題】
図のように、静電容量 C1,C2 及び C3 のコンデンサが接続されている回路がある。スイッチSが開いているとき、各コンデンサの電荷は、すべて零であった。スイッチSを閉じると、C1=5[μF]のコンデンサには 3.5×10-4[C]の電荷が、C2=2.5[μF]のコンデンサには 0.5×10-4[C]の電荷が充電された。静電容量 C3[μF]の値として、正しいのは次のうちどれか。
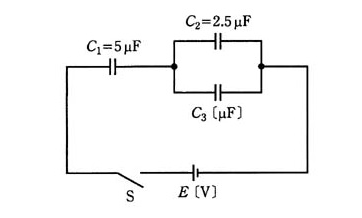
(1) 0.2 (2) 2.5 (3) 5 (4) 7.5 (5) 15
C2 と C3 の合成静電容量を C23 とすると
$C_{ 23}=C_{ 2}+C_{ 3}$
C1 の電荷量 Q1[C]と C23 の電荷量 Q23[C]は等しいので
$Q_{ 3}=Q_{ 1}-Q_{ 2}=3×10^{-4}$[C]
C2 と C3 にかかる電圧 V[V]は
$V=\displaystyle\frac{Q_{ 2}}{C_{ 2}}=\displaystyle\frac{Q_{ 3}}{C_{ 3}}$
よって
$\begin{eqnarray}C_{ 3}&=&\displaystyle\frac{Q_{ 3}}{Q_{ 2}}×C_{ 2}\\\\&=&\displaystyle\frac{3×10^{ -4}}{0.5×10^{ -4}}×2.5×10^{ -6}\\\\&=&15×10^{ -6}[F]\end{eqnarray}$
答え (5)
2008年(平成20年)問5【電験理論の過去問題】
図1に示すように、二つのコンデンサ C1=4[μF]と C2=2[μF]が直列に接続され、直流電圧 6[V]で充電されている。次に電荷が蓄積されたこの二つのコンデンサを直流電源から切り離し、電荷を保持したまま同じ極性の端子同士を図2に示すように並列に接続する。並列に接続後のコンデンサの端子間電圧の大きさ V[V]の値として、正しいのは次のうちどれか。
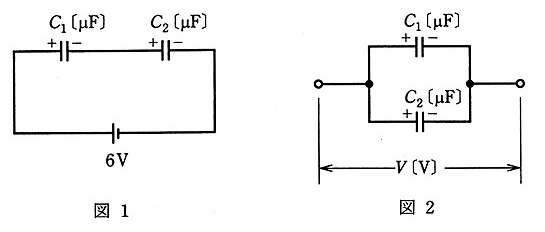
(1) $\displaystyle\frac{2}{3}$ (2) $\displaystyle\frac{4}{3}$ (3) $\displaystyle\frac{8}{3}$ (4) $\displaystyle\frac{16}{3}$ (5) $\displaystyle\frac{32}{3}$
図1の二つのコンデンサの合成静電容量をコンデンサ CS とすると、
$\displaystyle\frac{1}{C_{ S}}=\displaystyle\frac{1}{4}+\displaystyle\frac{1}{2}=\displaystyle\frac{3}{4}$
$C_{ S}=\displaystyle\frac{4}{3}$[μF]
CS に蓄えられる電荷量 QS は
$Q_{S}=C_{ S }V=\displaystyle\frac{4}{3}×10^{ -6 }×6=8×10^{ -6 }$[C]
図2の二つのコンデンサの合成静電容量をコンデンサ CP とすると、
$C_{ P}=4+2=6$[μF]
このとき C1 と C2 のコンデンサは 8×10-6[C]の電荷量を持っているので
$V=\displaystyle\frac{8×2×10^{ -6 }}{6×10^{ -6 }}=\frac{8}{3 }$[V]
答え (3)
2012年(平成24年)問1【電験理論の過去問題】
図1及び図2のように、静電容量がそれぞれ 4 [μF] と 2 [μF] のコンデンサ C1 及び C2、スイッチ S1 及びS2 からなる回路がある。コンデンサ C1 と C2 には、それぞれ 2 [μC] と 4 [μC] の電荷が図のような極性で蓄えられている。この状態から両図ともスイッチ S1 及び S2 を閉じたとき、図1のコンデンサ C1 の端子電圧を V1 [V] 、図2のコンデンサ C2 の端子電圧を V2 [V] とすると、電圧比 $\displaystyle\left|\frac{V_{ 1}}{V_{ 2}}\right| $の値として、正しいものを次の(1)~(5)のうちから一つ選べ。
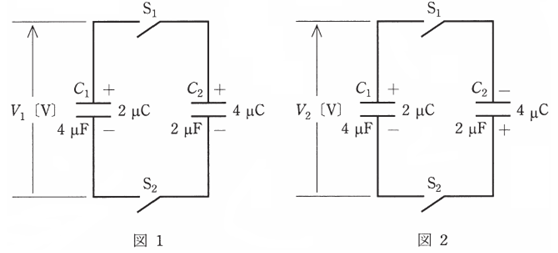
(1) $\displaystyle\frac{1}{3}$ (2) 1 (3) 3 (4) 6 (5) 9
図1の2つのコンデンサの合成静電容量を Ca、電荷量を Qa とすると、
$C_a=C_{ 1}+C_{ 2}=4+2=6$[μF]
$Q_a=Q_{ 1}+Q_{ 2}=2+4=6$[μC]
よって図1の端子電圧 V1[V]は
$V_{ 1}=\displaystyle\frac{Qa}{Ca }=\frac{6×10^{ -6 }}{6×10^{ -6 }}=1$[V]
図2の2つのコンデンサの合成静電容量を Cb、電荷量を Qb とすると、
$C_b=C_{ 1}+C_{ 2}=4+2=6$[μF]
$Q_b=Q_{ 1}+Q_{ 2}=2-4=-2$[μC]
蓄えられている電荷の向きに注意が必要です。Q2 の向きは端子電圧 V2 と逆向きです。
よって図2の端子電圧 V2[V]は
$V_{ 2}=\displaystyle\frac{Qb}{Cb }=\frac{-2×10^{ -6 }}{6×10^{ -6 }}=-\frac{1}{3}$[V]
$\displaystyle\left|\frac{V_{ 1}}{V_{ 2}}\right| =\displaystyle\left|\frac{1}{-\frac{1}{3}}\right|=3$
答え (3)
2012年(平成24年)問15【電験理論の過去問題】
図のように、三つの平行平板コンデンサを直並列に接続した回路がある。ここで、それぞれのコンデンサの極板の形状及び面積は同じであり、極板間には同一の誘電体が満たされている。なお、コンデンサの初期電荷は零とし、端効果は無視できるものとする。いま、端子a-b間に直流電圧 300[V]を加えた。
このとき、次の(a)及び(b)の問に答えよ。
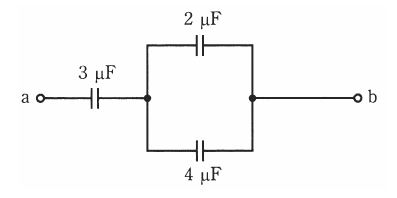
(a) 静電容量が 4[μF]のコンデンサに蓄えられる電荷 Q[C]の値として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1) 1.2×10-4 (2) 2×10-4 (3) 2.4×10-4 (4) 3×10-4 (5) 4×10-4
(b) 静電容量が 3 [μF] のコンデンサの極板間の電界の強さは、4 [μF] のコンデンサの極板間の電界の強さの何倍か。倍率として、正しいものを次の(1)~(5)のうちから一つ選べ。
(1) $\displaystyle\frac{3}{4}$ (2) 1.0 (3) $\displaystyle\frac{4}{3}$ (4) $\displaystyle\frac{3}{2}$ (5) 2.0
(a) 並列部分のコンデンサの合成静電容量は、6 [μF] になります。静電容量が 3[μF]のコンデンサに印加される電圧を V1[V]、並列部分の電圧を V2[V]とすると、
$Q=C_{ 1 }V_{ 1 }=3×10^{-6}V_{ 1 }$
$Q=C_{ 2}V_{ 2 }=6×10^{-6}V_{ 2 }$
$V_{ 1 }=2V_{ 1 }$ … (1)
一方、$V=V_{ 1}+V_{ 2 }$ の関係がありますので、
$300=V_{ 1}+V_{ 2 }$ … (2)
(1),(2)式より、
$V_{ 1 }=200$[V]
$V_{ 2 }=100$[V]
静電容量が 4[μF]のコンデンサに蓄えられる電荷 Q[C]は、
$Q=CV_{ 2 }=4×10^{-6}×100=4×10^{-4}$[C]
答え (5)
(b) 電圧と電界の関係式は、
$V=Ed$[V]…(3)
平行板コンデンサの静電容量 C[F]は、
$C=\displaystyle\frac{ ε S}{ d }$[F]…(4)
(3),(4)式より、
$E=\displaystyle\frac{ V}{ d }=\displaystyle\frac{ V}{ \displaystyle\frac{ ε S}{ C } }=\displaystyle\frac{ CV}{ ε S }$
静電容量が 3 [μF] のコンデンサの極板間の電界の強さ E1 は、
$E_1=\displaystyle\frac{ CV}{ ε S }=\displaystyle\frac{ 3×200}{ ε S }$
静電容量が 4 [μF] のコンデンサの極板間の電界の強さ E2 は、
$E_2=\displaystyle\frac{ CV}{ ε S }=\displaystyle\frac{ 4×100}{ ε S }$
それぞれのコンデンサの極板の形状及び面積は同じであり、極板間には同一の誘電体が満たされているので、
$\displaystyle\frac{E_1}{E_2}=\displaystyle\frac{600}{400}=\displaystyle\frac{3}{2}$
答え (4)
2014年(平成26年)問5【電験理論の過去問題】
図のように、コンデンサ3個を充電する回路がある。スイッチS1及びS2を同時に閉じてから十分に時間が経過し、定常状態となったとき、a点からみたb点の電圧の値 [V] として、正しいものを次の(1)~(5)のうちから一つ選べ。ただし、各コンデンサの初期電荷は零とする。
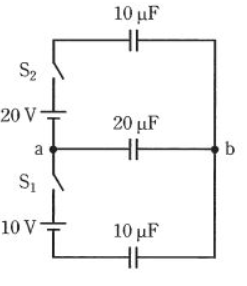
重ね合わせの理で解きます。コンデンサの直列接続時の分圧は、抵抗の並列接続の電流分配に同じで逆比になります。
20V の電源を残したとき
$V_2=20×\displaystyle\frac{ 10 }{ 10+(20+10) }=5$ [V]
a点から見たb点の電位は +5 [V]
10V の電源を残したとき
$V_1=10 ×\displaystyle\frac { 10 }{ 10+(20+10) }=2.5$ [V]
a点から見たb点の電位は-2.5 [V]
それぞれの回路を重ね合わせてa点から見たb点の電位は、
5 [V] -2.5 [V] =2.5 [V]
答え (3)
2015年(平成27年)問9【電験理論の過去問題】
図のように、静電容量 $C_1=10$μF、$C_2=900$μF、$C_3=100$μF、$C_4=900$μF のコンデンサからなる直並列回路がある。この回路に周波数 $f=50$Hz の交流電圧 $V_{in}$[V]を加えたところ、$C_4$ の両端の交流電圧は $V_{out}$[V]であった。このとき、$\displaystyle \frac{V_{out}}{V_{in}}$ の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
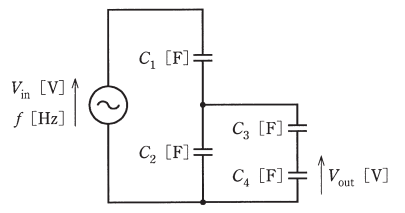
$C_2$、$C_3$、$C_4$ のコンデンサの合成静電容量を $C_{234}$ とすると、
$\begin{eqnarray}C_{234}&=&C_2+\displaystyle \frac{C_3C_4}{C_3+C_4}\\\\&=&900+\displaystyle \frac{100×900}{100+900}=990μF\end{eqnarray}$
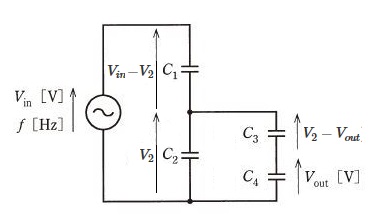
コンデンサ $C_2$ の両端の電圧を $V_2$[V]とすると、
$C_1(V_{in}-V_2)=C_{234}V_2$
$10(V_{in}-V_2)=990V_2$
$V_2=\displaystyle \frac{V_{in}}{100}$
$C_3(V_2-V_{out})=C_4V_{out}$
$100(V_2-V_{out})=900V_{out}$
$100(\displaystyle \frac{V_{in}}{100}-V_{out})=900V_{out}$
$V_{in}=1000V_{out}$
答え (1)
2015年(平成27年)問16【電験理論の過去問題】
図1の端子a-d間の合成静電容量について、次の(a)及び(b)の問に答えよ。
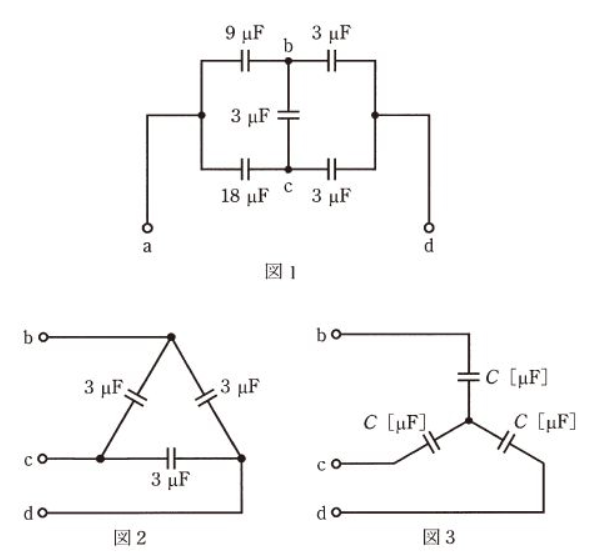
(a) 端子b-c-d間は図2のようにΔ結線で接続されている。これを図3のようにY結線に変換したとき、電気的に等価となるコンデンサ C の値 [μF] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 1.0 (2) 2.0 (3) 4.5 (4) 6.0 (5) 9.0
(b) 図3を用いて、図1の端子b-c-d間をY結線回路に変換したとき、図1の端子a-d間の合成静電容量 C0 の値 [μF] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 3.0 (2) 4.5 (3) 4.8 (4) 6.0 (5) 9.0
(a) スターデルタ変換で解きます。図1を変換すると、次の図のようになります。
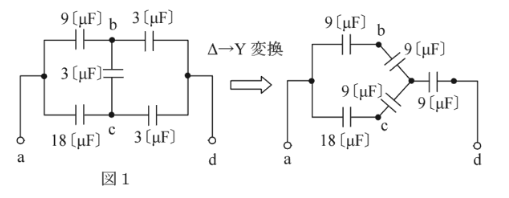
$3×3=9.0$ [μF]
答え (5)
(b) 並列部分の合成静電容量 $C_p$ は、
$C_p=\displaystyle\frac{9×9}{9+9}+\displaystyle\frac{18×9}{18+9}=10.5$ [μF]
合成静電容量 $C_o$ は、
$C_o= \displaystyle\frac {10.5×9}{10.5+9}≒4.8$ [μF]
答え (3)
2016年(平成28年)問7【電験理論の過去問題】
静電容量が1μFのコンデンサ3個を下図のように接続した回路を考える。全てのコンデンサの電圧を 500V以下にするために、a-b間に加えることができる最大の電圧 Vm の値 [V] として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、各コンデンサの初期電荷は零とする。
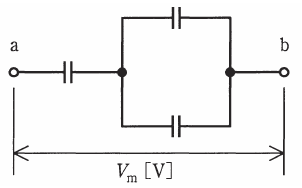
(1) 500 (2) 625 (3) 750 (4) 875 (5) 1000
並列部分を合成します。
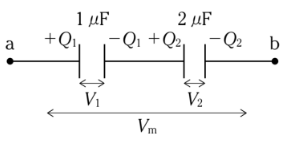
直列に並んだ2つのコンデンサに蓄えられる電荷 $Q_1$ と $Q_2$ は等しいので、
$C_1V_1=C_2V_2$
$V_1=2V_2$
a-b間に加えることができる最大の電圧 Vm の値は、
$V_m=V_1+V_2=500+250=750$ [V]
答え (3)
電験三種の理論科目に出題される「静電気分野」のページ
1.クーロンの法則とは
2.電界とガウスの法則
3.静電界中の電位と電圧
4.静電誘導と誘電分極
5.平行平板コンデンサの静電容量
6.コンデンサの直列接続と並列接続
7.静電エネルギー
8.誘電体とコンデンサ
9.導体球と同心球導体の静電容量






