電験3種の数学を学ぶ前に、中学校で習う関数について勉強をしましょう。「関数」と聞くと何やら難しそうなイメージがありますが、関数とはその名のとおり「数の関係」を表すものです。簡単な説明になりますが、方程式は x の未知数を求めるもので、関数は y と x の「関係性」を求めるものです。どのような「関係性」があるのかについて、基礎からおさらいをしていきましょう。
関数を理解するのに必要な用語について
1.関数
2つの変数x、yがあり、xの値に対応してyの値が決まるとき、yはxの関数といいます。
2.数直線
直線上に数を対応させるとき,この直線を数直線といいます。数直線上では、数の大小関係を確認できます。
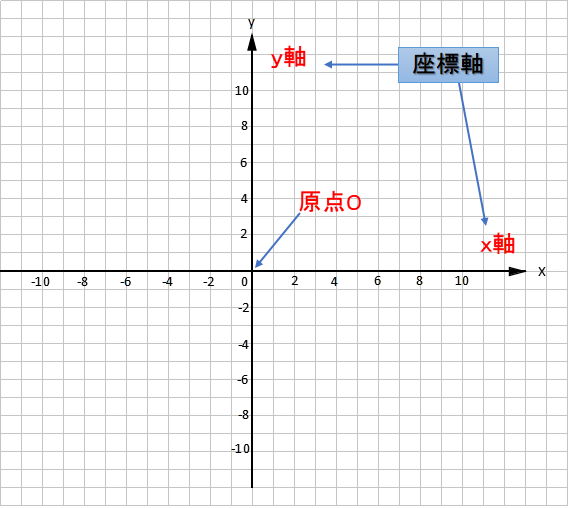
3.座標軸
2本の数直線を直角に交わるようにし、その交点をOとします。このとき、横向きの直線を「x軸」、縦向きの直線を「y軸」と表し、x軸とy軸をあわせて座標軸とよびます。また点Oのことを原点と呼びます。
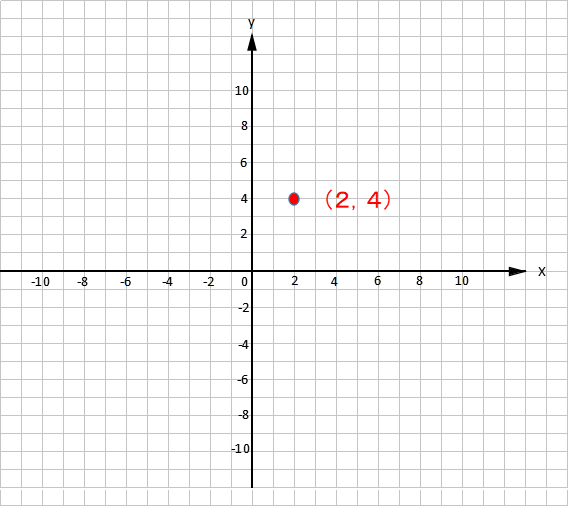
4.座標
点の位置を表すのに使う数の組です。下の図のように点の位置の座標は(2,4)と表します。また(2,4)の
「2をx座標」
「4をy座標」
といいます。
比例と反比例
一方の値が2倍、3倍…になると、もう一方の値も2倍、3倍…となるような関係のことを比例の関係と言います。
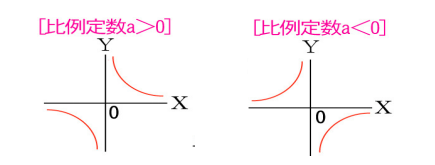
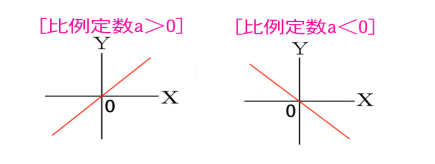
比例の関係は、$ y=ax$ と式で表すことができます。この $ a (a≠0)$ は比例定数といいます。比例関係をグラフで表すと、下図のような原点を通る直線になります。
一方の値が2倍、3倍…になると、もう一方の値も1/2倍、1/3倍…となるような関係のことを反比例の関係と言います。
反比例の関係は、$ y=\displaystyle \frac{a}{x}$ と式で表すことができます。この $ a (a≠0)$ は比例定数といいます。反比例の関係をグラフで表すと、下図のような双曲線になります。
比例と反比例の概念
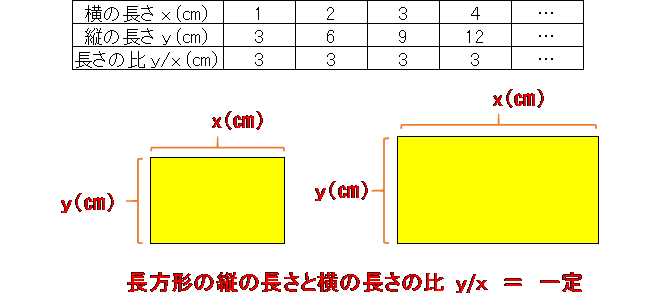
次の表は縦横の長さの比が一定の長方形の横の長さ x(㎝) と縦の長さ y(㎝) の関係をあらわしています。変化する2つの量の比が常に一定の数になる場合を比例といいます。その「一定の数」が比例定数になるので,「一定の数」を見つけることが比例を考えるポイントになります。
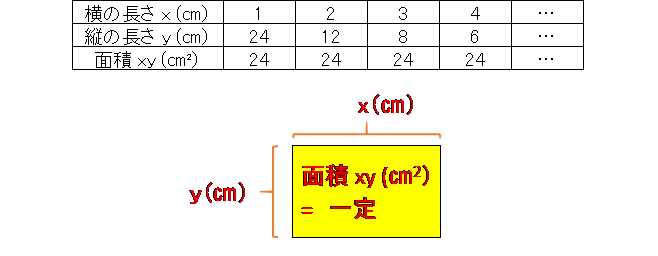
次の表は面積が一定の長方形の横の長さ x(㎝) と縦の長さ y(㎝) の関係をあらわしています。変化する2つの量の積が常に一定の数になる場合を反比例といいます。その「一定の数」が比例定数になるので,「一定の数」を見つけることが反比例を考えるポイントになります。
比例定数の求め方
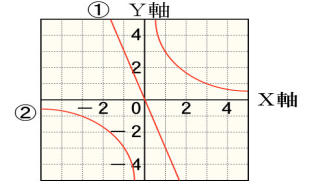
①、②それぞれのグラフについて、yをxの式で表してみます。
①のグラフは比例のグラフなので、$ y=ax$ ・・・ ①とします。
グラフは点(-1,3)を通るので、$ x=-1,y=3$ を①式に代入します。
$ 3=-1×a$ ⇒ $ a=-3$
よって①のグラフは $ y=-3x$ となります。
②のグラフは反比例のグラフなので、$ y=\displaystyle \frac{a}{x}$ ・・・ ②とします。グラフは点(1,3)を通るので、$ x=1,y=3$ を②式に代入します。
$ 3=\displaystyle \frac{a}{1}$ ⇒ $ a=3$
よって②のグラフは $ y=\displaystyle \frac{3}{x}$ となります。
演習問題1
次の問題が解けますか?
a y が x に比例し x=2 のとき y=-4 となりました。
① y を x の式で表してください。
② x=5 の時の y の値はいくつですか?
b y は x に反比例し、x=2 のとき y=-4 となりました。
① y を x の式で表してください。
② x=2 のときの y の値はいくつですか?
演習問題1の解答
aの解答 y が x に比例し x=2 のとき y=-4 となりました。
① y を x の式で表してください。
$ y=ax$
$ -4=2a$
$ a=-2$
$ y=-2x$ (答え)
② x=5 の時の y の値はいくつですか?
$ y=-2x$ に $ x=5$ を代入します。
$ y=-2×5=-10$ (答え)
bの解答 y は x に反比例し、x=2 のとき y=-4 となりました。
① y を x の式で表してください。
$ y=\displaystyle \frac{a}{x}$
$ -4=\displaystyle \frac{a}{2}$
$ a=-8$
$ y=\displaystyle \frac{-8}{x}$ (答え)
② x=2 のときの y の値はいくつですか?
$ y=\displaystyle \frac{-8}{x}$ に $ x=2$ を代入します。
$ y=\displaystyle \frac{-8}{2}=-4$ (答え)
一次関数
一次関数とは$ y=ax+b$ で表される式のことです。一般的に1次関数の式は0でない定数aと定数bを用いて表します。
xの係数aは「傾き」、定数項bは「切片」といいます。一次関数のグラフは、y軸上に切片があり、そこから変化の割合(傾き)分進みます。
$ 変化の割合=\displaystyle \frac{yの増加量}{xの増加量}$
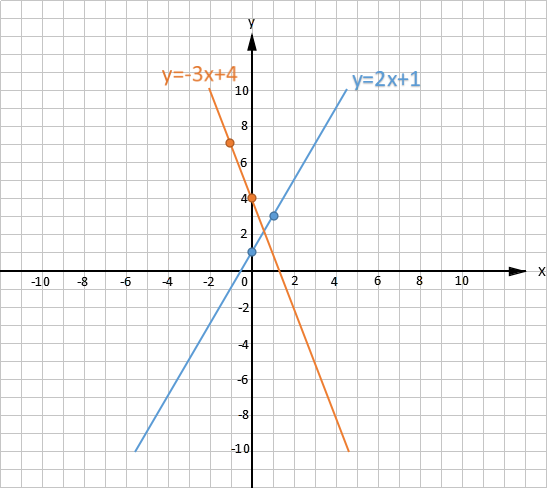
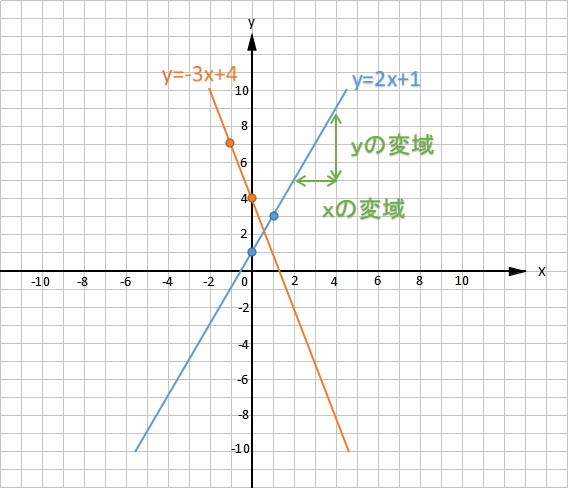
下の図は$ y=2x+1$ と $ y=-3x+4$ のグラフです。$ y=2x+1$ のグラフは、y軸上に切片の1があります。x=0,y=1 と x=1,y=3 を通りますので、変化の割合は、
$ 変化の割合=\displaystyle \frac{3-1}{1-0}=2=$傾き
となります。
$ y=-3x+4$ のグラフは、y軸上に切片の4があります。x=0,y=4 と x=-1,y=7 を通りますので、変化の割合は、
$ 変化の割合=\displaystyle \frac{7-4}{-1-0}=-3=$傾き
となります。
変域は、グラフの範囲のことです。グラフを描いたときの横の範囲がxの変域、縦の範囲がyの変域となります。
例えば、$ y=2x+1$ のグラフでxの変域を2≦x≦4とすれば、yの変域は5≦y≦9 となります。
演習問題2
次の問題が解けますか?
a $ 6x-3y+18=0$の変化の割合はいくつですが?
b xの増加量が3で、yの増加量が9のときの変化の割合はいくつですか?
c 点 (1,−3)から点(6,10)に変化したときの変化の割合はいくつですか?
d y=2x-9でxが-1から4まで変化するときのyの増加量はいくつですか?
e y=4x-5でxの増加量が3のときのyの増加量はいくつですか?
演習問題2の解答
aの解答
$ 6x-3y+18=0$の変化の割合はいくつですが?
$ 6x-3y+18=0$
$ 3y=6x+18$
$ y=2x+6$
変化の割合は2
bの解答
xの増加量が3で、yの増加量が9のときの変化の割合はいくつですか?
$ 変化の割合=\displaystyle \frac{yの増加量}{xの増加量}$
$ 変化の割合=\displaystyle \frac{9}{3}=3$
cの解答
点 (1,−3)から点(6,10)に変化したときの変化の割合はいくつですか?
$ 変化の割合=\displaystyle \frac{10-(-3)}{6-1}=\frac{13}{5}$
dの解答
y=2x-9でxが-1から4まで変化するときのyの増加量はいくつですか?
$ 変化の割合=\displaystyle \frac{yの増加量}{xの増加量}$
$ 2=\displaystyle \frac{yの増加量}{4-(-1)}$
$ yの増加量=10$
eの解答
y=4x-5でxの増加量が3のときのyの増加量はいくつですか?
$ 4=\displaystyle \frac{yの増加量}{3}$
$ yの増加量=12$
以上が電気数学を学ぶ前に必要な中学校で習う関数についてのおさらいです。変化の割合についてよく理解をしておいてください。電験3種の問題を解くにあたって、この考え方が非常に役に立ちます。