第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「静電界中の電位と電圧」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「静電界中の電位と電圧」の過去問題も解説しています。
電位とは?
高いところにある物体は落とすことによって下にある物体に対して仕事ができます。高いところにある物体はエネルギーを持っているといえます。このエネルギーのことを重力による位置エネルギーといいます。
また物体を高い位置に運ぶには仕事をしなければいけません。その仕事をするのにエネルギーが必要です。物体を運ぶ位置が高い・低いによって、必要なエネルギーの大きさが違ってきます。
電気の世界でも、高い・低いによって電荷の持つエネルギーが変わってきます。このように電気的な位置のことを「電位」といい単位は $V$(ボルト)を使います。電位とは電界中における位置エネルギーの大小という具合に考えておいて下さい。
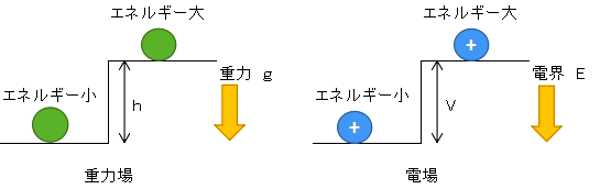
一様な電界による電圧
電界は大きさと向きを持つベクトルで表され、その強さは $E$[V/m]で表します。$E$[V/m]の電界中では、$q$[C]の電荷は $qE$[N]の力を受けます。
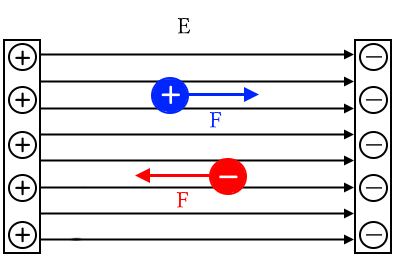
電界 $E$[V/m]中に置かれた電荷 $q$[C]に働く力 $F$[N]
$F=qE$[N]
正の電荷は電界と同じ向き、負の電荷は電界と逆向きに力を受けます。
この静電気力によって、電荷 $q$[C]が移動するとき、電界 $E$[V/m]が電荷 $q$[C]にする仕事 $W$[J]を考えてみます。(仕事)=(力の大きさ)×(移動距離)と定義されていますので、移動距離を $d$[m]とすると、
$W=Fd=qEd=q(Ed)$[J]
となります。電界 $E$[V/m]はどこでも同じ「一様」ですので、移動距離 $d$[m]が決まれば、電荷 $q$[C]のする仕事 $W$[J]は電荷のもつ電気量 $q$[C]に比例します。このときA点からB点に移動したとすれば、A点とB点が持つ位置エネルギー(電位)の差を「電位差」または「電圧」と定義し、$V$[V]で表します。
一様な電界 $E$ による電位差 $V$ の定義式
$V=Ed$[V]
$V$[V]:電位差
$E$[V/m]:電界の強さ
$d$[m]:長さ
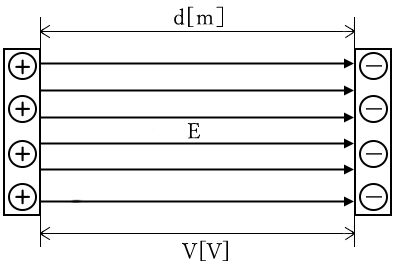
電圧 $V$ と仕事 $W$ の関係
$W=qV$[J]
$W$[J]:仕事量
$q$[C]:電荷
$V$[V]:電位差
電荷が2点間を移動するとき、2点間の電位差が大きいほど、大きな仕事を取り出すことができます。また、一様な電界中では、どこでも電界の向きと大きさが同じなので、電荷が電界から得る仕事は、途中の経路とは無関係です。電圧は仕事と同じようにスカラー量となります。
点電荷が作る電界による電位
点電荷がつくる電位は、正の点電荷の近くほど大きく、負の点電荷に近いほど小さくなります。電気量 $Q$[C]の点電荷から距離 $r$[m]の位置の電位 $V$[V]は、$Q$[C]から無限に離れた点を電位の基準「ゼロ」として求めます。
この考え方から求めるには、積分の知識が必要ですので、点電荷が作る電位は「公式」として覚えてしまいましょう。
点電荷が作る電位 $V$ を求める公式
$ V=\displaystyle \frac{ Q }{ 4πε_{ 0 } r }$[V]
$V$[V]:電位
$ε_0$:真空の誘電率
$Q$[C]:電荷
$r $[m]:電荷からの距離
複数の点電荷がある場合の電位は、それぞれの点電荷の電位を足し合わせます。電位は高いか低いかのみですので、向きのないスカラー量です。
等電位面
電位の等しい点を結んでできた曲面を等電位面といいます。地図で高さを表した等高線のようなイメージです。たとえば点電荷から距離 r[m]の位置は電位が等しくなりますので、球状の等電位面ができます。また、一様な電界中では、電界を作っている電極と平行な等電位面ができます。
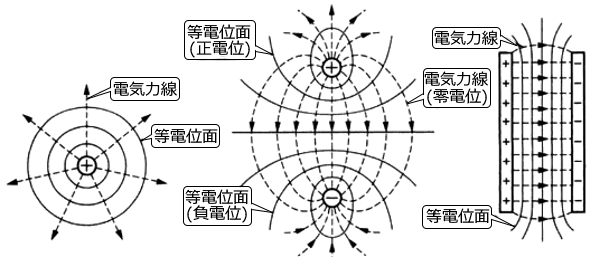
- 等電位面上では電荷を動かしても電界は仕事をしません。
等電位面上では、電位差が 0(静電気力が 0 )なので仕事は 0 です。 - 等電位面と電気力線は常に直交しています。
等高線に置き換えて考えてみましょう。電気力線は、電流が流れる道筋と考えることができますので、地形では水の流れに対応させることができます。高いところで水を流すと低い方へ流れて行きます。 そのとき水は最短距離を通って低い方へ流れて行きます。つまり、等高線と直角に流れて行くことになります。 - 等電位面が密なところは電界が強い。
こちらも等高線に置き換えて考えてみましょう。等高線が密集している山の斜面は高低差が激しいところです。等電位面が密ということは、電位の差が大きいということで、電界が強い箇所となります。
電験三種-理論の過去問解説:静電界中の電位と電圧
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2004年(平成16年)問2【電験理論の過去問題】
図のように、電界の強さが E[V/m]の一様な電界中の点Aに 1[C]の正の点電荷をおくと、この点電荷には( ア )が働く。いま、この( ア )に逆らって、その電界中の他の点Bにこの点電荷を移動するには外部から仕事をしてやらなければならない。このような場合、点Bは点Aより電位が( イ )といい、点Aと点Bの間には電位差があるという。電位差の大きさは、点電荷を移動するときに要した仕事の大きさによって決まり、仕事が 1[( ウ )]のとき、2点間の電位差は 1[V]である。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句又は記号として、正しいものを組み合わせたものは次のうちどれか。
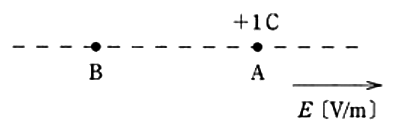

電界の強さ E[V/m]中に +1[C]の点電荷を置いたとき、この正の点電荷が受ける静電気力の大きさと向き F[N]は電界の強さ E[V/m]と同じ値になります。これは、電界(電場)の大きさの定義です。
点電荷が電界に逆らって点Aから点Bに移動したとき、点Bは点Aより電位が高くなります。電位差は点電荷が移動したエネルギーの大きさで、仕事の大きさが 1[J]のとき2点間の電位差は 1[V]になります。
答え (2)
2005年(平成17年)問2【電験理論の過去問題】
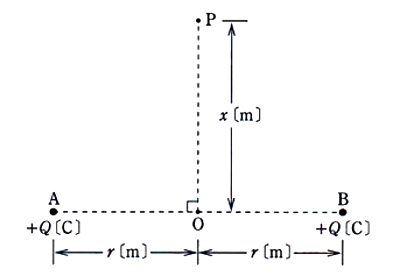
真空中において、図に示すように点Oを通る直線上の、点Oからそれぞれ r[m]離れた2点A,Bに Q[C]の正の点電荷が置かれている。この直線に垂直で、点Oから x[m]離れた点Pの電位 V[V]を表す式として、正しいのは次のうちどれか。
ただし、真空の誘電率を ε0[F/m]とする。
(1) $ \displaystyle \frac{ Q }{2πε_{ 0 } \sqrt{ r^2+x^2}}$ (2) $ \displaystyle \frac{ Q }{2πε_{ 0 } ( r^2+x^2)}$ (3) $ \displaystyle \frac{ Q }{4πε_{ 0 } \sqrt{ r^2+x^2}}$
(4) $ \displaystyle \frac{ Q }{2πε_{ 0 } x^2}$ (5) $ \displaystyle \frac{ Q }{4πε_{ 0 } ( r^2+x^2)}$
点Aの点電荷による点Pの電圧を VA[V]、点Bの点電荷による点Pの電圧を VB[V]とすると、点電荷が作る電位は、
$ V=\displaystyle \frac{ Q}{ 4πε_{ 0 } r }$[V]
なので、
$ V_{ A } =V_{ B } =\displaystyle \frac{ Q }{ 4πε_{ 0 }\sqrt{ r^2+x^2} }$[V]
電位 V[V]はスカラー量なので、$V=V_{ A } +V_{ B }$[V]となります。よって
$ V=\displaystyle \frac{ Q }{2πε_{ 0 } \sqrt{ r^2+x^2}}$[V]
答え (1)
2010年(平成22年)問1【電験理論の過去問題】
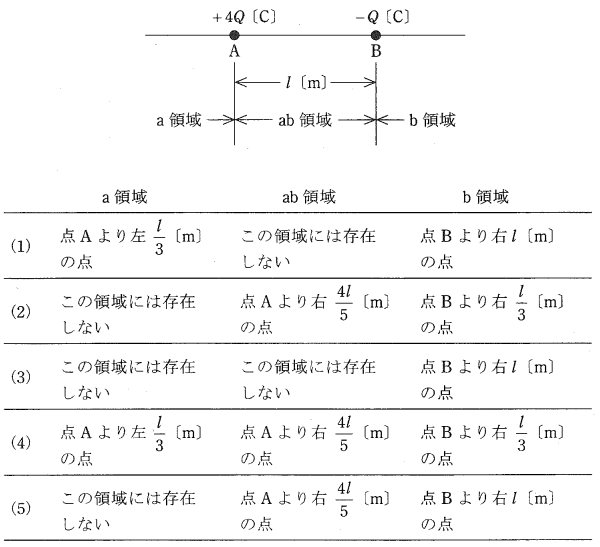
真空中において、図のように点Aに正電荷 +4Q[C]、点Bに負電荷 -Q[C]の点電荷が配置されている。この2点を通る直線上で電位が 0[V]となる点を点Pとする。点Pの位置を示すものとして、正しいものを組み合わせたのは次のうちどれか。なお、無限遠の点は除く。
ただし、点Aと点B間の距離を l[m]とする。また、点Aより左側の領域をa領域、点Aと点Bの間の領域をab領域、点Bより右側の領域をb領域とし、真空の誘電率を ε0[F/m]とする。
点電荷が作る電位の「公式」は
$ V=\displaystyle \frac{ Q}{ 4πε_{ 0 } r }$[V]
aの領域について
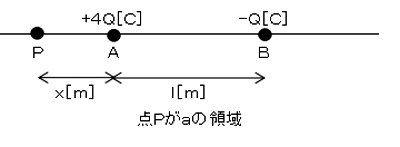
$ V=\displaystyle \frac{ 4Q}{ 4πε_{ 0 } x}+\displaystyle \frac{ -Q}{ 4πε_{ 0 } (x+l) }=0$[V]
$ \displaystyle \frac{ 4}{ x}=\displaystyle \frac{ 1}{ x+l }$
$ x=\displaystyle -\frac{ 4l}{ 3 }$[m]
$x$が負なので、この領域には存在しません。
ab領域について
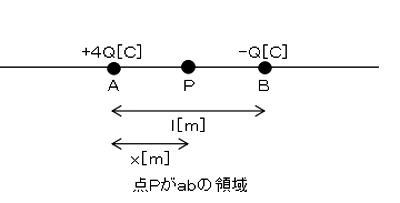
$ V=\displaystyle \frac{ 4Q}{ 4πε_{ 0 } x}+\displaystyle \frac{ -Q}{ 4πε_{ 0 } (l-x) }=0$[V]
$ \displaystyle \frac{ 4}{ x}=\displaystyle \frac{ 1}{ l-x }$
$ x=\displaystyle \frac{ 4l}{ 5 }$[m]
点Aより、右 $\displaystyle \frac{ 4l}{ 5 }$[m]の点になります。
b領域について
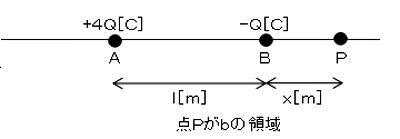
$ V=\displaystyle \frac{ 4Q}{ 4πε_{ 0 } (l+x)}+\displaystyle \frac{ -Q}{ 4πε_{ 0 } x }=0$[V]
$ \displaystyle \frac{ 4}{ l+x}=\displaystyle \frac{ 1}{ x }$
$ x=\displaystyle \frac{ l}{ 3 }$[m]
点Bより、右 $\displaystyle \frac{ l}{ 3 }$[m]の点になります。
答え (2)
2014年(平成26年)問17【電験理論の過去問題】
図のように、真空中において二つの小さな物体A,Bが距離 r[m]を隔てて鉛直線上に置かれている。Aは固定されており、Aの真下にBがある。物体A,Bはそれぞれ、質量 mA[kg],mB[kg]をもち、電荷 +qA[C],-qB[C]を帯びている。qA>0,qB>0とし、真空の誘電率を ε0[F/m]とする。次の(a)及び(b)の問に答えよ。
ただし、小問(a)においては重力加速度 g[m/s2]の重力を、小問(b)においては無重力を、それぞれ仮定する。物体A,Bの間の万有引力は無視する。
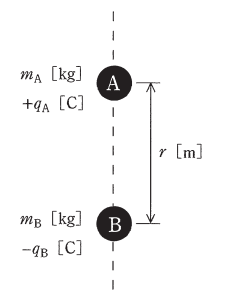
(a) 重力加速度 g[m/s2]の重力のもとでBを初速度零で放ったとき、BはAに近づくように上昇を始めた。このときの条件を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
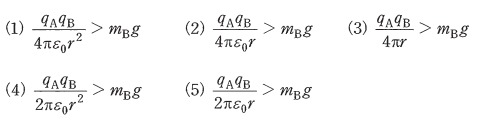
(b) 無重力のもとでBを下向きの初速度 vB[m/s]で放ったとき、Bは下降を始めたが、途中で速度の向きが変わり上昇に転じた。このときの条件を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
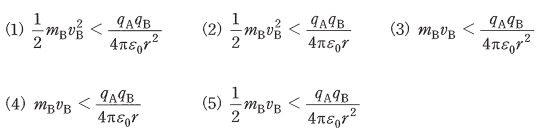
(a) AB間に働く力を F[N]は、クーロンの法則より、
$ F=\displaystyle \frac{ 1 }{ 4πε_{ 0 } }\frac{ q_{ A }q_{ B } }{ r^2}$[N]
AB間に働く力を F[N]は引力です。この引力が物体Bに働く重力の大きさ mBg[N]よりも大きければ、物体Bは物体Aに近づきます。したがって、
$ \displaystyle \frac{ q_{ A }q_{ B } }{4πε_{ 0 } r^2 }>m_Bg$[N]
答え (1)
(b) 静電気力によって、電荷 q[C]が移動するとき、電界 E[V/m]が電荷 q[C]にする仕事W[J]は、(仕事)=(力の大きさ)×(移動距離)と定義されていますので、移動距離を d[m]とすると、
$W=Fd=qEd=q(Ed)$[J]
したがって、
$ W=Fd=\displaystyle \frac{ q_{ A }q_{ B } }{4πε_{ 0 } r^2 }×r$[J]
質量 mB[kg]の物体を、初速度 vB[m/s]で放ったときの運動エネルギーは、$\displaystyle \frac{ 1 }{ 2 }m_Bv_B^2$[J]で表されます。B が上昇するときは、 運動エネルギーの方が小さいときであるので、
$ \displaystyle \frac{ 1 }{ 2 }m_Bv_B^2<\displaystyle \frac{ q_{ A }q_{ B } }{4πε_{ 0 } r }$[J]
答え (2)
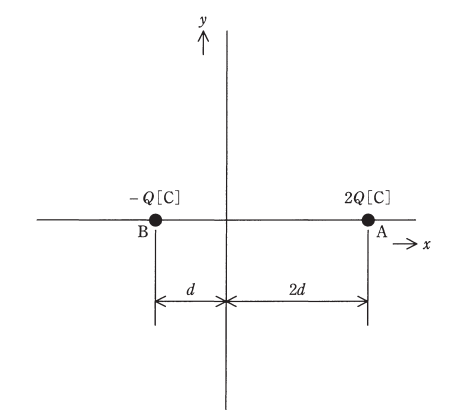
2016年(平成28年)問1【電験理論の過去問題】
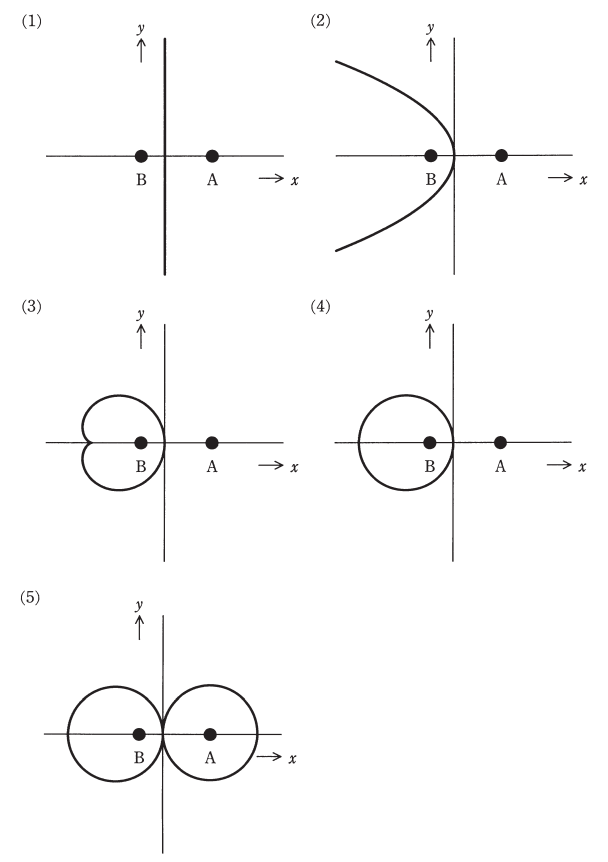
真空中において、図のように x 軸上で、距離 3d[m]隔てた点A(2d,0)、点B(-d,0)にそれぞれ 2Q[C],-Q[C]の点電荷が置かれている。xy平面上で、電位が 0 V となる等電位線を表す図として、最も近いものを次の(1)~(5)のうちから一つ選べ。
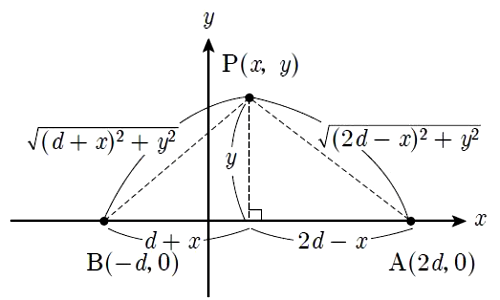
任意の点Pと点A,および点Bまでの距離は次の図のようになります。
点電荷 Q[C]の r[m]離れた地点における、電位 V[V]は次の式で表すことができます。
$ V=\displaystyle \frac{ Q }{ 4πε_{ 0 } r }$[V]
任意の点P(x ,y)の電位を VP[V]とすると、VP[V]は点Aによる点Pの電位 VPA[V]と、点Bによる点Pの電位 VPB[V]のスカラ和になりますので、
$\begin{eqnarray}V_P&=&V_{PA}+V_{PB}\\\\&=&\displaystyle \frac{ 2Q }{ 4πε_{ 0 } AP }+\displaystyle \frac{ -Q }{ 4πε_{ 0 } BP }\\\\&=&\displaystyle \frac{ Q }{ 4πε_{ 0 } }\left(\displaystyle \frac{ 2 }{ \sqrt{ (2d-x)^2+y^2 }}-\displaystyle \frac{ 1 }{ \sqrt{ (d+x)^2+y^2 }}\right)\end{eqnarray} $
VP=0[V]となるには、
$\displaystyle \frac{ 2 }{ \sqrt{ (2d-x)^2+y^2 }}-\displaystyle \frac{ 1 }{ \sqrt{ (d+x)^2+y^2 }}=0$
の時ですので、この式を変形していくと、
$\displaystyle \frac{ 4 }{ (2d-x)^2+y^2 }-\displaystyle \frac{ 1 }{ (d+x)^2+y^2 }=0$
$\ (2d-x)^2+y^2 -4((d+x)^2+y^2)=0$
$\ (x+2d)^2+y^2 =(2d)^2$
この式は、中心(-2d,0)で半径が 2d の円の方程式です。
答え (4)
電験三種の理論科目に出題される「静電気分野」のページ
1.クーロンの法則とは
2.電界とガウスの法則
3.静電界中の電位と電圧
4.静電誘導と誘電分極
5.平行平板コンデンサの静電容量
6.コンデンサの直列接続と並列接続
7.静電エネルギー
8.誘電体とコンデンサ
9.導体球と同心球導体の静電容量






