静電誘導と誘電分極

第三種電気主任技術者（電験三種）試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「静電誘導と誘電分極」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「静電誘導と誘電分極」の過去問題も解説しています。

静電界中の導体

静電誘導

導体を電界中に置くと、導体内の自由電子が電界から力を受け、電界の向きと逆の方向に移動します。自由電子が移動した先の導体の表面には自由電子による負電荷が現れます。また、自由電子が抜けた導体の表面には正電荷が現れます。

このような、電界の影響で自由電子が移動し、導体内の電荷の分布が偏る現象のことを、「静電誘導」といいます。

1. 右向きの一様な電界中に導体を置きます。

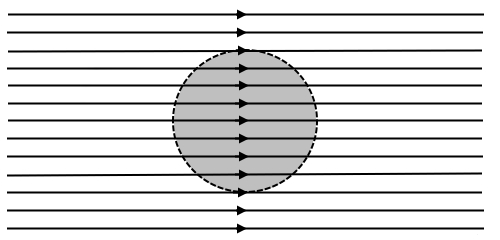
2. 静電誘導によって導体表面に電荷が現れます。現れた電荷によって電界が発生します（静電誘導）。静電誘導によって発生する電界は左向きになります。

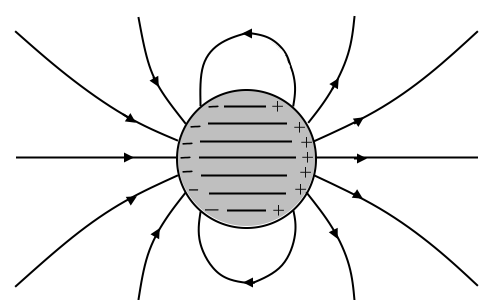
3. 外部電界と静電誘導によって発生する電界を合成した様子です。導体内部では電界は0になります。

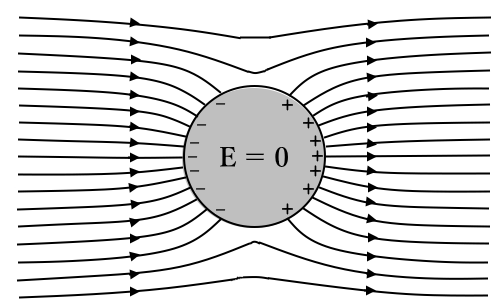
静電遮蔽

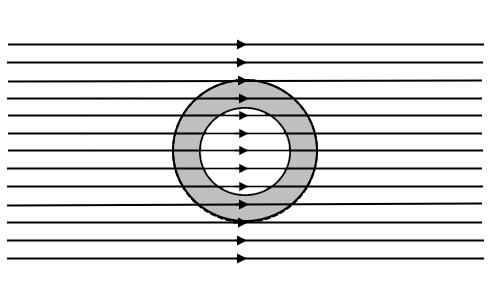
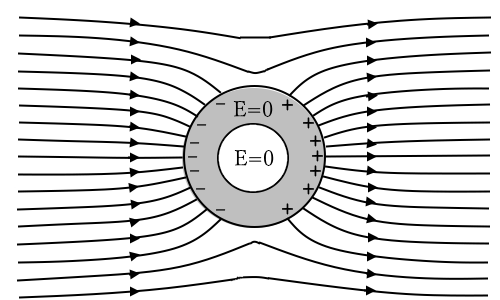
内部に空洞がある導体を電界中に置くと、導体の表面に誘導された電荷の影響で空洞内も電界の強さは0になります。導体の外部表面に誘導された電荷が電場を相殺遮蔽します。導体部分は等電位ですので、等電位に囲まれた空間内の電界は、内部に電荷がなければ0になります。逆をいえば、「空間内部の電場を0にするように導体外表面に電荷が誘導する」といった状況になります。

このように、物体を導体で囲んで外部の電界をさえぎる現象を「静電遮蔽］といいます。

正の点電荷を置いた場合

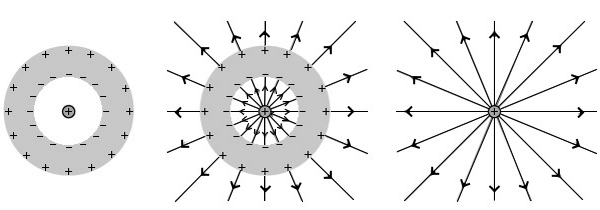
内部に空洞がある導体の中空部に正の点電荷を置いた場合、自由電子の影響で中空導体の内側表面には負電荷が、外側表面に正電荷が現れます。電気力線は中空導体が無い場合と同じです。

導体を接地した場合

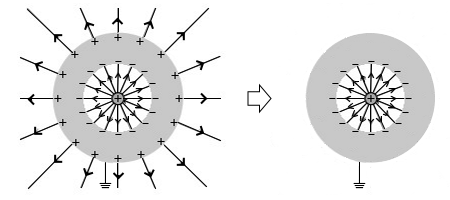
導体を接地すると正電荷はアースへ逃げていき、導体外側の電気力線は無くなります。内側表面の負電荷は、中央の正電荷と引き合っているので動きません。

接地することによって中空部分に存在する帯電体の影響が外部に及ばなくなります。これも静電遮蔽といいます。

静電界中の絶縁体と誘電分極

この影響で個々の原子は、電界の方向に偏りが生じます。この現象を「分極」といいます。この分極のしやすさを「誘電率」として表します。

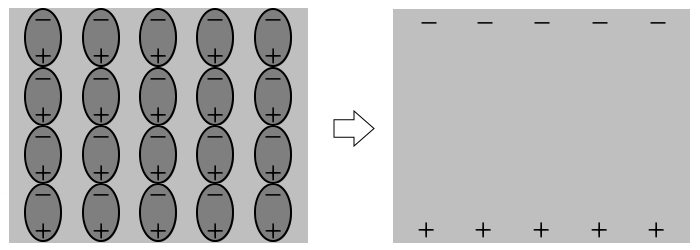
絶縁体内で分極が全体的に起こり偏りが一定方向にそろうと、個々の原子は隣同士で電荷を打ち消し合います。ただし、一番端は打ち消しあう相手がいないので、表面に電荷が発生します。このように、分極によって絶縁体全体の電荷が偏ることを「誘電分極」といい、誘電分極を起こす物質を「誘電体」といいます。

誘電体はコンデンサの材料に使われています。誘電分極が起こりやすい（誘電率の大きい）物質をコンデンサに使用すると、多くの電荷を溜めることができます。

誘電分極が起こると誘電体内部の電界の強さは小さくなります。これは、誘電分極をするためにエネルギーが使われるからです。尚、誘電分極による電荷は、電流として外に取り出すことはできません。

　　

電験三種－理論の過去問解説：静電誘導と誘電分極

(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。

2001年（平成13年）問2【電験理論の過去問題】

静電界に関する次の記述のうち、誤っているのはどれか。

1. 媒質中に置かれた正電荷から出る電気力線の本数は、その電荷の大きさに比例し、媒質の誘電率に反比例する。
2. 電界中における電気力線は、相互に交さしない。
3. 電界中における電気力線は、等電位面と交差する。
4. 電界中のある点の電気力線の密度は、その点における電界の強さ(大きさ)を表す。
5. 電界中に置かれた導体内部の電界の強さ(大きさ)は、その導体表面の電界の強さ(大きさ)に等しい。

2009年（平成21年）問2【電験理論の過去問題】

静電界に関する記述として、正しいのは次のうちどれか。

1. 二つの小さな帯電体の間に働く力の大きさは，それぞれの帯電体の電気量の和に比例し，その距離の２乗に反比例する。
2. 点電荷が作る電界は点電荷の電気量に比例し，距離に反比例する。
3. 電気力線上の任意の点での接線の方向は，その点の電界の方向に一致する。
4. 等電位面上の正電荷には，その面に沿った方向に正のクーロンカが働く。
5. コンデンサの電極板間にすき間なく誘電体を入れると，静亀容量と電極板間の電界は，誘電体の誘電率に比例して増大する。

2011年（平成23年）問1【電験理論の過去問題】

静電界に関する記述として、誤っているものを次の(1)～(5)のうちから一つ選べ。

1. 電気力線は、導体表面に垂直に出入りする。
2. 帯電していない中空の球導体Bが接地されていないとき、帯電した導体Aを導体Bで包んだとしても、導体Bの外部に電界ができる。
3. Q［C］の電荷から出る電束の数や電気力線の数は、電荷を取り巻く物質の誘電率 ε［F/m］によって異なる。
4. 導体が帯電するとき、電荷は導体の表面にだけ分布する。
5. 導体内部は等電位であり、電界は零である。

2014年（平成26年）問2【電験理論の過去問題】

次の文章は、静電気に関する記述である。

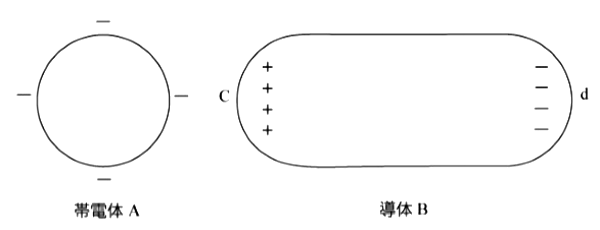
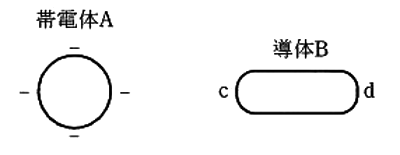
図のように真空中において、負に帯電した帯電体Aを、帯電していない絶縁された導体Bに近づけると、導体Bの帯電体Aに近い側の表面ｃ付近に（　ア　）の電荷が現れ、それと反対側の表面ｄ付近に（　イ　）の電荷が現れる。この現象を（　ウ　）という。

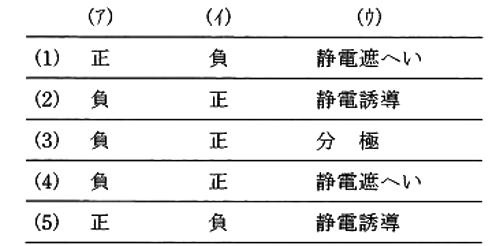
上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。