このページでは、変圧器の並行(並列)運転と負荷分担について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の電力科目の試験で、実際に出題された変圧器の並行(並列)運転と負荷分担の過去問題も解説しています。
変圧器の並行運転
2台以上の変圧器を、一次側および二次側のそれぞれを並列に接続して運転するには、一定の条件を満たす必要があります。
- 単相器は極性が合っていること
(極性とは、一次巻線に対する二次巻線の誘起電圧の方向です。 ) - 三相器は角変位が合っていること
(角変位とは、一次側の線間電圧に対して二次側の線間電圧の位相が遅れる角度です。) - 三相器は相回転(相順)が合っていること
- 一次側と二次側の定格電圧がなるべく等しいこと
(変圧器の巻数比が等しいこと) - インピーダンスがなるべく定格容量に逆比例していること
(定格容量基準の%Zが等しいこと) - 抵抗とリアクタンスの比がなるべく等しいこと
参考:同期発電機の並行運転の条件
- 電圧が等しい
- 周波数が等しい
- 位相が等しい
- 波形が等しい
- 相回転が等しい
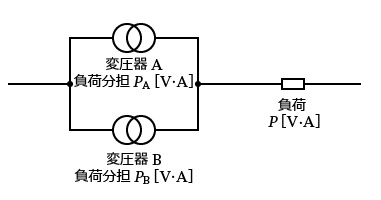
変圧器の負荷分担
並行運転している各変圧器が分担する負荷は、インピーダンスに逆比例して配分されます。インピーダンスが、百分率インピーダンス(%Z)で与えられたときは、各 %Z を同一基準容量に換算した値によって、逆比例の配分計算をします。
変圧器 A、Bが分担する負荷容量を求める式
$P_A=P×\displaystyle \frac{ \displaystyle \frac{ P_{An} }{ \%Z_A } }{ \displaystyle \frac{ P_{An} }{ \%Z_A }+\displaystyle \frac{ P_{Bn} }{ \%Z_B } }$
$P_B=P×\displaystyle \frac{ \displaystyle \frac{ P_{Bn} }{ \%Z_B } }{ \displaystyle \frac{ P_{An} }{ \%Z_A }+\displaystyle \frac{ P_{Bn} }{ \%Z_B } }$
PAn[V・A]:変圧器Aの定格容量
PBn[V・A]:変圧器Bの定格容量
%ZA[%]:変圧器Aの%インピーダンス
%ZB[%]:変圧器Bの%インピーダンス
変圧器の二次側電圧が異なる場合、循環電流 IC[A]が流れます。
$I_C=\displaystyle \frac{ E_A-E_B }{ Z_A+Z_B }$
電験三種-電力(変電所)過去問題
2004年(平成16年)問9
同期発電機を電力系統に並列する際、電力系統と一致させなければならない条件がある。その条件として正しいものを組み合わせたものは次のうちどれか。
- 電圧,力率,周波数
- 電流,位相,インピーダンス
- 電圧,位相,周波数
- 電流,力率,周波数
- 電圧,力率,インピーダンス
2004年(平成16年)問9 過去問解説
同期発電機の並行運転の条件は、
- 電圧が等しい
- 周波数が等しい
- 位相が等しい
- 波形が等しい
- 相回転が等しい
答え(3)
2005年(平成17年)問16
容量 15[MV・A]、変圧比 33[kV]/6.6[kV]、百分率インピーダンス降下が自己容量基準で 5[%]であるA変圧器と、容量 8[MV・A]、変圧比 33[kV]/6.6[kV]、百分率インピーダンス降下が自己容量基準で 4[%]であるB変圧器とを並行運転している変電所がある。これについて次の(a)及び(b)に答えよ。
ただし、各変圧器の抵抗とリアクタンスの比は等しいものとする。
(a) 12[MV・A]の負荷を加えたとき、A変圧器の分担する負荷[MV・A]の値としい、正しいのは次のうちどれか。
(1) 4.8 (2) 5.3 (3) 6.7 (4) 7.2 (5) 7.8
(b) 並行運転している2台の変圧器が負担できる最大負荷容量[MV・A]の値として、正しいは次のうちどれか。
(1) 20 (2) 21 (3) 22 (4) 23 (5) 25
2005年(平成17年)問16 過去問解説
(a) A変圧器の分担負荷 PA[MV・A]は、
$\begin{eqnarray}P_A&=&P×\displaystyle \frac{ \displaystyle \frac{ P_{An} }{ \%Z_A } }{ \displaystyle \frac{ P_{An} }{ \%Z_A }+\displaystyle \frac{ P_{Bn} }{ \%Z_B } }\\\\ &=& 12×\displaystyle \frac{ \displaystyle \frac{ 15 }{ 5 } }{ \displaystyle \frac{ 15 }{ 5 }+\displaystyle \frac{ 8 }{ 4 }}\\\\&=&7.2[MV・A]\end{eqnarray}$
答え (4)
(b) B変圧器の分担負荷 PB[MV・A]は、
$\begin{eqnarray}P_B&=&P×\displaystyle \frac{ \displaystyle \frac{ P_{Bn} }{ \%Z_B } }{ \displaystyle \frac{ P_{An} }{ \%Z_A }+\displaystyle \frac{ P_{Bn} }{ \%Z_B } }\\\\ &=& 12×\displaystyle \frac{ \displaystyle \frac{ 8 }{ 4 } }{ \displaystyle \frac{ 15 }{ 5 }+\displaystyle \frac{ 8 }{ 4 }}\\\\ &=&4.8[MV・A]\end{eqnarray}$
A変圧器とB変圧器の分担率は
A変圧器:$\displaystyle \frac{ 7.2 }{ 15}×100 =48$[%]
B変圧器:$\displaystyle \frac{ 4.8}{ 8}×100=60$[%]
B変圧器の方が分担率が高く、また容量が小さいので、先に容量がいっぱいになります。つまり、B変圧器は、8[MV・A]使用し、残りをA変圧器が負担します。A変圧器の負担分は $8×\displaystyle \frac{ 7.2}{ 4.8}$ [MV・A]で表すことができますので、
$Pmax = 8 + 8×\displaystyle \frac{ 7.2}{ 4.8}=20$[MV・A]
答え (1)
2010年(平成22年)問16
定格容量 80[MV・A]、一次側定格電圧 33[kV]、二次側定絡電圧 11[kV]、百分率インピーダンス 18.3[%](定格容量ベース)の三相変圧器 TA がある。三相変圧器 TA の一次側は 33[kV]の電源に接続され、二次側は負荷のみが接続されている。電源の百分率内部インピーダンスは、1.5[%](系統基準容量 80[MV・A]ベース)とする。なお、抵抗分及びその他の定数は無視する。
次の(a)及び(b)に答えよ。
(a) 将来の負荷変動等は考えないものとすると,変圧器の TA の二次側に設置する遮断器の定格遮断電流の値[kA]として、最も適切なものは次のうちどれか。
(1) 5 (2) 8 (3) 12.5 (4) 20 (5) 25
(b) 定格容量 50[MV・A]、百分率インピーダンスが 12.0[%]の三相変圧器 TB を三相変圧器 TA と並列に接続した。40[MW]の負荷をかけて運転した場合、三相変圧器 TA の負荷分担[MW]の値として、正しいのは次のうちどれか。
ただし、三相変圧器群 TA と TB にはこの負荷のみが接続されているものとし、抵抗分及びその他の定数は無視する。
(1) 15.8 (2) 19.5 (3) 20.5 (4) 24.2 (5) 24.6
2010年(平成22年)問16 過去問解説
(a) 基準容量 PB と基準電圧 VB から、定格電流 In を計算します。
$\begin{eqnarray}P_B&=&\sqrt{ 3 } V_BI_n\\&=&\sqrt{ 3 } ×11×10^3×I_n\\&=&80×10^6\end{eqnarray}$
$I_n=\displaystyle \frac{ 80×10^6 }{ \sqrt{ 3 } ×11×10^3}=4200$[A]
三相短絡電流 IS を計算します。
$\begin{eqnarray}I_S&=&I_n×\displaystyle \frac{ 100 }{ \%X }\\&=&4200×\displaystyle \frac{ 100 }{ 18.3+1.5}\\&=&21.2[kA]\end{eqnarray}$
遮断器の定格遮断電流の値は、21.2 より大きい直近の値 25 となります。
答え (5)
(b) A変圧器の分担負荷 PA[MV・A]は、
$\begin{eqnarray}P_A&=&P×\displaystyle \frac{ \displaystyle \frac{ P_{An} }{ \%Z_A } }{ \displaystyle \frac{ P_{An} }{ \%Z_A }+\displaystyle \frac{ P_{Bn} }{ \%Z_B } }\\\\ &=& 40×\displaystyle \frac{ \displaystyle \frac{ 80 }{ 18.3 } }{ \displaystyle \frac{ 80 }{ 18.3 }+\displaystyle \frac{ 50 }{ 12.0 }}\\\\ &=&20.5[MV・A]\end{eqnarray}$
答え (3)
2014年(平成26年)問6
1バンクの定格容量 25MV・Aの三相変圧器を 3バンク有する配電用変電所がある。変圧器 1バンクが故障した時に長時間の停電なしに故障発生前と同じ電力を供給したい。
この検討に当たっては、変圧器故障時には、他の変電所に故障発生前の負荷の 10%を直ちに切り換えることができるとともに、残りの健全な変圧器は、定格容量の 125%まで過負荷することができるものとする。
力率は常に 95%(遅れ)で変化しないものとしたとき、故障発生前の変電所の最大総負荷の値[MW]として、
最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 32.9 (2) 53.4 (3) 65.9 (4) 80.1 (5) 98.9
2014年(平成26年)問6 過去問解説
故障発生時には 2バンクを定格容量の 125%まで負荷を掛けることができるので、容量 P[MW]は、
P=25×2×1.25×0.95=59.375[MW]
故障発生前の負荷の 10%を直ちに切り替えることができるので P=0.9P’ [MW]となり、
0.9P’=59.375
P’=65.97[MW]
答え(3)
2016年(平成28年)問6
一次側定格電圧と二次側定格電圧がそれぞれ等しい変圧器Aと変圧器Bがある。変圧器Aは、定格容量 SA=5000kV・A、パーセントインピーダンス %ZA=9.0%(自己容量ベース)、変圧器Bは、定格容量 SB=1500kV・A、パーセントインピーダンス %ZB=7.5%(自己容量ベース)である。この変圧器2台を並行運転し、6000kV・Aの負荷に供給する場合、過負荷となる変圧器とその変圧器の過負荷運転状態[%](当該変圧器が負担する負荷の大きさをその定格容量に対する百分率で表した値)の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| 過負荷となる変圧器 | 過負荷運転状態 [%] | |
| (1) | 変圧器A | 101.5 |
| (2) | 変圧器B | 105.9 |
| (3) | 変圧器A | 118.2 |
| (4) | 変圧器B | 137.5 |
| (5) | 変圧器A | 173.5 |
2016年(平成28年)問6 過去問解説
変圧器Aの分担負荷 PA[MV・A]、変圧器Bの分担負荷 PB[MV・A]は、
$\begin{eqnarray}P_A&=&P×\displaystyle \frac{ \displaystyle \frac{ P_{An} }{ \%Z_A } }{ \displaystyle \frac{ P_{An} }{ \%Z_A }+\displaystyle \frac{ P_{Bn} }{ \%Z_B } }\\\\ &=& 6000×\displaystyle \frac{ \displaystyle \frac{ 5000 }{ 9 } }{ \displaystyle \frac{ 5000 }{ 9 }+\displaystyle \frac{ 1500 }{ 7.5 }}\\\\ &=&4412[kV・A]\end{eqnarray}$
$\begin{eqnarray}P_B&=&P×\displaystyle \frac{ \displaystyle \frac{ P_{Bn} }{ \%Z_B } }{ \displaystyle \frac{ P_{An} }{ \%Z_A }+\displaystyle \frac{ P_{Bn} }{ \%Z_B } }\\\\ &=& 6000×\displaystyle \frac{ \displaystyle \frac{ 1500 }{ 7.5 } }{ \displaystyle \frac{ 5000 }{ 9 }+\displaystyle \frac{ 1500 }{ 7.5 }}\\\\ &=&1588[kV・A]\end{eqnarray}$
変圧器Aは定格容量 5000[kV・A]に対して負荷分担は 4412[kV・A]です。変圧器Bは定格容量 1500[kV・A]に対して負荷分担は 1588[kV・A]です。したがって、変圧器Bが過負荷となります。 変圧器Bの過負荷率は、
$\displaystyle \frac{ 1588 }{ 1500 }×100=105.9$[%]
答え (2)





