第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される直流回路の消費電力について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された直流回路の消費電力の過去問題も解説しています。
ジュールの法則
抵抗に電流を流すと熱が発生します。これは、抵抗内で消費されるエネルギーは、すべて熱エネルギーに変換されるからです。そのことを表す法則を言葉で表すと次のようになります。
抵抗に流れる電流によって単位時間中に発生する熱量は、電流の2乗と抵抗の積に比例する。
この法則をジュールの法則といい、式で表すと次のようになります。
ジュールの法則:抵抗 $R$ に、電流 $I$ が $t$ 秒間流れたときに発生する熱量 $Q$ を求める式
$Q=I^2Rt$
$Q$[J]:抵抗に発生する熱量
$I$[A]:抵抗に流れる電流
$R$[Ω]:抵抗
$t$[秒]:電流が流れる時間
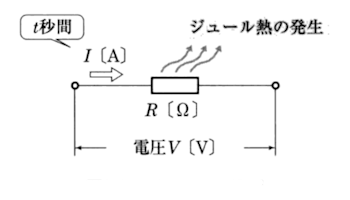
また、オームの法則 $I=\displaystyle \frac{V}{R}$ を、ジュールの法則 $Q=I^2Rt$ に代入すると、次の式も成り立ちます。
$Q=VIt$
電線の電気抵抗
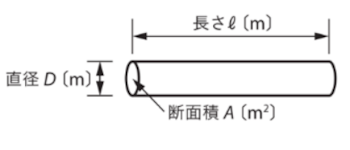
電線の電気抵抗は、電線の材質・太さ・長さなどによって変わります。同じ導体の電気抵抗の大きさは、長さに $l$[m]に比例し、断面積 $A$[m2]に反比例します。
電線の電気抵抗
電線の電気抵抗を求める式
$R=ρ\displaystyle \frac{i}{A}$
$R$[Ω]:抵抗
$A$[m2]:断面積
$l$[m]:長さ
$ρ$[Ω・m]:抵抗率
$ρ$(ロー)は、電気の通しにくさを表す定数で抵抗率といいます。電気の通しやすさを表す定数が $σ$(シグマ)で、導電率といいます。導電率 $σ$ は、抵抗率 $ρ$ の逆数です。
$導電率σ=\displaystyle \frac{1}{抵抗率ρ}$
電力と電力量
電流が1秒当たりにする仕事のことを電力(消費電力)といいます。電流がする仕事の仕事率のことです。電力は、仕事率と同じように記号を $P$ で表します。単位は[W]ワット を用います。
電力は、電圧 $V$ と電流 $I$ の積「$P=V×I$」で求めることができます。オームの法則 $V=RI$ を用いると、次のように表すことができます。
電力 $P$ を求める式
$P=VI$ ・・・「電圧」と「電流」から電力を求める式
$P=I^2 R$ ・・・「電流」と「抵抗」から電力を求める式
$P= \displaystyle \frac{V^2}{R}$・・・「電圧」と「抵抗」から電力を求める式
$P$[W]:電力
$V$[V]:抵抗にかかる電圧
$I$[A]:抵抗に流れる電流
$R$[Ω]:抵抗
電力量
抵抗にある時間だけ電力を加えたときのエネルギー量を「電力量」と言い、記号を $W$ で表します。単位は [W・s]ワット秒 または、[W・h]ワット時を使用します。
電力量 $W$ を求める式は、次のようになります。
電力量 $W$ を求める式
$W=Pt$
$W$[W・s]または[W・h]:電力量
$P$[W]:電力
$t$[s]または[h]:電流が流れる時間
また、電力 $P$ を求める式 $P=VI$、$P=I^2 R$、$P= \displaystyle \frac{V^2}{R}$ より、電力量を求める式は、次のように表すことができます。
$W=VIt$、$W=I^2 Rt$、$W= \displaystyle \frac{V^2}{R}t$
電力量 $W$ を求める式は、熱量 $Q$ を求める式と同じになりますので、$Q=Pt$ も成り立ちます。ただし、熱量 $Q$ と 電力量 $W$ と熱量 $Q$ の単位は[W・s]と[J]で、違うものになります。
電験三種-理論の過去問解説:直流回路の消費電力
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1998年(平成10年)問11【電験理論の過去問題】
二つの抵抗 $R_1$[Ω]及び $R_2$[Ω]を図1のように並列に接続した場合の全消費電力は、これら二つの抵抗を図2にように直列に接続した場合の全消費電力の 6倍であった。このとき、$R_2$ の値として、正しいものは次のうちどれか。ただし、$R_1=1$[Ω],$R_2>R_1$ とし、電源 $E$ の内部抵抗は無視するものとする。
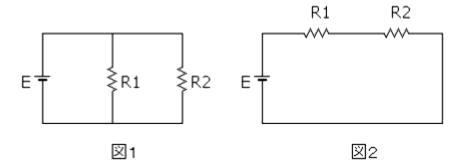
(1) 1.1 (2) 1.4 (3) 2.0 (4) 3.7 (5) 4.3
図1の回路の消費電力を $P_1$[W]、図2の回路の消費電力を $P_2$[W]とすると、$P=\displaystyle \frac{ E^2 }{ R}$ より
$P_1=\displaystyle \frac{ E^2 }{ \displaystyle \frac{ R_1R_2 }{ R_1+R_2}}=\displaystyle \frac{ (R_1+R_2)E^2 }{ R_1R_2 }$
$P_2=\displaystyle \frac{ E^2 }{ R_1+R_2}$
題意より、$P_1=6P_2$ なので、
$\displaystyle \frac{ (R_1+R_2)E^2 }{ R_1R_2 }=\displaystyle \frac{ 6E^2 }{ R_1+R_2}$
$(R_1+R_2)^2 =6R_1R_2$
$R_1=1$[Ω]なので、
$(1+R_2)^2 =6R_2$
$R_2^2-4R_2+1=0$
$R_2=\displaystyle \frac{ 4±\sqrt{ 16-4 } }{ 2}=\displaystyle \frac{ 4±2\sqrt{ 3 } }{ 2}=2±\sqrt{ 3 }$
$R_2>R_1$ なので、$R_2=2+\sqrt{ 3 }≒3.7$[Ω]
答え (4)
1999年(平成11年)問6【電験理論の過去問題】
図の $L$ 及び $C$ を含む直流回路において、$L$ 及び $C$ に蓄えられるエネルギーの合計値[J]として、正しいのは次のうちどれか。
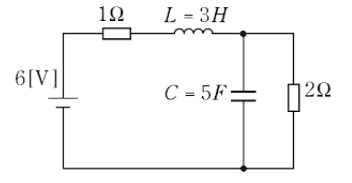
(1) 6 (2) 30 (3) 46 (4) 54 (5) 80
電源が直流ですので、定常状態では $L$ は短絡状態、$C$ は開放状態になります。回路に流れる電流を $I$[A]、2[Ω]の抵抗に加わる電圧を $V$[V]とすると、オームの法則と分圧の法則より
$I=\displaystyle \frac{ 6}{ 1+2}=2$[A]
$V=\displaystyle \frac{ 2}{ 1+2}×6=4$[V]
$L$ 及び $C$ に蓄えられるエネルギーをそれぞれ、$W_L$,$W_C$[J]とすると、
$W_L=\displaystyle \frac{ 1}{ 2}LI^2=\displaystyle \frac{ 1}{ 2}×3×2^2=6$[J]
$W_C=\displaystyle \frac{ 1}{ 2}LV^2=\displaystyle \frac{ 1}{ 2}×5×4^2=40$[J]
したがって、$L$ 及び $C$ に蓄えられるエネルギーの合計値 $W$[J]は、
$W=W_L+W_C=46$[J]
答え (3)
2002年(平成14年)問12【電験理論の過去問題】
図1の抵抗回路において、抵抗 $R$[Ω]の消費する電力は 72[W]である。このときの pq 端子の電圧 $V$[V]をもとめる。次の(a)及び(b)に答よ。
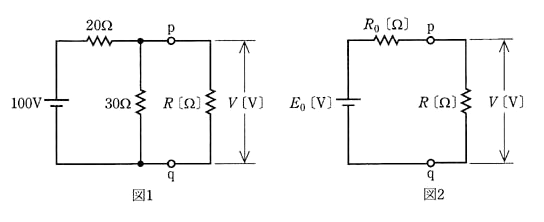
(a) 図1の pq 端子から左側を見た回路は図2に示すように、電圧源 $E_0$[V]と内部抵抗 $R_0$[Ω]の電源回路に置き換えることができる。$E_0$[V]と $R_0$[Ω]の値として、正しいのは次のうちどれか。
(1) $E_0=40$[V],$R_0=6$[Ω]
(2) $E_0=60$[V],$R_0=12$[Ω]
(3) $E_0=100$[V],$R_0=20$[Ω]
(4) $E_0=60$[V],$R_0=30$[Ω]
(5) $E_0=40$[V],$R_0=50$[Ω]
(b) 抵抗 $R$[Ω]が 72[W]を消費するときの $R$[Ω]の値には二つある。それぞれに対応した電圧 $V$[V]のうち、高い方の電圧 $V$[V]の値として正しいのはどれか。
(1) 36 (2) 50 (3) 72 (4) 84 (5) 100
(a) テブナンの定理を利用します。電圧源は短絡し、端子 pq から左側の回路を見た合成抵抗 $R_0$[Ω]は、
$R_0=\displaystyle \frac{ 20×30}{ 20+30}=12$[Ω]
端子 pq 間を開放したときの端子間電圧 $E_0$[V]は、分圧の法則より
$E_0=\displaystyle \frac{ 100}{ 20+30}×30=60$[V]
答え (2)
(b) 抵抗 $R$ に流れる電流を $I$[A]とすると、テブナンの定理より、
$I=\displaystyle \frac{ V_0 }{ R_0+R }=\displaystyle \frac{ 60 }{ 12+R }$
消費電力は $P=RI^2$[W]で表されます。題意より、$P=72$[W]なので、
$R×\displaystyle \frac{ 60 ^2}{ (12+R)^2 }=72$
この式を $R$ について解きます。
$R^2+24R+144=50R$
$R^2-26R+144=0$
$(R-8)(R-18)=0$
$R=8,18$ [Ω]
$R=8$[Ω]のときは $I=3$[A]で、そのときの電圧は 24[V]
$R=18$[Ω]のときは $I=2$[A]で、そのときの電圧は 36[V]
高い方の電圧は 36[V]
答え (1)
2007年(平成19年)問5【電験理論の過去問題】
起電力が $E$[V]で内部抵抗が $r$[Ω]の電池がある。この電池に抵抗 $R_1$[Ω]と可変抵抗 $R_2$[Ω]を並列につないだとき、抵抗 $R_2$[Ω]から発生するジュール熱が最大となるときの抵抗 $R_2$[Ω]の値を示す式として、正しいのは次のうちどれか。
(1) $R_2=r$ (2) $R_2=R_1$ (3) $R_2=\displaystyle \frac{ rR_1}{ (r-R) }$ (4) $R_2=\displaystyle \frac{ rR_1}{ (R_1-r) }$ (5) $R_2=\displaystyle \frac{ rR_1}{ (r+R_1) }$
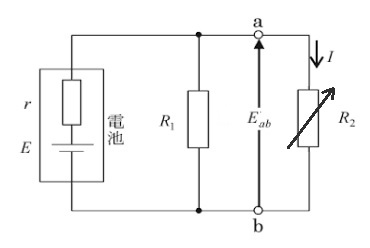
図に示す回路で、テブナンの定理を利用します。電圧源は短絡し、端子 ab から左側の回路を見た合成抵抗 $R_0$[Ω]は、
$R_0=\displaystyle \frac{ R_1r}{ R_1+r}$[Ω]
端子 ab 間を開放したときの端子間電圧 $E_{ab}$[V]は、分圧の法則より
$E_{ab}=\displaystyle \frac{ R_1}{ R_1+r}×E$[V]
抵抗 $R_2$ に流れる電流を $I$[A]とすると、テブナンの定理より、
$\begin{eqnarray}I&=&\displaystyle \frac{ E_{ab} }{ R_0+R_2 }\\\\&=&\displaystyle \frac{ \displaystyle \frac{ ER_1}{ R_1+r} }{ \displaystyle \frac{ R_1r}{ R_1+r}+R_2 }\\\\&=&\displaystyle \frac{ ER_1}{R_1r+ R_2(R_1+r) }\end{eqnarray}$
可変抵抗 $R_2$[Ω]の消費電力 $P$[W]は、
$P=R_2I^2=R_2\left(\displaystyle \frac{ ER_1}{ R_1r+ R_2(R_1+r) }\right)^2$
消費電力 $P$[W]が最大になるときの条件は、分母が最小になるときです。最小の定理より、
$R_1r= R_2(R_1+r) $
$R_2=\displaystyle \frac{ rR_1}{ (r+R_1)}$
答え (5)
最小の定理
$a、b$ の2つの数があって、その積 $ab$ が一定であれば、$a=b$ のとき、和 $a+b$ が最小となります。
最大の定理
$a、b$ の2つの数があって、その和 $a+b$ が一定であれば、$a=b$ のとき、積 $ab$ は最大となります。
2010年(平成22年)問5【電験理論の過去問題】
図の直流回路において、12[Ω]の抵抗の消費電力が 27[W]である。このとき、抵抗 $R$[Ω]の値として、正しいのは次のうちどれか。
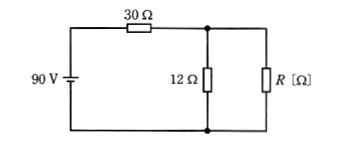
(1) 4.5 (2) 7.5 (3) 8.6 (4) 12 (5) 20
消費電力は $P=RI^2$[W]で表されます。この式を変形すると、
$I=\displaystyle \sqrt{ \frac{ P}{ R}}$
12[Ω]の抵抗に流れる電流を $I$[A]とすると、
$I=\displaystyle \sqrt{ \frac{ 27}{ 12}}=1.5$[A]
回路全体の合成抵抗を $R_Z$[Ω]とすると、
$R_Z=30+\displaystyle \frac{ 12R}{12+R}$
12[Ω]の抵抗に流れる電流を $I$[A]を 抵抗 $R$ で表します。分流の法則より、
$\begin{eqnarray}I&=&\displaystyle \frac{ R}{12+R}×\displaystyle \frac{ 90}{R_Z}\\\\&=&\displaystyle \frac{ R}{12+R}×\displaystyle \frac{ 90}{30+\displaystyle \frac{ 12R}{12+R}}\\\\&=&\displaystyle \frac{ 90R}{360+42R}\\\\&=&1.5[A]\end{eqnarray}$
$27R=540$
$R=20$[Ω]
答え (5)
2013年(平成25年)問6【電験理論の過去問題】
図の直流回路において、抵抗 $R=10$[Ω]で消費される電力[W]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
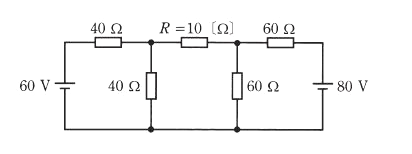
(1) 0.28 (2) 1.89 (3) 3.79 (4) 5.36 (5) 7.62
テブナンの定理を利用します。端子 ab 間を開放したときの端子間電圧 $V_0$[V]を、図に示す $V_a$[V]と $V_b$[V]から導きます。
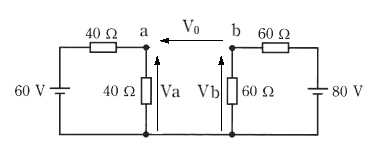
分圧の法則より、
$V_a=\displaystyle \frac{ 40}{40+40}×60=30$ [V]
$V_b=\displaystyle \frac{ 80}{60+60}×60=40$ [V]
$V_0=V_b-V_a=40-30=10$[V]
電圧源を短絡し、端子 ab から見た合成抵抗を $R_0$[Ω]とします。等価回路図は次のようになります。
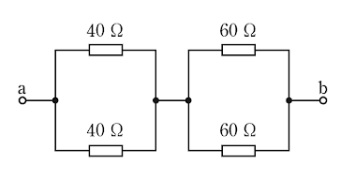
$R_0=\displaystyle \frac{ 40}{2}+\displaystyle \frac{ 60}{2}=50$[Ω]
抵抗 $R$ に流れる電流を $I$[A]とすると、テブナンの定理より、
$I=\displaystyle \frac{ V_0 }{ R_0+R }=\displaystyle \frac{ 10 }{ 50+10 }=\displaystyle \frac{ 1 }{ 6 }$[A]
抵抗 $R$ の消費電力は $P$[W]は、
$P=RI^2=10×\left(\displaystyle \frac{ 1 }{ 6 }\right)^2≒0.28$[W]
答え (1)
2014年(平成26年)問7【電験理論の過去問題】
図に示す直流回路において、抵抗 $R_1=5$ Ω で消費される電力は抵抗 $R_3=15$ Ω で消費される電力の何倍となるか。その倍率として、最も近い値を次の(1)~(5)のうちから一つ選べ。
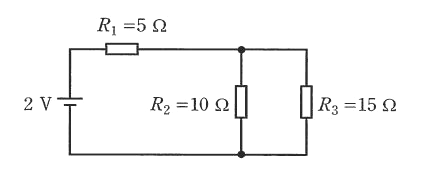
(1) 0.9 (2) 1.2 (3) 1.5 (4) 1.8 (5) 2.1
抵抗 $R_1$ に流れる電流を $I$[A]、抵抗 $R_3$ に流れる電流を $I_3$[A]とすると、分流の法則 より
$I_3=\displaystyle \frac{10I }{ 10+15 }=\displaystyle \frac{2I }{ 5 }$
消費電力は $P=RI^2$[W]で表されます。抵抗 $R_1$ で消費される電力を $P_1$[W]、抵抗 $R_3$ で消費される電力を $P_3$[W]とすると、消費される電力比 $\displaystyle \frac{P_1 }{ P_3 } $ は、
$\displaystyle \frac{P_1 }{ P_3 } =\displaystyle \frac{5I^2 }{ 15×\left(\displaystyle \frac{2I }{ 5 }\right)^2 }=\displaystyle \frac{25 }{ 12 } ≒2.08$
答え (5)
2016年(平成28年)問5【電験理論の過去問題】
図のように、内部抵抗 $r=0.1$ Ω、起電力 $E=9$ V の電池4個を並列に接続した電源に抵抗 $R=0.5$ Ω の負荷を接続した回路がある。この回路において、抵抗 $R=0.5$ Ω で消費される電力の値[W]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
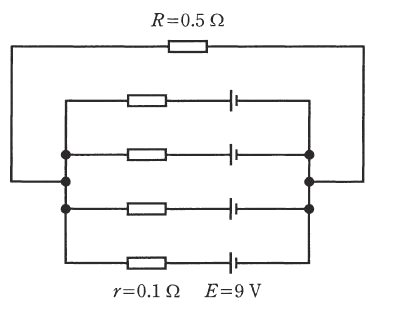
(1) 50 (2) 147 (3) 253 (4) 820 (5) 4050
テブナンの定理を利用します。
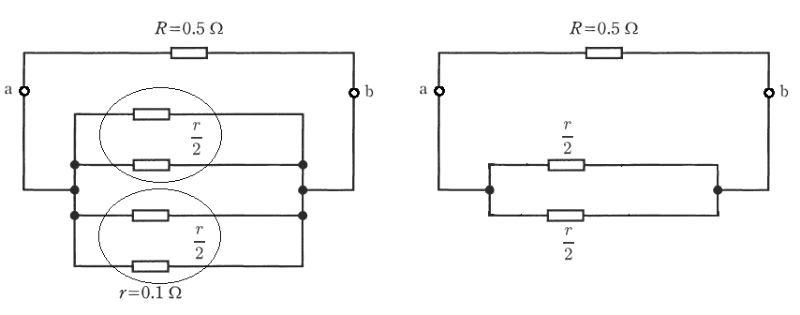
電圧源は短絡し、端子 ab から下側を見た合成抵抗 $R_0$[Ω]は、
$R_0=\displaystyle \frac{ r}{4}=0.025$[Ω]
端子 ab 間を開放したときの端子間電圧 $V_0$[V]を求めます。
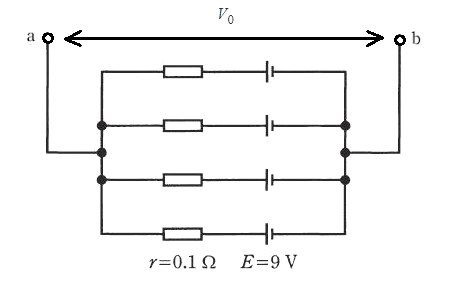
この回路には、電位差がないので電流は流れません。つまり、電源電圧 $E=9$[V]が、端子 ab 間の電圧になります。$V_0=9$[V]
抵抗 $R$ に流れる電流を $I$[A]とすると、テブナンの定理より、
$I=\displaystyle \frac{ V_0 }{ R_0+R }=\displaystyle \frac{ 9 }{ 0.025+0.5 }≒17.14$[A]
抵抗 $R$ で消費される電力を $P$[W]とすると、
$P=RI^2=0.5×17.14^2≒147$[W]
答え (2)
2017年(平成29年)問6【電験理論の過去問題】
$R_1=20Ω$,$R_2=30Ω$ の抵抗、インダクタンス $L_1=20mH$,$L_2=40mH$ のコイル及び静電容量 $C_1=400µF$,$C_2=600µF$ のコンデンサからなる図のような直並列回路がある。直流電圧 $E=100V$ を加えたとき、定常状態において $L_1$,$L_2$,$C_1$ 及び $C_2$ に蓄えられるエネルギーの総和の値[J]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
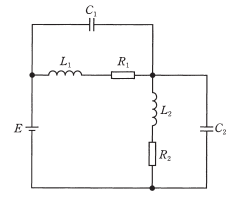
(1) 0.12 (2) 1.20 (3) 1.32 (4) 1.40 (5) 1.52
定常状態中にある直流回路では、コンデンサは開放,コイルは短絡として扱うことが出来ますので、抵抗のみの回路として電流を計算することが出来ます。つまり、定常状態の回路は次の図のように考えることができ、回路に流れる電流 $I$[A]は $2$[A]と計算することができます。
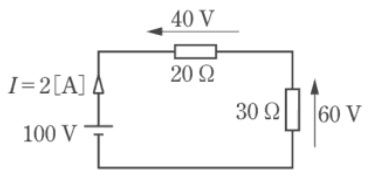
問題文の回路図で考えると、コイル $L_1$,$L_2$ に流れる電流は $2$[A]、各コンデンサ $C_1$,$C_2$ の端子電圧をそれぞれ $V_1$,$V_2$ とすると、並列に接続されている抵抗の端子電圧と等しくなりますので、$V_1=40$[V],$V_2=60$[V]となります。
したがって、コイルとコンデンサ $L_1$,$L_2$,$C_1$,$C_2$ に蓄えられるエネルギー $W_{L1}$,$W_{L2}$,$W_{C1}$,$W_{C2}$ は、
$W_{L1}=\displaystyle\frac{L_1I^2}{2}=\displaystyle\frac{20×10^{-3}×2^2}{2}=0.04$[J]
$W_{L2}=\displaystyle\frac{L_2I^2}{2}=\displaystyle\frac{40×10^{-3}×2^2}{2}=0.08$[J]
$W_{C1}=\displaystyle\frac{C_1{V_1}^2}{2}=\displaystyle\frac{400×10^{-6}×40^2}{2}=0.32$[J]
$W_{C2}=\displaystyle\frac{C_2{V_2}^2}{2}=\displaystyle\frac{600×10^{-6}×60^2}{2}=1.08$[J]
エネルギーの総和 $W$[J]は、
$W=W_{L1}+W_{L2}+W_{C1}+W_{C2}=1.52$[J]
答え(5)
電験三種の理論科目に出題される「直流分野」のページ
1.直流回路の基本問題
2.ホイートストンブリッジ回路
3.キルヒホッフの法則と不平衡ブリッジ回路
4.回路計算の定理(重ね合わせ・テブナン)
5.直流回路の消費電力






