このページでは、単相3線式や三相4線式などの配電理論について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の電力科目の試験で、実際に出題された単相3線式や三相4線式などの配電理論の過去問題も解説しています。
- 配電系統の電気方式
- 電験三種-電力(送配電)過去問題
- 1997年(平成9年)問12
- 1997年(平成9年)問12 過去問解説
- 1998年(平成10年)問9
- 1998年(平成10年)問9 過去問解説
- 2003年(平成15年)問13
- 2003年(平成15年)問13 過去問解説
- 2004年(平成16年)問17
- 2004年(平成16年)問17 過去問解説
- 2005年(平成17年)問7
- 2005年(平成17年)問7 過去問解説
- 2007年(平成19年)問16
- 2007年(平成19年)問16 過去問解説
- 2007年(平成19年)問17
- 2007年(平成19年)問17 過去問解説
- 2009年(平成21年)問12
- 2009年(平成21年)問12 過去問解説
- 2011年(平成23年)問9
- 2011年(平成23年)問9 過去問解説
- 2014年(平成26年)問12
- 2014年(平成26年)問12 過去問解説
- 2014年(平成26年)問16
- 2014年(平成26年)問16 過去問解説
- 2015年(平成27年)問13
- 2015年(平成27年)問13 過去問解説
- 2016年(平成28年)問17
- 2016年(平成28年)問17 過去問解説
配電系統の電気方式
単相2線式配電方式
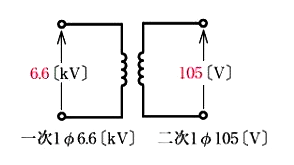
主に小規模の低圧配電に使用されます。往復2線で単相電圧 100 や 200[V]を供給する方式で、電灯および小形動力回路に採用されます。
高低圧混触時に低圧側の対地電圧上昇を抑制するため、低圧側の1線を変圧器端子部分で直接接地(B種接地工事)します。
この方式では1種類の電圧しか得られないことと、100[V]系では電圧降下、線路損失が大きくなるので、小規模の電灯、コンセント回路のほかには用いられません。
単相3線式配電方式

二次低圧側の中性点を直接接地(B種接地工事)して、両外線および中性線の3線を引き出し、外線~中性線間で単相100[V]、両外線間で単相200[V]を供給する電気方式です。
この方式では、2種類の電圧が得られることと、単相100[V]負荷が平衡していれば、中性線電流は相殺して零となり、単相2線式に比べ、電圧降下、線路損失の面で有利となります。反面、二次側配線のこう長が長いか、線が細くて電気抵抗が比較的大きい場合には、負荷が不平衡であれば、負荷電圧が不平衡になる欠点があります。
この方式で中性線が断線すれば、負荷電圧が極端に不平衡になり機器を損傷するおそれがあるため、電気設備技術基準の解釈第39条に、「多線式電路の中性線には過電流遮断器を施設してはならない」としています。
バランサ
単相3線式配電方式において、不平衡負荷による負荷電圧の不平衡を改善するために負荷端近くに設けられる一種の変圧器を「バランサ」といいます。構造的には単3変圧器の一次巻線を除いた巻数比1:1の単巻変圧器と考えられます。負荷が不平衡であればバランサ巻線に負荷電圧を等しくするように電流が流れます。バランサの設置により、負荷電圧が平衡すると同時に配線損失が少なくなる利点もります。
バランサがない場合の例
次の回路の中性線には10[A]の電流が流れています。AB間の電圧 VAB[V]及びBC間の電圧 VBC[V]、線路損失 PL[W]を求めてみます。
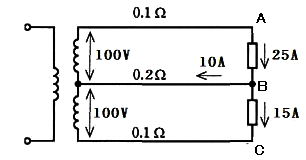
100=0.1×25+VAB+0.2×10
VAB=95.5[V]
100=-0.2×10+VBC+0.1×15
VBC=100.5[V]
PL=0.1×252+0.2×102+0.1×152=105[W]
バランサがある場合の例
次の回路のようにバランサを設置すると、中性線に流れる電流がバランサ側に流れます。AB間の電圧 VAB[V]及びBC間の電圧 VBC[V]、線路損失 PL[W]を求めてみます。
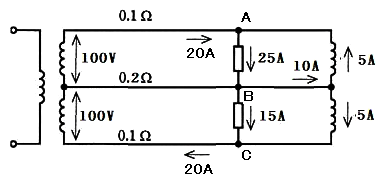
100=0.1×20+VAB
VAB=98[V]
100=VBC+0.1×20
VBC=98[V]
PL=2×0.1×202=80[W]
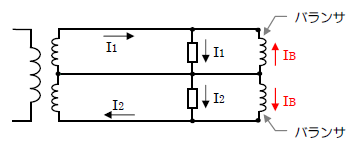
バランサに流れる電流を求める式
$I_B=\displaystyle \frac{I_1-I_2}{2}$
$I_B$:バランサに流れる電流
$I_1$:負荷1 に流れる電流
$I_2$:負荷2 に流れる電流
三相3線式配電方式
3線に対称三相交流電圧をかけて送電する電気方式です。低圧配電では比較的容量の大きい動力負荷にはこの方式で給電することが多いです。低圧三相3線式配電の公称電圧は 200 または 415[V]であり、変圧器二次側の結線は△またはYあるいはV結線が採用されます。尚、中性点または低圧側の1端子を直接接地(B種接地工事)します。
平衡三相交流の瞬時電力は、電圧、電流、力率が一定であれば、原理的に、時間的に一定(すなわち脈動がない)であり、回転機(発電機、電動機など)にとって都合がよいことが、この方式が多く採用される理由です。
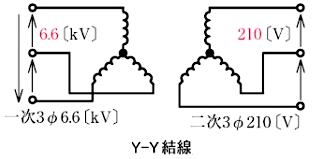
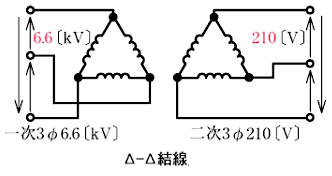
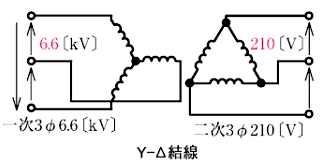
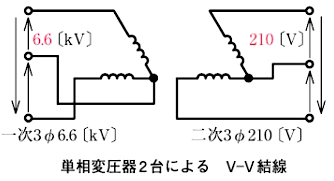
三相4線式配電方式
変圧器の中性点から1線(中性線)を引き出し、電圧線の3線と中性線との4線で送電する方式です。低圧三相4線式では、公称電圧 240/415[V](負荷の定格電圧は 230/400[V])とされており、単相負荷と三相負荷が混在する場合には適当な方式といえます。
![400[V]級三相4線式](https://e-sysnet.com/wp-content/uploads/2025/04/image-18.png)
400V配電は、工場や大形ビルなどの動力負荷の大きい所に採用されています。三相3線式に比べ電流が小さくなり、配線が細くてすむので配線費を節約できます。また同一配線を使用した場合には、電圧降下、線路損失の面で有利となります。この方式の分岐回路は、電灯用には230[V]で、動力用には三相400[V]で供給するのが普通です。また一般の 100[V]回路には 230/100[V]または、400/100[V]の二巻線または単巻の降圧トランスを用いて給電します。
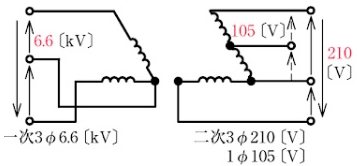
低圧三相4線式配電には、異容量V結線(灯動共用4線式などともいう)という配電方式があります。この方式では 100/200[V]の単相3線式の部分で単相負荷に給電し、200[V]三相3線式の部分で三相200[V]負荷に給電します。この場合、通常、共用変圧器の方の容量を大きくするので、「異容量」と呼ばれています。
異容量V結線の電圧ベクトルと対地電圧の例
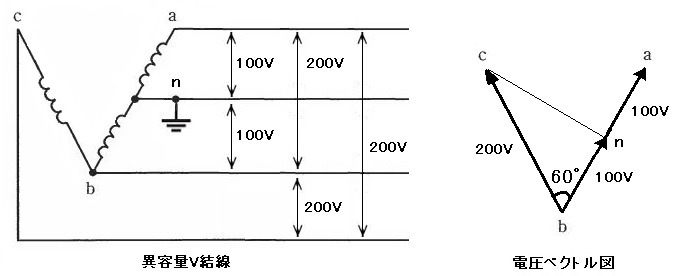
a,b,c間の各線間電圧は 200[V]ですが、単相3線式部分のn点は通常は接地します。a,b点の対地電圧は 100[V]となります。c点の対地電圧 Ec[V]は cn の長さになりますので、
$E_c=200×sin60°=100\sqrt{3 }$[V]
になります。
異容量V結線の進み接続
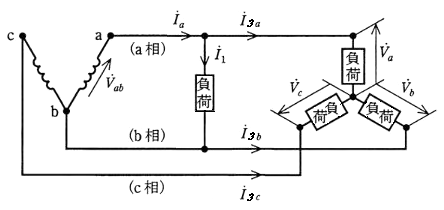
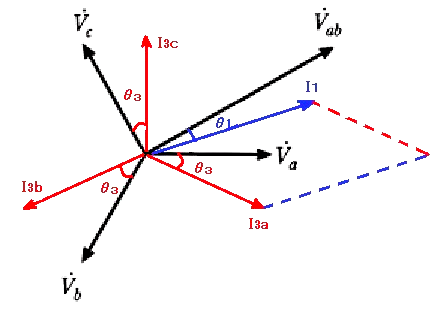
相回転を a,b,c とした場合、ab間に単相負荷を接続する方式を「進み接続」といいます。単相負荷の力率角を θ1(遅れ)とすると、単相負荷の電流 $\vec{ I_1}$ は、ab間の線間電圧 $\vec{ V_{ab}}$ より、θ1 遅れた方向になります。
三相負荷の力率角を θ3(遅れ)とすると、各相の負荷電流 $\vec{ I_{3a}}$,$\vec{ I_{3b}}$,$\vec{ I_{3c}}$ は相電圧 $\vec{ V_{a}}$,$\vec{ V_{b}}$,$\vec{ V_{c}}$ より、おのおの θ3 遅れた方向になります。
ab間に流れる電流は、
$\vec{ I_a}=\vec{ I_1}+\vec{ I_{3a}}$
となり、ベクトルを合成して求めることができます。
異容量V結線の遅れ接続
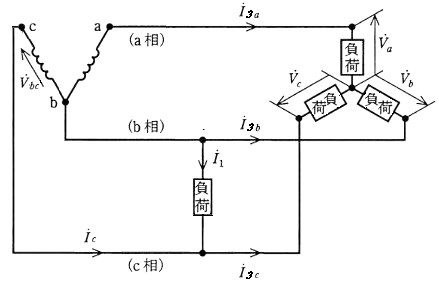
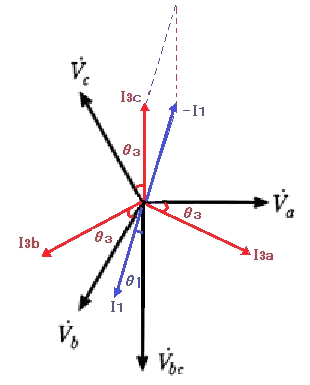
相回転を a,b,c とした場合、bc間に単相負荷を接続する方式を「遅れ接続」といいます。単相負荷の力率角を θ1(遅れ)とすると、単相負荷の電流 $\vec{ I_1}$ は、bc間の線間電圧 $\vec{ V_{bc}}$ より、θ1 遅れた方向になります。
三相負荷の力率角を θ3(遅れ)とすると、各相の負荷電流 $\vec{ I_{3a}}$,$\vec{ I_{3b}}$,$\vec{ I_{3c}}$ は相電圧 $\vec{ V_{a}}$,$\vec{ V_{b}}$,$\vec{ V_{c}}$ より、おのおの θ3 遅れた方向になります。
bc間に流れる電流は、
$\vec{ I_c}=-\vec{ I_1}+\vec{ I_{3c}}$
となり、ベクトルを合成して求めることができます。
電験三種-電力(送配電)過去問題
1997年(平成9年)問12
図のように三相3線式負荷を接続する配電系統がある。各部の電圧が図のとおりであるとき、変圧器の一次側の線電流 I[A]は、次のうちどれか。
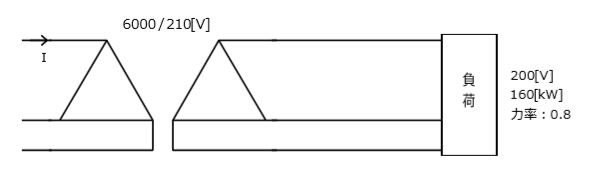
(1) 16.5 (2) 20.2 (3) 27.7 (4) 28.3 (5) 34.6
1997年(平成9年)問12 過去問解説
負荷の皮相電力を S[V・A]とすると、
S=160/0.8=200[kV・A]
変圧器の1次側電圧を V[V]とすると、
V=6000×200/210=5714[V]
1次側電圧が V=5714[V]のときに、皮相電力が S=200[kV・A]になる線電流 I[A]は、
S=$\sqrt{3 }$VI
200×103= $\sqrt{3 }$×5714×I
I≒20.2[A]
答え (2)
1998年(平成10年)問9
規模の大きいビルなどの屋内配線に400[V]配線方式の採用が増加しつつある。この配電方式は受電用変圧器の二次側を( ア )結線し、中性点を直接接地した( イ )で構成される。用途としては、電動機などの動力負荷は電圧線間に接続し、( ウ )などの照明負荷は中性線と電圧線との間に接続し、電灯・動力設備の共用、電圧格上げによる供給量の増加を図ったものである。なお、( エ )、コンセント回路などは変圧器を介し100[V]で供給する。
上記の記述中の空白の(ア),(イ),(ウ)及び(エ)に記入する記号又は字句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | Y | 三相4線式 | 蛍光灯及び水銀灯 | 白熱電灯 |
| (2) | Y | 三相3線式 | 白熱電灯 | 蛍光灯及び水銀灯 |
| (3) | Y | 三相4線式 | 白熱電灯 | 蛍光灯及び水銀灯 |
| (4) | △ | 三相3線式 | 白熱電灯 | 蛍光灯及び水銀灯 |
| (5) | △ | 三相3線式 | 蛍光灯及び水銀灯 | 白熱電灯 |
1998年(平成10年)問9 過去問解説
規模の大きいビルなどの屋内配線に400[V]配線方式の採用が増加しつつある。この配電方式は受電用変圧器の二次側を( Y )結線し、中性点を直接接地した( 三相4線式 )で構成される。用途としては、電動機などの動力負荷は電圧線間に接続し、( 蛍光灯及び水銀灯 )などの照明負荷は中性線と電圧線との間に接続し、電灯・動力設備の共用、電圧格上げによる供給量の増加を図ったものである。なお、( 白熱電灯 )、コンセント回路などは変圧器を介し100[V]で供給する。
答え (1)
2003年(平成15年)問13
100/200[V]単相3線式配電方式に関する記述として、誤っているものは次のうちどれか。
- 中性線が断線すると、異常電圧を発生する。
- 負荷の分布によっては、負荷電圧が不平衡になることがある。
- 配電容量が等しい場合、100[V]単相2線式配電方式より電線の銅量が少なくてすむ。
- バランサは、電源の近くに設ける方が効果的である。
- 単相200[V]負荷の使用が可能である。
2003年(平成15年)問13 過去問解説
バランサは各配線の電流のバランスを補償するために用いるもので、負荷端近くに設置します。
答え (4)
2004年(平成16年)問17
図のように、電圧線及び中性線の抵抗がそれぞれ 0.1[Ω]及び 0.2[Ω]の 100/200[V]単相3線式配電線に、力率が 100[%]で電流がそれぞれ 60[A]及び 40[A]の二つの負荷が接続されている。
この配電線路にバランサを接続した場合について、次の(a)及び(b)に答えよ。
ただし、負荷電流は一定とし、線路抵抗以外のインピーダンスは無視するものとする。
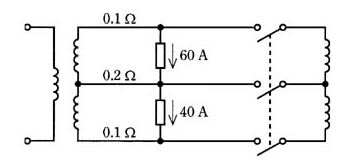
(a) バランサに流れる電流[A]の値として、正しいのは次のうちどれか。
(1)5 (2)7 (3)10 (4)15 (5)20
(b) バランサを接続したことによる線路損失の減少量[W]の値として、正しいは次のうちどれか。
(1)50 (2)75 (3)85 (4)100 (5)110
2004年(平成16年)問17 過去問解説
(a) バランサを接続したときの、電流の分布を図に示します。
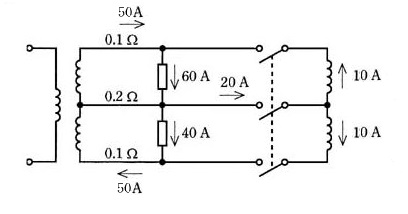
それぞれのバランサに流れる電流は 10[A]になります。
答え (3)
(b) バランサを接続したときの線路損失を PL とすると、
PL = 2I2r = 2×502×0.1=500 [W]
バランサがない場合の線路損失をPL‘ とすると、
PL‘ = Ia2r+Ib2r+Ic2r
=602×0.1+202×0.2+402×0.1
=600 [W]
PL‘-PL = 600-500 =100[W]
答え (4)
2005年(平成17年)問7
送配電方式として広く採用されている交流三相方式に関する記述として、誤っているのは次のうちどれか。
- 三相回路が平衡している場合、三相交流全体の瞬時電力は時間に無関係な一定値となり、単相交流の場合のように脈動しないという利点がある。
- 同一材料の電線を使用して、同じ線間電圧で同じ電力を同じ距離に、同じ損失で送電する場合に必要な電線の総重量は、三相3線式でも単相2線式と同等である。
- 電源側をY結線としたうえで、中性線を施設して三相4線式とすると、線間電圧と相電圧の両方を容易に取り出して利用できるようになる。
- 発電機では、同じ出力ならば、単相の場合に比べるとより小形に設計できて効率がよい。
- 回転磁界が容易に得られるため、動力源として三相誘導電動機の活用に便利である。
2005年(平成17年)問7 過去問解説
同一材料の電線を使用して、同じ線間電圧で同じ電力を同じ距離に、同じ損失で送電する場合、三相送電方式の方が電線銅重量が少なくなります。
答え (2)
2007年(平成19年)問16
2台の単相変圧器(容量 75[kVA]の T1 及び 50[kVA]の T2 )をV結線に接続し、下図のように三相平衡負荷 45[kW](力率角 進み π/6[rad])と単相負荷 P(力率=1)に電力を供給している。これについて、次の(a)及び(b)に答えよ。
ただし、相順はa,b,cとし、図示していないインピーダンスは無視するものとする。
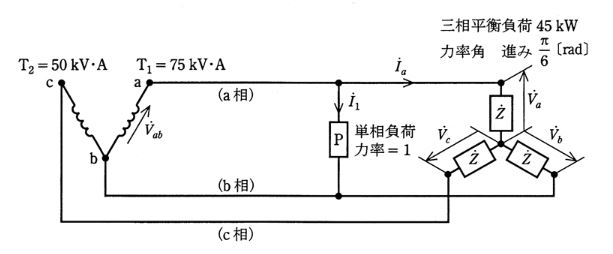
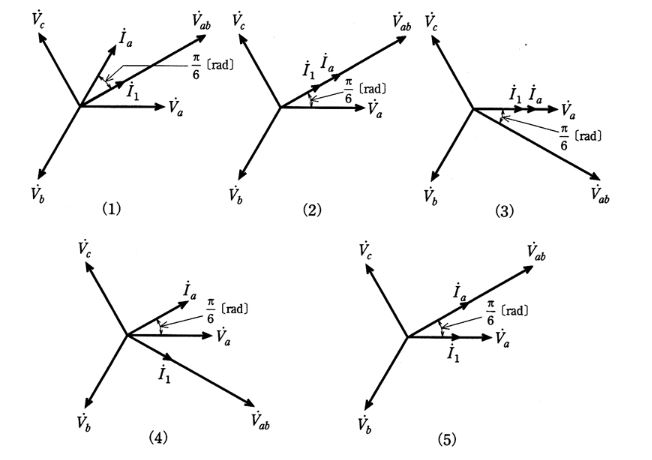
(a) 問題の図において、$\dot{ V} _a $ を基準とし、$\dot{ V }_{ab} $,$\dot{ I } _a$,$\dot{ I } _1$ の大きさと位相関係を示す図として、正しいのは次のうちどれか。
ただし、$| \dot{ I } _a |>|\dot{ I}_1|$ とする。
(b) 単相変圧器 T1 が過負荷にならない範囲で、単相負荷 P(力率=1)がとりうる最大電力[kW]の値として、正しいのは次のうちどれか。
(1)23 (2)36 (3)45 (4)49 (5)58
2007年(平成19年)問16 過去問解説
(a) $\dot{ I } _a$ は $\dot{ V }_a$ より、π/6[rad]進んだベクトルになります。また、$\dot{ I } _1$ は $\dot{ V }_{ab} $ と同じ向きになります。ベクトル図は(2)になります。
答え (2)
(b) 三相平衡負荷の消費電力 P[W]は、
$P=\sqrt{3 }×線間電圧×線電流×力率$
$45 = \sqrt{3 }×V_{ab}×I_a×\displaystyle \frac{ \sqrt{3 } }{ 2 }$
$I_a = \displaystyle \frac{ 30 }{ V_{ab} }$[A]
単相変圧器 T1 に流すことができる電流は $\displaystyle \frac{ 75}{ V_{ab} }$[A]ですので、$I_1 $[A]は、
$I_1= \displaystyle \frac{ 75}{ V_{ab} }-I_a=\displaystyle \frac{ 45}{ V_{ab} }$
単相負荷 P[kW]は、
$P=V_{ab}×I_1=V_{ab}×\displaystyle \frac{ 45}{ V_{ab} }=45$ [kW]
答え (3)
2007年(平成19年)問17
図のような単相3線式配電線路がある。系統の中間点に図の通り負荷が接続されており、端末のAC間に太陽光発電設備が逆変換装置を介して接続されている。各部の電圧及び電流が図に示された値であるとき、次の(a)及び(b)に答えよ。
ただし、図示していないインピーダンスは無視するとともに、線路のインピーダンスは抵抗であり、負荷の力率は 1、太陽光発電設備は発電出力電流(交流側) 15[A]、力率 1で一定とする。
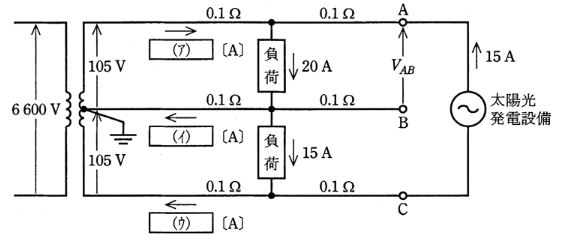
(a) 図中の回路の空白箇所(ア),(イ)及び(ウ)に流れる電流[A]の値として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | 5 | 0 | 15 |
| (2) | 5 | 5 | 0 |
| (3) | 15 | 0 | 15 |
| (4) | 20 | 5 | 0 |
| (5) | 20 | 5 | 15 |
(b) 図中AB間の端子電圧 VAB の値として、正しいのは次のうちどれか。
(1) 104.0 (2) 104.5 (3) 105.0 (4) 105.5 (5) 106.0
2007年(平成19年)問17 過去問解説
(a) キルヒホッフの第1法則を適用します。
I(ア)+15=20 ∴I(ア)=5
20=I(イ)+15 ∴I(イ)=5
15=I(ウ)+15 ∴I(ウ)=0
答え (2)
(b) 回路図を示します。
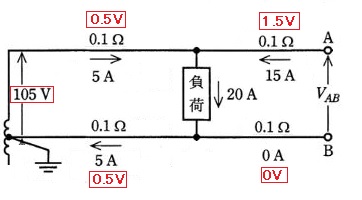
外周にキルヒホッフの第2法則を適用します。
105=0.5-1.5+VAB+0+0.5[V]
VAB=105.5[V]
答え (4)
2009年(平成21年)問12
配電で使われる変圧器に関する記述として、誤っているのは次のうちどれか。下図を参考にして答えよ。
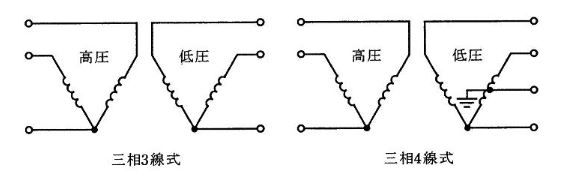
- 柱上に設置される変圧器の容量は、50[kV・A]以下の比較的小型のものが多い。
- 柱上に設置される三相3線式の変圧器は、一般的に同一容量の単相変圧器のV結線を採用しており、出力はΔ結線の $\displaystyle \frac{ 1 }{ \sqrt{ 3 } }$ 倍となる。また、V結線変圧器の利用率は $\displaystyle \frac{ \sqrt{ 3 } }{ 2 }$ となる。
- 三相4線式(V結線)の変圧器容量の選定は、単相と三相の負荷割合やその負荷曲線及び電力損失を考慮して決定するので、同一容量の単相変圧器を組み合わせることが多い。
- 配電線路の運用状況や設備実態を把握するため、変圧器二次側の電圧、電流及び接地抵抗の測定を実施している。
- 地上配置形の変圧器は、開閉器、保護装置を内蔵し金属製のケースに収めたもので、地中配電線供給エリアで使用される。
2009年(平成21年)問12 過去問解説
三相4線式(V結線)の変圧器容量の選定は、単相と三相の負荷割合やその負荷曲線及び電力損失を考慮して決定します。通常は共用変圧器の方の容量を大きくします。
答え (3)
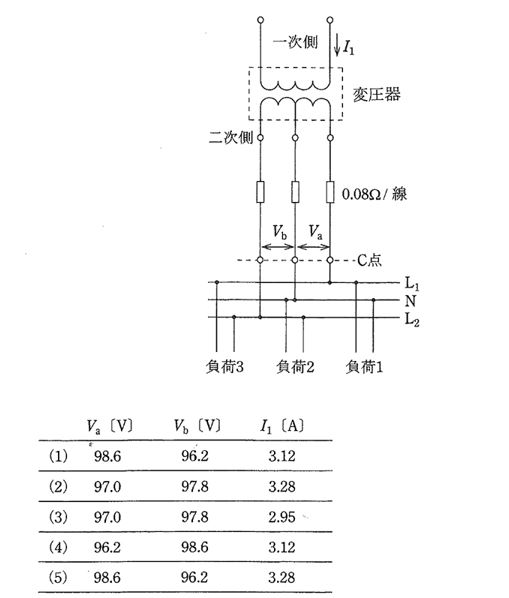
2011年(平成23年)問9
一次電圧 6400[V]、二次電圧 210[V]/105[V]の柱上変圧器がある。図のような単相3線式配電線路において三つの無誘導負荷が接続されている。負荷1の電流は 50[A]、負荷2の電流は 60[A]、負荷3の電流は 40[A]である。L1 と N 間の電圧 Va[V]、L2 と N間の電圧 Vb[V]、及び変圧器の一次電流 I1[A]の値の組合せとして正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,変圧器から低圧負荷までの電線1線当たりの抵抗を 0.08[Ω]とし、変圧器の励磁電流、インピーダンス、低圧配電線のリアクタンス、及び C点から負荷側線路のインピーダンスは考えないものとする。
2011年(平成23年)問9 過去問解説
問題文を図示すると次のようになります。
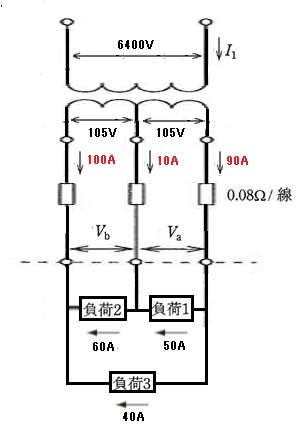
キルヒホッフの第2法則を適用します。
Va=105-90×0.08+10×0.08=98.6[V]
Vb=105-10×0.08-100×0.08=96.2[V]
一次側と二次側の容量は等しくなりますので、
6400×I1=105×90+105×100
$I_1=3.12$[A]
答え (1)
2014年(平成26年)問12
図のように、2台の単相変圧器による電灯動力共用の三相4線式低圧配電線に、平衡三相負荷 45kW(遅れ力率角30°)1個及び単相負荷 10kW(力率=1)2個が接続されている。これに供給するための共用変圧器及び専用変圧器の容量の値[kV・A]は、それぞれいくら以上でなければならないか。値の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、相回転はa’‐c’‐b’とする。
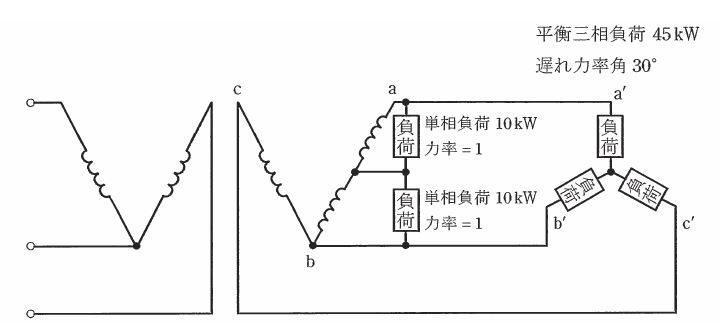
| 共用変圧器の容量 | 専用変圧器の容量 | |
| (1) | 20 | 30 |
| (2) | 30 | 20 |
| (3) | 40 | 20 |
| (4) | 20 | 40 |
| (5) | 50 | 30 |
2014年(平成26年)問12 過去問解説
単相負荷は平衡しているので、各単相負荷に流れる電流を I1[A]とすると、
$P=2×I_1×\displaystyle \frac{ V_{ab} }{ 2 }$
$10×10^3+10×10^3=2×I_1×\displaystyle \frac{ V_{ab} }{ 2 }$
$I_1=\displaystyle \frac{ 20×10^3 }{ V_{ab} }$[A]
三相負荷に流れる電流を I3[A]とすると、
$P=\sqrt{ 3 }V_{ab} I_3cosθ$
$45×10^3=\sqrt{ 3 }V_{ab} I_3×\displaystyle \frac{ \sqrt{ 3 } }{ 2 }$
$I_3=\displaystyle \frac{ 30×10^3 }{ V_{ab} }$[A]
共用変圧器の容量 Pab[W]及び、専用変圧器の容量 Pbc[W]は、
$\begin{eqnarray}P_{ab} &=& V_{ab} ×(I_1+I_3) \\\\&=& V_{ab} ×\left(\displaystyle \frac{ 20×10^3 }{ V_{ab} }+\displaystyle \frac{ 30×10^3 }{ V_{ab} }\right)\\\\&=&50×10^3[W]\end{eqnarray}$
$\begin{eqnarray}P_{bc} &=& V_{bc} ×I_3 \\\\&=& V_{ab} ×I_3\\\\&=&V_{ab} ×\displaystyle \frac{ 30×10^3 }{ V_{ab} }\\\\&=&30×10^3[W]\end{eqnarray}$
答え (5)
2014年(平成26年)問16
図に示すように、中性点をリアクトルLを介して接地している公称電圧 66kV の系統があるとき、次の(a)及び(b)の問に答えよ。
なお、図中のCは、送電線の対地静電容量に相当する等価キャパシタを示す。また、図に表示されていない電気定数は無視する。
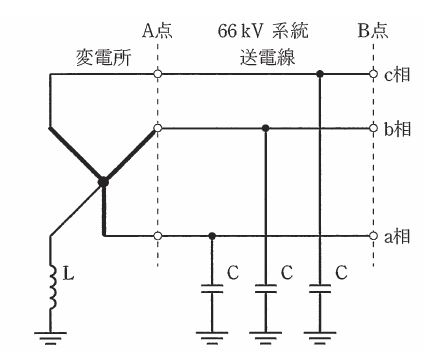
(a) 送電線の線路定数を測定するために、図中のA点で変電所と送電線を切り離し、A点で送電線の3線を一括して、これと大地間に公称電圧の相電圧相当の電圧を加えて充電すると、一括した線に流れる全充電電流は 115A であった。このとき、この送電線の1相当たりのアドミタンスの大きさ[mS]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.58 (2) 1.0 (3) 1.7 (4) 3.0 (5) 9.1
(b) 図中のB点のa相で1線地絡事故が発生したとき、地絡点を流れる電流を零とするために必要なリアクトルLのインピーダンスの大きさ[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、送電線の電気定数は、(a)で求めた値を用いるものとする。
(1) 111 (2) 196 (3) 333 (4) 575 (5) 1000
2014年(平成26年)問16 過去問解説
(A) アドミタンス Y(単位[S]:ジーメンス)は、インピーダンス Z [Ω] の逆数です。電流 I[A]と電圧 E[V]との関係は、
$I=\displaystyle \frac{ E}{ Z }=EY$[A]
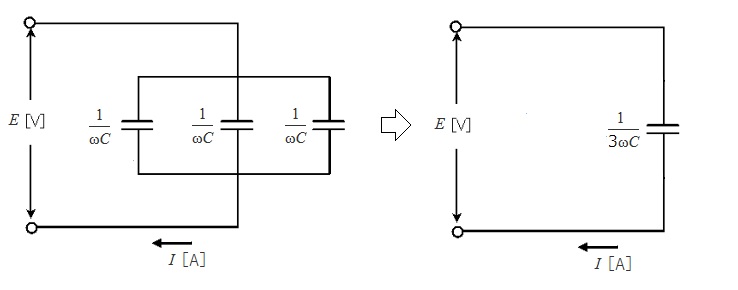
A点で送電線の3線を一括して、これと大地間に公称電圧の相電圧相当の電圧を加えて充電したときの等価回路を示します。 リアクタンスを $\displaystyle \frac{ 1}{ ωC }=X_C$ とすれば、等価回路図より
$X_C=\displaystyle \frac{3E }{ I }=\displaystyle \frac{3×\displaystyle \frac{66000 }{ \sqrt{3} } }{ 115 }=994$[Ω]
$Y=\displaystyle \frac{1 }{ X_C }=\displaystyle \frac{1 }{ 994 }=0.001$[S]
答え (2)
(b) 地絡点を流れる電流を零とするには、容量性リアクタンスと誘導性リアクタンスの大きさが等しくなれば良いということです。つまり、並列共振が起これば良いということです。
$X_L=\displaystyle \frac{X_C }{ 3 }=\displaystyle \frac{1 }{ 3Y }=333$[Ω]
答え (3)
2015年(平成27年)問13
三相3線式と単相2線式の低圧配電方式について、三相3線式の最大送電電力は、単相2線式のおよそ何%となるか。最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、三相3線式の負荷は平衡しており、両低圧配電方式の線路こう長、低圧配電線に用いられる導体材料や導体量、送電端の線間電圧、力率は等しく、許容電流は導体の断面積に比例するものとする。
(1) 67 (2) 115 (3) 133 (4) 173 (5) 260
2015年(平成27年)問13 過去問解説
両低圧配電方式の線路こう長を L[m]、単相2線式の断面積を S2[m2]、三相3線式の断面積を S3[m2]とすると、
$2×S_2×L=3×S_3×L$
$2S_2=3S_3$
許容電流は導体の断面積に比例するので,単相2線式の許容電流を I2[A]、三相3線式の許容電流を I3[A]とすると、
$2S_2=3S_3$ ⇒ $2I_2=3I_3$
単相2線式の最大送電電力を P2、三相3線式の最大送電電力を P3 とすると、
$P_2=VI_2cosθ$
$P_3=\sqrt{ 3 }VI_3cosθ$
$\begin{eqnarray}\displaystyle \frac{ P_3}{P_2 } &=& \displaystyle \frac{ \sqrt{ 3 }VI_3cosθ}{VI_2cosθ } \\\\&=& \displaystyle \frac{ \sqrt{ 3 }I_3}{I_2 } \\\\&=&\displaystyle \sqrt{ 3 }×\frac{ 2}{3}=1.15\end{eqnarray}$
答え (2)
2016年(平成28年)問17
図のような、線路抵抗をもった 100/200V 単相3線式配電線路に、力率が 100%で電流がそれぞれ 30A及び 20Aの二つの負荷が接続されている。この配電線路にバランサを接続した場合について、次の(a)及び(b)の問に答えよ。
ただし、バランサの接続前後で負荷電流は変化しないものとし、線路抵抗以外のインピーダンスは無視するものとする。

(a) バランサ接続後a’-b’間に流れる電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 5 (2) 10 (3) 20 (4) 25 (5) 30
(b) バランサ接続前後の線路損失の変化量の値[W]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 20 (2) 65 (3) 80 (4) 125 (5) 145
2016年(平成28年)問17 過去問解説
(a) バランサを接続したときの、電流の分布を図に示します。
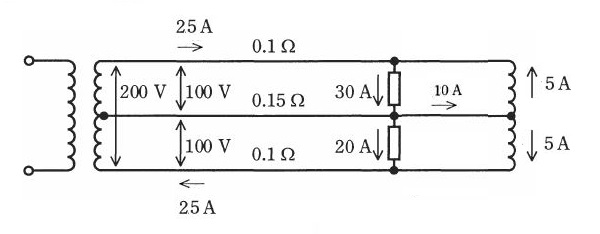
それぞれのバランサに流れる電流は 5[A]になります。
答え (1)
(b) バランサを接続したときの線路損失を PL[W]とすると、
PL = 2I2r = 2×252×0.1=125[W]
バランサがない場合の線路損失を PL‘[W]とすると、
PL‘ = Ia2r+Ib2r+Ic2r
=302×0.1+102×0.15+202×0.1
=145[W]
PL‘-PL = 145-125 =20[W]
答え (1)





