このページでは、線路損失と電圧降下について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の電力科目の試験で、実際に出題された線路損失と電圧降下の過去問題も解説しています。
- 線路損失(抵抗損)
- 電圧降下
- 覚えておきたい必要な公式
- 電験三種-電力(送配電)過去問題
- 1999年(平成11年)問12
- 1999年(平成11年)問12 過去問解説
- 2000年(平成12年)問1
- 2000年(平成12年)問1 過去問解説
- 2000年(平成12年)問10
- 2000年(平成12年)問10 過去問解説
- 2002年(平成14年)問9
- 2002年(平成14年)問9 過去問解説
- 2005年(平成17年)問9
- 2005年(平成17年)問9 過去問解説
- 2006年(平成18年)問16
- 2006年(平成18年)問16 過去問解説
- 2007年(平成19年)問10
- 2007年(平成19年)問10 過去問解説
- 2008年(平成20年)問17
- 2008年(平成20年)問17 過去問解説
- 2009年(平成21年)問10
- 2009年(平成21年)問10 過去問解説
- 2011年(平成23年)問17
- 2011年(平成23年)問17 過去問解説
- 2012年(平成24年)問10
- 2012年(平成24年)問10 過去問解説
- 2012年(平成24年)問16
- 2012年(平成24年)問16 過去問解説
- 2014年(平成26年)問7
- 2014年(平成26年)問7 過去問解説
- 2016年(平成28年)問9
- 2016年(平成28年)問9 過去問解説
- 2017年(平成29年)問11
- 2017年(平成29年)問11 過去問解説
線路損失(抵抗損)
送電線路で電力を送る場合、受電端まで達せず途中でむだに失われる電力を線路損失といいます。線路損失には、抵抗損、コロナ損、漏れ電流損などがあります。このうち抵抗損が代表的であり、線路の抵抗を $r$[Ω]、流れる電流を $I$[A]とすると、1線当たりの線路損失 $P_L$ を求める公式は次のようになります。($P_L$:Lossの”L”)
1線当たりの線路損失を求める公式
$P_L=I^2r$
$P_L$ [W]:線路損失
$I$ [A]:電流
$r$ [Ω]:線路の抵抗
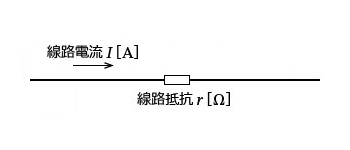
この損失は熱エネルギーとなり、電線温度を上昇させる原因になります。そのため、送電線路では電圧を高くし、電流を小さくして送電するほど低損失で安定に送電できます。
単相2線式の負荷電力と線路損失
送電端の線間電圧を $V_S$[V](supplyの”s”)、受電端の線間電圧を $V_r$[V](receiveの”r”)、線路の抵抗を $r$[Ω]、流れる電流を $I$[A]とすると、負荷電力 $P$ と、線路損失 $P_L$ を求める公式は次のようになります。
単相2線式の負荷電力と線路損失を求める公式
負荷電力:$P=V_rIcosθ$
線路損失:$P_L = 2I^2r = \displaystyle \frac{ 2P^2r }{ (Vrcosθ)^2 } $
$P$ [W]:負荷電力
$P_L$ [W]:線路損失
$V_r$[V]:受電端の線間電圧
$I$ [A]:電流
$r$ [Ω]:線路の抵抗
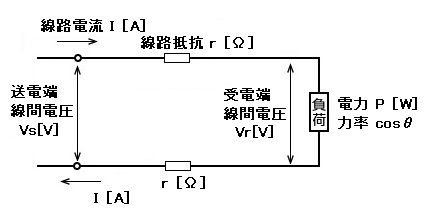
単相2線式では、 電線が2本になるため、1線当たりの線路損失の2倍になります。
単相3線式の負荷電力と線路損失
単相3線式で、負荷が平衡している場合の、負荷電力 $P$ と、線路損失 $P_L$ を求める公式は次のようになります。平衡負荷の場合、中性線に電流が流れませんので電線2本分の電力損失になります。
負荷が平衡している場合の単相3線式の負荷電力と線路損失を求める公式
$P=2V_rIcosθ$
$P_L = 2I^2r = \displaystyle \frac{ P^2r }{ 2(Vrcosθ)^2 } $
$P$ [W]:負荷電力
$P_L$ [W]:線路損失
$V_r$[V]:受電端の線間電圧
$I$ [A]:電流
$r$ [Ω]:線路の抵抗
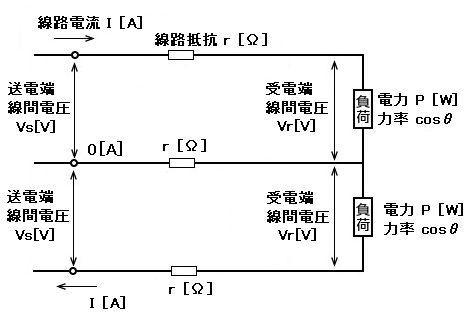
単相3線式で、負荷が不平衡の場合は次のようになります。不平衡負荷の場合、中性線に電流が流れるので電線3本分の電力損失になります。
負荷が不平衡の場合の単相3線式の負荷電力と線路損失を求める公式
$P=P_1+P_2$
$P_1=Vr_1(I_a-I_c)cosθ_1$
$P_2=Vr_2(I_b-I_c)cosθ_2$
$P_L = I_a^2r+I_b^2r+I_c^2r$
$P$ [W]:負荷電力
$P_L$ [W]:線路損失
$V_r$[V]:受電端の線間電圧
$I$ [A]:電流
$r$ [Ω]:線路の抵抗
$I_c$は流れる向きによって、符号が変わります。
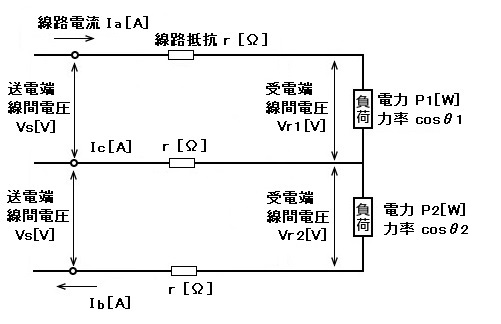
三相3線式の負荷電力と線路損失
三相3線式の負荷電力 $P$ と、線路損失 $P_L$ を求める公式は次のようになります。
三相3線式の負荷電力と線路損失を求める公式
$P=\sqrt{ 3 }V_rIcosθ$
$P_L = 3I^2r = \displaystyle \frac{ P^2r }{ (Vrcosθ)^2 } $
$P$ [W]:負荷電力
$P_L$ [W]:線路損失
$V_r$[V]:受電端の線間電圧
$I$ [A]:電流
$r$ [Ω]:線路の抵抗

三相3線式では、電線3本分の電力損失になります。
電圧降下
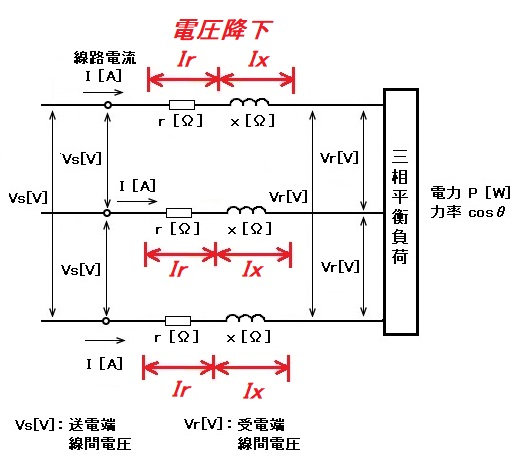
交流回路の送電端線間電圧を Vs、受電端線間電圧を Vr、電線1線分の抵抗を r、電線1線分のリアクタンスを x、負荷の力率を cosθ としたとき、1線分電圧降下の等価回路とベクトル図は次のようになります。
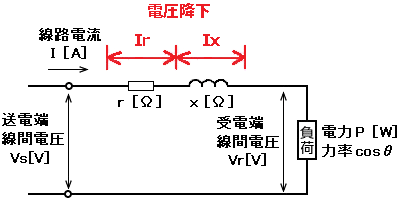
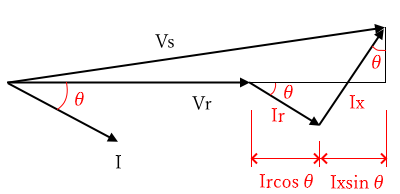
1線分電圧降下のベクトル図より送電端線間電圧 Vs の近似値は次の式で求めることができます。
$Vs≒Vr+I(rcosθ+xsinθ)$(近似式)
電線1線分の電圧降下 VL は次の式で求めることができます。
1線分の電圧降下の定義式
$V_L=V_s-V_r$
1線分の電圧降下の近似式
$V_L≒I(rcosθ+xsinθ)$
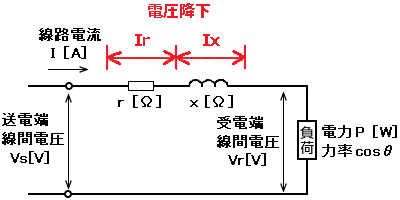
単相2線式の線路電圧降下の公式
送電端線間電圧
$Vs≒Vr+2I(rcosθ+xsinθ)$
電圧降下の定義式
$V_L=Vs-Vr$
電圧降下の近似式
$V_L≒2I(rcosθ+xsinθ)$

単相3線式の線路電圧降下の公式
負荷が平衡している場合
送電端線間電圧
$Vs≒Vr+I(rcosθ+xsinθ)$
電圧降下の定義式
$V_L=Vs-Vr$
電圧降下の近似式
$V_L≒I(rcosθ+xsinθ)$
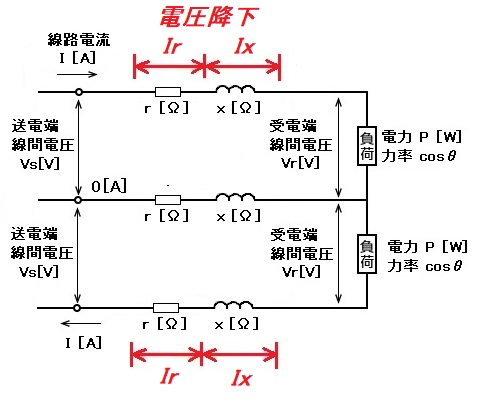
負荷が不平衡の場合


図のように単相2線式の回路が2つあるものと考え、各種法則や定理を用いて導きます。
三相3線式の線路電圧降下の公式
送電端線間電圧
$Vs≒Vr+\sqrt{ 3 }I(rcosθ+xsinθ)$
電圧降下の定義式
$V_L=Vs-Vr$
電圧降下の近似式
$V_L≒\sqrt{ 3 }I(rcosθ+xsinθ)$
覚えておきたい必要な公式
電圧降下率
配線中に発生する電圧降下(絶対値)の受電電圧(絶対値)に対する割合を電圧降下率といいます。電圧降下率 εは、送電端電圧を Vs、受電端電圧を Vr、電圧降下を VL とすると、次の式で求めることができます。
電圧降下率を求める式
$ε=\displaystyle \frac{ V_L }{ Vr }×100=\displaystyle \frac{ Vs-Vr }{ Vr }×100$[%]
$ε$:電圧降下率
$Vs$:送電端電圧
$Vr$:受電端電圧
$V_L$:電圧降下を
抵抗率ρと抵抗値Rの関係式
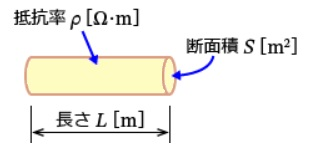
抵抗の値は、導体種類、形状、温度によって異なる値となります。1辺が1[m]の立方体の導体の、相対する2面間の抵抗を、その導体の抵抗率 ρ[Ω⋅m]といい、長さ L[m]、断面積 S[m2]の導体の抵抗値 R[Ω]は次の式で求めることができます。
抵抗率 $ρ$ と抵抗値 $R$ の関係式
$R=ρ\displaystyle \frac{ L }{ S }$[Ω]
$ρ$[Ω⋅m]:抵抗率
$L$[m]:長さ
$S$[m2]:断面積
$R$[Ω]:導体の抵抗値
変圧器の定格容量
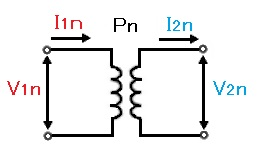
定格二次電圧、定格周波数、力率100%の時の二次端子間の電力を定格容量といい、単位は「V・A]や [kV・A]を使います。定格容量と電圧、電流の関係を次の式で表すことができます。
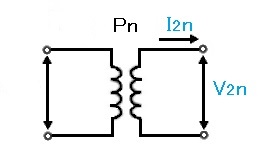
Pn = V2n × I2n[V・A]
Pn:定格容量
V2n:定格二次電圧
I2n:定格二次電流
また、$V_1 I_1 = V_2I_2$であるため、次の関係式も成り立ちます。
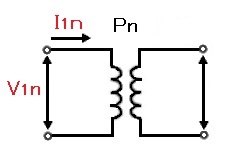
Pn = V1n × I1n[V・A]
Pn:定格容量
V1n:定格一次電圧
I1n:定格一次電流
上記の関係より、次の式が成り立ちます。
定格容量と電圧、電流の関係式
Pn = V1n × I1n = V2n × I2n
Pn:定格容量
V1n:定格一次電圧
I1n:定格一次電流
V2n:定格二次電圧
I2n:定格二次電流
三相変圧器の定格容量を求める式
Pn = √3 Vn × In
Pn:定格容量
Vn:定格電圧
In:定格電流
電験三種-電力(送配電)過去問題
1999年(平成11年)問12
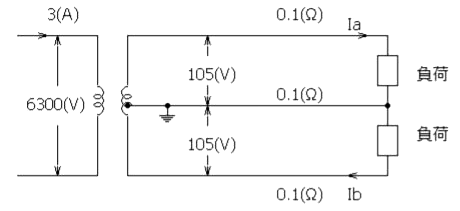
図のような単相 3 線式の低圧配電線路において、負荷電流 Ia と Ib の比が 1:2 である場合の二次側線路損失[kW]の値として、正しいのは次のうちどれか。 ただし、変圧器の一次電圧は 6300[V]、一次電流は 3[A]、二次電圧は 105/210[V]、 電線 1 線当たりの抵抗は 0.1[Ω]、各負荷は無誘導負荷とし、その他の定数は無視するものとする。
(1) 0.72 (2) 1.44 (3) 1.80 (4) 2.16 (5) 2.88
1999年(平成11年)問12 過去問解説
Ia:Ib=1:2 なので、Ib=2Ia となります。キルヒホッフの法則を適用すると、中性線には Ia の電流が流れることになります。
一次容量[V・A]=二次容量[V・A]の関係より、
6300×3=105×Ia+105×2Ia
Ia=60[A]
線路損失 PL は
PL = Ia2×0.1+Ia2×0.1+Ib2×0.1 = 2160[W]
答え (4)
2000年(平成12年)問1
一つの送電線路において、同一負荷に対して電力を供給する場合、送電電圧を 2倍にすると、送電線路の抵抗損はもとの電圧のときに比べて何倍になるか。その倍率として、正しいものは次のうちどれか。
(1) 4倍 (2) 2倍 (3) 1倍 (4) 0.5倍 (5) 0.25倍
2000年(平成12年)問1 過去問解説
線路の抵抗を r、流れる電流を I すると、1線当たりの抵抗損 PL1 は、
$P_{L1}=I^2r$
電圧を 2倍にすると、電流は半分になります。電圧を 2倍にした後の、1線当たりの抵抗損 PL2 は、
$P_{L2}=\displaystyle \left(\frac{ I }{ 2 }\right)^2r=\displaystyle \frac{ I^2r }{ 4 }$
答え (5)
2000年(平成12年)問10
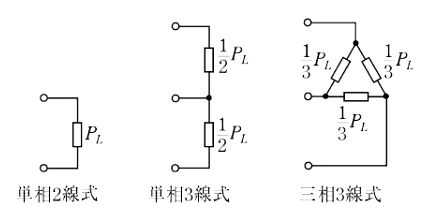
単相 100[V]の集中負荷に電力を供給するとき、100[V]単相2線式、100/200[V]単相3線式、100[V]三相3線式で供給する場合、三相3線式の線路抵抗損を1としたときの各供給方式の線路抵抗損の比として、正しいものを組み合わせたのは次のうちどれか。
ただし、3線式の場合、負荷は図のように線間に均等分割されるものとし、負荷の総容量、配電距離及び電線の材料・太さは全て同一とする。
| 単相2線式 | 単相3線式 | 三相3線式 | |
| (1) | 2 | $\displaystyle \frac{ 1 }{ 2 }$ | 1 |
| (2) | 2 | $\displaystyle \frac{ 3 }{ 4 }$ | 1 |
| (3) | 3 | $\displaystyle \frac{ 3 }{ 2 }$ | 1 |
| (4) | $\sqrt{ 3 }$ | $\displaystyle \frac{ \sqrt{ 3 } }{ 2 }$ | 1 |
| (5) | 3 | $\displaystyle \frac{ 3 }{ 4 }$ | 1 |
2000年(平成12年)問10 過去問解説
単相2線式の線電流 I1 と線路損失 PL1 は、
$I_1=\displaystyle \frac{ P }{ V }=\displaystyle \frac{ P_L }{ 100 }$
$P_{L1} = 2I_1^2r =2\displaystyle \left(\frac{ P_L }{ 100 }\right)^2r$
単相2線式の線電流 I2 と線路損失 PL2 は、
$I_2=\displaystyle \frac{ P }{ V }=\displaystyle \frac{ \frac{ P_L }{ 2 } }{ 100 }=\displaystyle \frac{ P_L }{ 200 }$
$P_{L2}= 2I^2r =2\displaystyle \left(\frac{ P_L }{ 200 }\right)^2r=\displaystyle \frac{ 1}{ 2 }\left(\frac{ P_L }{ 100 }\right)^2r$
三相3線式の線電流 I3 と線路損失 PL3 は、
$I_3=\displaystyle \frac{ P }{ \sqrt{ 3 }V }=\displaystyle \frac{ \frac{ P_L }{ 3 } ×3}{ \sqrt{ 3 }×100 }=\displaystyle \frac{ P_L }{ \sqrt{ 3 }×100 }$
$P_{L3} = 3I^2r=3\displaystyle \left(\frac{ P_L }{ \sqrt{ 3 }×100 }\right)^2r=\displaystyle \left(\frac{ P_L }{ 100 }\right)^2r$
答え (1)
2002年(平成14年)問9
負荷電力 P1[KW]、力率 cosθ1(遅れ)の負荷に電力を供給している三相3線式高圧配電線路がある。負荷電力が P1[KW]から P2[KW]に、力率 cosθ1が(遅れ)から cosθ2(遅れ)に変わったが、線路損失の変化はなかった。このときの $\displaystyle \frac{ P_1 }{ P_2}$ の値を示す式として、正しいのは次のうちどれか。
ただし、負荷の端子電圧は変わらないものとする。
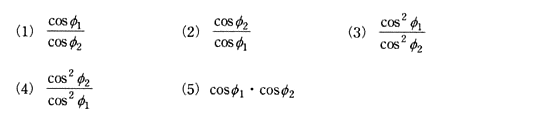
2002年(平成14年)問9 過去問解説
線路損失の変化はなかったので、線路電流は同じになります。負荷の端子電圧も変わらないので、負荷電力 P1, P2 は
$P_1=\sqrt{ 3 }VIcosθ_1×10^{-3}$
$P_2=\sqrt{ 3 }VIcosθ_2×10^{-3}$
したがって、$\displaystyle \frac{ P_1 }{ P_2}$ は
$\begin{eqnarray}\displaystyle \frac{ P_1 }{ P_2}&=&\displaystyle \frac{ \sqrt{ 3 }VIcosθ_1 ×10^{-3}}{ \sqrt{ 3 }VIcosθ_2×10^{-3}}\\\\&=&\displaystyle \frac{ cosθ_1 }{ cosθ_2}\end{eqnarray}$
答え (1)
2005年(平成17年)問9
受電端電圧が 20[kV]の三相3線式の送電線路において、受電端での電力が 2000[kW]、力率が 0.9(遅れ)である場合、この送電線路での抵抗による全電力損失[kW]の値として、最も近いのは次のうちどれか。
ただし、送電線1線当たりの抵抗値は 8[Ω]とし、線路のインダクタンスは無視するものとする。
(1) 33.3 (2) 57.8 (3) 98.8 (4) 171 (5) 333
2005年(平成17年)問9 過去問解説
三相3線式の線路損失 PL[W]は、
$\begin{eqnarray}P_{L} &=& 3I^2r = \displaystyle \frac{ P^2r }{ (Vcosθ)^2 } \\\\&=& \displaystyle \frac{ (2000×10^3)^2×8 }{ (20×10^3×0.9)^2 }\\\\&≒&98800[W]\end{eqnarray}$
答え (3)
2006年(平成18年)問16
三相3線式1回線の専用配電線がある。変電所の送り出し電圧が 6600[V]、端末にある負荷の端子電圧が 6450[V]、力率が遅れの 70[%]であるとき、次の(a)及び(b)に答えよ。
ただし、電線1線当たりの抵抗は 0.45[Ω/km]、リアクタンスは 0.35[Ω/km]、電線こう長は 5[km]とする。
(a) この負荷に供給される電力 W1[kW]の値として、最も近いのは次のうちどれか。
(1) 180 (2) 200 (3) 220 (4) 240 (5) 260
(b) 負荷が遅れ力率 80[%]、W2[kW]に変化したが線路損失は変わらなかった。W2[kW]の値として、最も近いのは次のうちどれか。
(1) 254 (2) 274 (3) 294 (4) 314 (5) 334
2006年(平成18年)問16 過去問解説
(a) 電線1線当たりの抵抗 r[Ω]、リアクタンス x[Ω]は、
r=0.45×5=2.25[Ω]
x=0.35×5=1.75[Ω]
電圧降下の近似式より
$V_L=Vs-Vr≒\sqrt{ 3 }I(rcosθ+xsinθ)$
$6600-6450≒\sqrt{ 3 }I(2.25×0.7+1.75×\sqrt{ 1-0.7^2 })$
$I≒30.7$[A]
負荷に供給される電力 W1 は、
$\begin{eqnarray}W_1&=&\sqrt{ 3 }VrIcosθ\\&=&\sqrt{ 3 }×6450×30.7×0.7\\&=&240×10^3[W]\end{eqnarray}$
答え (4)
(b) 線路損失が変わらないので、電流の大きさは同じになります。電圧降下を VL2[V]とすると、
$\begin{eqnarray}V_{L2}&=&\sqrt{ 3 }I(rcosθ+xsinθ)\\&=&\sqrt{ 3 }×30.7(2.25×0.8+1.75×\sqrt{ 1-0.8^2 })\\&≒&152[V]\end{eqnarray}$
端子電圧 Vr2 は
$V_L=Vs-Vr_2$
$152=6600-Vr_2$
$Vr_2=6448$[V]
負荷に供給される電力 W2 は、
$\begin{eqnarray}W_2&=&\sqrt{ 3 }Vr_2Icosθ\\&=&\sqrt{ 3 }×6448×30.7×0.8\\&=&274×10^3[W]\end{eqnarray}$
答え (2)
2007年(平成19年)問10
三相3線式交流送電線があり、電線1線当たりの抵抗が R[Ω]、受電端の線間電圧が Vr[V]である。いま、受電端から力率 cosθの負荷に三相電力 P[W]を供給しているものとする。
この送電線での3線の電力損失をPLとすると、PL/Pを表す式として、正しいのは次のうちどれか。
ただし、線路のインダクタンス、静電容量及びコンダクタンスは無視できるものとする。
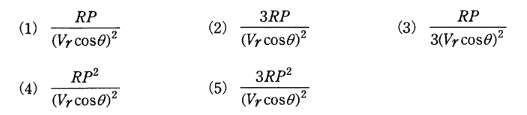
2007年(平成19年)問10 過去問解説
三相3線式の線路損失 PL は、
$P_{L} = 3I^2R = \displaystyle \frac{ P^2R }{ (Vrcosθ)^2 } $
線路損失率 $\displaystyle \frac{ P_{L} }{ P } $ は、
$\displaystyle \frac{ P_{L} }{ P }= \displaystyle \frac{ PR }{ (Vrcosθ)^2 } $
答え (1)
2008年(平成20年)問17
図のような三相高圧配電線路A-Bがある。B点の負荷に電力を供給するとき、次の(a)及び(b)に答えよ。
ただし、配電線路の使用電線は硬銅より線で、その抵抗率は 1/55[Ω・mm2/m]、線路の誘導性リアクタンスは無視するものとし、A点の電圧は三相対称であり、その線間電圧は 6600[V]で一定とする。また、B点の負荷は三相平衡負荷とし、一相当たりの負荷電流は 200[A]、力率 100[%]で一定とする。
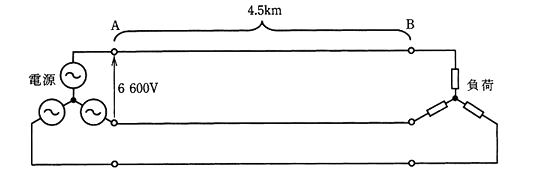
(a) 配電線路の使用電線が各相とも硬銅より線の断面積が 60[mm2]であったとき、負荷 B点における線間電圧[V]の値として、最も近いのは次のうちどれか。
(1) 6055 (2) 6128 (3) 6205 (4) 6297 (5) 6327
(b) 配電線路A-B間の線間の電圧降下を 300[V]以内にすることができる電線の断面積[mm2] を次のうちから選ぶとすれば、最小のものはどれか。
ただし、電線は各相とも同じ断面積とする。
(1) 60 (2) 80 (3) 100 (4) 120 (5) 150
2008年(平成20年)問17 過去問解説
(a) AB間の電線 1本の抵抗 R[Ω]とすると、
$R= \displaystyle \frac{ 1 }{ 55 } ×\frac{ 4500 }{ 60 }≒1.36$
負荷 B点における線間電圧 Vr[V]は、
$Vs-Vr≒\sqrt{ 3 }I(rcosθ+xsinθ)$
$6600-Vr≒\sqrt{ 3 }×200×1.36$
$Vr≒6128$[V]
答え (2)
(b) AB間の電圧降下を 300V 以内にするときの電線 1本の抵抗を R300[Ω]とすると、
$V_L≧\sqrt{ 3 }I(rcosθ+xsinθ)$
$300≧\sqrt{ 3 }×200×R_{300}$
$R_{300}≦0.866$[Ω]
求める断面積を S[mm2]とすると、
$\displaystyle \frac{ 1 }{ 55 } ×\frac{ 4500 }{ S }≦0.866$
$S≧94.47$[mm2]
答え (3)
2009年(平成21年)問10
こう長 2[km]の交流三相3線式の高圧配電線路があり、その端末に受電電圧 6500[V]、遅れ力率 80[%]で消費電力 400[kW]の三相負荷が接続されている。
いま、この三相負荷を力率 100[%]で消費電力 400[kW]のものに切り替えたうえで,受電電圧を 6500[V]に保つ。高圧配電線路での電圧降下は、三相負荷を切り替える前と比べて何倍になるか、最も近いのは次のうちどれか。
ただし、高圧配電線路の1線当たりの線路定数は、抵抗が 0.3[Ω/km]、誘導性リアクタンスが 0.4[Ω/km]とする。また,送電端電圧と受電端電圧との相差角は小さいものとする。
(1) 1.6 (2) 1.3 (3) 0.8 (4) 0.6 (5) 0.5
2009年(平成21年)問10 過去問解説
電線1線当たりの抵抗 r[Ω]、リアクタンス x[Ω]は、
$r=0.3×2=0.6$[Ω]
$x=0.4×2=0.8$[Ω]
力率 80[%]のときの電流を I1[A]、電圧降下を VL1[V]とすれば、
$P=\sqrt{ 3 }VrI_1cosθ$
$400×10^3=\sqrt{ 3 }×6500×I_1×0.8$
$I_1≒44.4$[A]
$V_{L1}≒\sqrt{ 3 }I_1(rcosθ+xsinθ)$
$V_{L1}≒\sqrt{ 3 }×44.4(0.6×0.8+0.8×\sqrt{ 1-0.8^2 })$
$V_{L1}≒73.8$[V]
力率 100[%]のときの電流を I2[A]、電圧降下を VL2[V]とすれば、
$P=\sqrt{ 3 }VrI_2cosθ$
$400×10^3=\sqrt{ 3 }×6500×I_2×1.0$
$I_2≒35.5$[A]
$V_{L2}≒\sqrt{ 3 }I_2(rcosθ+xsinθ)$
$V_{L2}≒\sqrt{ 3 }×35.5(0.6×1.0+0.8×0)$
$V_{L2}≒36.9$[V]
三相負荷を切り替える前と比べた電圧降下の倍率は
$\displaystyle \frac{ V_{L2} }{ V_{L1} }=\displaystyle \frac{ 36.9 }{ 73.8 }=0.5$
答え (5)
2011年(平成23年)問17
単相2 線式配電線があり、この末端に 300[kW]の需要家がある。
この配電線の途中、図に示す位置に 6300[V]/6900[V]の昇圧器を設置して受電端電圧を 6600[V]に保つとき、次の(a)及び(b)の問に答えよ。
ただし、配電線の1線当たりの抵抗は 1[Ω/km]、リアクタンスは 1.5[Ω/km]とし、昇圧器のインピーダンスは無視するものとする。
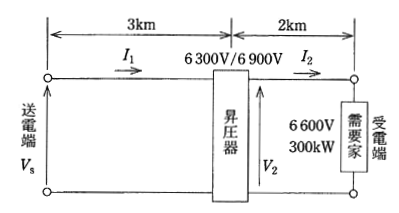
(a) 末端の需要家が力率1の場合、受電端電圧を 6600[V]に保つとき、昇圧器の二次側の電圧 V2[V]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 6691 (2) 6757 (3) 6784 (4) 6873 (5) 7055
(b) 末端の需要家が遅れ力率 0.8の場合、受電端電圧を 6600[V]に保つとき、送電端の電圧 VS[V]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 6491 (2) 6519 (3) 6880 (4) 7016 (5) 7189
2011年(平成23年)問17 過去問解説
(a) 受電端電圧を 6600[V]に保つときの昇圧器2次側の電流 I2[A]は、
$P=I_2V$
$300×10^3=I_2×6600$
$I_2=45.45$ [A]
電圧降下を $V_L$ とすると、
$\begin{eqnarray}V_L&=&2I(rcosθ+xsinθ)\\&=&2×45.45(2×1+3.0×0)=181.8[V]\end{eqnarray}$
$V_L=V_2-Vr$ より
$V_2=6600+182=6782$[V]
答え (3)
(b) 力率 0.8で受電端電圧を 6600[V]に保つときの昇圧器2次側の電流 I2[A]は、
$I_2=\displaystyle \frac{ 300×10^3 }{ 6600×0.8 }=56.81$[A]
電圧降下を VL2$ とすると、
$\begin{eqnarray}V_{L2}&=&2I(rcosθ+xsinθ)\\&=&2×56.81(2×0.8+3.0×\sqrt{ 1-0.8^2 })=386.3[V]\end{eqnarray}$
$V_2=6600+386.3=6986.3$[V]
昇圧器1次側の電圧 V1[V]と電流 I1[A]は
$V_1=\displaystyle \frac{ 6986.3×6300 }{ 6900 }=6378.8$[V]
$I_1=\displaystyle \frac{ 56.81×6300 }{ 6900 }=62.22$[A]
電圧降下を VL1 とすると、
$V_{L1}≒2×62.22(3×0.8+4.5×\sqrt{ 1-0.8^2 })=634.6$[V]
$V_L=V_S-V1$ より
$V_S=6378.8+634.6=7013.4$ [V]
答え (4)
2012年(平成24年)問10
こう長 20[km]の三相3線式2回線の送電線路がある。受電端で 33[kV]、6600[kW]、力率 0.9 の三相負荷に供給する場合、受電端電力に対する送電損失を 5[%]以下にするための電線の最小断面積[mm2]の値として、計算値が最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、使用電線は、断面積 1[mm2]、長さ 1[m]当たりの抵抗を 1/35[Ω]とし、その他の条件は無視する。
(1) 14.3 (2) 23.4 (3) 24.7 (4) 42.8 (5) 171
2012年(平成24年)問10 過去問解説
三相3線式1回線分に流れる電流 I[A]は、
$P=\sqrt{ 3 }VrIcosθ$
$6600×10^3=\sqrt{ 3 }×33×10^3×2I×0.9$
$I≒64.15$[A]
6線分の線路損失 PL = 6I2r [W]で、抵抗を r とすると、題意より
$0.05P ≧ 6I^2r $
$0.05×6600×10^3 ≧ 6×64.15^2r $
$r≦13.37$[Ω]
求める断面積を S[mm2]とすると、
$\displaystyle \frac{ 1 }{ 35 } ×\frac{ 20×10^3 }{ S }≦13.37$
$S≧42.74$[mm2]
答え (4)
2012年(平成24年)問16
三相3線式1回線無負荷送電線の送電端に線間電圧 66.0[kV]を加えると、受電端の線間電圧は 72.0[kV]、1線当たりの送電端電流は 30.0[A]であった。この送電線が、線路アドミタンス B[mS]と線路リアクタンス X[Ω]を用いて、図に示す等価回路で表現できるとき、次の(a)及び(b)の問に答えよ。
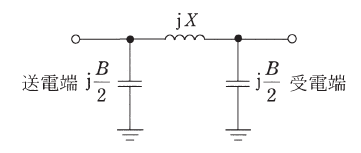
(a) 線路アドミタンス B[mS]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.217 (2) 0.377 (3) 0.435 (4) 0.545 (5) 0.753
(b) 線路リアクタンス X[Ω]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 222 (2) 306 (3) 384 (4) 443 (5) 770
2012年(平成24年)問16 過去問解説
(a) 図のように電流を $\dot{I}$,$\dot{I_1}$,$\dot{I_2}$ とすると、無負荷ですので、
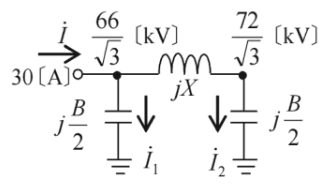
$\dot{I}=\dot{I_1}+\dot{I_2}$
$=\displaystyle\frac{66×10^3}{\sqrt{3}}・\displaystyle\frac{B}{2}+\displaystyle\frac{72×10^3}{\sqrt{3}}・\displaystyle\frac{B}{2}$
$30=\displaystyle\frac{B}{2}\left(\displaystyle\frac{66×10^3}{\sqrt{3}}+\displaystyle\frac{72×10^3}{\sqrt{3}}\right)$
$B≒0.753$[mS]
答え (5)
(b) $\dot{I_2}$ を求めます。
$\dot{I_2}=\displaystyle\frac{72×10^3}{\sqrt{3}}・\displaystyle\frac{B}{2}$
$=\displaystyle\frac{72×10^3}{\sqrt{3}}・\displaystyle\frac{0.753×10^{-3}}{2}≒15.65$[A]
電圧降下 $V_L$ は、
$V_L=\sqrt{3}\dot{I_2}X$
$(72-66)×10^3=\sqrt{3}×15.65X$
$X≒222$[Ω]
答え (1)
2014年(平成26年)問7
こう長 2kmの三相3線式配電線路が、遅れ力率 85%の平衡三相負荷に電力を供給している。負荷の端子電圧を 6.6kVに保ったまま、線路の電圧降下率が 5.0%を超えないようにするための負荷電力の最大値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、1km1線当たりの抵抗は 0.45Ω、リアクタンスは 0.25Ωとし、その他の条件は無いものとする。なお、本問では送電端電圧と受電端電圧との相差角が小さいとして得られる近似式を用いて解答すること。
(1) 1023 (2) 1799 (3) 2117 (4) 3117 (5) 3600
2014年(平成26年)問7 過去問解説
電圧降下を VL=Vs-Vr[V]とすると、電圧降下率 ε[%]は
$ε=\displaystyle \frac{ V_L }{ Vr }$
$V_L≒\sqrt{ 3 }I(rcosθ+xsinθ)$ より
$0.05≧\displaystyle \frac{ \sqrt{ 3 }I(0.45×2×0.85+0.25×2×\sqrt{ 1-0.85^2 }) }{ 6600 }$
$I≦185$[A]
負荷電力の最大値は
$P_{max}=\sqrt{ 3 }×6600×185×0.85≒180×10^4$[W]
答え (2)
2016年(平成28年)問9
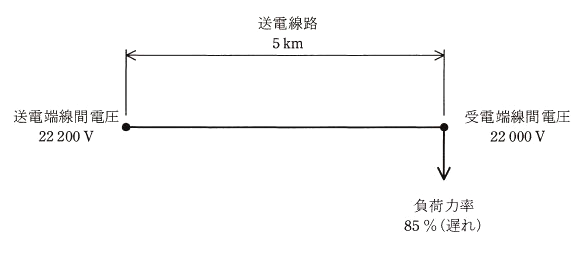
図のように、こう長 5kmの三相3線式1回線の送電線路がある。この送電線路における送電端線間電圧が 22200V、受電端線間電圧が 22000V、負荷力率が 85%(遅れ)であるとき、負荷の有効電力 [kW] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、1km当たりの電線1線の抵抗は 0.182Ω、リアクタンスは 0.355Ωとし、その他の条件はないものとする。なお、本問では、送電端線間電圧と受電端線間電圧との位相角は小さいとして得られる近似式を用いて解答すること。
(1) 568 (2) 937 (3) 2189 (4) 3277 (5) 5675
2016年(平成28年)問9 過去問解説
電線1線当たりの抵抗 r[Ω]、リアクタンス x[Ω]は、
$r=0.182×5=0.91$[Ω]
$x=0.355×5=1.775$[Ω]
電圧降下の近似式より
$V_L=Vs-Vr≒\sqrt{ 3 }I(rcosθ+xsinθ)$
$22200-22000≒\sqrt{ 3 }I(0.91×0.85+1.775×\sqrt{ 1-0.85^2 })$
$I=67.58$[A]
負荷の有効電力P[kW]は、
$P=\sqrt{ 3 }VrIcosθ$
$=\sqrt{ 3 }×22000×67.58×0.85$
$=2189×10^3$
答え (3)
2017年(平成29年)問11
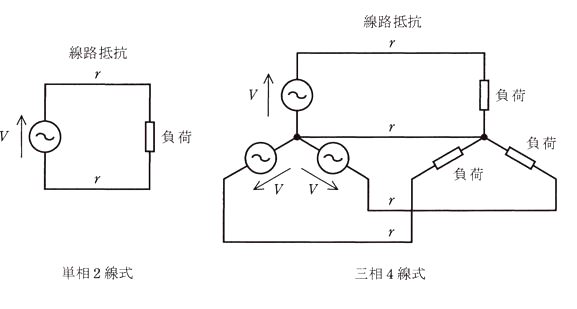
回路図のような単相2線式及び三相4線式のそれぞれの低圧配電方式で、抵抗負荷に送電したところ送電電力が等しかった。
このときの三相4線式の線路損失は単相2線式の何 [%] となるか。最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、三相4線式の結線はY結線で、電源は三相対称、負荷は三相平衡であり、それぞれの低圧配電方式の1線当たりの線路抵抗r、回路図に示す電圧Vは等しいものとする。また、線路インダクタンスは無視できるものとする。
(1) 16.7 (2) 33.3 (3) 50.0 (4) 57.8 (5) 66.7
2017年(平成29年)問11 過去問解説
単相2線式及び三相4線式の、どちらの送電電力も等しかったので、この電力を P[W]とすると、
単相2線式
$P=VI_1cosθ$
三相 4 線式の場合
$P=3VI_4cosθ$
P=VI1cosθ=3VI4cosθ なので、
$I_1=3I_4$
単相2線式の線路損失と三相4線式の線路損失を、それぞれ PL1、PL4 とすると、
$P_{L1}=2I_1r^2$
$P_{L4}=3I_4r^2$
よって、$\displaystyle \frac{ P_{L4} }{ P_{L1} }$ は、
$\displaystyle \frac{ P_{L4} }{ P_{L1} }=\displaystyle \frac{ 3I_4r^2 }{ 3I_4r^2 }≒0.167$
答え (1)





