このページでは、キルヒホッフの法則とブリッジ回路の合成抵抗について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題されたキルヒホッフの法則とブリッジ回路の合成抵抗の過去問題の求め方も解説しています。
キルヒホッフの法則
第1法則
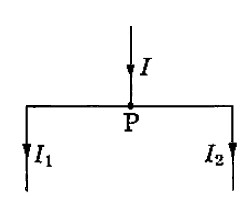
回路の接続点における流入する電流の総和は、流出する電流の総和に等しい。
$I=I_1+I_2$
第2法則
キルヒホッフの法則 例題
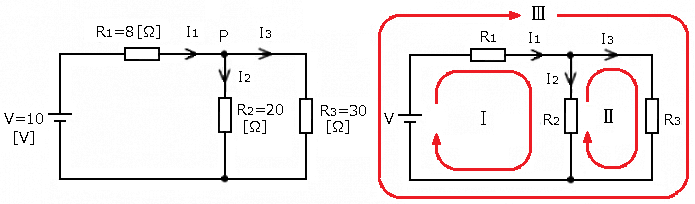
キルヒホッフの法則を使って回路に流れる電流 $I_1$,$I_2$,$I_3$ を求めます。キルヒホッフの第1法則は、「回路の接続点における流入する電流の総和は、流出する電流の総和に等しい」ですので、
$I_1=I_2+I_3$ … (1)
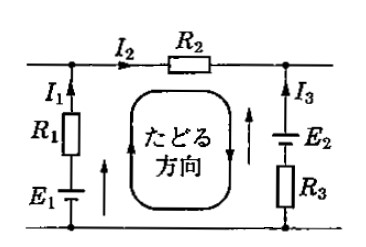
キルヒホッフの第2法則は、「任意の閉回路において、たどる方向を定めると電圧降下の総和は、起電力の総和に等しい」です。図右側のように、Ⅰ,Ⅱ,Ⅲのような閉ループを作ります。ループの向きは自由に決めてください。閉ループの向きと電流の向きが逆向きの場合は電圧降下にマイナスをつけます。
閉ループⅠの式:$R_1I_1+R_2I_2=V$ … (2)
閉ループⅡの式:$R_3I_3-R_2I_2=0$ … (3)
閉ループⅢの式:$R_1I_1+R_3I_3=V$ … (4)
(1)~(4)の4式ができましたが、未知数が3つなので、この中から3式を選んで連立方程式を解くと $I_1$,$I_2$,$I_3$ を求めることができます。
(2)と(3)式に $R_1$,$R_2$,$R_3$,$V$ の数値を代入すると、
$8I_1+20I_2=10$ … (2)’
$30I_3-20I_2=0$ … (3)’
(1)式を(2)’に代入すると
$8(I_2+I_3)+20I_2=10$
$28I_2+8I_3=10$… (5)
(3)’と(5)式を解くと、$I_1=0.5$ ,$I_2=0.3$ ,$I_3=0.2$ となります。
キルヒホッフの法則 ループ電流法
キルヒホッフの法則を利用した解き方で、ループ電流法というものがあります。キルヒホッフの法則の例題と同じ回路をループ電流法で解いてみます。
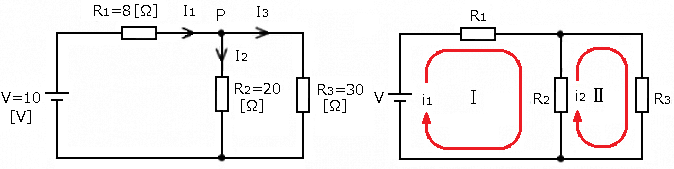
右側の図のように、閉ループに電流 $i_1$,$i_2$ が流れていると仮定します。キルヒホッフの第2法則から、次の式が成り立ちます。
閉ループⅠの式:$R_1i_1+R_2(i_1-i_2)=V$ … (1)
閉ループⅡの式:$R_3i_2+R_2(i_2-i_1)=0$ … (2)
(1)と(2)式に $R_1$ ,$R_2$,$R_3$,$V$ の数値を代入すると、
$8i_1+20(i_1-I_2)=10$
$28i_1-20I_2=10$
$14i_1-10I_2=5$ … (1)’
$30i_2+20(i_2-i_1)=0$
$50i_2-20i_1=0$
$2i_1=5i_2$ … (2)’
(1)’と(2)’式を解くと、$i_1=0.5$,$i_2=0.2$ と求まります。$i_1$,$i_2$ と $I_1$,$I_2$,$I_3$ の関係は
$I_1=i_1$
$I_2=i_1-i_2$
$I_3=i_3$
となりますので、$I_1=0.5$ ,$I_2=0.3$ ,$I_3=0.2$ と求めることができます。
対称回路を応用したテクニック
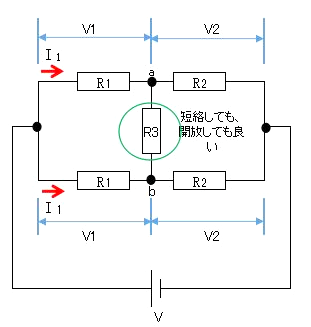
対称回路とは、上下とも同じ抵抗値の回路です。このような回路では上側に流れる電流と下側に流れる電流は、同じ値になります。電流が同じ値ということは、上下の $R_1$ で電圧降下も同じです。
a 端子と b 端子に電位差がないということで、ab 間には電流が流れません。つまり、「短絡しても開放しても流れる電流は変化しません。」
この電圧降下の考え方を応用して、下図のような回路で $R_3$ に流れる電流を考えてみます。尚、このような回路を不平衡ブリッジ回路といいます。
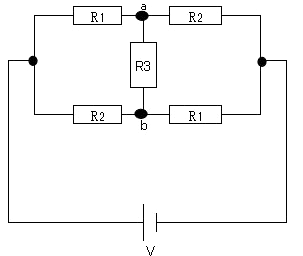
ブリッジ回路の場合は、まずは「平衡条件を満たしているかどうか」を見ることが先決です。満たされていない場合、どのように解いていくのかを説明します。
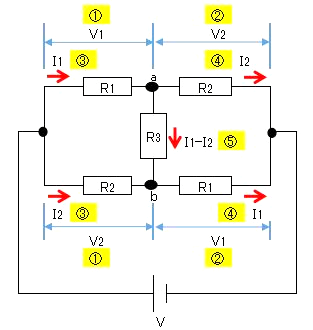
- 上側の回路の $R_1$ の電圧を $V_1$、下側の回路の $R_2$ の電圧を $V_2$とします。
- 上側の回路の合計電圧と下側の回路の合計電圧は $V$ で等しくならなければなりません。つまり、上側の回路の $R_2$ の電圧は $V_2$、下側の回路の $R_1$ の電圧は $V_1$になります。
- 上側の回路に流れる電流を $I_1$、下側の回路に流れる電流を $I_2$ とします。上側の回路の $R_1$ の電圧降下は $V_1$ です。下側の回路の $R_2$ の電圧降下は $V_2$ です。
- 下側の回路の $R_1$ の電圧降下は $V_1$ です。上側の回路の $R_2$ の電圧降下は $V_2$ です。
つまり、上側の回路と下側の回路の $R_1$ に流れる電流は等しくなければなりません。
同様に、下側の回路と上側の回路の $R_2$ に流れる電流は等しくなければなりません。 - キルヒホッフの第1法則より $R_3$ に流れる電流は $I_1-I_2$ になります。
(注意)回路は直列と並列が入り混じっていますので、分流の法則や分圧の法則は単純には使えません。この手の問題は非常に計算が複雑になりますので、注意してください。
この考え方を使えば電流比の計算が楽になります。非常に便利ですので、テクニックとして覚えておきましょう。
不平衡ブリッジ回路の電流値や抵抗値を求める
- キルヒホッフの法則で解く
計算が非常にややこしくなり、間違いやすいです。 - スターデルタ変換で解く
変換の公式を覚えていれば、わりと楽に解答できます。 - 鳳テブナンの定理で解く
電圧降下の考え方を理解していれば簡単に解けます。
この3つが主な解き方となります。3の鳳テブナンの定理については、別のページで解説します。
キルヒホッフの法則で解く
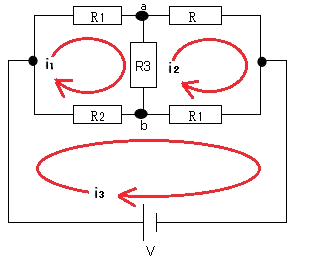
キルヒホッフのループ電流法を使って、未知数分の式をたて、方程式を計算していきます。計算が複雑になり、時間がかかることと、間違いやすいのが欠点です。
簡単に解く方法を思い浮かばないときに、使いましょう。尚、どのような回路でも、ほぼ解くことができます。
スターデルタ変換で解く
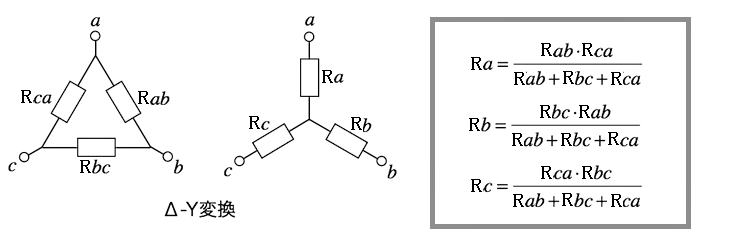
図はΔ-Y変換公式です。複雑な電気回路の合成抵抗等を求める場合によく使われます。一見すると複雑な公式で覚えるのに苦労しそうですが、次の図をイメージすると、とても単純に覚えられます。

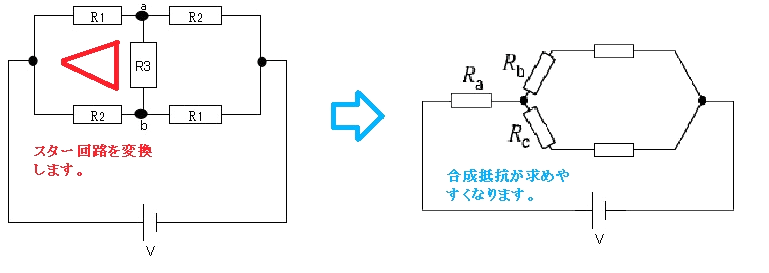
スターデルタ変換を不平衡ブリッジ回路に当てはめてみます。
$Ra=\displaystyle \frac{R_1R_2 }{ R1+R2+R3}$
$Rb=\displaystyle \frac{R_1R_3 }{ R1+R2+R3}$
$Rc=\displaystyle \frac{R_2R_3 }{ R1+R2+R3}$
右図のように、直並列の回路に変換できますので、不平衡ブリッジ回路の電流値や抵抗値を求めることができます。
電験三種-理論(直流回路)過去問題
1997年(平成9年)問12
図のような直流回路において、電流の比 $\displaystyle \frac{I_1}{ I_2}$ はいくらか。正しい値を次のうちから選べ。
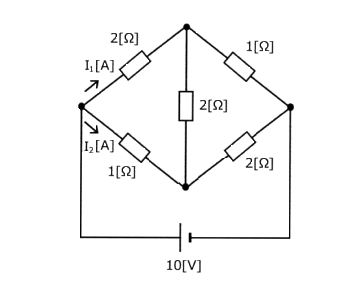
(1) 0.43 (2) 0.57 (3) 0.75 (4) 1.33 (5) 1.75
1997年(平成9年)問12 過去問解説
回路は対称になっているので、図のように電流が流れます。
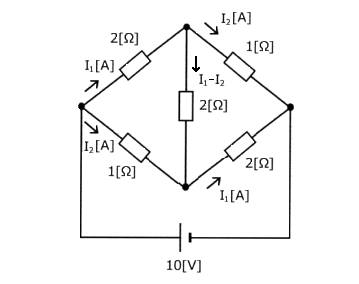
回路の左部分のΔ閉ループを、キルヒホッフの第二法則を適用すると、
$2I_1+2(I_1-I_2)-I_2=0$
$4I_1=3I_2$
$\displaystyle \frac{I_1}{ I_2}=0.75$
答え (3)
2001年(平成13年)問10
図のような直流回路において、$2R$[Ω]の抵抗に流れる電流 $I$[A]の値として、正しいものは次のうちどれか。
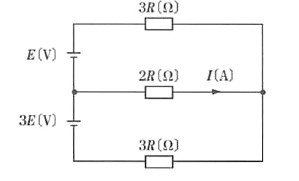
(1) $\displaystyle \frac{2E}{ 7R}$ (2) $\displaystyle \frac{5E}{ 6R}$ (3) $\displaystyle \frac{E}{ 6R}$ (4) $\displaystyle \frac{3E}{ 4R}$ (5) $\displaystyle \frac{E}{ 2R}$
2001年(平成13年)問10 過去問解説
図のように電流の方向を仮定して、キルヒホッフの法則を使います。
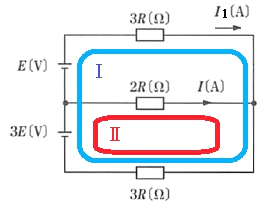
Ⅰの閉回路
$3E+E=3RI_1+3R(I+I_1)$
$4E=6RI_1+3RI$ … (1)
Ⅱの閉回路
$3E=2RI+3R(I+I_1)$
$3E=3RI_1+5RI$ … (2)
(1),(2)式より $I_1$ を消去すると、
$2E=7RI$
$I=\displaystyle \frac{2E}{ 7R}$
答え (1)
2003年(平成15年)問5
図のような直流回路において、抵抗 6[Ω]の端子間電圧の大きさ $V$[V]の値として、正しいものは次のうちどれか。
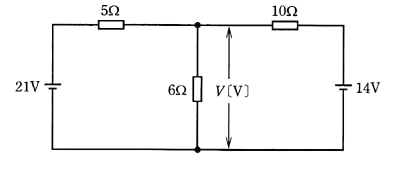
(1) 2 (2) 5 (3) 7 (4) 12 (5) 15
2003年(平成15年)問5 過去問解説
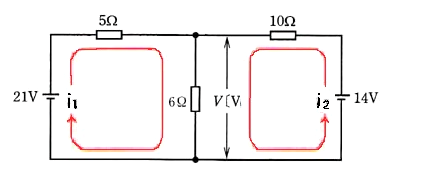
閉ループに電流 $i_1$、$i_2$ が流れていると仮定します。
左側のループ
$5i_1+6(i_1+i_2)=21$
$11i_1+6i_2=21$ …(1)
右側のループ
$10i_2+6(i_1+i_2)=14$
$3i_1+8i_2=7$ …(2)
(2)式×11
$33i_1+88i_2=77$ …(2)’
(1)式×3
$33i_1+18i_2=63$ …(1)’
(2)’式-(1)’式
$70i_2=14$
$i_2=0.2$[A]
$i_2=0.2$を(2)式に代入
$3I_1+8×0.2=7$
$i_1=1.8$[A]
6[Ω]の抵抗に流れる電流は、$i_1+i_2=2$[A]なので
$V=2×6=12$[Ω]
答え (4)
2005年(平成17年)問15
図の直流回路において、次の(a)及び(b)に答えよ。ただし、電源電圧 $E$[V]の値は一定で変化しないものとする。
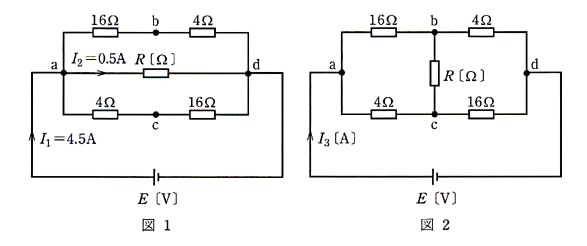
(a) 図1のように抵抗 $R$[Ω]を端子a,b間に接続したとき、$I_1=4.5$[A],$I_2=0.5$[A]の電流が流れた。抵抗 $R$[Ω]の値として、正のは次のうちどれか。
(1) 20 (2) 40 (3) 80 (4) 160 (5) 180
(b) 図1の抵抗 $R$[Ω]を図2のように端子 b,c 間に接続し直したとき、回路に流れる電流 $I_3$[A]の値として、最も近いのは次のうちどれか。
(1) 4.0 (2) 4.2 (3) 4.5 (4) 4.8 (5) 5.5
2005年(平成17年)問15 過去問解説
(a) 図1の回路の抵抗を合成した等価回路は下図のようになります。
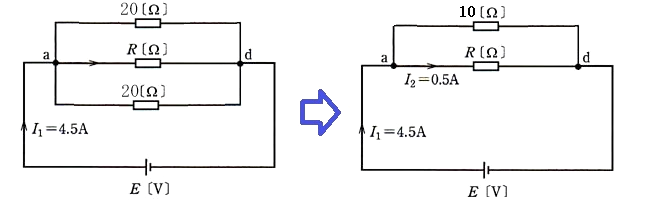
分流の法則より
$0.5=\displaystyle \frac{10 }{ R+10 }×4.5$
$R+10=10×9$
$R=80$[Ω]
答え (3)
(b) 図2をΔ-Y変換で考えます。
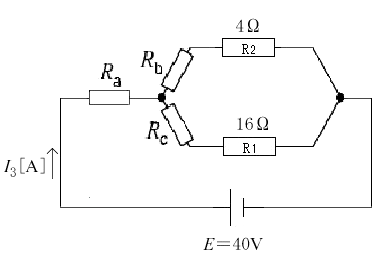
$Ra=\displaystyle \frac{16×4 }{ 16+4+80}=0.64$[Ω]
$Rb=\displaystyle \frac{16×80}{ 16+4+80}=12.8$[Ω]
$Rc=\displaystyle \frac{4×80}{ 16+4+80}=3.2$[Ω]
回路の合成抵抗$R$は
$R=0.64+\displaystyle \frac{(12.8+4)(3.2+16)}{ (12.8+4)+(3.2+16)}=9.6$[Ω]
よって
$9.6I_3=40$
$I_3=4.17$
答え (2)
2008年(平成20年)問7
図のように、2種類の直流電源と3種類の抵抗からなる回路がある。各抵抗に流れる電流を図に示す向きに定義するとき、電流 $I_1$[A],$I_2$[A],$I_3$[A]の値として、正しいものを組み合わせたものは次のうちどれか。
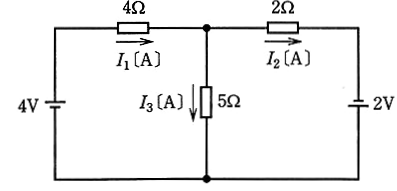
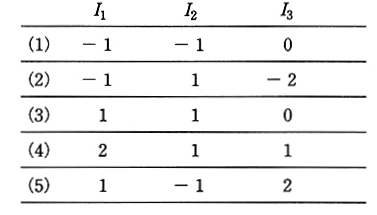
2008年(平成20年)問7 過去問解説
図のように電流の方向を仮定して、キルヒホッフの法則を使います。
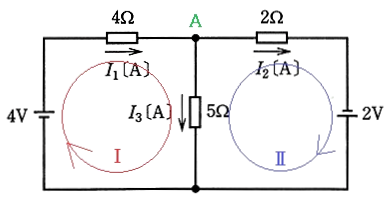
A点での電流の総和は、
$I_1=I_2+I_3$ … (1)
Ⅰの閉回路
$4=4I_1+5I_3$ … (2)
Ⅱの閉回路
$2=2I_2-5I_3$ … (3)
(1),(2),(3)を解くと、
$I_1=1$ , $I_2=1$ , $I_3=0$
答え (3)