第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の電力科目に出題される「汽力発電所の熱効率」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の電力科目の試験で、実際に出題された「汽力発電所の熱効率」の過去問題も解説しています。
- 汽力発電所の熱効率
- 各種公式
- 公式集
- 電験三種-電力(火力発電)過去問題
- 1999年(平成11年)問3
- 1999年(平成11年)問3 過去問解説
- 2000年(平成12年)問11
- 2000年(平成12年)問11 過去問解説
- 2001年(平成13年)問11
- 2001年(平成13年)問11 過去問解説
- 2003年(平成15年)問15
- 2003年(平成15年)問15 過去問解説
- 2004年(平成16年)問3
- 2004年(平成16年)問3 過去問解説
- 2004年(平成16年)問15
- 2004年(平成16年)問15 過去問解説
- 2007年(平成19年)問2
- 2007年(平成19年)問2 過去問解説
- 2008年(平成20年)問15
- 2008年(平成20年)問15 過去問解説
- 2010年(平成22年)問15
- 2010年(平成22年)問15 過去問解説
- 2012年(平成24年)問15
- 2012年(平成24年)問15 過去問解説
- 2013年(平成25年)問2
- 2013年(平成25年)問2 過去問解説
- 2015年(平成27年)問3
- 2015年(平成27年)問3 過去問解説
- 2016年(平成28年)問15
- 2016年(平成28年)問15 過去問解説
汽力発電所の熱効率
効率の考え方
効率とは、使った労力に対する、得られた成果の割合です。機械設備では、「仕事の量とそれに供給した総エネルギーとの比率」のことです。
効率の基本式
$効率=\displaystyle \frac{ 出力 }{ 入力 }=\displaystyle \frac{ 出力 }{ 出力+損失 }$
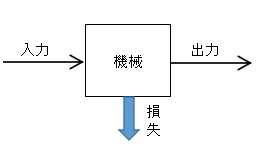
発熱量と総発熱量
固体や液体の燃料 1kg を完全燃焼させたときに発する熱量のことを「発熱量」といいます。気体燃料の場合は、体積1m3 を完全燃焼させたときに発する熱量のことを発熱量といいます。「燃焼させた燃料の重さ」と「燃料の発熱量」の積を「総発熱量」といい、次の式で求めることができます。
発熱量 H[kJ/kg]の燃料を、B[kg]燃焼させたときの総発熱量 Q[kJ]を求める式
$Q=B・H$
$Q$[kJ]:総発熱量
$B$[kg]:燃料の使用量
$H$[kJ/kg]:燃料の発熱量
尚、「燃焼により発生する総発熱量」は「燃料の保有熱量」と同じ意味になります。
汽力発電所の熱効率
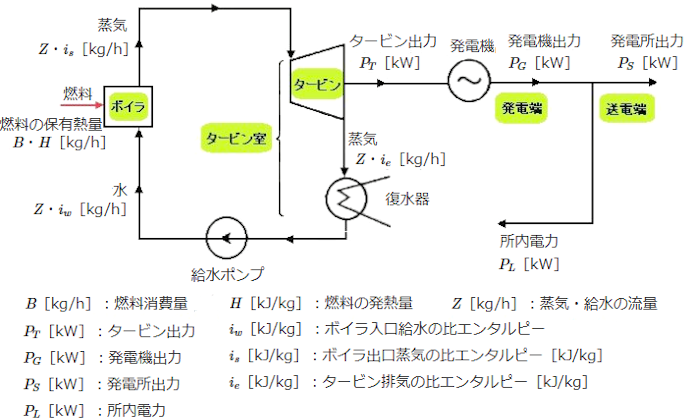
汽力発電機の熱効率 η(読み:イータ)は、「ボイラで使用した燃料の保有熱量」と「タービンの機械出力(熱量換算値)」の比をパーセントで表したものです。
汽力発電機の熱効率 η を求める式
$η=\displaystyle \frac{ 3600P_T}{ BH}×100$[%]
$B$[kg/h]:燃料消費量
$H$[kJ/kg]:燃料の発熱量
$P_T$[kW]:タービン出力
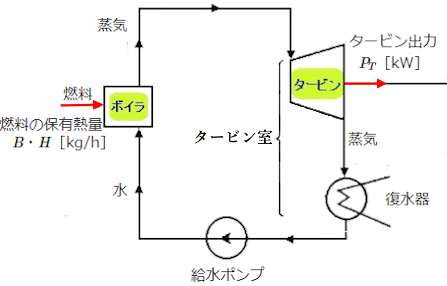
ランキンサイクルの熱効率
ランキンサイクルの熱効率には、「ボイラ効率」「ランキンサイクルの効率」「タービン効率」「タービン室効率」「発電端熱効率」「送電端熱効率」があります。ランキンサイクルの効率は、「熱サイクルの効率」とも呼ばれています。
ボイラ効率
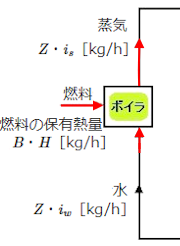
ボイラ効率 ηB は、「ボイラで使用した燃料の保有熱量」と「ボイラで発生した蒸気の熱量」の比をパーセントで表したものです。
ボイラ効率 ηB を求める式
$η_B=\displaystyle \frac{ Z(i_s-i_w) }{ BH}×100$[%]
$B$[kg/h]:燃料消費量
$H$[kJ/kg]:燃料の発熱量
$Z$[kg/h]:蒸気・給水の流量
$i_w$[kJ/kg]:ボイラ入口給水の比エンタルピー
$i_s$[kJ/kg]:ボイラ出口蒸気の比エンタルピー
エンタルピー(単位:[KJ])とは、熱エネルギーと仕事のエネルギーを持った物体のエネルギーを表す指標で、比エンタルピー(単位:[KJ/Kg])とは、単位重量当たりのエンタルピーです。
ランキンサイクル(熱サイクル)の効率
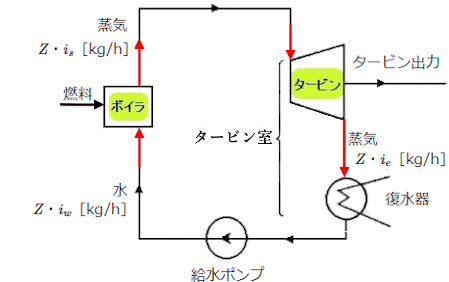
熱サイクルの効率 ηC は、「ボイラで発生した蒸気の熱量」と「タービンで消費した熱量」の比をパーセントで表したものです。
熱サイクルの効率 ηC を求める式
$\begin{eqnarray}η_C&=&\displaystyle \frac{ Z(i_s-i_e) }{ Z(i_s-i_w) }×100\\&=&\displaystyle \frac{ (i_s-i_e) }{ (i_s-i_w) }×100[\%]\end{eqnarray}$
$Z$[kg/h]:蒸気・給水の流量
$i_w$[kJ/kg]:ボイラ入口給水の比エンタルピー
$i_s$[kJ/kg]:ボイラ出口蒸気の比エンタルピー
$i_e$[kJ/kg]:タービン排気の比エンタルピー
タービン効率
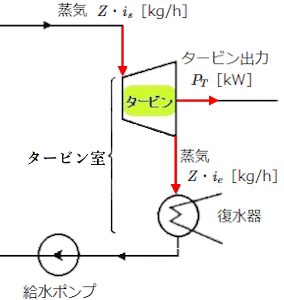
タービン効率 ηT は、「タービンで消費した熱量」と「タービン出力」の比をパーセントで表したものです。
タービン効率 ηT を求める式
$η_T=\displaystyle \frac{ 3600P_T}{ Z(i_s-i_e)}×100$[%]
$Z$[kg/h]:蒸気・給水の流量
$i_s$[kJ/kg]:ボイラ出口蒸気の比エンタルピー
$i_e$[kJ/kg]:タービン排気の比エンタルピー
$P_T$[kW]:タービン出力
タービン出力の「3600」は[kw]を[kJ]単位に換算しています。
1 W = 1 J/s ⇒ 1 W・s = 1J なので、
1kwh = 1kW × 1h(時間)
= 1kW × 3600s(秒)
= 3600kWs = 3600kJ
電力量 : 1kWh = 3600kJ
電 力 : 1kW = 3600kJ/h
タービン室効率
タービン室効率 ηTR は、「ボイラで発生した蒸気の熱量」と「タービン出力」の比をパーセントで表したものです。
タービン室効率 ηTR を求める式
$η_{TR}=\displaystyle \frac{ 3600P_T}{ Z(i_s-i_w)}×100$[%]
$Z$[kg/h]:蒸気・給水の流量
$i_w$[kJ/kg]:ボイラ入口給水の比エンタルピー
$i_s$[kJ/kg]:ボイラ出口蒸気の比エンタルピー
$P_T$[kW]:タービン出力
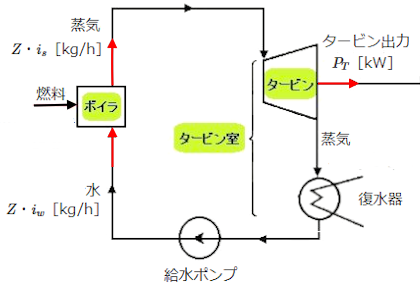
タービン室効率はタービンと復水器が一つのユニットとして考えています。タービンの機械的な出力に対する、このユニットを通る過程で蒸気が失ったエネルギーの割合を示しています。
発電端熱効率
発電端熱効率 ηP は、「ボイラで使用した燃料の保有熱量」と「発電機出力」の比をパーセントで表したものです。
発電端熱効率 ηP を求める式
$η_P=\displaystyle \frac{ 3600P_G}{ BH}×100$[%]
$B$[kg/h]:燃料消費量
$H$[kJ/kg]:燃料の発熱量
$P_G$[kW]:発電機出力
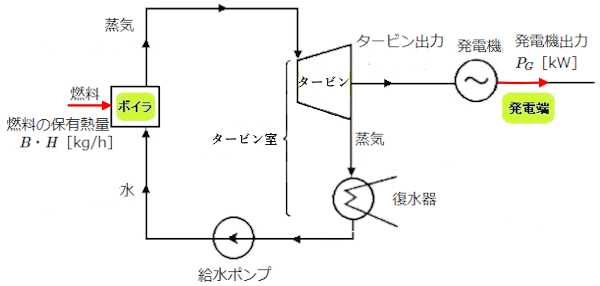
発電端熱効率 ηP は 「ボイラ効率 × タービン室効率 × 発電機効率 」で表すこともできます。
$η_P=η_Bη_{TR}η_G$[%]
$η_B$:ボイラ効率
$η_{TR}$:タービン室効率
$η_G$:発電機効率
ηG は、発電機効率を表します。
発電機効率 ηG を求める式
$\begin{eqnarray}η_G&=&\displaystyle \frac{ 発電機出力}{タービン出力 }\\\\&=&\displaystyle \frac{ P_G}{ P_T}×100[\%]\end{eqnarray}$
この公式を覚えておくと便利です
送電端熱効率
送電端熱効率 ηS は、「ボイラで使用した燃料の保有熱量」と「発電所出力」の比をパーセントで表したものです。
送電端熱効率 ηS を求める式
$η_S=\displaystyle \frac{ 3600P_S}{ BH}×100$[%]
$B$[kg/h]:燃料消費量
$H$[kJ/kg]:燃料の発熱量
$P_S$[kW]:発電所出力
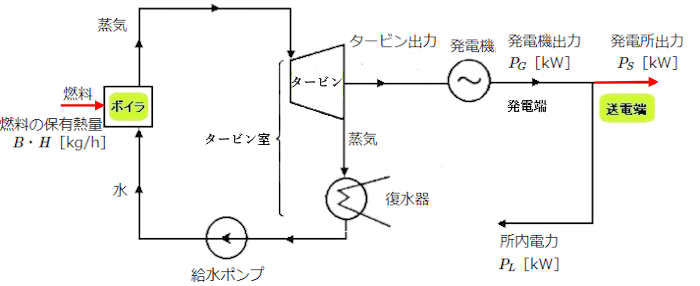
発電所で使用する電力を所内電力 PL といい、発電機出力 PG から供給されます。発電所出力 PS との関係は、
$P_S=P_G-P_L$
所内電力 PL と発電機出力 PG の比率を所内率 L といいます。
$L=\displaystyle \frac{ P_L}{ P_G}=\displaystyle \frac{ P_G-P_S}{ P_G}=1-\displaystyle \frac{ P_S}{ P_G}$
所内率 L と 発電機出力 PG がわかっている場合、発電所出力 PS を求めることができます。
$P_S = P_G (1-L)$
送電端熱効率 ηS を変形します。
$\begin{eqnarray}η_S&=&\displaystyle \frac{ 3600P_S}{ BH}×100\\\\&=&\displaystyle \frac{ 3600(P_G-P_L)}{ BH}×100\\\\&=&\displaystyle \frac{ 3600}{ BH}P_G\left(1-\displaystyle \frac{P_L}{P_G}\right)×100\\\\&=&\displaystyle \frac{ 3600P_G}{ BH}×100\left(1-\displaystyle \frac{P_L}{P_G}\right)\\\\&=&η_P\left(1-\displaystyle \frac{P_L}{P_G}\right)\\\\&=&η_P(1-L)\end{eqnarray}$
発電所出力 PS と所内率 L、送電端熱効率 ηS を求める式
発電所出力 $P_S=P_G-P_L= P_G (1-L)$
所内率 $L=\displaystyle \frac{ P_L}{ P_G}=\displaystyle \frac{ P_G-P_S}{ P_G}=1-\displaystyle \frac{ P_S}{ P_G}$
送電端熱効率 $η_S=η_P(1-L)$
$P_S$[kW]:発電所出力
$P_G$[kW]:発電機出力
$P_L$[kW]:所内電力
$L$:所内率
各種公式
熱消費率と燃料消費率
熱消費率 J とは、1[kW⋅h]の電力量を発電するのに必要な熱消費量をいいます。
$J =\displaystyle \frac{ BH}{ P_G}=\displaystyle \frac{ 3600}{ η_P}$[kJ/kW・h]
燃料消費率 F とは、1[kW⋅h]の電力量を発電するのに必要な燃料の量をいいます。
$F =\displaystyle \frac{ B}{ P_G}=\displaystyle \frac{ 3600}{ H・η_P}$[kg/kW・h]
熱消費率 J と燃料消費率 F を求める式
$J =\displaystyle \frac{ BH}{ P_G}=\displaystyle \frac{ 3600}{ η_P}$[kJ/kW・h]
$F =\displaystyle \frac{ B}{ P_G}=\displaystyle \frac{ 3600}{ H・η_P}$[kg/kW・h]
$B$[kg/h]:燃料消費量
$H$[kJ/kg]:燃料の発熱量
$P_G$[kW]:発電機出力
$η_P$:発電端熱効率[小数]
$η_P=\displaystyle \frac{ 3600P_G}{ BH}$
設備利用率
設備利用率とは、一定の期間中に得られた発電量(発電機出力 )が、その発電設備が同期間中に100%の出力で発電し続けた場合に占める割合です。
設備利用率を求める式
設備利用率 $ =\displaystyle \frac{ 発電機出力 }{ 最大発電電力量}×100$[%]
排熱回収方式のコンバインドサイクルの効率
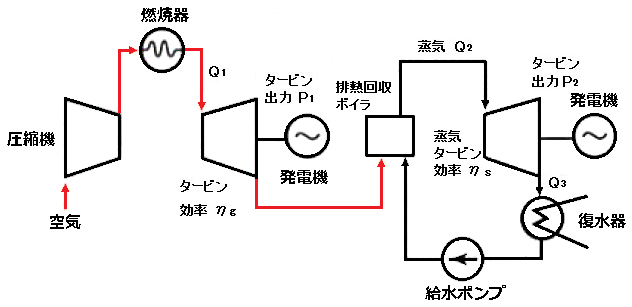
排熱回収コンバインドサイクルの入力熱量は、ガスタービン入口熱量の Q1 [kJ]のみです。廃熱を回収した蒸気の熱エネルギーを Q2[kJ]、蒸気タービンの排気熱量を Q3[kJ]、各タービンの機械的出力を P1、P2[kJ]とすると、ガスタービン効率 ηg と蒸気タービン効率 ηs は、
$η_g=\displaystyle \frac{ P_1}{Q_1}$、$η_s=\displaystyle \frac{ P_2}{Q_2}$
となります。排熱回収方式のコンバインドサイクル全体としての効率を η とすると、
$\begin{eqnarray}η&=&\displaystyle \frac{ P_1+P_2}{Q_1}\\\\&=&\displaystyle \frac{ P_1}{Q_1}+\displaystyle \frac{ Q_2}{Q_1}×\displaystyle \frac{ P_2}{Q_2}\\\\&=&\displaystyle \frac{ P_1}{Q_1}+\displaystyle \frac{ Q_1-P_1}{Q_1}×\displaystyle \frac{ P_2}{Q_2}\\\\&=&\displaystyle \frac{ P_1}{Q_1}+\left(1-\displaystyle \frac{ P_1}{Q_1}\right)×\displaystyle \frac{ P_2}{Q_2}\\\\&=&η_g+(1-η_g)η_s\end{eqnarray}$
排熱回収方式のコンバインドサイクルの効率 η を求める式
$η=η_g+(1-η_g)η_s$
公式集
燃料の保有熱量
$B・H$
汽力発電機の熱効率 η
$η=\displaystyle \frac{ 3600P_T}{ BH}×100$[%]
ボイラ効率 ηB
$η_B=\displaystyle \frac{ Z(i_s-i_w) }{ BH}×100$[%]
熱サイクルの効率 ηC
$η_C=\displaystyle \frac{ (i_s-i_e) }{ (i_s-i_w) }×100$
タービン効率 ηT
$η_T=\displaystyle \frac{ 3600P_T}{ Z(i_s-i_e)}×100$[%]
タービン室効率 ηTR
$η{TR}=\displaystyle \frac{ 3600P_T}{ Z(i_s-i_w)}×100$[%]
発電端熱効率 ηP
$η_P=\displaystyle \frac{ 3600P_G}{ BH}×100$[%]
$η_P=η_Bη{TR}η_G$[%]
発電機効率 ηG
$η_G=\displaystyle \frac{ P_G}{ P_T}×100$[%]
送電端熱効率 ηS
$η_S=\displaystyle \frac{ 3600P_S}{ BH}×100$[%]
$η_S=η_P(1-L)$
所内率 L
$L=1-\displaystyle \frac{ P_S}{ P_G}$
熱消費率 J
$J =\displaystyle \frac{ BH}{ P_G}=\displaystyle \frac{ 3600}{ η_P}$[kJ/kW・h]
燃料消費率 F
$F =\displaystyle \frac{ B}{ P_G}=\displaystyle \frac{ 3600}{ H・η_P}$[kg/kW・h]
設備利用率
設備利用率$=\displaystyle \frac{ 発電機出力 }{ 最大発電電力量}×100$[%]
排熱回収方式のコンバインドサイクルの効率
$η=η_g+(1-η_g)η_s$
電験三種-電力(火力発電)過去問題
1999年(平成11年)問3
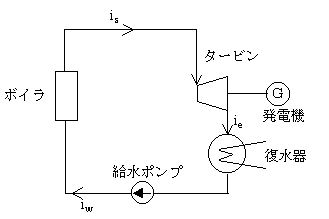
図は汽力発電の熱サイクルを示したものである。このサイクルの熱効率を表す式として、正しいのは次のうちどれか。ただし、iw,is,ieはそれぞれの箇所のエンタルピー[J/kg]を表す。また、ボイラ、タービン、復水器以外でのエンタルピーの増減は無視するものとする。
(1) $\displaystyle \frac{ i_s-i_e }{ i_s-i_w }$ (2) $\displaystyle \frac{ i_s-i_e }{ i_e-i_w }$ (3) $\displaystyle \frac{ i_s-i_w }{ i_s-i_e }$ (4) $\displaystyle \frac{ i_e-i_w }{ i_s-i_e }$ (5) $\displaystyle \frac{ i_e-i_w }{ i_s-i_w }$
1999年(平成11年)問3 過去問解説
熱サイクルの効率を ηC、ボイラ入口給水の比エンタルピーを iw[kJ/kg]、ボイラ出口蒸気の比エンタルピーを is[kJ/kg]、タービン排気の比エンタルピーを ie[kJ/kg]とすると、
$η_C=\displaystyle \frac{ (i_s-i_e) }{ (i_s-i_w) }×100$[%]
答え(1)
2000年(平成12年)問11
最大出力 5,000[kW]の自家用汽力発電所がある。発熱量 44,000[kJ/kg]の重油を使用して50日間連続運転した。この間の重油使用量は 1,200[t]、設備利用率は 60[%]であった。次の(a)及び(b)に答よ。
(a) 発電電力量[MW・h]の値として、正しいのは次のうちどれか。
(1) 1200 (2) 1800 (3) 2160 (4) 3600 (5) 6000
(b) 発電端における熱効率[%]の値として、正しいのは次のうちどれか。
(1) 24.5 (2) 26.5 (3) 28.5 (4) 30.5 (5) 32.5
2000年(平成12年)問11 過去問解説
(a) 発電電力量を P[MW・h]とすると、
$設備利用率=\displaystyle \frac{ 発電電力量}{ 最大発電電力量}×100$[%]
$60=\displaystyle \frac{ P}{ 5000[kW]×50[日]×24[h]}×100$[%]
$P=3600$[MW・h]
答え (4)
(b) 発電端熱効率を ηP、燃料消費量を B[kg/h]、燃料の発熱量を H[kJ/kg]、発電機出力を PG[kW]とすると、
$η_P=\displaystyle \frac{ 3600P_G}{ BH}×100=\displaystyle \frac{ 3600×3600×10^3}{ 44000×1200×10^3}=24.5$[%]
答え (1)
2001年(平成13年)問11
汽力発電設備があり、発電機出力が 18[MW]、タービン出力が 20[MW]、使用蒸気量が 80[t/h]、蒸気タービン入口における蒸気の比エンタルピーが 3,550[kJ/kg]、復水器入口における蒸気の比エンタルピーが2,450[kJ/kg]で運転しているとき、次の(a)及び(b)に答よ。
(a) 発電機効率[%]の値として、正しいのは次のうちどれか。
(1) 74 (2) 85 (3) 90 (4) 95 (5) 98
(b) タービン効率[%]の値として、最も近いのは次のうちどれか。
(1) 69 (2) 82 (3) 85 (4) 87 (5) 90
2001年(平成13年)問11 過去問解説
(a) 発電機効率を ηG、タービン出力を PT[kW]、発電機出力を PG[kW]とすると
$η_G=\displaystyle \frac{ P_G}{ P_T}×100=\displaystyle \frac{ 18}{ 20}×100=90$[%]
答え (3)
(b) 発電機効率を$η_T$、蒸気・給水の流量を Z[kg/h]、ボイラ出口蒸気の比エンタルピーを is[kJ/kg]、タービン排気の比エンタルピーを ie[kJ/kg]、タービン出力を PT[kW]とすると、
$η_T=\displaystyle \frac{ 3600P_T}{ Z(i_s-i_e)}×100$[%]
$η_T=\displaystyle \frac{ 3600×20×10^3}{ 80×10^3×(3550-2450)}×100=82$[%]
答え (2)
2003年(平成15年)問15
出力 700[MW]で運転している汽力発電所で、発熱量 26,000[kJ/kg]の石炭を毎時 230[t]使用している。タービン室効率 47.0[%]、発電機効率 99.0[%]であるとき、次の(a)及び(b)に答よ。
(a) 発電端熱効率[%]の値として、最も近いのは次のうちどれか。
(1) 39.6 (2) 42.1 (3) 44.3 (4) 46.5 (5) 47.5
(b) ボイラ効率[%]の値として、最も近いのは次のうちどれか。
(1) 83.4 (2) 85.1 (3) 88.6 (4) 89.6 (5) 90.6
2003年(平成15年)問15 過去問解説
(a) 発電端熱効率を ηP、燃料消費量を B[kg/h]、燃料の発熱量を H[kJ/kg]、発電機出力を PG[kW]とすると、
$η_P=\displaystyle \frac{ 3600P_G}{ BH}×100$[%]
$η_P=\displaystyle \frac{ 3600×700×10^3}{ 26000×230×10^3}×100=42.1$[%]
答え (2)
(b) ボイラ効率を ηB、タービン室効率を ηTR、発電機効率を ηG とすると、
発電端熱効率 $η_P=η_Bη_{TR}η_G$[%]より
$η_B=\displaystyle \frac{0.421 }{ 0.47×0.99}×100=90.6$[%]
答え (5)
2004年(平成16年)問3
排熱回収方式のコンバインドサイクル発電所が定格出力で運転している。そのときのガスタービン発電効率が ηg、ガスタービンの排気の保有する熱量に対する蒸気タービン発電効率が ηsであった。このコンバインドサイクル発電全体の効率を表わす式として、正しいのは次のうちどれか。
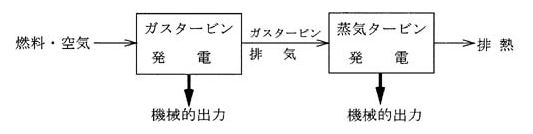
- ηg+ηs
- ηs+(1-ηg)ηg
- ηs+(1-ηg)ηs
- ηg+(1-ηg)ηs
- ηg+(1-ηs)ηg
2004年(平成16年)問3 過去問解説
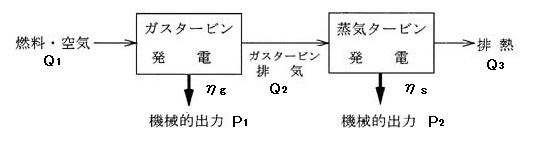
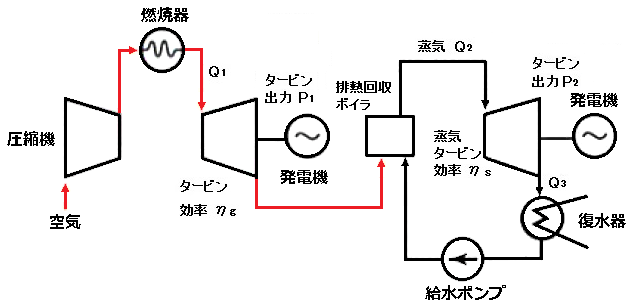
図のように、各熱エネルギーを Q1,Q2,Q3[kJ]、各機械的出力を P1,P2[kJ]とすると、ガスタービン効率 ηg と蒸気タービン効率 ηs は、
$η_g=\displaystyle \frac{ P_1}{Q_1}$
$η_s=\displaystyle \frac{ P_2}{Q_2}$
排熱回収方式のコンバインドサイクル発電所全体の効率を η は、
$\begin{eqnarray}η&=&\displaystyle \frac{ P_1+P_2}{Q_1}\\\\&=&\displaystyle \frac{ P_1}{Q_1}+\displaystyle \frac{ Q_2}{Q_1}×\displaystyle \frac{ P_2}{Q_2}\\\\&=&\displaystyle \frac{ P_1}{Q_1}+\displaystyle \frac{ Q_1-P_1}{Q_1}×\displaystyle \frac{ P_2}{Q_2}\\\\&=&\displaystyle \frac{ P_1}{Q_1}+\left(1-\displaystyle \frac{ P_1}{Q_1}\right)×\displaystyle \frac{ P_2}{Q_2}\\\\&=&η_g+(1-η_g)η_s\end{eqnarray}$
答え (4)
2004年(平成16年)問15
出力 125[MW]の火力発電所が 60日間運転したとき、発熱量 36000[kJ/kg]の燃料油を 24000[t]消費した。この間の発電所の熱効率が 30[%]、所内率が 3[%]であるとき、次の(a)及び(b)に答よ。
(a) 設備利用率[%]の値として、最も近いのは次のうちどれか。
(1) 20 (2) 25 (3) 35 (4) 40 (5) 65
(b) 送電端電力量[MWh]の値として、最も近いのは次のうちどれか。
(1) 66000 (2) 69800 (3) 72000 (4) 74200 (5) 78000
2004年(平成16年)問15 過去問解説
(a) 60日間の最大発電電力量を Wmax、発電端熱効率を ηP、燃料消費量を B[kg/h]、燃料の発熱量を H[kJ/kg]発電機出力を PG とすると、
$W_{max}=125×10^3×60×24=1.8×10^8$[kW・h]
$η_P=\displaystyle \frac{ 3600P_G}{ BH}×100$[%]
$30=\displaystyle \frac{ 3600P_G}{ 24000×10^3×36000}×100$
$P_G=7.2×10^7$[kW・h]
設備利用率$=\displaystyle \frac{ 発電機出力}{ 最大発電電力量}×100=\displaystyle \frac{ 7.2×10^7}{ 1.8×10^8}×100≒40$[%]
答え (4)
(b) 所内率を L、送電端電力を PS とすると
$L=1-\displaystyle \frac{ P_S}{ P_G}$
$0.03=1-\displaystyle \frac{ P_S}{ 7.2×10^7}$
$P_S=69800$[MWh]
答え (2)
2007年(平成19年)問2
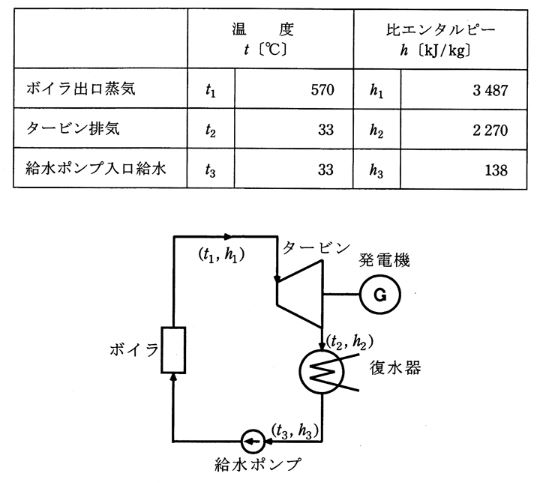
ある汽力発電所において、各部の汽水の温度及び単位質量当たりのエンタルピー(これを「比エンタルピー」という。)[kJ/kg]が、下表の値であるとき、このランキンサイクルの効率[%]の値として、最も近いのは次のうちどれか。
ただし、ボイラ、タービン、復水器以外での温度及びエンタルピーの増減は無視するものとする。
(1) 34.9 (2) 36.3 (3) 39.1 (4) 43.3 (5) 53.6
2007年(平成19年)問2 過去問解説
ランキンサイクルの効率を ηC、ボイラ入口給水の比エンタルピーを h3[kJ/kg]、ボイラ出口蒸気の比エンタルピーを h1[kJ/kg]、タービン排気の比エンタルピーを h2[kJ/kg]とすると、
$η_C=\displaystyle \frac{ (h_1-h_2) }{ (h_1-h_3) }×100$
$η_C=\displaystyle \frac{ (3487-2270) }{ (3487-138) }×100=36.3$[%]
答え (2)
2008年(平成20年)問15
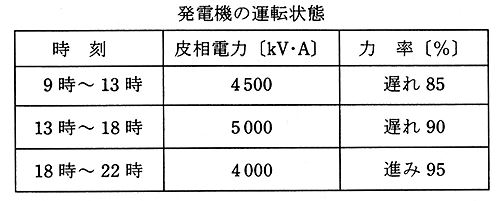
汽力発電所において、定格容量 5000[kV・A]の発電機が 9時から 22時の間に下表に示すような運転を行ったとき、発熱量 44000[kJ/kg]の重油を 14[t]消費した。この9時から 22時の間の運転について、次の(a)及び(b)に答よ。
ただし、所内率は 5[%]とする。
(a) 発電機の発電電力[MW・h]の値として、正しいのは次のうちどれか。
(1) 12 (2) 23 (3) 38 (4) 53 (5) 59
(b) 送電端熱効率[%]の値として、最も近いのは次のうちどれか。
(1) 28.8 (2) 29.4 (3) 31.0 (4) 31.6 (5) 32.2
2008年(平成20年)問15 過去問解説
(a) 発電機出力を PG[kW・h]は、
PG=(4500×0.85×4)+(5000×0.90×5)+(4000×0.95×4)=53000[kW・h]
答え (4)
(b) 送電端熱効率を ηS、発電端熱効率を ηP、所内率を L とすると、
ηS=ηP(1-L)=0.31(1-0.05)=0.2945
答え (2)
2010年(平成22年)問15
最大発電電力量 600[MW]の石炭火力発電がある。石炭の発熱量を 26400[kJ/kg]として、次の(a)及び(b)に答えよ。
(a) 日負荷率 95.0[%]で 24時間運転したとき、石炭の消費量は 4400[t]であった。発電端熱効率[%]の値として、最も近いのは次のうちどれか。
なお、日負荷率[%]=(平均発電電力/最大発電電力量)×100 とする。
(1) 37.9 (2) 40.2 (3) 42.4 (4) 44.6 (5) 46.9
(b) タービン効率 45.0[%]、発電機効率 99.0[%]、所内比率 3.00[%]とすると、発電端効率が 40.0[%]のときのボイラ効率[%]の値として、最も近いのは次のうちどれか。
(1) 40.4 (2) 73.5 (3) 87.1 (4) 89.8 (5) 92.5
2010年(平成22年)問15 過去問解説
(a) 平均発電電力 Pg は、
日負荷率[%]$=\displaystyle \frac{ 平均発電電力 }{ 最大発電電力量 }×100$
$0.95=\displaystyle \frac{ P_G }{ 600×10^3 }$
$P_g =570×10^3 $ [kW/日]
発電端熱効率を ηP、燃料消費量を B[kg/h]、燃料の発熱量を H[kJ/kg]、発電機出力を PG[kW]とすると、
$η_P=\displaystyle \frac{ 3600P_G}{ BH}×100$[%]
$=\displaystyle \frac{ 3600×570×10^3×24}{ 4400×10^3×26400}×100=42.4$[%]
答え (3)
(b) ボイラ効率を ηB、タービン室効率を ηTR、発電機効率を ηG とすると、
発電端熱効率 ηP=ηBηTRηG より
0.40=ηB×0.45×0.99
ηB=0.898
答え (4)
2012年(平成24年)問15
定格出力 300[MW]の石炭火力発電所について、次の(a)及び(b)の問に答えよ。
(a) 定格出力で 30日間連続運転したときの送電端電力量[MW・h]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、所内率は 5[%]とする。
(1) 184000 (2) 194000 (3) 205000 (4) 216000 (5) 227000
(b) 1日の間に下表に示すような運転を行ったとき、発熱量 28000[kJ/kg]の石炭を 1700[t] 消費した。この1日の間の発電端熱効率[%]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
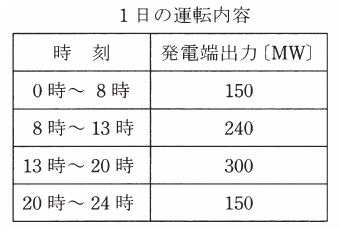
(1) 37.0 (2) 38.5 (3) 40.0 (4) 41.5 (5) 43.0
2012年(平成24年)問15 過去問解説
(a) 30 日間の発電機出力を PG30[MW・h]、送電端電力量を PS30[MW・h]、所内率を L とすると、
$L=1-\displaystyle \frac{ P_{S30}}{ P_{G30}}$
$L=1-\displaystyle \frac{ P_{S30}}{ 300×30×24}=20500$[MW・h]
答え (3)
(b) 1日の発電機出力を PG[kW]とすると、
$P_G=(150×8+240×5+300×7+150×4)×10^3=5100×10^3$
発電端熱効率を ηP、燃料消費量を B[kg/h]、燃料の発熱量を H[kJ/kg]とすると、
$η_P=\displaystyle \frac{ 3600P_G}{ BH}×100$[%]
$η_P=\displaystyle \frac{ 3600×5100×10^3}{ 1700×10^3×28000}×100≒38.5$[%]
答え (2)
2013年(平成25年)問2
排熱回収方式のコンバインドサイクル発電所において、コンバインドサイクル発電の熱効率が 48[%]、ガスタービン発電の排気が保有する熱量に対する蒸気タービン発電の熱効率が 20[%]であった。ガスタービン発電の熱効率[%]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、ガスタービン発電の排気はすべて蒸気タービン発電に供給されるものとする。
(1) 23 (2) 27 (3) 28 (4) 35 (5) 38
2013年(平成25年)問2 過去問解説
ガスタービン効率を ηg 、蒸気タービン効率 ηs とすると、排熱回収方式のコンバインドサイクル発電所全体の効率を η は、
η=ηg+(1-ηg)ηs
0.48=ηg+(1-ηg)×0.2
ηg=0.35
答え (4)
2015年(平成27年)問3
定格出力 10000kW の重油燃焼の汽力発電所がある。この発電所が 30日間連続運転し、そのときの重油使用量は 1100t、送電端電力量は 5000MW・h であった。この汽力発電所のボイラ効率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
なお、重油の発熱量は 44000kJ/kg、タービン室効率は 47%、発電機効率は 98%、所内率は 5%とする。
(1) 51 (2) 77 (3) 80 (4) 85 (5) 95
2015年(平成27年)問3 過去問解説
所内率を L、送電端電力量を PS とすると、発電機出力 PG は、
$L=1-\displaystyle \frac{ P_S}{ P_G}$
$0.05=1-\displaystyle \frac{ 5000×10^3}{ P_G}$
$P_G≒5.26×10^6$[KW・h]
発電端熱効率を ηP、燃料消費量を B[kg/h]、燃料の発熱量を H[kJ/kg]、発電機出力を PG[kW]とすると、
$η_P=\displaystyle \frac{ 3600P_G}{ BH}$
$η_P=\displaystyle \frac{ 3600×5.26×10^6}{ 11000×10^3×44000H}≒0.391 $
ボイラ効率を ηB、タービン室効率を ηTR、発電機効率を ηG とすると、
ηP=ηBηTRηG より、
0.391=ηB×0.47×0.98
ηB= 0.849
答え (4)
2016年(平成28年)問15
図は、あるランキンサイクルによる汽力発電所のP-V線図である。この発電所が、A点の比エンタルピー 140kJ/kg、B点の比エンタルピー 150kJ/kg、C点の比エンタルピー 3380kJ/kg、D点の比エンタルピー 2560kJ/kg、蒸気タービンの使用蒸気量 100t/h、蒸気タービン出力 18MW で運転しているとき、次の(a)及び(b)の問に答えよ。
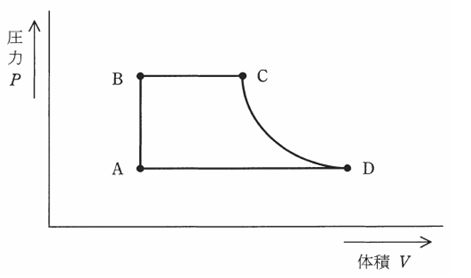
(a) タービン効率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 58.4 (2) 66.8 (3) 79.0 (4) 95.3 (5) 96.7
(b) この発電所の送電端電力 16MW、所内比率 5%のとき、発電機効率の値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1)84.7 (2)88.6 (3)88.9 (4)89.2 (5)93.6
2016年(平成28年)問15 過去問解説
(a) タービン効率を ηT、蒸気・給水の流量を Z[kg/h]、ボイラ出口蒸気の比エンタルピーを is[kJ/kg]、タービン排気の比エンタルピーを ie[kJ/kg]、タービン出力を PT[kW]とすると、
$η_T=\displaystyle \frac{ 3600P_T}{ Z(i_s-i_e)}×100$[%]
$η_T=\displaystyle \frac{ 3600×18×10^3}{ 100×10^3(3380-2560)}×100=79.0$[%]
答え (3)
(b) 所内率 L 、発電機出力 PG 、送電端電力 PS の関係は、
$L=1-\displaystyle \frac{ P_S}{ P_G}$
$0.05=1-\displaystyle \frac{ 16×10^3}{ P_G}$
$P_G=16.84×10^3$[kW]
発電機効率を ηG、タービン出力を PT[kW]、発電機出力 PG[kW]とすると
$η_G=\displaystyle \frac{ P_G}{ P_T}×100=\displaystyle \frac{ 16.84×10^3}{ 18×10^3}×100=93.6$[%]
答え (5)





