第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「クーロンの法則」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「クーロンの法則」の過去問題も解説しています。
電気を帯びた物質の間に働く力
静電気は二つの物質を摩擦することなどによって発生します。静電気などによって物質に電気を帯びることを「帯電」といいます。また、物質が帯びている電気の量を「電荷」といいます。尚、大きさを考えない点状の電荷のことを「点電荷」といいます。
電荷はすべての電気的な現象の元となるものです。電荷には正(プラス)と負(マイナス)の2種類があり、単位はクーロン[C]です。1クーロン[C]は 1アンペア[A]の電流が 1秒間に運ぶ電荷の量です。
帯電(電気を帯びた)した物質間には、力が働きます。この力は引力になるときと、反発力になるときがあります。引力は「物質が互いに引っぱりあう力」、反発力は「物質が互いに離れようとする力」です。
この帯電した物質間に働く力が、引力になるのか、反発力になるのかを決める元になるのが、電荷が持っている電気の符号です。電荷の符号が同符号の場合は反発力、異符号の場合は引力が働きます。このように電荷の間にはたらく力のことを「静電気力」といいます。
静電気力の大きさは2つの電荷の持つ電気量が大きいほど、また電荷間が近いほど大きくなります。
.png)
二つの電荷の符号が同じとき、静電気力は反発力(斥力)となります。
.png)
二つの電荷の符号が異なるとき、静電気力は引力となります。
- 物質が電気を帯びることを帯電といい、帯びている電気の量を電荷といいます。
- 電荷が持つ電気の量の単位はクーロン[C]です。
- 静電気力は同種の電荷の場合は反発力、異種の電荷の場合は引力が働きます。
- 2つの電荷の持つ電気量が大きいほど、静電気力は大きくなります。
- 2つの電荷の距離が近いほど、静電気力は大きくなります。
クーロンの法則
帯電した二つの物質間に働く力の大きさは、それぞれが持つ電荷の積に比例し、距離の2乗に反比例します。これを「クーロンの法則」といいます。
二つの電荷の量をそれぞれ $ Q_{ 1 },Q_{ 2 }$[C]、電荷間の距離を $r$[m]とすると、二つの電荷間に働く力の大きさ $ F$[N]は、次の式で求めることができます。
クーロンの法則
$ F=\displaystyle \frac{ 1 }{ 4πε_{ o } }\frac{ Q_{ 1 }Q_{ 2 } }{ r^2}$[N]
$F$[N]:二つの電荷間に働く力の大きさ
$ ε_{ o }$[F/m]:真空の誘電率
$Q_{ 1 },Q_{ 2 }$[C]:電荷
$r$[m]:電荷間の距離
.png)
$ ε_{ o }$(イプシロンゼロ)は「真空の誘電率」と呼ばれる定数です。誘電率とは、電荷の貯め易さを表わす物理定数です。誘電率が高い物質ほど、電荷を貯め易いといえます。
真空の誘電率は $ ε_{ o }=8.85×10^{-12}$[F/m](ファラド毎メートル)です。空気中でもほぼ同じ値です。計算式で使う場合は、
$ ε_{ o } =\displaystyle \frac{ 1 }{ 4π×9.0×10^9}$[F/m]
を使うと便利です。
二つ以上の電荷の間の静電気力
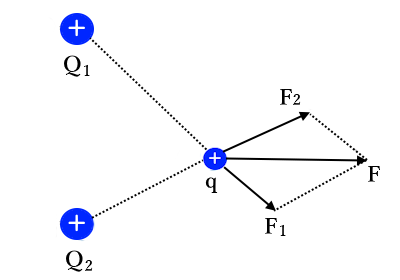
図のように電荷 $q$[C]が二つの電荷 $Q_{ 1 }$[C],$ Q_{ 2 }$[C]から受ける静電気力 $F$[N]の大きさを考えます。ただし、$q$,$Q_{ 1 }$,$Q_{ 2 }$はいずれも正電荷とします。
静電気力は、力学で学ぶ力と同様にベクトルで考えます。したがって、ベクトルの和が合力となります。$q$ が $ Q_{ 1 }$ から受ける静電気力を $ F_{ 1 }$[N]、$ q$ が $ Q_{ 2 }$ から受ける静電気力を $ F_{ 2 }$[N]とすると、静電気力の合力 $F$[N]は、ベクトルの合成より平行四辺形の対角線となります。
電験三種-理論の過去問解説:「静電気分野-クーロンの法則」
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2002年(平成14年)問2【電験理論の過去問題】
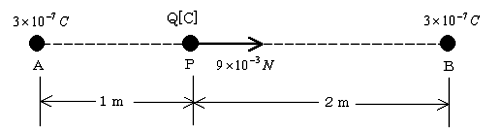
図のように、真空中の 3[m]離れた2点A,Bにそれぞれ 3×10$^{ -7}$[C]の正の点電荷がある。A点とB点とを結ぶ直線上のA点から 1[m]離れたP点に Q[C]の正の点電荷を置いたとき、その点電荷にB点の方向に 9×10$^{-3}$[N]の力が働いた。この点電荷 Q[C]の値として、最も近いのは次のうちどれか。
ただし、真空中の誘電率を $ ε_{ o } =\displaystyle \frac{ 1 }{ 4π×9.0×10^9}$[F/m]とする。
(1) 1.2×10$^{-9}$ (2) 1.8×10$^{-8}$ (3) 2.7×10$^{-7}$ (4) 4.4×10$^{-6}$ (5) 7.3×10$^{-5}$
AP間に働く力を $ F_{ AP }$[N]とすると、クーロンの法則より
$ \begin{eqnarray}F_{ AP }&=&\displaystyle \frac{ 1 }{ 4πε_{ o } }\frac{ Q_{ A }Q_{ P } }{ r_{AP}^2}\\\\&=&9.0×10^9×\displaystyle \frac{ 3×10^{-7}×Q}{ 1^2}\\\\&=&27.0Q×10^2[N]\end{eqnarray}$
BP間に働く力を $ F_{ BP }$[N]とすると、クーロンの法則より
$ \begin{eqnarray}F_{ BP }&=&\displaystyle \frac{ 1 }{ 4πε_{ o } }\frac{ Q_{ B }Q_{ P } }{ r_{BP}^2}\\\\&=&9.0×10^9×\displaystyle \frac{ 3×10^{-7}×Q}{ 2^2}\\\\&=&6.75Q×10^2[N]\end{eqnarray}$
P点に働く力は $F$[N]は、$ F=F_{ AP }-F_{ BP }=9×10^{-3}$[N]なので
$ \begin{eqnarray}F&=&F_{ AP }-F_{ BP }\\\\&=&27.0Q×10^2-6.75Q×10^2\\\\&=&20.25Q×10^2=9×10^{-3}[N]\end{eqnarray}$
$ Q=4.44×10^{-6}$[C]
答え (4)
2003年(平成15年)問15【電験理論の過去問題】
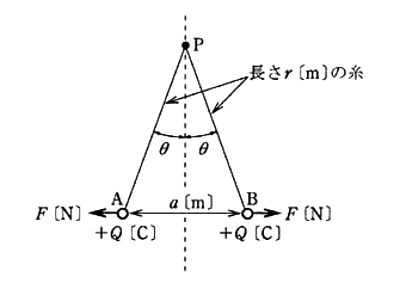
真空中において、それぞれ質量 m[kg]、電荷 +Q[C]の小さな球の帯電体A及びBがある。これらの帯電体をそれぞれ長さ r[m]の糸で点Pからつるしたところ、図のように、帯電体A,Bの間隔が a[m]となって静止した。次の(a)及び(b)に答よ。
ただし、真空の誘電率 $ε_0$[F/m]、重力加速度 g[m/s2]とする。また、帯電体A及びBの直径は r[m]に比べて十分小さく、糸の質量は無視できるものとする。
(a) 帯電体A,B間に働く力 F[N]の大きさとして、正しいものは次のうちどれか。
(1) $\displaystyle \frac{Q}{4πε_oa}$ (2) $\displaystyle \frac{Q}{ 4πε_oa^2}$ (3) $\displaystyle \frac{Q^2}{ 2πε_oa}$ (4) $\displaystyle \frac{ Q^2 }{ 2πε_oa^2}$ (5) $\displaystyle \frac{ Q^2 }{ 4πε_oa^2}$
(b) 帯電体A、B間の静止状態において、糸の鉛直直線に対する傾きが θ[°]であったときに成立する式として、正しいのは次のうちどれか。
(1) $Q^2=16πε_{ o } mgr^2 sin^2θtanθ$
(2) $Q^2=\displaystyle\frac{16πε_{ o } mgr^2 sin^2θ}{tanθ}$
(3) $Q^2=\displaystyle\frac{16πε_{ o } mgr^2 cos^3θ}{sinθ}$
(4) $Q^2=8πε_{ o } mgr^2 sin^2θtanθ$
(5) $Q^2=8πε_{ o } mgr^2 sinθcosθ$
(a) AB間に働く力を F[N]は、クーロンの法則より、
$ F=\displaystyle \frac{ 1 }{ 4πε_{ o } }\frac{ Q_{ A }Q_{ B } }{ r_{AB}^2}=\displaystyle \frac{ Q^2 }{ 4πε_{ o } a^2}$
答え (5)
(b) 静止状態に働く力を図示します。
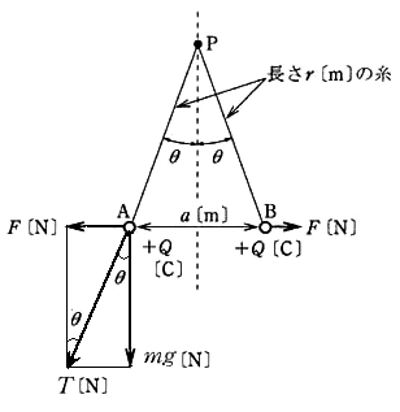
力の関係は、
$ T=\displaystyle \frac{ mg }{ cosθ }=\displaystyle\frac{ F}{sinθ}$
(a)の解を代入すると、
$\displaystyle \frac{ mg }{ cosθ }=\displaystyle\frac{ \displaystyle \frac{ Q^2 }{ 4πε_{ o } a^2}}{sinθ}$
$Q^2=\displaystyle \frac{ 4πε_{ o } a^2mg sinθ}{ cosθ }$
三角関数より、$sinθ=\displaystyle \frac{\displaystyle \frac{a}{ 2 } }{ r }$ なので、
$\begin{eqnarray}Q^2&=&\displaystyle \frac{ 4πε_{ o } (2rsinθ)^2mg sinθ}{ cosθ }\\\\&=&16πε_{ o } mgr^2 sin^2θtanθ\end{eqnarray}$
答え (1)
2005年(平成17年)問1【電験理論の過去問題】
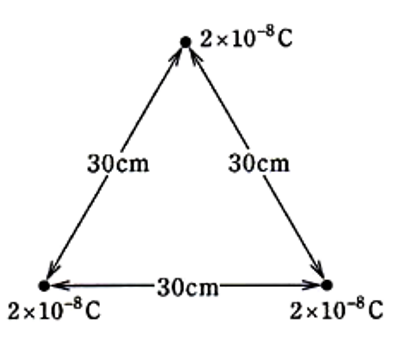
真空中において、図に示すように一辺の長さが 30[cm]の正三角形の各頂点に 2×10$^{-8}$[C]の正の点電荷がある。この場合、各点電荷に働く力の大きさ F[N]の値として、最も近いのは次のうちどれか。
ただし、真空中の誘電率を $ ε_{ o } =\displaystyle \frac{ 1 }{ 4π×9.0×10^9}$[F/m]とする。
(1) 6.92×10$^{-5}$ (2) 4.00×10$^{-5}$ (3) 3.46×10$^{-5}$ (4) 2.08×10$^{-5}$ (5) 1.20×10$^{-5}$
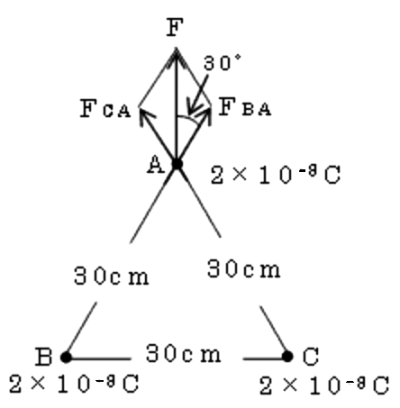
点電荷A,B,Cに働く力は同じですので、点電荷Aに働く力について考えます。点電荷AC間に働く力を $ F_{ CA } $[N]、点電荷AB間に働く力 $F_{ BA } $[N]とすると、$ F_{CA} =F_{BA}$[N]が成り立ちます。
ここで $ F_{ CA }$[N]と $F_{ BA }$[N]がつくる合成力 $F$[N]は
$ F=F_{ CA } ×cos30°×2$[N]
クーロンの法則より
$ \begin{eqnarray}F_{ CA } &=&\displaystyle \frac{ 1 }{ 4πε_{ o } }\frac{ Q_{ C }Q_{ A } }{ r_{ CA }^2}\\&=& 9.0×10^9×\displaystyle\frac{ (2×10^{ -8})^2 }{ (0.3)^2}\\&=&4×10^{ -5}\end{eqnarray}$
したがって、
$ \begin{eqnarray}F&=&4×10^{ -5} ×cos30°×2\\&=&4×10^{ -5} ×\frac{ \sqrt{ 3 } }{ 2 }×2\\&=&6.92×10^{ -5}[N]\end{eqnarray}$
答え (1)
2013年(平成25年)問2【電験理論の過去問題】
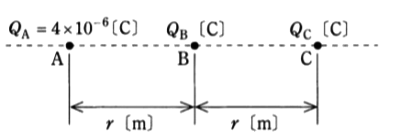
図のように真空中の直線上に間隔 $r$[m]を隔てて、点 A,B,Cがあり、各点に電気量 $ Q_A=4×10^{ -6}$[C],$Q_B$[C],$Q_C$[C]の点電荷を置いた。これら三つの点電荷に働く力がそれぞれ零になった。このとき、$Q_B$[C]及び $Q_C$[C]の値の組み合わせとして、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、真空中の誘電率を $ ε_{ o } =\displaystyle \frac{ 1 }{ 4π×9.0×10^9}$[F/m]とする。

A,B,Cの各点に働く力を $ F_{ AB }$[N],$ F_{ AC }$[N],$ F_{ BC }$[N]、$ \displaystyle \frac{ 1 }{ 4πε_{ o } }=k$ とすると、クーロンの法則より、
$ F_{ AB }=k\displaystyle \frac{Q_{ A }Q_{ B } }{ r^2}$[N]
$ F_{ AC }=k\displaystyle \frac{Q_{ A }Q_{ C } }{ (2r)^2}$[N]
$ F_{ BC }=k\displaystyle \frac{Q_{ B }Q_{ C } }{ r^2}$[N]
題意より、$ F_{ AB }= F_{ AC }$[N]なので、
$ k\displaystyle \frac{Q_{ A }Q_{ B } }{ r^2}=k\displaystyle \frac{Q_{ A }Q_{ C } }{ (2r)^2}$
$ Q_{ A }Q_{ B } = \displaystyle\frac{1}{ 4 }Q_{ A }Q_{ C } $
$ Q_{ B } = \displaystyle\frac{1}{ 4 }Q_{ C } $
題意より、$ F_{ AB }= F_{ BC }$[N]なので
$ k\displaystyle \frac{Q_{ A }Q_{ B } }{ r^2}=k\displaystyle \frac{Q_{ B }Q_{ C } }{ r^2}$
$ Q_{ A }Q_{ B } = Q_{ B }Q_{ C } $
$ Q_{ A } = Q_{ C } $
力の向きを考えてみると、$ Q_{ A }$は+の電荷なので、図から判断すると、$ Q_{ C }$は+の電荷、$ Q_{ B }$は-の電荷になります。
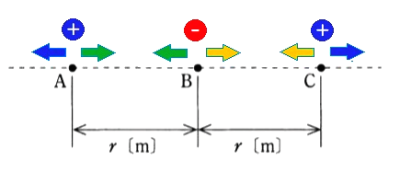
よって、
$ Q_{ B } = -1×10^ { -6 }$
$ Q_{ C } = 4×10^ { -6 }$
答え (3)
電験三種の理論科目に出題される「静電気分野」のページ
1.クーロンの法則とは
2.電界とガウスの法則
3.静電界中の電位と電圧
4.静電誘導と誘電分極
5.平行平板コンデンサの静電容量
6.コンデンサの直列接続と並列接続
7.静電エネルギー
8.誘電体とコンデンサ
9.導体球と同心球導体の静電容量






