電験3種の計算問題で使う数学は、中学校から高校2年生までに習う数学の範囲で十分に対応ができます。電験3種の問題をはじめる前に、まずは数学の計算問題をおさらいしましょう。基礎知識がなければ電験3種には太刀打ち出来ません。このページでは基礎となる中学で習う範囲から、電験3種の数学で必要な個所のみをピックアップし、説明しています。
四則計算について
まずは計算式に登場する言葉の意味と計算のルールについて、理解しましょう。電験3種の試験には言葉の意味は出てきませんが、数学の勉強をするのに必要となってきます。計算のルールは重要ですので、必ずマスターしてください。
四則計算に登場する用語
- 単項式
$ 2x$、$ ax^2$、$ abx$ などのように、数や文字についての乗法だけで作られている式です。
- 多項式
$ 2x+ax^2$、$ 2x+abx$ などのように、いくつかの単項式を加えた式です。
- 係数
文字を含む単項式の数の部分です。$ 2x$の係数は$ 2$、$ a$の係数は$ 1$となります。
- 次数
かけられている文字の個数のことです。$ 2ab$という単項式なら、$ 2$という数字に文字$ a$と文字$ b$が掛けられているので、次数は2となります。$ 2x^2y$という単項式なら、$ x$が2回(2乗なので)と$ y$が1回 $ 2$に掛けられているので、次数は$ 3$となります。
- 同類項
文字の部分が全く同じ項のことです。多項式 $ 2x+ ax^2+6x$ の $ 2x$と $ 6x$ は同類項です。
四則計算のルール
四則とは、加算(足し算)、減算(引き算)、乗算(かけ算)、除算(割り算)のことで、これらの4つの計算のことを四則計算といいます。この四則計算には計算を行う順番のルールがあります。
- (カッコ)の中を計算する。
- 累乗(2乗とか3乗とか)を計算する。
- 割り算・かけ算の計算をする。
- 足し算・引き算の計算をする。
このルール通りに四則計算を守らないと答えが違ってきます。
例えば 「$ 4×5-10÷2=$」 を前から順番に計算すれば、
$ 4×5-10÷2$
$ =20-10÷2$
$ =10÷2$
$=5$
となり、この答えは間違いです。正しくは、
$ 4×5-10÷2$
$ =20-5$
$ =15$
となります。このように四則計算のルールはとても大事ですので、確認をしておいてください。
四則計算の法則
四則計算には、いくつか法則や公式があります。これらは自由自在に使いこなせるようにしておいて下さい。
加法・減法の計算の法則
- 交換の法則
$ a+b=b+a$
- 結合の法則
$ (a+b)+c=a+(b+c)$
乗法の計算の法則
- 交換の法則
$ a×b=b×a$
- 結合の法則
$ (a×b)×c=a×(b×c)$
- 分配の法則
$ (a+b)×c=a×c+b×c$
多項式の展開方法
多項式と多項式の積を展開するには、次のようにかけあわせます。
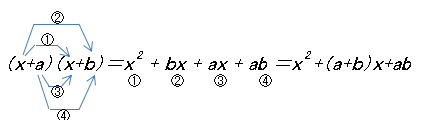
乗法の公式
$ (x+y)^2$
$ =x^2+2xy+y^2$
$ (x-y)^2$
$ =x^2-2xy+y^2$
$ (x+y)(x-y)$
$ =x^2-y^2$
$ (x+a)(x+b)$
$ =x^2+(a+b)x+ab$
$ (ax+b)(cx+d)$
$ =acx^2+(ad+bc)x+bd$
演習問題1
次の計算ができますか?
1. $ 3(5-x)=$
2. $ 2(4-3x)-3(3x+1)=$
3. $ (2x+5y)^2=$
4. $ 6(x^2+2x)-3(x^2-4x)=$
5. $ (x+2)(3x-5)=$
演習問題1の解答
1の解答
$ 3(5-x)=15-3x$
2の解答
$2(4-3x)-3(3x+1)$
$=8-6x-9x-3$
$= 5-15x$
3の解答
$ (2x+5y)^2$
$ =(2x)^2+2×2x×5y+(5y)^2$
$ =4x^2+20xy+25y^2$
4の解答
$ 6(x^2+2x)-3(x^2-4x)$
$ =6x^2+12x-3x^2+12x$
$ =6x^2-3x^2+12x+12x$
$ =3x^2+24x$
5の解答
$ (x+2)(3x-5)$
$ =3x^2-5x+6x-10$
$ =3x^2+x-10$
一次方程式
方程式とは、「未知数を表す文字を含む等式」です。簡単に言えば「まだわかっていない数がある式がイコールで結ばれている計算式」です。この式が、1次の項と定数の項で成り立っているものを一次方程式といいます。
等式の性質
(1)等式は、その両辺に同じ数を加減しても、等式は成立します。
A=B ⇒ A+C=B+C
A=B ⇒ A−C=B−C
$ x-3=2$
⇒ $ x-3\color{red}{+3}=2\color{red}{+3}$
⇒ $ x=5$ ・・・ 答え
$ x+3=5$
⇒ $ x+3\color{red}{-3}=5\color{red}{-3}$
⇒ $ x=2$ ・・・ 答え
(2)等式は、その両辺に同じ数を乗除しても、等式は成立します。
A=B ⇒ A×C=B×C
A=B ⇒ A÷C=B÷C
$ \displaystyle \frac{x}{2}=8$
⇒ $ \displaystyle \frac{x}{2}\color{red}{×2}=8\color{red}{×2}$
⇒ $ x=16$ ・・・ 答え
$ 2x=8$
⇒ $ \displaystyle 2x×\frac{\color{red}1}{\color{red}2}=8×\frac{\color{red}1}{\color{red}2}$
⇒ $ x=4$ ・・・ 答え
xが両辺にある1次方程式
(1)xを含む項を左辺に集め、定数項を右辺に集めるように変形します。
$ 5x−2=3x+4$ の解は
$ 5x−3x−2=4$
$ 2x−2=4$
$ 2x=4+2$
$ 2x=6$
$ x=3$ ・・・ 答え
演習問題2
次の計算ができますか?
1. $ -3x-6=0$
2. $ 20x+20=30x-100$
3. $ 0.14+0.21y=0.28y-0.07$
4. $ \displaystyle \frac{5x-4}{4}=\frac{x+7}{2}$
5. $ 4(x-0.7)-1.4=3.3x$
演習問題2の解答
1の解答
$ -3x-6=0$
$ -3x=6$
$ x=-2$
2の解答
$ 20x+20=30x-100$
$ 20x-30x=-100-20$
$ -10x=-120$
$ x=12$
3の解答
$ 0.14+0.21y=0.28y-0.07$
すべて100倍します。
$ 14+21y=28y-7$
$ 21y-28y=-7-14$
$ -7y=-21$
$ y=3$
4の解答
$ \displaystyle \frac{5x-4}{4}=\frac{x+7}{2}$
$ \displaystyle 4×\frac{5x-4}{4}=4×\frac{x+7}{2}$
$ 5x-4=2×(x+7)$
$ 5x-4=2x+14$
$ 5x-2x=14+4$
$ 3x=18$
$ x=6$
5の解答
$ 4(x-0.7)-1.4=3.3x$
$ 4x-2.8-1.4=3.3x$
$ 4x-3.3x=2.8+1.4$
$ 0.7x=4.2$
$ x=6$
連立方程式
連立方程式の解き方の基本は,1つの文字を消去してもう1つの文字だけの方程式にすることです。
代入法による解き方
一方の式を他方に代入することで連立方程式を解くことができます。
$ \begin{eqnarray} \left\{ \begin{array}{l} 6x-3y=6 ・・・ ①\\ y-x=1 ・・・ ②\end{array} \right.\end{eqnarray}$
②式を変形する
$ y=x+1$ ・・・ ③
③式を①に代入する
$ 6x-3(x+1)=6$
$ 6x-3x-3=6$
$ x=3$ ・・・ ④
④式を③に代入する
$ y=3+1=4$
$ x=3、y=4$ ・・・ 答え
加減法による解き方
加減法は、2つの方程式を足したり引いたりすることによって文字を消去し、方程式を解く方法です。
$ \begin{eqnarray} \left\{ \begin{array}{l} 6x-y=12 ・・・ ①\\ x-y=2 ・・・ ②\end{array} \right.\end{eqnarray}$
①式から②式を引きます。
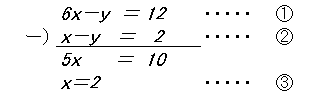
③式を②式に代入します。
$ 2-y=2$
$ y=0$
$ x=2、y=0$ ・・・ 答え
演習問題3
次の計算ができますか?
1. $ \begin{eqnarray} \left\{ \begin{array}{l} 6x-y=12\\ x-y=2\end{array} \right.\end{eqnarray}$
2. $ \begin{eqnarray} \left\{ \begin{array}{l} 3x=-4y-6\\ 3x+5y=-9\end{array} \right.\end{eqnarray}$
3. $ \begin{eqnarray} \left\{ \begin{array}{l} 0.7x+y=2.6\\ 0.08x-0.2y=1.24\end{array} \right.\end{eqnarray}$
4. $ \begin{eqnarray} \left\{ \begin{array}{l} \displaystyle\frac{x}{4}=\frac{2y}{5}+4\\ \displaystyle\frac{y}{5}+\frac{x}{4}=-20\end{array} \right.\end{eqnarray}$
5. $ \begin{eqnarray} \left\{ \begin{array}{l} ax+by=7\\ bx+2ay=4\end{array} \right.\end{eqnarray}$
の解が$ x=2, y=1$ のとき、$ a, b$ の値はいくらですか?
演習問題3の解答
1の解答
$ \begin{eqnarray} \left\{ \begin{array}{l} 6x-y=12 ・・・ ①\\ x-y=2 ・・・ ②\end{array} \right.\end{eqnarray}$
①式から②式を引きます
5x=10$
$ x=2$ ・・・ ③
③式を②式に代入します
$ 2-y=2$
$ y=0$
$ x=2,y=0$ (答え)
2の解答
$ \begin{eqnarray} \left\{ \begin{array}{l} 3x=-4y-6\\ 3x+5y=-9\end{array} \right.\end{eqnarray}$
上式を変形します
$ \begin{eqnarray} \left\{ \begin{array}{l} 3x+4y=-6 ・・・ ①\\ 3x+5y=-9 ・・・ ②\end{array} \right.\end{eqnarray}$
①式から②式を引きます
$ -y=3$
$ y=-3$ ・・・ ③
③式を②式に代入します
$ 3x+5×(-3)=-9$
$ 3x=-9+15$
$ 3x=6$
$ x=2$
$ x=2,y=-3$(答え)
3の解答
$ \begin{eqnarray} \left\{ \begin{array}{l} 0.7x+y=2.6\\ 0.08x-0.2y=1.24\end{array} \right.\end{eqnarray}$
上式を変形します
$ \begin{eqnarray} \left\{ \begin{array}{l} y=-0.7x+2.6 ・・・ ①\\ 0.08x-0.2y=1.24 ・・・ ②\end{array} \right.\end{eqnarray}$
①式を②式に代入します
$ 0.08x-0.2×(-0.7x+2.6)=1.24$
$ 0.08x+0.14x-0.52=1.24$
$ 0.22x=1.76$
$ x=8$ ・・・ ③
③式を①式に代入します
$ y=-0.7×8+2.6$
$ y=-5.6+2.6=-3$
$ x=8,y=-3$ (答え)
4の解答
$ \begin{eqnarray} \left\{ \begin{array}{l} \displaystyle\frac{x}{4}=\frac{2y}{5}+4 ・・・ ①\\ \displaystyle\frac{y}{5}+\frac{x}{4}=-20 ・・・ ②\end{array} \right.\end{eqnarray}$
①式を②式に代入します
$ \displaystyle\frac{y}{5}+\frac{2y}{5}+4=-20$
$ \displaystyle\frac{3y}{5}=-24$
$ y=-24×\displaystyle\frac{5}{3}$
$ y=-40$ ・・・ ③
③式を①式に代入します
$ \displaystyle\frac{x}{4}=\frac{2×(-40)}{5}+4$
$ \displaystyle\frac{x}{4}=(-16)+4$
$ x=-48$
$ x=-48,y=-40$ (答え)
5の解答
$ \begin{eqnarray} \left\{ \begin{array}{l} ax+by=7\\ bx+2ay=4\end{array} \right.\end{eqnarray}$
の解が$ x=2, y=1$ のとき、$ a, b$ の値はいくらですか?
解 $ x=2, y=1$ を連立方程式に代入します
$ \begin{eqnarray} \left\{ \begin{array}{l} 2a+b=7 ・・・ ①\\ 2a+2b=4 ・・・ ②\end{array} \right.\end{eqnarray}$
①式から②式を引きます
$ -b=3$
$ b=-3$ ・・・ ③
③式を①式に代入します
$ 2a-3=7$
$ 2a=10$
$ a=5$
$ a=5,b=-3$ (答え)
因数分解
因数分解とは,式を積の形にすることです。分配の法則の逆や、乗法の公式の逆や、たすきがけの法則を使って因数分解をします。
分配の法則の逆を使った因数分解
<例>
$ 2x+4y$ を因数分解すると
$ 2x+4y=2(x+2y)$
$ 4x^2+2x$ を因数分解すると
$ 4x^2+2x=2x(2x+1)$
乗法の公式の逆を使った因数分解
<例>
$ x^2+2xy+y^2$ を因数分解すると
$ x^2+2xy+y^2=(x+y)^2$
$ x^2-y^2$ を因数分解すると
$ x^2-y^2=(x+y)(x-y)$
たすきがけを使った因数分解
<例>
$ acx^2+(ad+bc)x+bd$
を因数分解すると乗法の公式より、
$ acx^2+(ad+bc)x+bd=(ax+b)(cx+d)$
になります。
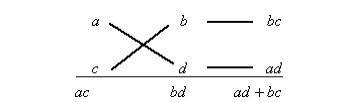
たすきがけの法則とは、
こんなイメージです。
イメージでは分かりにくいので、数値を入れて考えてみます。
例えば、$ 3x^2+10x+8$ の因数分解を行ってみます。
$ 3x^2+10x+8=(ax+b)(cx+d)$
となればいいのですから、
$ ac=3 , bd=8 , ac+bd=10$
となるような、$ a , b , c , d$ を考えます。
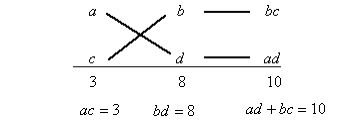
まず、$ ac=3$に着目します。$ ac=3$ となるには、$ a=3,b=1$ または、$ a=1,b=3$ ですので、
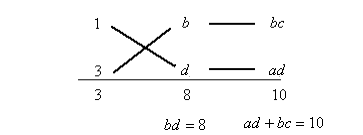
になります。次に$ bd=8$ となるように考えます。$ bd=8$ となる数字は、
$ (b,d)=(1,8)、(8,1)、(2,4)、(4,2)$
の4パターンですので、総あたりで考えます。
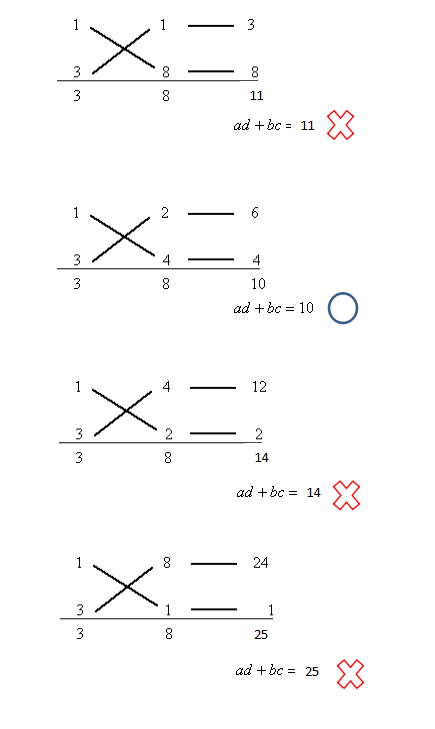
成立するのは
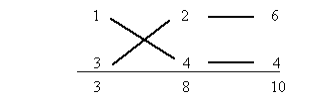
のみですので、$ a=1,b=3,c=2,d=4$ となり、答えは
$ 3x^2+10x+8=(x+2)(3x+4)$
となります。
因数分解は後ほど出てくる、2次方程式を解くのに使います。電験3種の計算問題で、2次方程式の解を求める問題は頻出していますので、使いこなせるように練習をしておいて下さい。
演習問題4
次の式を因数分解できますか?
1. $ x^2-1=$
2. $ 24ax+18bx=$
3. $ ax-5a-x+5=$
4. $ 2x^2+3x+1=$
5. $ 3ax^2-18ax+24a=$
演習問題4の解答
1の解答
$ x^2-1$
$ =(x+1)(x-1)$
2の解答
$ 24ax+18bx$
$ =6x(4a+3b)$
3の解答
$ ax-5a-x+5$
$ =a(x-5)-(x-5)$
$ =(a-1)(x-5)$
4の解答
$ 2x^2+3x+1$
$ =(2x+1)(x+1)$
5の解答
$ 3ax^2-18ax+24a$
$ =3a(x^2-6x+8)$
$ =3a(x-2)(x-4)$
平方根
平方根の意味と計算のルールについて、理解しておきましょう。
平方根とは
平方根とは2乗の逆のことです。2乗するとaになる数を、『aの平方根』といいます。例えば、2×2=4 ですので、2を2乗すると4になります。このような関係にある時に、「2は4の平方根」といいます。
また、(-2)×(-2)=4 ですので、(-2)を2乗すると4になります。(-2)についても、「(-2)は4の平方根」といいます。
つまり、4の平方根は ±2 となります。同じように考えると
9の平方根 ⇒ ±3
16の平方根 ⇒ ±4
25の平方根 ⇒ ±5
と、なることは理解できると思います。
では、3の平方根は?これは、$ \sqrt{}$ を使って表現します。
3の平方根 ⇒ ±$ \sqrt{3}$
逆を言えば、$ \sqrt{3}$ と ー$ \sqrt{3}$ は2乗すると3になる数です。
次のような関係も理解できると思います。
4の平方根
⇒ ±$ \sqrt{4}$ = ±$ \sqrt{2×2}$ = ±2
5の平方根
⇒ ±$ \sqrt{5}$
6の平方根
⇒ ±$ \sqrt{6}$
7の平方根
⇒ ±$ \sqrt{7}$
8の平方根
⇒ ±$ \sqrt{8}$
9の平方根
⇒ ±$ \sqrt{9}$ = ±$ \sqrt{3×3}$ = ±3
ここで、$ \sqrt{8}$ に注目してください。$ \sqrt{8}$ は
±$ \sqrt{8}$ = ±$ \sqrt{2×2×2}$
です。
±$ \sqrt{8}$ = ±$ 2\sqrt{2}$
のように、2の2乗を$ \sqrt{}$ の外へ出すことが出来ます。
平方根計算のルール
平方根の積と商は、そのまま計算できます。
$ \sqrt{3}×\sqrt{7}=\sqrt{3×7}=\sqrt{21}$
$ \displaystyle \frac{\sqrt{6}}{\sqrt{2}}=\sqrt{\frac{6}{2}}=\sqrt{3}$
根号を含む加法・減法は文字式の計算と同じように考えます。
$ 2\sqrt{5}+3\sqrt{5}=5\sqrt{5}$
$ 4+4\sqrt{2}-\sqrt{2}=4+3\sqrt{2}$
$ 2\sqrt{5}+3\sqrt{5}+4\sqrt{2}-\sqrt{2}=5\sqrt{5}+3\sqrt{2}$
根号の中の数はできるだけ簡単にします。
$ \sqrt{50}=\sqrt{2×25}=\sqrt{2×5^2}=5\sqrt{2}$
$ \sqrt{252}=\sqrt{2×2×3×3×7}=\sqrt{2^2×3^2×7}$
$ =2×3×\sqrt{7}=6\sqrt{7}$
分配法則や乗法の公式を用いて計算することができます。
$ \sqrt{2}(\sqrt{6}+3)=\sqrt{2}×\sqrt{6}+\sqrt{2}×3$
$ =\sqrt{12}+3\sqrt{2}=2\sqrt{3}+3\sqrt{2}$
分母には根号をつけません(有理化)
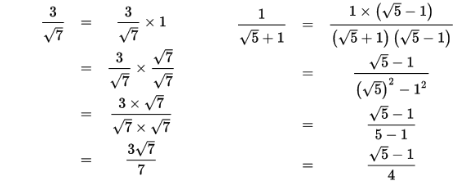
演習問題5
次の計算ができますか?
1. $ \sqrt{63}=$
2. $ \sqrt{12}+\sqrt{27}=$
3. $ (\sqrt{3}×\sqrt{7})^2=$
4. $ (4\sqrt{2}+\sqrt{3})^2=$
5. $ \displaystyle \frac{1}{\sqrt{5}+\sqrt{2}}=$
演習問題5の解答
1の解答
$ \sqrt{63}$
$ =\sqrt{9×7}$
$ =\sqrt{3^2×7}$
$ =\sqrt{3^2}×\sqrt{7}$
$ =3\sqrt{7}$
2の解答
$ \sqrt{12}+\sqrt{27}$
$ =\sqrt{4×3}+\sqrt{9×3}$
$ =\sqrt{2^2×3}+\sqrt{3^2×3}$
$ =\sqrt{2^2}×\sqrt{3}+\sqrt{3^2}×\sqrt{3}$
$ =2\sqrt{3}+3\sqrt{3}$
$ =5\sqrt{3}$
3の解答
$ (\sqrt{3}×\sqrt{7})^2$
$ =(\sqrt{21})^2$
$ =21$
4の解答
$ (4\sqrt{2}+\sqrt{3})^2$
$= (4\sqrt{2})^2+2×4\sqrt{2}×\sqrt{3}+(\sqrt{3})^2$
$= 32+8\sqrt{6}+3$
$= 35+8\sqrt{6}$
5の解答
$ \displaystyle \frac{1}{\sqrt{5}+\sqrt{2}}$
$ =\displaystyle \frac{\sqrt{5}-\sqrt{2}}{(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})}$
$ =\displaystyle \frac{\sqrt{5}-\sqrt{2}}{(\sqrt{5})^2-(\sqrt{2})^2}$
$ =\displaystyle \frac{\sqrt{5}-\sqrt{2}}{3}$
2次方程式
xの2乗の項を含む方程式を2次方程式といいます。2次方程式を解くには、①平方根の利用、②因数分解の利用、③解の公式の利用で解くことができます。
平方根の利用による2次方程式の解きかた
$ x^2=5$
$ x=±\sqrt{5}$
$ x^2-9=0$
$ x^2=9$
$ x=±3$
$ (x-5)^2-16=0$
$ (x-5)^2=16$
$ (x-5)=±4$
$ x=9,1$
因数分解の利用2による次方程式の解きかた
$ x^2-5x=0$
$x(x-5)=0$
$ x=0,5$
$ x^2+6x+9=0$
$ (x+3)^2=0$
$ x=-3$
$ x^2-5x+6=0$
$ (x-2)(x-3)=0$
$ x=2,3$
解の公式の利用による次方程式の解きかた
2次方程式を$ ax^2+bx+c=0$ の形にして、公式に当てはめれば2次方程式を解くことができます。 解の公式は必ず覚えておきましょう。
2次方程式 $ ax^2+bx+c=0 (a\neq 0)$の解の公式は
$ x=\displaystyle \frac{-b\pm \sqrt{b^2-4ac}}{2a} $
となります。
$ x^2+8x+3=0$
$ x=\displaystyle \frac{-8\pm \sqrt{8^2-4×1×3}}{2} $
$ x=\displaystyle \frac{-8\pm \sqrt{64-12}}{2} $
$ x=\displaystyle \frac{-8\pm \sqrt{52}}{2} $
$ x=\displaystyle \frac{-8\pm 2\sqrt{13}}{2} $
$ x=-4\pm \sqrt{13} $
$ x^2+x-2=0$
$ x=\displaystyle \frac{-1\pm \sqrt{1^2-4×1×(-2)}}{2} $
$ x=\displaystyle \frac{-1\pm \sqrt{9}}{2} $
$ x=\displaystyle \frac{-1\pm 3}{2} $
$ x=1,-2 $
演習問題6
次の2次方程式が解けますか?
1. $ 2x^2-32=0$
2. $ 2x^2-6x+3=0$
3. $ 3x^2+6x-45=0$
4. $ x^2+16x+10=3(x-10)$
5. $ \displaystyle (x-\frac{1}{3})^2-\frac{4}{9}=0$
演習問題6の解答
1の解答
$ 2x^2-32=0$
$ 2x^2=32$
$ x^2=16$
$ x=±4$
2の解答
$ 2x^2-6x+3=0$
$ x=\displaystyle \frac{6\pm \sqrt{(-6)^2-4×2×3}}{2×2} $
$ x=\displaystyle \frac{6\pm \sqrt{36-24}}{4} $
$ x=\displaystyle \frac{6\pm \sqrt{12}}{4} $
$ x=\displaystyle \frac{6\pm 2\sqrt{3}}{4} $
$ x=\displaystyle \frac{3\pm \sqrt{3}}{2} $
3の解答
$ 3x^2+6x-45=0$
$ x^2+2x-15=0$
$ (x+5)(x-3)=0$
$ x=-5,3$
4の解答
$ x^2+16x+10=3(x-10)$
$ x^2+16x+10=3x-30$
$ x^2+16x-3x+10+30=0$
$ x^2+13x+40=0$
$ (x+5)(x+8)=0$
$ x=-5,-8$
5の解答
$ \displaystyle (x-\frac{1}{3})^2-\frac{4}{9}=0$
$ \displaystyle (x-\frac{1}{3})^2=\frac{4}{9}$
$ \displaystyle (x-\frac{1}{3})=±\frac{2}{3}$
$ x=\displaystyle\frac{1}{3}±\frac{2}{3}$
$ x=1,-\displaystyle\frac{1}{3}$
以上が電気数学を学ぶ前に必要な中学校で習う数学の計算についてのおさらいです。このページの演習問題で不安を感じた方は、電験3種の問題を解くには非常に厳しいです。もう少し演習問題を行って計算の基礎知識を身に付けることをお勧めします。ちびむすドリルというサイトに計算問題のプリントがたくさんありますので、しっかりと演習をしてください。



