ホイートストンブリッジ回路

このページでは、ホイートストンブリッジ回路と分圧の法則、分流の法則について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題されたホイートストンブリッジ回路と分圧の法則、分流の法則の過去問題の求め方も解説しています。

分圧の法則

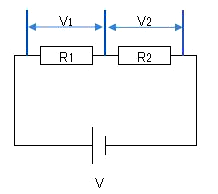
図のような直列回路の電圧は、$V=V_1+V_2$ です。回路の合成抵抗を $R$ とすると、$R=R_1+R_2$ になります。この回路に流れる電流を $I$ とすれば、$I=\displaystyle \frac{V_1 }{ R_1 }=\displaystyle \frac{V_2 }{ R_2 }$ の関係式が成立します。これらをオームの法則に適用すると、

$V=RI=(R_1+R_2)I$

$V=(R_1+R_2)×\displaystyle\frac{V_1 }{ R_1 }=(R_1+R_2)×\displaystyle\frac{V_2 }{ R_2 }$

分流の法則

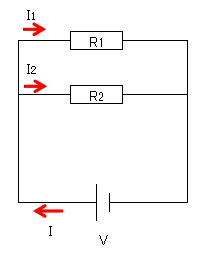
図のような並列回路の電流は、$I=I_1+I_2$ です。回路の合成抵抗を $R$ とすると、$R=\displaystyle \frac{R_1R_2 }{ R_1+R_2 }$ になります。この回路にの電圧を $V$ は、$V= R_1 I_1=R_2 I_2$ の関係式が成立します。これらをオームの法則に適用すると、

$V=RI=\displaystyle \frac{R_1R_2 }{ R_1+R_2 }I=R_1 I_1=R_2 I_2$

上下対象回路

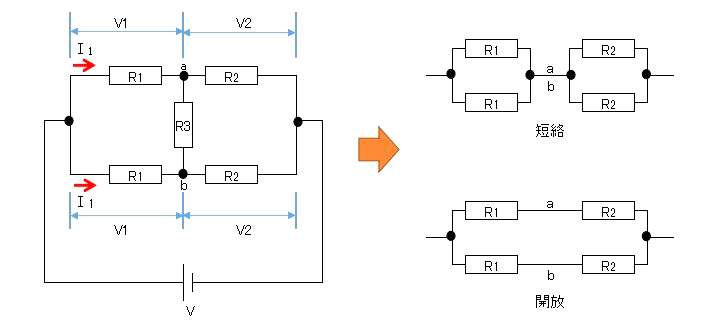
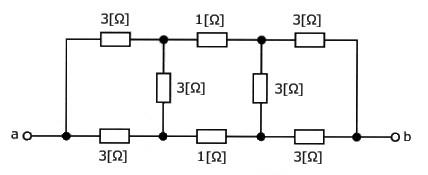
図のように、上下とも同じ抵抗値の回路を対象回路といいます。このような回路では上側に流れる電流と下側に流れる電流は、同じ値になります。電流が同じ値ということは、上下の $R_1$ で電圧降下も同じです。

それは、a端子とb端子に電位差がないということで、ab間には電流が流れません。つまり、「短絡しても開放しても流れる電流は変化しません。」

このように対象回路では、電位の等しい点を、「短絡］または「開放」して回路を簡単にすることができます。

ホイートストンブリッジ回路

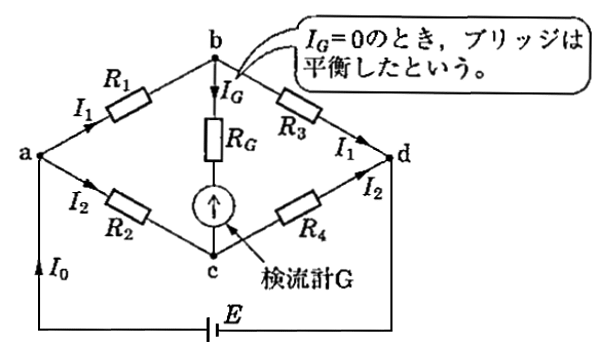
図のような回路をホイートストンブリッジ回路といいます。ブリッジ回路では、$R_1×R_4＝R_2×R_3$ の条件を満たす場合に、平衡したといいます。

ブリッジ回路が平衡しているときは、端子 bc間の電位差は 0［V］になります。つまり検流計 G には電流が流れません。

　　

電験三種－理論（直流回路）過去問題

(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。

1998年（平成10年）問4

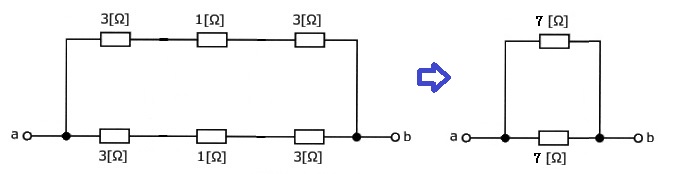
図のような回路において、端子 ab間の合成抵抗［Ω］の値として、正しいのは次のうちどれか。

(1) 2.5　(2) 3.0　(3) 3.5　(4) 4.0　(5) 4.5

1998年（平成10年）問4　過去問解説

回路は上下で対象な回路です。等価回路を開放で考えると、

となります。合成抵抗 $R$［Ω］は、

$R=\displaystyle \frac{7 }{ 2}=3.5$［Ω］

答え (3)

2000年（平成12年）問10

図の直流回路において、電源を流れる電流 $I$［A］の値として、正しいのは次のうちどれか。

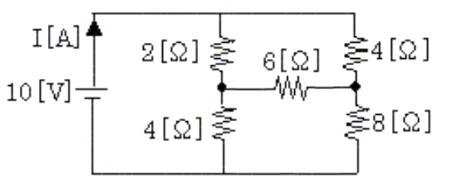
(1) 1.0　(2) 1.5　(3) 2.0　(4) 2.5　(5) 3.0

2000年（平成12年）問10　過去問解説

ブリッジ回路が平衡しています。等価回路を開放で考えると、

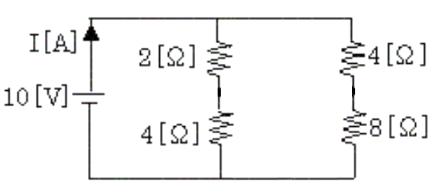
となります。合成抵抗 $R$［Ω］は、

$R=\displaystyle \frac{6×12 }{ 6+12}=4$［Ω］

電流 $I$［A］は

$4I=10$
$I=2.5$

答え (4)

2002年（平成14年）問5

図のような、抵抗 $P=1$［kΩ］、抵抗 $Q=10$［Ω］のホイートストンブリッジ回路がある。このブリッジ回路において、抵抗 $R$ は $100$［Ω］～$2$［kΩ］の範囲内にある。この $R$ のすべての範囲でブリッジの平衡条件を満たす可変抵抗 $S$ の値の範囲として、正しいのは次のうちどれか。

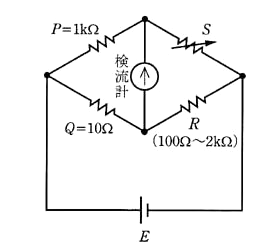
1. 0.5［Ω］～ 10［Ω］
2. 10 ［Ω］～ 200［Ω］
3. 500［Ω］～ 5［kΩ］
4. 10 ［kΩ］～ 200［kΩ］
5. 500［kΩ］～ 1［MΩ］

2002年（平成14年）問5　過去問解説

ホイートストンブリッジ回路の平衡条件は、$PR=QS$ ですので、

$R=100$ のとき

$1000×100＝10×S$
$S=10000=10$［kΩ］

$R=2000$ のとき

$1000×2000＝10×S$
$S=200000=200$［kΩ］

答え (4)

2004年（平成16年）問5

図のような直流回路において、抵抗 3［Ω］の端子間の電圧が 1.8［V］であった。このとき、電源電圧 $E$［V］の値として、正しいのは次のうちどれか。

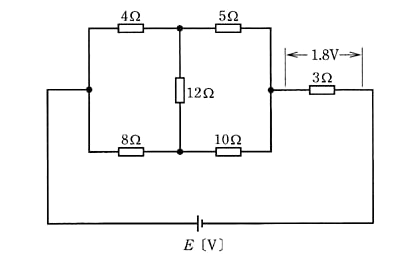
(1) 1.8　(2) 3.6　(3) 5.4　(4) 7.2　(5) 10.4

2004年（平成16年）問5　過去問解説

ブリッジ回路が平衡しています。等価回路を開放で考え、並列回路部分の合成抵抗 $R$は

$R=\displaystyle \frac{9×18 }{ 9+18}=6$［Ω］

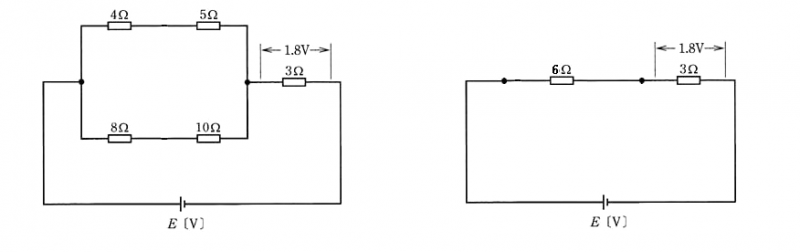
分圧の法則より

$V_1 =\displaystyle\frac{R_1 }{ R_1+R_2 }E$
$1.8 =\displaystyle\frac{3}{ 6+3 }E$
$E =5.4$ ［V］

答え (3)

2005年（平成17年）問5

図のように、抵抗 $R_{ab}=140$［Ω］のすべり抵抗器に抵抗 $R_1=10$［Ω］、抵抗 $R_2=5$［Ω］を接続した回路がある。この回路を流れる電流が $I=9$［A］のとき、抵抗 $R_1$ を流れる電流 $I_1=3$［A］であった。このときのすべり抵抗器の抵抗比（抵抗 $R_{ac}$：抵抗 $R_{bc}$）の値として、正しいのは次のうちどれか。

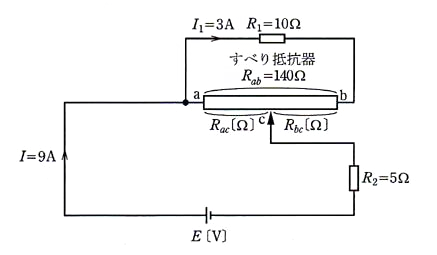
(1) 1：13　(2) 1：3　(3) 5：9　(4) 9：5　(5) 13：1

2005年（平成17年）問5　過去問解説

等価回路図を示します。

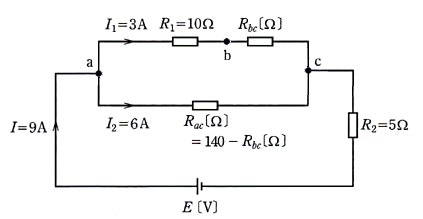
抵抗 $R_{ac}$ に流れる電流を $I_2$［A］とすると、

$I_2=I-I_1=9-3=6$［A］

分流の法則より、$I_1:I_2=R_{ab}:R_1+R_{bc}$ の関係になりますので、

$I_1:I_2=R_{ab}:R_1+R_{bc}$
$3:6=140-R_{bc}:10+R_{bc}$
$10+R_{bc}=2(140-R_{bc})$
$R_{bc}=90$［Ω］
$R_{ac}=140-R_{bc}=50$［Ω］

したがって、$R_{ac}:R_{bc}=50:90=5:9$

答え (3)

2007年（平成19年）問6

図のような直流回路において、スイッチＳを閉じても、開いても電流計の指示値は、$\displaystyle\frac{E}{ 4 }$［A］一定である。このとき、抵抗 $R_3$［Ω］，$R_4$［Ω］のうち小さいほうの抵抗［Ω］の値として、正しいのは次のうちどれか。
ただし、直流電圧源は $E$［V］とし、電流計の内部抵抗は無視できるものとする。

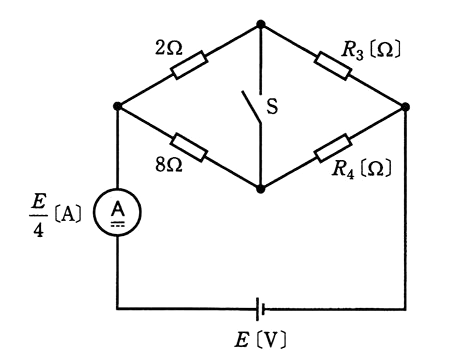
(1) 1　(2) 2　(3) 3　(4) 4　(5) 8

2007年（平成19年）問6　過去問解説

スイッチを閉じても開いても電流計の指示が一定であるということは，ブリッジ回路が平衡していることです。ホイートストンブリッジ回路の平衡条件より

$2R_4=8R_3$
$R_4=4R_3$

回路の合成抵抗 $R$［Ω］は、

$\begin{eqnarray} R &=& \displaystyle \frac{(8+R_4)(2+R_3) }{ (8+R_4)+(2+R_3)}\\\\&=&\displaystyle \frac{(8+4R_3)(2+R_3) }{ (8+4R_3)+(2+R_3)}\\\\&=&\displaystyle \frac{4(2+R_3)(2+R_3) }{ 10+5R_3}\\\\&=&\displaystyle \frac{4(2+R_3)^2 }{ 5(2+R_3)}\\\\&=&\displaystyle \frac{4 }{ 5}(2+R_3)\end{eqnarray} $

オームの法則より

$E=\displaystyle \frac{4 }{ 5}(2+R_3)×\displaystyle\frac{E}{ 4 } $
$R_3＝3 $
$R_4＝12 $

答え (3)

2010年（平成22年）問6

図１の直流回路において、端子 a-c間に 100［V］を加えたところ、端子 b-c間の電圧は 20［V］であった。また、図２のように端子 b-c間に抵抗 150［Ω］の抵抗を並列に追加したとき、端子 b-c間の端子電圧は 15［V］であった。いま､図３のように端子 b-c間を短絡したとき、電流 $I$［A］の値として正しいのは次のうちどれか。

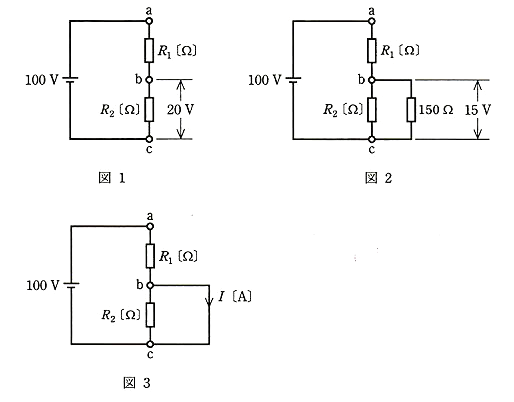
(1) 0　(2) 0.10　(3) 0.32　 (4) 0.40　 (5) 0.67

2010年（平成22年）問6　過去問解説

図１の端子a-b間の電圧は 80［V］なので、抵抗 $R_1$ と $R_2$の比は、

$R_1:R_2=80:20=4:1$
$R_1=4R_2$ … (1)

図２の端子a-b間の電圧は 85［V］なので、抵抗 $R_1$ と 端子 b-c間の合成抵抗の比は、

$R_1:\displaystyle \frac{150 R_2}{ R_2+150}=85:15=17:3$
$3R_1=17×\displaystyle \frac{150 R_2}{ R_2+150}$
$R_1=\displaystyle \frac{850 R_2}{ R_2+150}$ … (2)

(1)、(2)の方程式を解くと

$4R_2(R_2+150)=850 R_2$
$4R_2+600=850$
$4R_2=250=R_1$

端子 b-c間を短絡したとき、電流 $I$［A］は

$I×250=100$
$I=0.4$［A］

答え (4)

2011年（平成23年）問6

図の直流回路において、200［V］の直流電源から流れ出る電流が 25［A］である。16［Ω］と $r$［Ω］の抵抗の接続点 a の電位を $V_a$［V］、8［Ω］と $R$［Ω］の抵抗の接続点 b の電位を $V_b$［V］とする。$V_a=V_b$ となる $r$［Ω］と $R$［Ω］の値の組み合わせとして、正しいものを次の(1)～(5)のうちから一つ選べ。

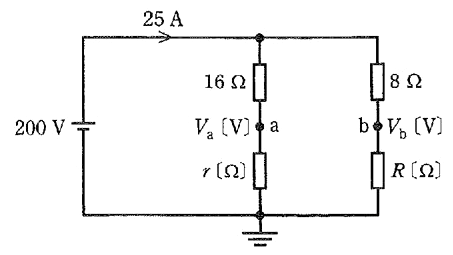
2011年（平成23年）問6　過去問解説

接続点aの電位と接続点bの電位が同じなので、ブリッジ回路の平衡条件を用いることができます。

$16R=8r$
$r=2R$

電源から見た回路の合成抵抗を $R_Z$［Ω］とすると、

$\begin{eqnarray}R_Z&=&\displaystyle \frac{(16+r)(8+R)}{ (16+r)+(8+R)}\\\\&=&\displaystyle \frac{(16+2R)(8+R)}{ (16+2R)+(8+R)}\\\\&=&\displaystyle \frac{2(8+R)^2}{ 3(8+R)}\\\\&=&\displaystyle \frac{2}{ 3}(8+R)［Ω］\end{eqnarray}$

回路に流れる電流と電源電圧の関係より、$R_Z=\displaystyle \frac{200}{ 25}=8$［Ω］なので、

$\displaystyle \frac{2}{ 3}(8+R)=8$

したがって、$R=4,r=8$［Ω］

答え (4)

2011年（平成23年）問7

図のように、可変抵抗 $R_1$［Ω］，$R_2$［Ω］，抵抗 $R_X$［Ω］，電源 $E$［V］からなる直流回路がある。次に示す条件１のときの $R_X$［Ω］に流れる電流 $I$［A］の値と条件２のときの電流 $I$［A］の値は等しくなった。このとき、$R_X$［Ω］の値として、正しいものを次の(1)～(5)のうちから一つ選べ。

条件１：$R_1=90$［Ω］、$R_2=6$［Ω］
条件２：$R_1=70$［Ω］、$R_2=4$［Ω］

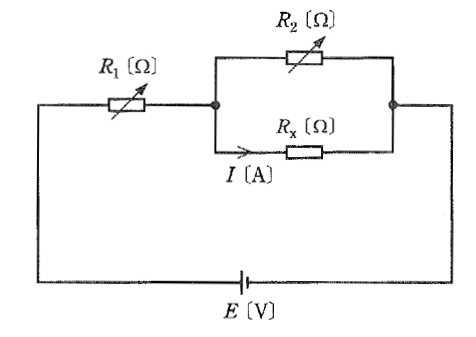
(1) 1　(2) 2　(3) 4　(4) 8　(5) 12

2011年（平成23年）問7　過去問解説

この回路の合成抵抗を $R$ とすると

$R=R_1+\displaystyle \frac{ R_2R_X }{ R_X+R_2 }$

条件 1 のときの合成抵抗 $R$ は、

$R=90+\displaystyle \frac{ 6R_X }{ R_X+6 }$

回路に流れる電流を $ I_1$ とすると、オームの法則より

$ I_1=\displaystyle \frac{E}{90+\displaystyle \frac{ 6R_X }{ R_X+6 }}$

分流の法則より

$ \begin{eqnarray} I&=&I_1×\displaystyle \frac{ R_2 }{ R_X+R_2}\\\\&=&\displaystyle \frac{E}{90+\displaystyle \frac{ 6R_X }{ R_X+6 }}×\frac{ 6 }{ R_X+6}\\\\&=&\displaystyle \frac{ 6E }{96R_X+540 } … (1)\end{eqnarray}$

条件 2 のときの合成抵抗 $R$ は、

$R=70+\displaystyle \frac{ 4R_X }{ R_X+4 }$

回路に流れる電流を $ I_2$ とすると、オームの法則より

$ I_2=\displaystyle \frac{E}{70+\displaystyle \frac{ 4R_X }{ R_X+4}}$

分流の法則より

$ \begin{eqnarray} I&=&I_1×\displaystyle \frac{ R_2 }{ R_X+R_2}\\\\&=&\displaystyle \frac{E}{70+\displaystyle \frac{ 4R_X }{ R_X+4 }}×\frac{ 4}{ R_X+4}\\\\&=&\displaystyle \frac{ 4E }{74R_X+280 } … (2)\end{eqnarray}$

題意より、(1)式＝(2)式なので、

$\displaystyle \frac{ 6E }{96R_X+540 } =\displaystyle \frac{ 4E }{74R_X+280 } $

$4(96R_X+540)=6(96R_X+540)$

$R_X=8$［Ω］

答え (4)

2015年（平成27年）問6

図のように、抵抗とスイッチSを接続した直流回路がある。いま、スイッチSを開閉しても回路を流れる電流 $I$［A］は、$I＝30A$ で一定であった。このとき、抵抗 $R_4$ の値［Ω］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

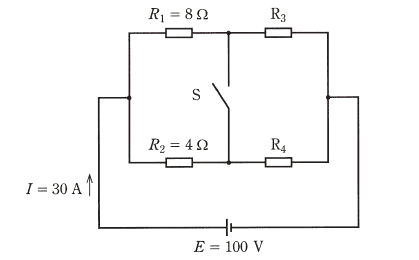
(1) 0.5　(2) 1.0　(3) 1.5　(4) 2.0　(5) 2.5

2015年（平成27年）問6　過去問解説

スイッチSを開閉しても回路を流れる電流が一定であるということは，ブリッジ回路が平衡していることです。ホイートストンブリッジ回路の平衡条件より

$8R_4=4R_3$
$R_3=2R_4$

回路の合成抵抗 $R$［Ω］は、

$\begin{eqnarray} R &=& \displaystyle \frac{(8+R_3)(4+R_4) }{ (8+R_3)+(4+R_4)}\\\\&=&\displaystyle \frac{(8+2R_4)(4+R_4) }{ (8+2R_4)+(4+R_4)}\\\\&=&\displaystyle \frac{2(4+R_4)(4+R_4) }{ 12+3R_4}\\\\&=&\displaystyle \frac{2(4+R_4)^2 }{ 3(4+R_4)}\\\\&=&\displaystyle \frac{2}{ 3}(4+R_4)\end{eqnarray} $

オームの法則より

$100=\displaystyle \frac{2}{ 3}(4+R_4)×30 $
$R_4＝1 $

答え (2)

2016年（平成28年）問6

図のような抵抗の直並列回路に直流電圧 $E＝5V$ を加えたとき、電流比 $\displaystyle \frac{I_2 }{ I_1}$ の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

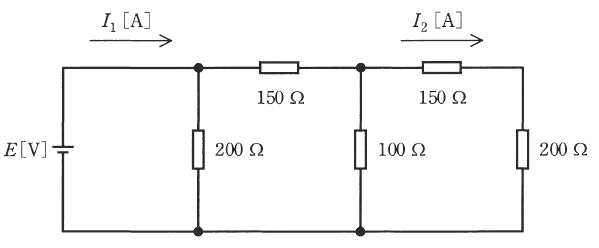
(1) 0.1　(2) 0.2　(3) 0.3　(4) 0.4　(5) 0.5

2016年（平成28年）問6　過去問解説

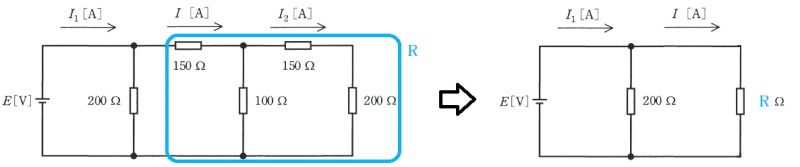
図のように 150［Ω］の抵抗に流れる電流を $I$［A］とすれば、分流の法則より

$I_2=\displaystyle \frac{100 }{ 100+(150+200) }I=\displaystyle \frac{2 }{ 9 }I$［A］ … (1）

図に示す部分の合成抵抗 $R$［Ω］は、

$\begin{eqnarray}R&=&150+\displaystyle \frac{100×(150+200) }{ 100+(150+200) }\\\\&=&150+\displaystyle \frac{700 }{ 9 }\\\\&=&\displaystyle \frac{2050 }{ 9 }［Ω］\end{eqnarray}$

$I$［A］と $I_1$［A］で、分流の法則を適用すると、

$\begin{eqnarray}I&=&\displaystyle \frac{200 }{ 200+R }I_1\\\\&=&\displaystyle \frac{200 }{ 200+\displaystyle \frac{2050 }{ 9 } }I_1\\\\&=&\displaystyle \frac{180 }{ 385 }I_1［A］… (2）\end{eqnarray}$

(1),(2)式より、

$\displaystyle \frac{9 }{ 2 }I_2=\displaystyle \frac{180 }{ 385 }I_1$
$\displaystyle \frac{I_2 }{ I_1}≒0.1$

答え (1)