このページでは、RLC直列共振回路について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の理論科目で、実際に出題されたRLC直列共振回路の過去問題の求め方も解説しています。
$RLC$ 直列回路の共振
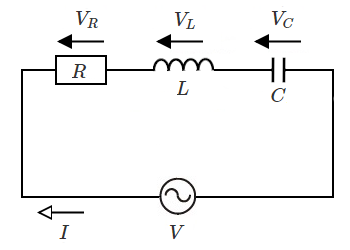
図のように抵抗 $R$、コイル $L$ 、コンデンサ $C$ を直列接続したときの合成インピーダンス $\dot{Z}$ とその大きさ $Z$ は、次のように表すことができます。
$Z=R+jωL+\displaystyle \frac{ 1 }{ jωC }=R+j\left(ωL-\displaystyle \frac{ 1 }{ ωC }\right)$
$Z=\displaystyle\sqrt{R^2+\left(ωL-\displaystyle \frac{ 1 }{ ωC }\right)^2}$
各周波数が、
$ω_0=\displaystyle \frac{ 1 }{ \sqrt{LC} }$
の条件を満たすとき、
$ω_0L=\displaystyle \frac{ 1 }{ ω_0C }$
となります。このとき、インピーダンスの大きさ $Z$ は、最小値 $Z_{min}$ になります。
$Z_{min}=R$
回路に流れる電流の大きさ $I$ は、
$I=\displaystyle\frac{V}{\sqrt{R^2+\left(ωL-\displaystyle \frac{ 1 }{ ωC }\right)^2}}$
で、表すことができますので、各周波数 $ω_0$ のとき、回路に流れる電流は最大値 $I_{max}$ になります。
$I_{max}=\displaystyle\frac{V}{Z_{min}}=\displaystyle\frac{V}{R}$
このように、直列回路で電流が最大値になる現象を共振といいます。また、共振が起こる角周波数 $ω_0$ を共振角周波数といいます。共振が起きたときの、フェーザ図を次に示します。
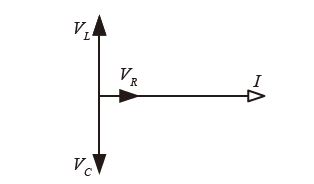
共振が起きたときの各素子の端子間電圧の大きさは、
$V_R=V$
$V_L=\displaystyle\frac{ω_0L}{R}V$
$V_C=\displaystyle\frac{1}{ω_0CR}V$
になります。$V_L$ と $V_C$ は、大きさが等しくまた、逆相となりますので、互いに打ち消しあいます。したがって、電源電圧 $V$ と抵抗両端の電圧 $V_R$ は同じになります。また、電源電圧 $V$ と抵抗両端の電圧 $V_R$ 、電流 $I$ は同相になります。
電験三種－理論（交流回路）過去問題
1997年（平成9年）問8
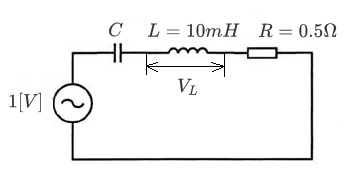
図のような交流回路において、電源の周波数を変化させたところ、共振時のインダクタンス $L$ の端子電圧 $V_L$ が $314V$ であった。共振周波数（kHz）の値として、正しいのはどれか。
(1) 2.0 (2) 2.5 (3) 3.0 (4) 3.5 (5) 4.0
1997年（平成9年）問8 過去問解説
共振が起きたときのインダクタンス $L$ の端子電圧 $V_L$ は、
$V_L=\displaystyle\frac{ω_0L}{R}V=\displaystyle\frac{2πf_0L}{R}V$
$314=\displaystyle\frac{2×3.14×f_0×10×10^{-3}}{0.5}×1$
$f_0=\displaystyle\frac{0.5×314}{2×3.14×10×10^{-3}}=2.5$［kHz］
答え (2)
2004年（平成16年）問6
図のように、$R$［Ω］の抵抗、インダクタンス $L$［H］のコイル、静電容量 $C$［F］のコンデンサを直列に接続した交流回路がある。この回路において、電源 $E$ は周波数を変化できるものとする。電源周波数を変化させたところ、2種類の異なる周波数 $f_1$［Hz］と $f_2$［Hz］に対して、この回路の電源からみたインピーダンス［Ω］の大きさは変わらなかった。このときの $f_1×f_2$ の値として、正しいのは次のうちどれか。
2004年（平成16年）問6 過去問解説
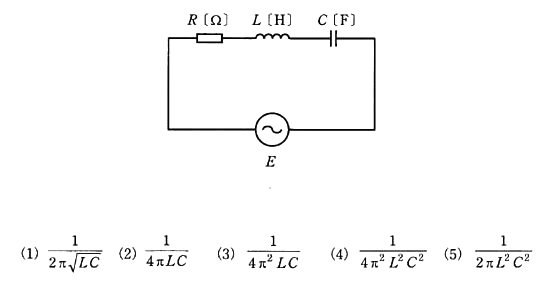
周波数 $f_1$［Hz］のときの合成インピーダンスを $\dot{Z_1}$、 $f_2$［Hz］のときの合成インピーダンスを $\dot{Z_2}$ とすると、周波数の大きさにより、合成インピーダンス $Z_1$，$Z_2$ 一方が誘導性の負荷になると、他方は容量性の負荷になります。周波数 $f_1$［Hz］のときを誘導性負荷、周波数 $f_2$［Hz］のときを容量性負荷と考えると、
$Z_1=\displaystyle\sqrt{R^2+\left(ω_1L-\displaystyle \frac{ 1 }{ ω_1C }\right)^2}$
$Z_2=\displaystyle\sqrt{R^2+\left(\displaystyle \frac{ 1 }{ ω_2C }-ω_2L\right)^2}$
題意より、$Z_1=Z_2$ なので、
$\displaystyle\sqrt{R^2+\left(ω_1L-\displaystyle \frac{ 1 }{ ω_1C }\right)^2}=\displaystyle\sqrt{R^2+\left(\displaystyle \frac{ 1 }{ ω_2C }-ω_2L\right)^2}$
$\left(ω_1L-\displaystyle \frac{ 1 }{ ω_1C }\right)^2=\left(\displaystyle \frac{ 1 }{ ω_2C }-ω_2L\right)^2$
$L(ω_1+ω_2)=\displaystyle \frac{ 1 }{ C }\left(\displaystyle \frac{ 1 }{ ω_1 }+\displaystyle \frac{ 1 }{ ω_2 }\right)$
$L(ω_1+ω_2)=\displaystyle \frac{ 1 }{ C }\left(\displaystyle \frac{ ω_1 + ω_2 }{ ω_1 ω_2 }\right)$
$ω_1 ω_2=\displaystyle \frac{ 1 }{ LC }$
したがって $f_1×f_2$ の値は、
$f_1 f_2=\displaystyle \frac{ 1 }{ 4π^2LC }$
答え (3)
2005年（平成17年）問8
図のように、静電容量 $C_X$［F］及び $C$［F］のコンデンサとインダクタンス $L$［H］のコイルを直列に接続した交流回路がある。この回路において、スイッチSを開いたときの共振周波数は $f_1$［Hz］、閉じたときの共振周波数は $f_2$［Hz］である。$f_1$［Hz］が $f_2$［Hz］の2倍であるとき、静電容量の比 $\displaystyle \frac{C}{C_X}$ の値として、正しいのは次のうちどれか。
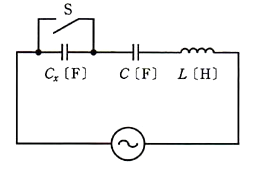
(1) $\displaystyle \frac{1}{3}$ (2) $\displaystyle \frac{1}{2}$ (3) 1 (4) 2 (5) 3
2005年（平成17年）問8 過去問解説
スイッチSを開いたときの合成静電容量を $C_1$［F］、閉じたときの合成静電容量を $C_2$［F］とすると、
$C_1=\displaystyle \frac{C_XC}{C_X+C}$
$C_2=C$
したがって共振周波数 $f_1$［Hz］、 $f_2$［Hz］は、
$f_1=\displaystyle \frac{1}{2π\sqrt{L×\displaystyle \frac{C_XC}{C_X+C}}}$
$f_2=\displaystyle \frac{1}{2π\sqrt{LC}}$
題意より、$f_1=2f_2$［Hz］なので、
$\displaystyle \frac{1}{2π\sqrt{L×\displaystyle \frac{C_XC}{C_X+C}}}=\displaystyle \frac{2}{2π\sqrt{LC}}$
$2\sqrt{L×\displaystyle \frac{C_XC}{C_X+C}}=\sqrt{LC}$
$\displaystyle \frac{4C_XC}{C_X+C}=C$
$3C_X=C$
$\displaystyle \frac{C}{C_X}=3$
答え (5)
2006年（平成18年）問7
図のように、$R=200$［Ω］の抵抗、インダクタンス $L=2$［mH］のコイル、静電容量 $C=0.8$［μF］のコンデンサを直列に接続した交流回路がある。この回路において、電源電圧 $\dot{E}$［V］と電流 $\dot{I}$［A］とが同相であるとき、この電源電圧の角周波数 $ω$［rad/s］の値として、正しいのは次のうちどれか。
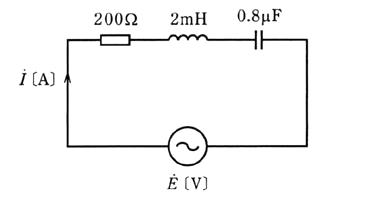
(1) $1.0×10^3$ (2) $3.0×10^3$ (3) $2.0×10^4$ (4) $2.5×10^4$ (5) $3.5×10^4$
2006年（平成18年）問7 過去問解説
電源電圧 $\dot{E}$［V］と電流 $\dot{I}$［A］とが同相ということは、コイル $L$ と、コンデンサ $C$ が直列共振しています。共振角周波数を $ω_0$ とすると、
$ω_0L=\displaystyle \frac{ 1 }{ ω_0C }$
${ω_0}^2=\displaystyle \frac{ 1 }{ LC }$
$=\displaystyle \frac{ 1 }{ 2×10^{-3}×0.8×10^{-6} }$
$=\displaystyle \frac{ 1 }{ 16×10^{-10} }$
$ω_0=\displaystyle \frac{ 1 }{ \sqrt{16×10^{-10} }}=2.5×10^4$［rad/s］
答え (4)
2011年（平成23年）問16
図のように，電圧 $100$［V］に充電された静電容量 $C＝300$［μF］のコンデンサ、インダクタンス $L=30$［mH］のコイル、開いた状態のスイッチＳからなる回路がある。時刻 $t=0$［s］でスイッチＳを閉じてコンデンサに充電された電荷を放電すると、回路には振動電流 $i$［A］（図の矢印の向きを正とする）が流れる。このとき、次の(a)及び(b)の問に答えよ。
ただし、回路の抵抗は無視できるものとする。
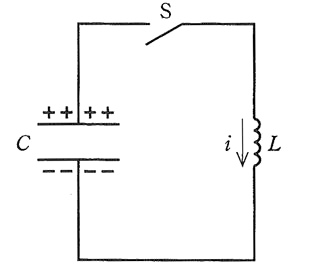
(a) 振動電流 $i$［A］を示す図として、正しいものを次の(1)～(5)のうちから一つ選べ。
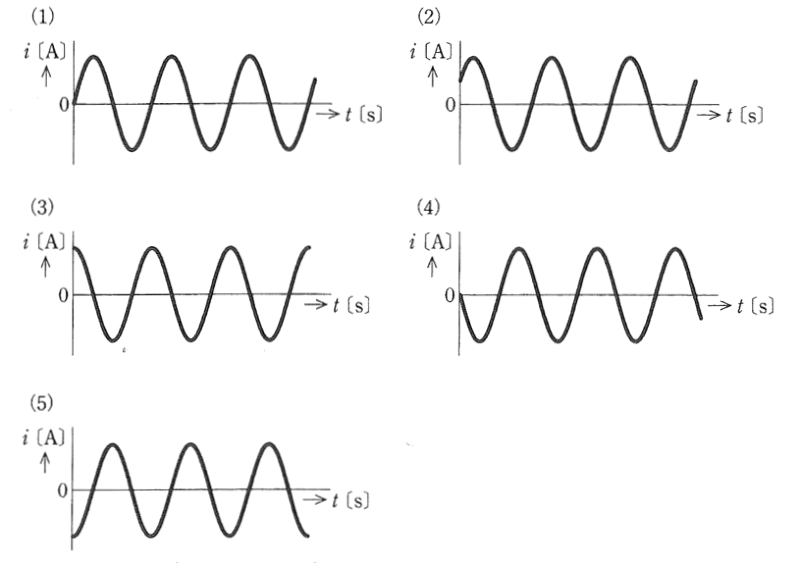
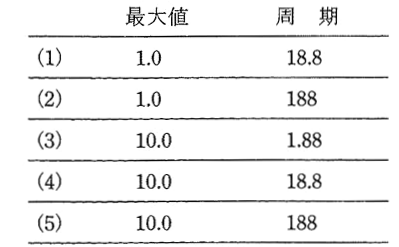
(b) 振動電流の最大値［A］及び周期［ms］の値の組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。
2011年（平成23年）問16 過去問解説
(a) スイッチSを閉じた瞬間はコイルに電流は流れません。つまり、振動電流の初期値は 0［A］です。
$i$ は矢印の向きの正方向（＋方向）に流れはじめます。
したがって、(1)の図が正解になります。
答え (1)
(b) コンデンサに蓄えられたエネルギーを $W_C$［J］、コイルに蓄えられたエネルギーを $W_L$［J］とすると、 $W_C=W_L$ の関係になるので、
$\begin{eqnarray}W_C&=&\displaystyle \frac{1}{2}CV^2\\\\&=&\displaystyle \frac{1}{2}×300×10^{-6}×100^2\\\\&=&1.5\end{eqnarray}［J］$
$\begin{eqnarray}W_L&=&\displaystyle \frac{1}{2}LI^2\\\\&=&\displaystyle \frac{1}{2}×30×10^{-3}×I^2\\\\&=&15×10^{-3}×I^2\end{eqnarray}［J］$
$15×10^{-3}×I^2=1.5$
$I=10.0$［A］
共振周波数を $f_0$［Hz］とすると、
$f_0=\displaystyle \frac{1}{2π\sqrt{LC}}$
$f_0=\displaystyle \frac{1}{2π\sqrt{0×10^{-3}×300×10^{-6}}}≒53.05$［Hz］
周期 $T$［s］は、
$T=\displaystyle \frac{1}{f_0}=\displaystyle \frac{1}{53.05}≒18.8$［ms］
答え (4)
2012年（平成24年）問7
$R$ [Ω] の抵抗、インダクタンス $L$ [H] のコイル、静電容量 $C$ [F] のコンデンサを直列に接続した回路がある。
この回路に交流電圧を加え、その周波数を変化させると、特定の周波数 $f_r$ [Hz] のときに誘導性リアクタンス $=2πf_rL$［Ω］と容量性リアクタンス $＝\displaystyle\frac{1}{ 2πf_rC }$ の大きさが等しくなり、その作用が互いに打ち消し合って回路のインピーダンスが（ ア ）なり、（ イ ）電流が流れるようになる。この現象を直列共振といい、このときの周波数 $f_r$ [Hz] をその回路の共振周波数という。
回路のリアクタンスは共振周波数 $f_r$ [Hz] より低い周波数では（ ウ ）となり、電圧より位相が（ エ ）電流が流れる。また、共振周波数 $f_r$ [Hz] より高い周波数では（ オ ）となり、電圧より位相が（ カ ）電流が流れる。
上記の記述中の空白箇所(ア)、(イ)、(ウ)、(エ)、(オ)及び(カ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。
2012年（平成24年）問7 過去問解説
$R$ [Ω] の抵抗、インダクタンス $L$ [H] のコイル、静電容量 $C$ [F] のコンデンサを直列に接続した回路がある。
この回路に交流電圧を加え、その周波数を変化させると、特定の周波数 $f_r$ [Hz] のときに誘導性リアクタンス $=2πf_rL$［Ω］と容量性リアクタンス $＝\displaystyle\frac{1}{ 2πf_rC }$ の大きさが等しくなり、その作用が互いに打ち消し合って回路のインピーダンスが（ 小さく ）なり、（ 大きな ）電流が流れるようになる。この現象を直列共振といい、このときの周波数 $f_r$ [Hz] をその回路の共振周波数という。
回路のリアクタンスは共振周波数 $f_r$ [Hz] より低い周波数では（ 容量性 ）となり、電圧より位相が（ 進んだ ）電流が流れる。また、共振周波数 $f_r$ [Hz] より高い周波数では（ 誘導性 ）となり、電圧より位相が（ 遅れた ）電流が流れる。
答え (3)
2013年（平成25年）問10
図は、インダクタンス $L$［H］のコイルと静電容量 $C$［F］のコンデンサ並びに $R$［Ω］の抵抗の直列回路に、周波数が $f$［Hｚ］で実効値が $V$（≠０）［V］である電源電圧を与えた回路を示している。この回路において、抵抗の端子間電圧の実効値 $V_R$［V］が零となる周波数 $f$［Hz］の条件を全て列挙したものとして、正しいものを次の(1)～(5)のうちから一つ選べ。
2013年（平成25年）問10 過去問解説
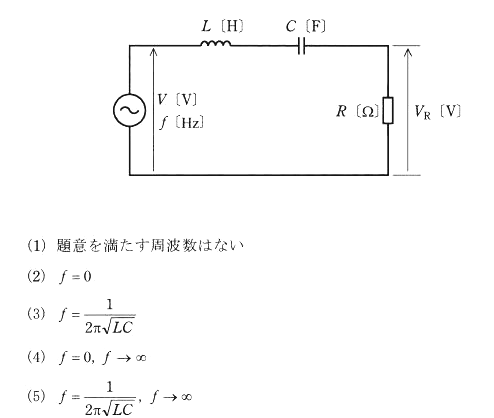
抵抗の端子間電圧の実効値 $V_R=0$［V］ということは、回路に流れる電流は最大値 $I_{max}$ になります。つまり、直列共振が起きています。
誘導性リアクタンスを $X_L$、コイルに流れる電流を $I_L$、コイル両端の電圧を $V_L$ とすると、
$I_L=\displaystyle \frac{ V_L }{ X_L }=\displaystyle \frac{ V_L }{ 2πfL }$
$I_L=0$ になるためには、$f=∞$ になります。
容量性リアクタンスを $X_C$、コンデンサに流れる電流を $I_C$、コイル両端の電圧を $V_C$ とすると、
$I_C=\displaystyle \frac{ V_C }{ X_C }=2πfCV_C$
$I_C=0$ になるためには、$f=0$ になります。
答え (4)
2014年（平成26年）問9
図のように、二つのLC直列共振回路A、Bがあり、それぞれの共振周波数が $f_A$［Hz］、$f_B$［Hz］である。これらA、Bをさらに直列に接続した場合、全体としての共振周波数が $f_{AB}$［Hz］になった。$f_A$、$f_B$、$f_{AB}$ の大小関係として、正しいものを次の(1)～(5)のうちから一つ選べ。
2014年（平成26年）問9 過去問解説
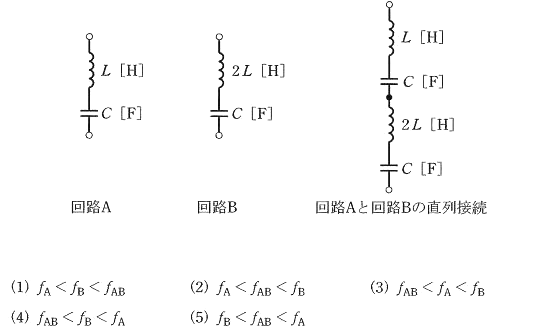
共振周波数は、$f_0＝\displaystyle \frac{ 1}{ 2π\sqrt{LC} }$ なので、回路Ａ，回路Ｂ，回路Ｃ の共振周波数は、
$f_A=\displaystyle \frac{ 1}{ 2π\sqrt{LC} }$
$f_B=\displaystyle \frac{ 1}{ 2π\sqrt{2LC} }=\displaystyle \frac{ 1}{ 2π\sqrt{LC} }×\displaystyle \frac{1}{\sqrt{2}} $
$f_{AB}=\displaystyle \frac{ 1}{ 2π\sqrt{3L×\frac{C}{2}} }=\displaystyle \frac{ 1}{ 2π\sqrt{LC} }×\displaystyle \frac{1}{\sqrt{1.5}} $
したがって、$f_B<f_{AB}<f_{A}$ になります。
答え (5)
