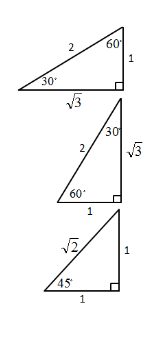三角比と三角関数は、高校2年生までに習う範囲です。電験3種の電気の問題を解く際に特に重要な数学の知識となります。ここはしっかりと勉強をしておいてください。
三角比
三角比とは直角三角形に3つある辺のうち、2つの辺の比を表しています。
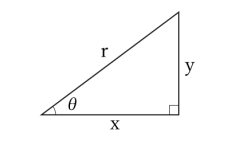
図のような直角三角形で、一番長い辺cを斜辺、水平の辺aを底辺、垂直の辺bを高さと呼びます。
この辺の内から2つを選んで比をとると、
$ \displaystyle \frac{ 高さ }{ 斜辺 },\displaystyle \frac{ 底辺 }{ 斜辺 },\displaystyle \frac{ 高さ}{ 底辺},\displaystyle \frac{ 斜辺}{ 底辺},\displaystyle \frac{ 斜辺}{ 高さ},\displaystyle \frac{ 底辺}{ 高さ}$
の6つの比を作ることができます。この6つの比を三角比というのですが、特にある角度$ θ$(シータ)において、
$ \displaystyle \frac{ 高さ }{ 斜辺 }=\displaystyle \frac{ y }{ r },\displaystyle \frac{ 底辺 }{ 斜辺 }=\displaystyle \frac{ x}{ r },\displaystyle \frac{ 高さ}{ 底辺}=\displaystyle \frac{ y }{ x }$
は、他と区別するために次のように表記されます。
$ sinθ=\displaystyle \frac{ 高さ }{ 斜辺 }=\displaystyle \frac{ y }{ r }$
$ cosθ=\displaystyle \frac{ 底辺 }{ 斜辺 }=\displaystyle \frac{ x}{ r }$
$ tanθ=\displaystyle \frac{ 高さ}{ 底辺}=\displaystyle \frac{ y }{ x }$
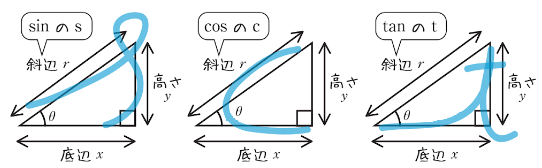
三角比の覚え方としまして、$ sin,cos,tan$ の頭文字をとって、筆記体の書き順で何が分母で何が分子にくるかが分かるといった覚え方が有名です。
つぎの図は三平方の定理で勉強した、特別な三角比です。これを$ sin,cos,tan$ を使って三角比を表わせば、
$ sin30^{ \circ }=\displaystyle\frac{ 1}{ 2} , cos30^{ \circ }=\displaystyle\frac{ \sqrt{ 3 }}{ 2} , tan30^{ \circ }=\displaystyle\frac{ 1}{ \sqrt{ 3 }}$
$ sin60^{ \circ }=\displaystyle\frac{ \sqrt{ 3 }}{ 2} , cos60^{ \circ }=\displaystyle\frac{ 1}{ 2} , tan60^{ \circ }=\sqrt{ 3 }$
$ sin45^{ \circ }=\displaystyle\frac{ 1}{ \sqrt{ 2 }} , cos45^{ \circ }=\displaystyle\frac{ 1}{ \sqrt{ 2 }} , tan45^{ \circ }=1$
となります。
三角関数
三角関数とは、単位円を定義として三角比を扱う関数です。つまり、円を利用して三角比の値を変換するルールのことです。尚、三角関数は円関数ともいいます。
単位円を使った三角比の考え方
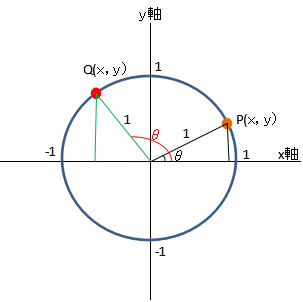
単位円とは半径1の円のことです。右の図のようにx軸とy軸上に単位円を書き、円上の点をP,Qとします。Pの座標(x,y)のxは直角三角形の底辺で、yは直角三角形の高さです。これを三角比で表すと、
$ sinθ=\displaystyle\frac{ y }{ 1 }$ ⇒ $ y=sinθ$
$ cosθ=\displaystyle\frac{ x }{ 1 }$ ⇒ $ x=cosθ$
となります。
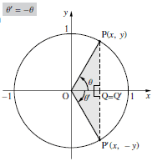
同様にQで考えてみます。Qの座標(x,y)のxは直角三角形の底辺で、yは直角三角形の高さですので、これを三角比で表すと、
$ sinθ=\displaystyle\frac{ y }{ 1 }$ ⇒ $ y=sinθ$
$ cosθ=\displaystyle\frac{ -x }{ 1 }$ ⇒ $ x=-cosθ$
となります。
この考え方を利用すれば、$ 90°<θ<360°$ の範囲においても、三角比を使うことが出来るようになります。この考え方が「三角関数」といえます。
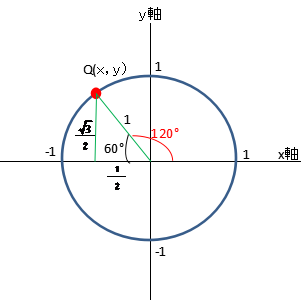
例として、$ θ=120°$ の$ sinθ,cosθ,tanθ$ を求めてみます。
図のように60°の直角三角形として考えることができますので、60°の直角三角形の比は
斜辺:高さ:底辺=2:1:$ \sqrt{ 3 }$
ですので、底辺の長さは$ \frac{ 1 }{ 2 }$、高さは$ \frac{ \sqrt{ 3 }}{ 2}$となります。
Qを座標(x,y)で考えると、$ x=-\frac{ 1 }{ 2 }$、$ y=\frac{ \sqrt{ 3 }}{ 2}$ となり、
$ sin120^{ \circ }=\displaystyle\frac{ \sqrt{ 3 }}{ 2}$
$ cos120^{ \circ }=-\displaystyle\frac{1}{ 2}$
$ tan120^{ \circ }=-\sqrt{ 3 }$
となります。
このように、単位円をイメージすると$ 0°<θ<360°$ の任意の範囲において、三角比を求めやすくなります。
参考に$ 0°≦θ≦360°$ の三角関数の表を示します。
| θ | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
| sinθ | 0 | $ \frac{1}{ 2}$ | $ \frac{ 1}{ \sqrt{ 2 }}$ | $ \frac{ \sqrt{ 3 }}{ 2}$ | 1 | $ \frac{ \sqrt{ 3 }}{ 2}$ | $ \frac{ 1}{ \sqrt{ 2 }}$ | $ \frac{1}{ 2}$ | 0 |
| cosθ | 1 | $ \frac{ \sqrt{ 3 }}{ 2}$ | $ \frac{ 1}{ \sqrt{ 2 }}$ | $ \frac{1}{ 2}$ | 0 | $ -\frac{1}{ 2}$ | $ -\frac{ 1}{ \sqrt{ 2 }}$ | $ -\frac{ \sqrt{ 3 }}{ 2}$ | -1 |
| tanθ | 0 | $ \frac{ 1}{ \sqrt{ 3 }}$ | 1 | $ \sqrt{ 3 }$ | なし | $ -\sqrt{ 3 }$ | -1 | $ -\frac{ 1}{ \sqrt{ 3 }}$ | 0 |
| θ | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sinθ | $ -\frac{1}{ 2}$ | $ -\frac{ 1}{ \sqrt{ 2 }}$ | $ -\frac{ \sqrt{ 3 }}{ 2}$ | -1 | $ -\frac{ \sqrt{ 3 }}{ 2}$ | $ -\frac{ 1}{ \sqrt{ 2 }}$ | $ -\frac{1}{ 2}$ | 0 |
| cosθ | $ -\frac{ \sqrt{ 3 }}{ 2}$ | $ -\frac{ 1}{ \sqrt{ 2 }}$ | $ -\frac{1}{ 2}$ | 0 | $ \frac{1}{ 2}$ | $ \frac{ 1}{ \sqrt{ 2 }}$ | $ \frac{ \sqrt{ 3 }}{ 2}$ | 1 |
| tanθ | $ \frac{ 1}{ \sqrt{ 3 }}$ | 1 | $ \sqrt{ 3 }$ | なし | $ -\sqrt{ 3 }$ | -1 | $ -\frac{ 1}{ \sqrt{ 3 }}$ | 0 |
この表はとくに覚えなくても良いのですが、単位円をイメージして、角度と三角比を変換する「三角関数」に慣れておいてください。
三角関数の関係性
三角比の定義は
$ sinθ=\displaystyle\frac{ y }{ r }$、$ cosθ=\displaystyle\frac{ x}{ r }$、$ tanθ=\displaystyle\frac{ y }{ x }$
ですので、
$ y=rsinθ$
$ x=rcosθ$
と置き換えることができます。そして、tanθに代入すると、
$ \begin{eqnarray}tanθ&=&\displaystyle\frac{ y }{ x }\\\\&=&\displaystyle\frac{ rsinθ }{ rcosθ}\\\\&=&\displaystyle\frac{ sinθ }{ cosθ}\end{eqnarray}$
の関係が成り立ちます。また、三平方の定理は、$ r^2=x^2+y^2$ ですので、
$ \begin{eqnarray}r^2&=&(rcosθ)^2+(rsinθ)^2\\\\&=&r^2cos^2θ+r^2sin^2θ\end{eqnarray}$
$ sin^2θ+cos^2θ=1$
の関係が成り立ちます。
演習問題1
次の問題が解けますか?
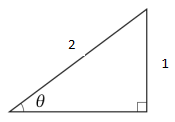
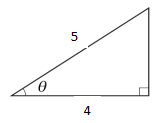
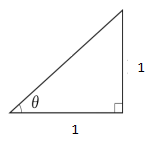
a 図の$ sinθ、cosθ、tanθ$を求めて下さい。
b $ 0°≦θ≦90°$のとき、次の問いがわかりますか?
① $ sinθ=\displaystyle\frac{ \sqrt{ 3 }}{ 2}$ のときの、$ cosθ$ ,$ tanθ$,$ θ$ の値
② $ cosθ=\displaystyle\frac{ \sqrt{ 3 }}{ 2}$ のとき、$ sinθ$ ,$ tanθ$,$ θ$ の値
③ $ tanθ=1$ のとき、$ sinθ$ ,$ cosθ$,$ θ$ の値
c 次の等式を満たすθの値がわかりますか?
① $sinθ=\displaystyle\frac{ 1 }{ 2}$
② $ sinθ=\displaystyle-\frac{ \sqrt{ 3 }}{ 2}$
③ $ cosθ=\displaystyle-\frac{1}{ 2}$
④ $ cosθ=-1$
⑤ $ tanθ=\displaystyle\frac{ 1}{ \sqrt{ 3 }}$
⑥ $ tanθ=0$
d $ sinθcosθ=1$ のとき次の値を求めてください。
① $ (sinθ+cosθ)^2$
② $ (sinθ-cosθ)^2$
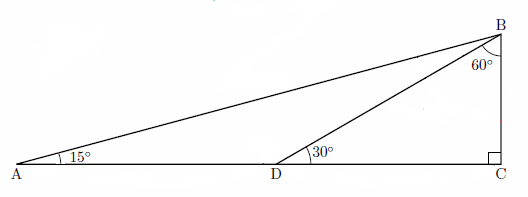
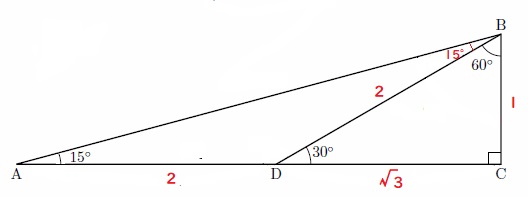
e 次の直角三角形を使って、$ sin15°、cos15°、tan15°$ を求めて下さい。
演習問題1の解答
aの解答
① $ sinθ=\displaystyle\frac{ 1 }{ 2}$
$ cosθ=\displaystyle\frac{ \sqrt{ 3 } }{ 2}$
$ tanθ=\displaystyle\frac{ 1 }{ \sqrt{ 3 }}$
② $ sinθ=\displaystyle\frac{ 3 }{ 5}$
$ cosθ=\displaystyle\frac{ 4 }{ 5}$
$ tanθ=\displaystyle\frac{ 3 }{ 4}$
③ $ sinθ=\displaystyle\frac{ 1}{ \sqrt{ 2 }}$
$ cosθ=\displaystyle\frac{ 1 }{ \sqrt{ 2 }}$
$ tanθ=1$
bの解答
① $ cosθ=\displaystyle\frac{ 1 }{ 2}$
$ tanθ={ \sqrt{ 3 }}$
$θ=60°$
② $ sinθ=\displaystyle\frac{ 1 }{ 2}$
$ tanθ=\displaystyle\frac{ 1 }{ \sqrt{ 3 }}$
$θ=30°$
③ $ sinθ=\displaystyle\frac{ 1}{ \sqrt{ 2 }}$
$ cosθ=\displaystyle\frac{ 1 }{ \sqrt{ 2 }}$
$θ=45°$
cの解答
①
$θ=30°,150°$
②
$θ=240°,300°$
③
$θ=120°,240°$
④
$θ=180°$
⑤
$θ=30°,210°$
⑥
$θ=0°,180°$
dの解答
①
$ (sinθ+cosθ)^2$
$ =sin^2θ+2sinθcosθ+cos^2θ$
$ =sin^2θ+cos^2θ+2sinθcosθ$
$ =1+2×1$
$ =3$
②
$ (sinθ-cosθ)^2$
$ =sin^2θ-2sinθcosθ+cos^2θ$
$ =sin^2θ+cos^2θ-2sinθcosθ$
$ =1-2×1$
$ =-1$
eの解答
直角三角形の辺の比と、二等辺三角形の性質より図のようになります。
ABの長さは三平方の定理より
$ \begin{eqnarray}AB^2&=&AC^2+BC^2\\
&=&(2+\sqrt{ 3 })^2+1\\
&=&4+4\sqrt{ 3 }+3+1\\
&=&8+4\sqrt{ 3 }\\
&=&8+2\sqrt{ 12 }\\
&=&(\sqrt{ 6 }+\sqrt{ 2 })^2\end{eqnarray}$
$ AB=\sqrt{ 6 }+\sqrt{ 2 }$
$ \begin{eqnarray}sin15°&=&\displaystyle\frac{ 1 }{ \sqrt{ 6 }+\sqrt{ 2 }}\\\\
&=&\displaystyle\frac{ \sqrt{ 6 }-\sqrt{ 2 } }{ (\sqrt{ 6 }+\sqrt{ 2 })(\sqrt{ 6 }-\sqrt{ 2 })}\\\\
&=&\displaystyle\frac{ \sqrt{ 6 }-\sqrt{ 2 } }{ 4}\end{eqnarray}$
$ \begin{eqnarray}cos15°&=&\displaystyle\frac{ 2+\sqrt{ 3 } }{ \sqrt{ 6 }+\sqrt{ 2 }}\\\\
&=&\displaystyle\frac{ (2+\sqrt{ 3 } )(\sqrt{ 6 }-\sqrt{ 2 } )}{ (\sqrt{ 6 }+\sqrt{ 2 })(\sqrt{ 6 }-\sqrt{ 2 })}\\\\
&=&\displaystyle\frac{ \sqrt{ 6 }+\sqrt{ 2 } }{ 4}\end{eqnarray}$
$ \begin{eqnarray}tan15°&=&\displaystyle\frac{ 1 }{ 2+\sqrt{ 3 }}\\\\
&=&\displaystyle\frac{ (2-\sqrt{ 3 } )}{ (2+\sqrt{ 3 })(2-\sqrt{ 3 })}\\\\
&=& 2-\sqrt{ 3}\end{eqnarray}$
電験三種の計算で使う三角関数
弧度法について
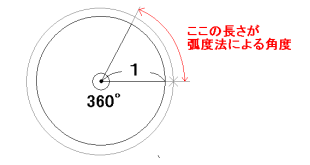
弧度法とは角度を表す概念です。扇を描いたときの弧の長さを基準に角の大きさを考えるという方法で、円を1周すると$ 2π$ラジアン(rad)とする測り方です。
度数 ⇔ ラジアン変換の公式
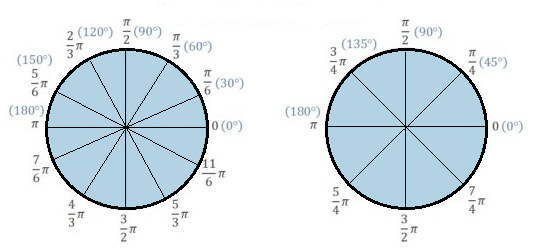
$ θ(°)=θ×\displaystyle\frac{π}{180°}$(rad)
象限と三角関数の値の正負について
象限とは、x軸とy軸で構成される座標平面において、下の図に示すような「領域」のことをいいます。各象限は x , y の符号が決まっていますので,三角関数の符号も定まります。
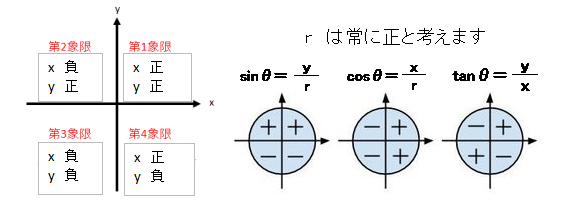
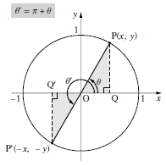
三角関数の対称性と移動性について
単位円と三角関数の関係を検討することにより、以下のような性質を導くことができます。公式を覚えるのは大変なので、単位円から導きだせるようにしておいてください。
加法定理
加法定理は電顕3種では数年に1度、理論で出題される二つの電力計を使った計算問題で使う程度ですが、一応載せておきます。加法定理を覚えていると、この公式を変形させて様々な三角関数の計算ができるようになります。電験3種の勉強で出てきた時に覚えてもらえればと思います。
$ sin(α±β)=sinαcosβ±cosαsinβ$
$ cos(α±β)=cosαcosβ̠∓sinαsinβ$
逆三角関数
まず関数とは、「2つの変数x、yについて,xの値を決めるとそれに応じてyの値がただ1つ定まるとき,y は x の関数」となります。つまり、値を変換するルールのことです。そして、「これは関数です。」と表わすための記号として、$ f$( functionのf )を使います。$ f(x)=$ の(x) は,「 xの関数 」ということを示しています。
逆関数とは、xとyの「役割」を入れ替え,値を変換するルールを逆から見た関数のことです。「これは逆関数です。」と表わすための記号として、$ f^{ -1}$ (読み:インバース)を使います。$ f^{ -1}(x)=$ の(x) は,「xの逆関数」ということを示しています。
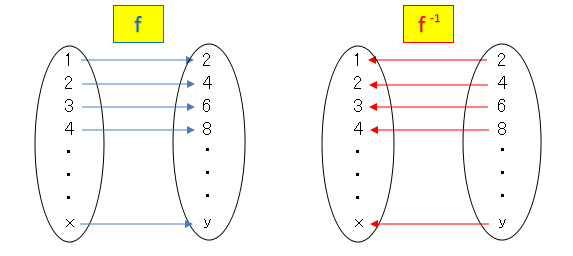
上図の左側を関数で表示しますと、「$ f(x)=2x$」となります。この書き方は関数を扱う際の正式な書き方なのですが、$ f(x)$と書くのも面倒なので、方程式に当てはめて「$ y=2x$ ・・・ ①」と書きます。
逆関数とは、xとyの「役割」を入れ替え,値を変換するルールを逆から見た関数のことですから、①式に当てはめてみると、「$ x=2y$ ⇒ $ y=\frac{x}{2}$」となります。上図の右側をxの関数として表示しますと、「$ f^{ -1}(x)=\frac{x}{2}$」となります。これが逆関数の考え方です。
逆関数を三角関数に当てはめて考えてみます。例えば、$ sinθ=\frac{ \sqrt{ 3 }}{ 2}$を例に取りますと、逆三角関数は
$ sin^{-1}\displaystyle\frac{ \sqrt{ 3 }}{ 2}=θ$ もしくは $ arcsin\displaystyle\frac{ \sqrt{ 3 }}{ 2}=θ$ (読み:アークサイン)
と書きます。$ cosθ$ や $ tanθ$も同様です。式からもわかるとおり、逆三角関数は三角比から角度を求めるときに使います。
演習問題2
次の問題が解けますか?
a 次の角を弧度法で表してください。
① 60°
② 210°
③ 3°
b 0≦θ<2πのとき次の値を求めてください。
① $ sinθ=\displaystyle-\frac{ 1 }{ 2}$
② $ cosθ=\displaystyle\frac{ 1 }{ \sqrt{ 2 } }$
c 次の値を求めてください。
① $ sin^{ -1 }\displaystyle\frac{ \sqrt{ 3 } }{ 2}$
② $ cos^{ -1 }\displaystyle(-\frac{ 1 }{ 2})$
演習問題2の解答
aの解答
① $ 60×\displaystyle\frac{ π }{ 180}=\displaystyle\frac{ π }{ 3}$
② $ 210×\displaystyle\frac{ π }{ 180}=\displaystyle\frac{ 7π }{ 6}$
③ $ 3×\displaystyle\frac{ π }{ 180}=\displaystyle\frac{ π }{ 60}$
bの解答
① $ θ=\displaystyle\frac{ 7π }{ 6}、\displaystyle\frac{ 11π }{ 6}$
② $ θ=\displaystyle\frac{ π }{ 4}、\displaystyle\frac{ 7π }{ 4}$
cの解答
① $ sin^{ -1 }\displaystyle\frac{ \sqrt{ 3 } }{ 2}=\displaystyle\frac{ π }{ 3}$
② $ cos^{ -1 }\displaystyle(-\frac{ 1 }{ 2})=\displaystyle\frac{ 2π }{ 3}$