水力発電所と揚水発電所の出力

このページでは、水力発電所と揚水発電所の出力について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の電力科目の試験で、実際に出題された、水力発電所と揚水発電所の出力の過去問題も解説しています。

水力発電所の出力
揚水発電所の出力
1. 揚水時に電動機が消費する電力
2. 揚水発電所の総合効率
比速度
電験三種－電力（水力発電）過去問題

水力発電所の出力

落差とは？

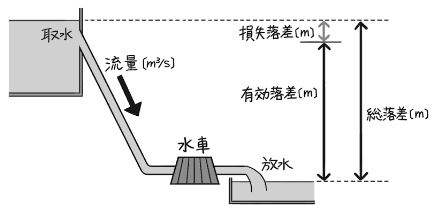
水力発電所の出力は、「落差」と「流量」に関係しています。落差は、水車が動力として利用する水位の差のことで、取水口から放水口までの水位差を「総落差」、総落差から損失分を差し引いた落差を「有効落差」といいます。

有効落差($H$)=総落差($H_G$)－損失落差($h_1$)

水力発電所の理論出力

水力発電所の理論出力 P₀は、使用水量を Q［m³/s］、有効落差を H［m］とすると、次の式で求めることができます。

$P_0=9.8QH $［kW］

質量 m［kg］の水が高さ H［m］の位置にあるときのエネルギー W［J］は、重力加速度を9.8［m/s²］とすると、

$W=9.8mH $［J］

となります。仕事量は単位時間当たりのエネルギーですので、水が1秒間に行う仕事量は

$P=9.8mH $［W］

となります。１m³の水の重さは1000［kg］ですので、Q［m³］の水の質量は 1000Q［kg］です。したがって Q［m³］の水が落下する際の仕事量 P は、

$P=9.8×1000QH［W］=9.8QH［kW］$

となり、水力発電所の理論出力の式と同じになります。

水車出力

水力発電所の理論出力から水車で生じる摩擦などの損失を差し引いた出力を水車出力 P_w といいます。水車効率を η_w［%］（ηの読み：イータ）とすると、次の式で求めることができます。

$P_w=9.8QHη_w$［kW］

発電機出力

発電機は水車と直結されていますので、水車の出力は発電機の入力となります。発電機効率を η_G［%］とすると、発電機出力 P は次の式で求めることができます。

$P_G=9.8QHη_wη_G$［kW］

尚、$η=η_wη_G$ を総合効率といいます。

揚水発電所の出力

揚水発電所は夜間の軽負荷時や豊水期などに発生する余剰電力を利用して、ポンプで貯水池に揚水し、ピーク時に貯水を発電に利用する発電所です。

余剰電力を位置エネルギーに変換して蓄えておき、必要に応じて再び電気エネルギーに変換する蓄電設備の一種として考えることができます。

揚水時に電動機が消費する電力

揚水発電所の揚水時に電動機が必要な電力 P_P は次の式で求めることができます。

$P_P=\displaystyle \frac{ 9.8Q_PH }{ η_Pη_M}$
　
Q_P：揚水量［m³/s］
H：有効揚程［ｍ］
η_P：ポンプ効率［%］
η_M：電動機効率［%］

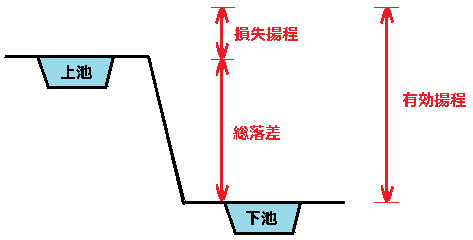
有効揚程 H［ｍ］はポンプで水をくみ上げる高さのことです。

有効揚程(H)＝総落差(H₀)+損失落差(h_L)

となります。

揚水発電所の総合効率

揚水のための必要な電力（揚水電力）に対する発電時の出力（発電機出力）の割合を求めると、揚水発電の総合効率が算出できます。

$総合効率=\displaystyle \frac{ 発電機出力P_G }{ 揚水電力P_P}×100$［%］

比速度

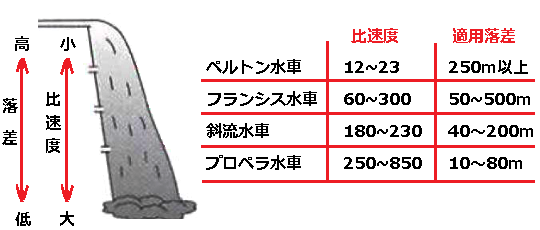
比速度とは、実物の水車と幾何学的に相似な模型水車が、単位落差１mにおいて単位出力１kWを発生するときの１分間の回転数のことをいいます。

落差が高い発電所では、水車の比速度が大きいと回転数が大きくなりすぎるため、比速度の小さな水車が適します。落差が低い発電所では、回転数を得るために比速度の大きな水車が適します。

水車の定格速度を N［min^-1］、最大出力を P［kW］、有効落差を H［m］とすれば、比速度 N_S は次の式で求めることができます。

$N_S=N\displaystyle \frac{ P^{\frac{1}{2}} }{ H^{\frac{5}{4}}}$［ｍ・kW］

電験三種－電力（水力発電）過去問題

1998年（平成10年）問11

発電電動機1台の揚水発電所があり、揚水運転しているとき、上池水位が標高 1300［m］、下池水位が標高 810［m］で発電電動機入力が 300［MW］である。このときの揚水量[m³/s]の値として、正しいものは次のうちどれか。ただし、ポンプ効率は 85［%］、電動機効率は 98［%］、損失水頭は 10［m］とする。

(1) 20　(2) 31　(3) 51　(4) 60　(5) 71

1998年（平成10年）問11　過去問解説

揚水発電所の揚水時に電動機が必要な電力 P_P は、

$P_P=\displaystyle \frac{ 9.8Q_PH }{ η_Pη_M}$

$300×10^3=\displaystyle \frac{ 9.8Q_P(1300-810+10) }{ 0.85×0.98}$

$Q_P=51［m^3/s］$

答え (3)

2000年（平成12年）問2

水車の比速度とは、その水車と幾何学的に相似なもう一つの水車を仮想し、この仮想水車を1［m］の(　ア　)のもとで相似な状態で運転させ、1［kW］の出力を発生するような(　イ　)としたときの、その仮想水車の回転速度［r/min］をいう。
水車の比速度 n_S［m・kW］は水車出力を P［kW］、有効落差 H［m］、回転速度を n［r/min］とすれば、次の式で表される。

$$n_S=n×\displaystyle\frac{ (　ウ　)^{\frac{ 1 }{ 2 }} }{ (　エ　)^{\frac{ 5 }{ 4 }} }$$

ただし、水車出力Pはペルトン水車ではノズル1個当たり、(　オ　)水車ではランナ1個当たりの出力である。
上記の記述中の空白の(ア)，(イ)，(ウ)，(エ)及び(オ)に記入する記号又は字句として、正しいものを組み合わせたのは次のうちどれか。

	（ア）	（イ）	（ウ）	（エ）	（オ）
（１）	落差	寸法	P	H	反動
（２）	範囲	落差	H	P	衝動
（３）	落差	寸法	H	P	衝動
（４）	落差	寸法	H	P	反動
（５）	範囲	落差	P	H	衝動

2000年（平成12年）問2　過去問解説

水車の比速度とは、その水車と幾何学的に相似なもう一つの水車を仮想し、この仮想水車を1［m］の(　落差　)のもとで相似な状態で運転させ、1［kW］の出力を発生するような(　寸法　)としたときの、その仮想水車の回転速度［r/min］をいう。
水車の比速度 n_S［m・kW］は水車出力を P［kW］、有効落差 H［m］、回転速度を n［r/min］とすれば、次の式で表される。

$$n_S=n×\displaystyle\frac{ (　P　)^{\frac{ 1 }{ 2 }} }{ (　H　)^{\frac{ 5 }{ 4 }} }$$

ただし、水車出力Pはペルトン水車ではノズル1個当たり、(　反動　)水車ではランナ1個当たりの出力である。

答え（１）

2002年（平成14年）問1

最大使用水量 15［m³/s］、総落差 110［ｍ］、損失落差 10［ｍ］の水力発電所がある。年平均使用水量を最大使用水量の 60［％］とするとき、この発電所の年間発電電力量［GW･h］と値として、最も近いのは次のうちどれか。ただし、発電所総合効率は 90［％］一定とする。

(1) 7.1　(2) 70　(3) 76　(4) 84　(5) 94

2002年（平成14年）問1　過去問解説

総合効率を η としたとき、発電機出力 P_G は、

$P_G=9.8QHη［kW］$

年間発電電力量は、

$P_G=9.8×15×0.6×(110-10)×0.9×365×24≒70［GW･h］$

答え（２）

2009年（平成21年）問1

水力発電所において、有効落差 100［m］、水車効率 92［％］、発電機効率 94［％］、定格出力 2500［kw］の水車発電機が 80［％］負荷で運転している。このときの流量［m³/s］の値として、最も近いのは次のうちどれか。

(1) 1.76　(2) 2.36　(3) 3.69　(4) 17.3　(5) 23.1

2009年（平成21年）問1　過去問解説

発電機出力 P_G は、

$P_G=9.8QHη_wη_G［kW］$

水車発電機が 80［％］負荷で運転しているので、

$2500×0.8=9.8Q×100×0.92×0.98$

$Q≒2.36［m^3/s］$

答え（２）

2012年（平成24年）問1

次の文章は、水力発電の理論式に関する記述である。
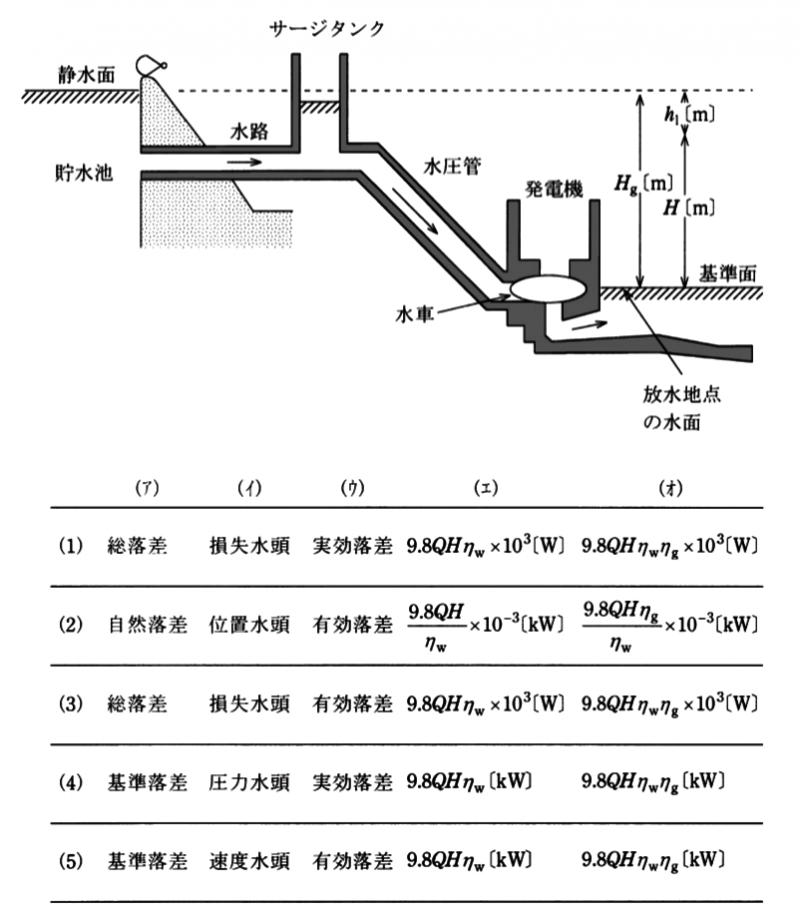
図に示すように、放水地点の水面を基準面とすれば、基準面から貯水池の静水面までの高さ H_g［m］を一般に（　ア　）という。また、水路や水圧管の壁と水との摩擦によるエネルギー損失に相当する高さ h₁ ［m］を（　イ　）という。さらに、H_gと h₁ の差 H － H_g － h₁ を一般に（　ウ　）という。
いま、Q ［m³/s］の水が水車に流れ込み、水車の効率を η_w とすれば、水車出力を P_w は（　エ　）になる。さらに、発電機の効率を η_g とすれば、発電機出力 P は（　オ　）になる。ただし、重力加速度は 9.8 ［m/s²］とする。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

2012年（平成24年）問1　過去問解説

図に示すように、放水地点の水面を基準面とすれば、基準面から貯水池の静水面までの高さ H_g［m］を一般に（　総落差　）という。また、水路や水圧管の壁と水との摩擦によるエネルギー損失に相当する高さ h₁ ［m］を（　損失水頭　）という。さらに、H_gと h₁ の差 H － H_g － h₁ を一般に（　有効落差　）という。
いま、Q ［m³/s］の水が水車に流れ込み、水車の効率を η_w とすれば、水車出力を P_w は（　$9.8QHη_w×10^3$［W］　）になる。さらに、発電機の効率を η_g とすれば、発電機出力 P は（　$9.8QHη_wη_g×10^3$［W］　）になる。ただし、重力加速度は 9.8 ［m/s²］とする。

答え (3)

2014年（平成26年）問15

ペルトン水車を1台もつ水力発電所がある。図に示すように、水車の中心線上に位置する鉄管のA点において圧力 p［Pa］と流速 v［m/s］を測ったところ、それぞれ 3000kPa、5.3 m/sの値を得た。また、このA点の鉄管断面は内径 1.2 mの円である。次の(a)及び(b)の問に答えよ。
ただし、A点における全水頭 H［m］は位置水頭、圧力水頭、速度水頭の総和として $ h+\displaystyle\frac{ p }{ ρg }+\displaystyle\frac{ v^2 }{ 2g }$より計算できるが、位置水頭 hはA点が水車中心線上に位置することから無視できるものとする。また、重力加速度は g=9.8m/s²、水の密度は ρ=1000kg/m³ とする。

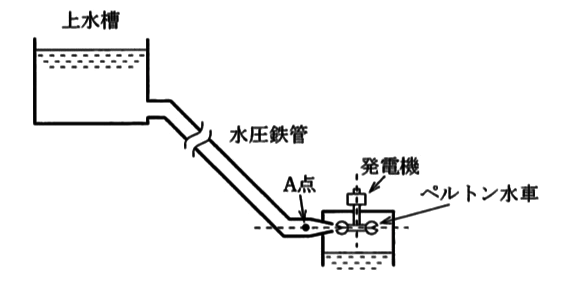
(a)　ペルトン水車の流量の値［m³/s］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 3　(2 )4　(3) 5　(4) 6　(5) 7

(b)　水車出力の値［kW］として、最も近いものを次の(1)～(5)のうちから一つ選べ。ただし、A点から水車までの水路損失は無視できるものとし、また水車効率は 88.5%とする。

(1) 13000　(2) 14000　(3) 15000　(4) 16000　(5)17000

2014年（平成26年）問15　過去問解説

(a) の解説

流量 Qは、Q=断面積×速度なので、

$Q=0.6^2×π×5.3≒5.99［m^3/s］$

答え (4)

(b) の解説

$H= h+\displaystyle\frac{ p }{ ρg }+\displaystyle\frac{ v^2 }{ 2g }$

$H=0+\displaystyle\frac{ 3000×10^3 }{ 1000×9.8 }+\displaystyle\frac{ 5.3^2 }{ 2×9.8 }≒307［m］$

水車出力 P_w は、

$P_w=9.8QHη_w$

$P_w=9.8×5.99×307×0.885≒15900［kW］$

答え (4)

2015年（平成27年）問1

水力発電所の理論水力 Pは位置エネルギーの式から P=ρgQHと表される。ここで H［m］は有効落差、Q ［m³/s］は流量、gは重力加速度=9.8m/s²、ρ は水の密度=1000kg/m³ である。以下に理論水力 P の単位を検証することとする。なお、Paは「パスカル」、Nは「ニュートン」、Wは「ワット」、Jは「ジュール」である。
P=ρgQH の単位は ρ、g、Q、H の単位の積であるから、kg/m³・m/s²・m³/s・m となる。これを変形すると、（　ア　）・m/sとなるが、（　ア　）は力の単位（　イ　）と等しい。すなわち P=ρgQH の単位は（　イ　）・m/sとなる。ここで（　イ　）・mは仕事（エネルギー）の単位である（　ウ　）と等しいことから P=ρgQH の単位は（　ウ　）/sと表せ、これは仕事率（動力）の単位である（　エ　）と等しい。ゆえに、理論水力 P=ρgQH の単位は（　エ　）となるが、重力加速度 g=9.8m/s² と水の密度 ρ=1000kg/m³ の数値 9.8 と 1000 を考慮すると p=9.8QH［（　オ　）］と表せる。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

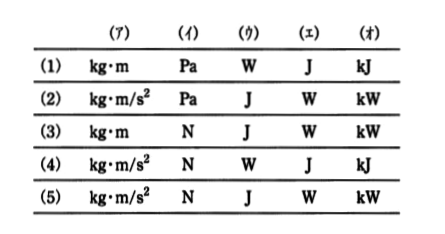
2015年（平成27年）問1　過去問解説

水力発電所の理論水力 Pは位置エネルギーの式から P=ρgQHと表される。ここで H［m］は有効落差、Q ［m3/s］は流量、gは重力加速度=9.8m/s2、ρ は水の密度=1000kg/m3 である。以下に理論水力 P の単位を検証することとする。なお、Paは「パスカル」、Nは「ニュートン」、Wは「ワット」、Jは「ジュール」である。
P=ρgQH の単位は ρ、g、Q、H の単位の積であるから、kg/m3・m/s2・m3/s・m となる。これを変形すると、（　kg・m/s²　）・m/sとなるが、（　kg・m/s²　）は力の単位（　N　）と等しい。すなわち P=ρgQH の単位は（　N　）・m/sとなる。ここで（　N　）・mは仕事（エネルギー）の単位である（　J　）と等しいことから P=ρgQH の単位は（　 J　）/sと表せ、これは仕事率（動力）の単位である（　W　）と等しい。ゆえに、理論水力 P=ρgQH の単位は（　W　）となるが、重力加速度 g=9.8m/s2 と水の密度 ρ=1000kg/m3 の数値 9.8 と 1000 を考慮すると p=9.8QH［（　kW　）］と表せる。

答え（５）

2016年（平成28年）問1

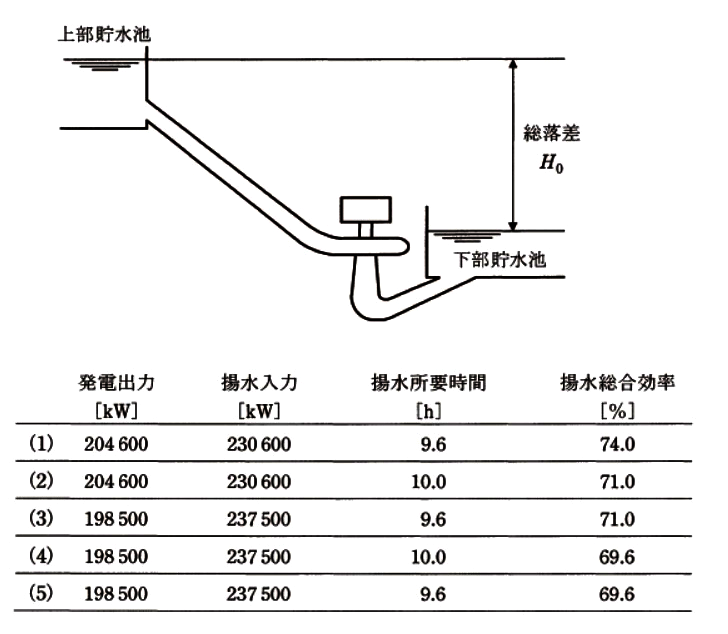
下記の諸元の揚水発電所を、運転中の総落差が変わらず、発電出力、揚水入力ともに一定で運転するものと仮定する。この揚水発電所における発電出力の値［kW］、揚水入力の値［kW］、揚水所要時間の値［h］及び
揚水総合効率の値［%］として、最も近い値の組合せを次の(1)～(5)のうちから一つ選べ。

揚水発電所の諸元

総落差	H₀=400m
発電損失水頭	h_G=H₀の3%
揚水損失水頭	h_P=H₀の3%
発電使用水量	Q_G=60m³/s
揚水量	Q_P=50m³/s
発電運転時の効率	発電機効率 η_G×水車効率η_T=87%
ポンプ運転時の効率	電動機効率 η_M×ポンプ効率η_P=85%
発電運転時間	T_G=8h