第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される単相交流の直列回路について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された単相交流の直列回路の過去問題も解説しています。
$R,L,C$ 単独回路
抵抗 $R$ が単独の交流回路
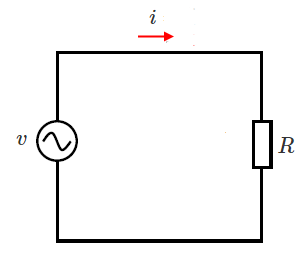
抵抗 $R$ の両端に電圧 $v=\sqrt{2}Vsinωt$[V]の電圧を加えます。流れる電流を $i$[A]、電流の実効値を $I$[A]とすると、次のようになります。
$i =\sqrt{2}\displaystyle \frac{V}{ R }sinωt$[A]
$ I = \displaystyle \frac{ V}{ R }$ [A]
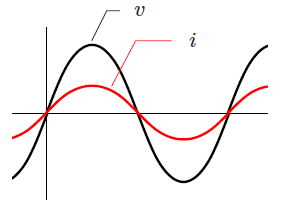
交流電源 $v$ と抵抗 $R$ だけの回路では、電圧 $v$ と 電流 $i$ は「同相」になります。
交流回路にコイルやコンデンサが入ると、電圧と電流に位相差が生じますが、電源と抵抗だけの回路では位相差 は生じません。
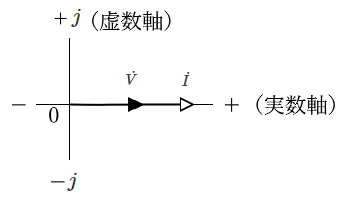
電圧 $v$[V],電流 $i$[A]を平面ベクトル $\dot{V}$[V],$\dot{I}$[A]で表します。
電流ベクトル $\dot{I}$ と電圧ベクトル $\dot{V}$ は、同じ方向になります。
$\dot{I}= \displaystyle \frac{\dot{ V}}{ R }$[A]
コイル(インダクタ) $L$ が単独の交流回路
コイル(インダクタ)は素子を流れる電流 $i $[A]と素子が発生する磁束 $ϕ$[Wb]が比例する素子です。
$ϕ = Li$
比例定数 $L$ を「インダクタンス」(単位:H 読み[ヘンリー])といいます。インダクタンスが $L$ であるコイルのことを、「コイル $L$ 」と呼びます。
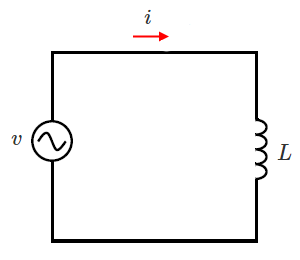
コイル $L$ の両端に電圧 $v=\sqrt{2}Vsinωt$[V]の電圧を加えます。流れる電流を $i$[A]、電流の実効値を $I$[A]とすると、次のようになります。
$i =\sqrt{2}\displaystyle \frac{ V}{ ωL }sin(ωt-\displaystyle \frac{ π}{ 2 })$[A]
$ I = \displaystyle \frac{ V}{ ωL }$ [A]
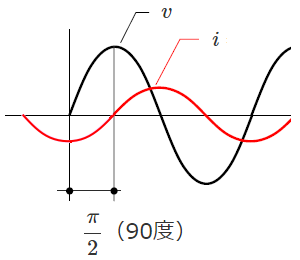
コイルの入っている交流回路では、電圧の位相と電流の位相に差が発生します。
電圧の位相に比べて、電流の位相が遅れることを「遅れ」と表現します。
交流電源とコイルだけの回路では $\displaystyle \frac{ π}{ 2 }$(90度)の遅れになります。
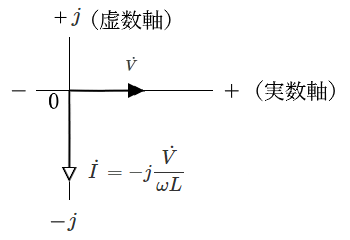
電圧 $v$[V],電流 $i$[A]を平面ベクトル $\dot{V}$[V],$\dot{I}$[A]で表します。
電流ベクトル $\dot{I}$ は、電圧ベクトル $\dot{V}$ より $\displaystyle \frac{ π}{ 2 }$(90度)遅れます。
$\dot{I}= \displaystyle \frac{\dot{ V}}{ jωL }= -j\displaystyle \frac{\dot{ V}}{ωL }$[A]
コンデンサ(キャパシタ) $C$ が単独の交流回路
コンデンサ(キャパシタ)は素子に蓄えられている電荷 $q$[C] が素子の端子間電圧 $v$[V]に比例する素子です。
$ q=Cv $
比例定数 $C$ を「キャパシタンス又は静電容量」(単位:F 読み[ファラド])といいます。静電容量が $C$ であるコ ンデンサのことを、「コンデンサ $C$」と呼びます。
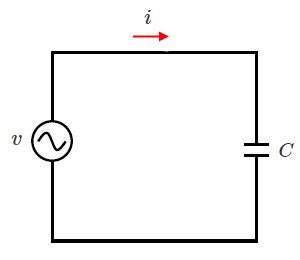
コンデンサ $C$ の両端に電圧 $v=\sqrt{2}Vsinωt$[V]の電圧を加えます。流れる電流を $i$[A] 、電流の実効値を $I$[A]とすると、次のようになります。
$\begin{eqnarray}i &=&\sqrt{2}×\displaystyle \frac{ V}{ \displaystyle \frac{ 1}{ ωC } }sin(ωt+\displaystyle \frac{ π}{ 2 })\\\\&=&\sqrt{2}ωCVsin(ωt+\displaystyle \frac{ π}{ 2 })[A]\end{eqnarray}$
$ I = ωCV$ [A]
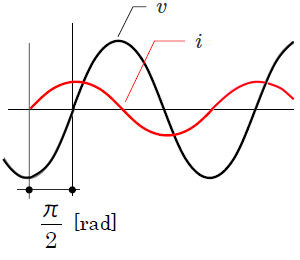
コンデンサの入っている交流回路では、電圧の位相と電流の位相に差が発生します。
電圧の位相に比べて、電流の位相が進むことを「進み」と表現します。
交流電源とコイルだけの回路では $\displaystyle \frac{ π}{ 2 }$(90度)の進みになります。
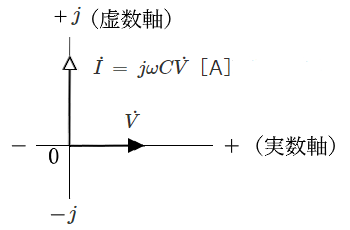
電圧 $v$[V],電流 $i$[A]を平面ベクトル $\dot{V}$[V],$\dot{I}$[A]で表します。
電流ベクトル $\dot{I}$ は、電圧ベクトル $\dot{V}$ より $\displaystyle \frac{ π}{ 2 }$(90度)進みます。
$\dot{I}= \displaystyle \frac{\dot{ V}}{ \displaystyle \frac{ 1}{ jωC } }= jωC\dot{ V}$[A]
誘導性リアクタンスと容量性リアクタンス
コイルとコンデンサにおいて、電圧と電流の実効値に注目すると、$ωL$ と $\displaystyle \frac{ 1 }{ ωC }$ は抵抗と同様の働きをしていることが分かります。これらは、「誘導性リアクタンス $X_L$」 と「容量性リアクタンス $X_C$」 と定義されています。どちらも単位はオーム[Ω]です。
誘導性リアクタンスと容量性リアクタンス
誘導性リアクタンス:$X_L=ωL=2πfL$[Ω]
容量性リアクタンス:$X_C=\displaystyle \frac{ 1 }{ ωC }=\displaystyle \frac{ 1 }{ 2πfC }$ [Ω]
インピーダンスとアドミタンス
インピーダンス
交流回路で素子の両端の電圧を $\dot{V}$[V]、素子を流れる電流を $\dot{I}$[A]とするとき、「インピーダンス $Z$[Ω]」と呼ばれる量が定義されています。
インピーダンス $Z$ の定義式:$Z = \displaystyle \frac{ \dot{V} }{ \dot{I} } $
この関係式は、直流回路におけるオームの法則と同じ形で、抵抗 $R$ をインピーダンス $Z$ に置き換えたものです。ただし、一般的にはインピーダンスは複素数になりますので、計算は直流回路に比べて複雑になります。各基本素子のインピーダンスは次のとおりになります。
抵抗のインピーダンス
$Z=R$
コイルのインピーダンス
$Z=jωL=jX_L$
コンデンサのインピーダンス
$Z = \displaystyle \frac{ 1 }{ jωC } =-jX_C$
インピーダンス三角形
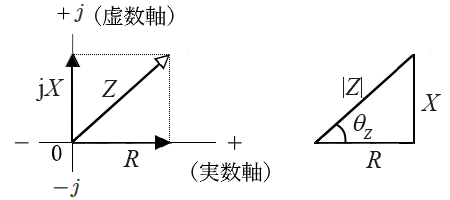
インピーダンス $Z$ をベクトル図で表すと、$R$ が抵抗分、$X$ がリアクタンス分になります。リアクタンス分が正のときは誘導性で、負のときは容量性といいます。
インピーダンス $Z$ を、$Z=|Z|∠θ_Z$ とすると、$|Z|$ をインピーダンスの大きさ、$θ_Z$ をインピーダンス角といい、次のとおりになります。
インピーダンス三角形
$|Z|=\sqrt{R^2+X^2}$
$tanθ_Z= \displaystyle \frac{ X }{ R } $
アドミタンス
インピーダンス $Z$ の逆数を「アドミタンス $Y$(単位:S 読み[ジーメンス])」 といいます。インピーダンスと同様に、アドミタンスも複素数になります。
アドミタンス $Y$ の定義式:$Y=\displaystyle \frac{ 1}{ Z } = \displaystyle \frac{\dot{I}}{ \dot{V}} $
各基本素子のアドミタンスは次のとおりになります
抵抗のアドミタンス
$Y=\displaystyle \frac{ 1}{R } $
コイルのアドミタンス
$Y=\displaystyle \frac{ 1}{ jωL } =-jX_L$
コンデンサのアドミタンス
$Y=jωC=jX_C$
アドミタンス三角形
アドミタンス $Y$ をベクトル図で表すと、$G$ がコンダクタンス分、$B$ がサセプタンス分といいます。サセプタンス分が正のときは容量性で、負のときは誘導性になります。
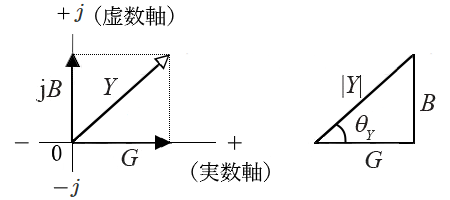
アドミタンス $Y$ を、$Y=|Y|∠θ_Y$ とすると、$|Y|$ をアドミタンスの大きさ、$θ_Y$ をアドミタンス角といい、次のとおりになります。
アドミタンス三角形
$|Y|=\sqrt{G^2+B^2}$
$tanθ_Y= \displaystyle \frac{ B }{ G } $
交流の直列回路
合成インピーダンス
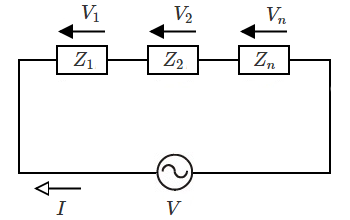
図のようなインピーダンス $Z_1$,$Z_2$,… $Z_n$ が直列に接続された回路の合成インピーダンス $\dot{Z}$ は次のようになります。
$\dot{Z}=\dot{Z_1}+\dot{Z_2}+…\dot{Z_n}$
合成インピーダンスはベクトル計算になります。
$RL$ 直列回路
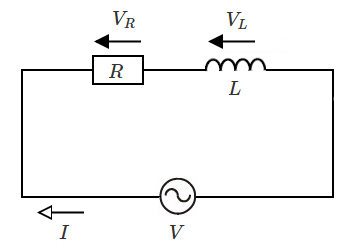
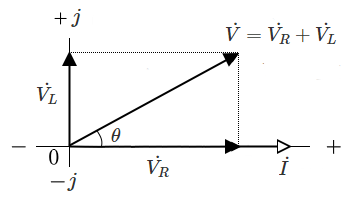
電流 $I$ を基準としたフェーザ図は次のようになります。
電圧と電流の関係式
$\dot{V_R}=R\dot{I}$
$\dot{V_L}=jωL\dot{I}$
$\dot{V}=\dot{V_R}+\dot{V_L}=(R+jωL)\dot{I}$
$θ=tan^{-1} \displaystyle \frac{ V_L }{ V_R } $
誘導性リアクタンスを $X_L$[Ω]、インピーダンス $\dot{Z}$ の大きさを $Z$[Ω]とすると、抵抗 $R$ とコイル $L$ からなる直列回路は、次のような関係式が成り立ちます。
$RL$ 直列回路の関係式
$X_L=ωL=2πfL$
$V_R=IR$,$V_L=IX_L$
$V=\sqrt{{V_R}^2+{V_L}^2}=I\sqrt{{R}^2+{X_L}^2}$
$Z= \displaystyle \frac{ V }{ I}= \sqrt{R^2+{X_L}^2}= \sqrt{R^2+(ωL)^2}$
$θ=tan^{-1} \displaystyle \frac{ V_L }{ V_R }=tan^{-1} \displaystyle \frac{ X_L }{ R } $
$X_L$[Ω]:誘導性リアクタンス
$V_R$[V],$V_L$[V]:各電圧
$V$[V]:全電圧
$Z$[Ω]:インピーダンス
$θ$[rad]:位相差
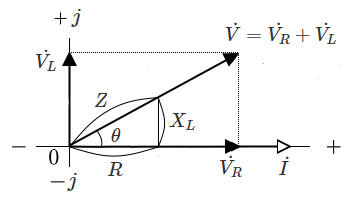
インピーダンス三角形は、電流 $I$ を基準とした電圧のフェーザ図と相似になります。
$RC$ 直列回路
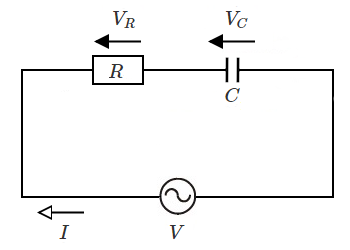
電流 $I$ を基準としたフェーザ図は次のようになります。
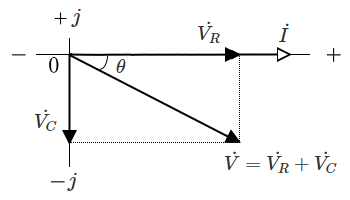
電圧と電流の関係式
$\dot{V_R}=R\dot{I}$
$\dot{V_C}= \displaystyle \frac{ \dot{I} }{ jωC }=-j \displaystyle \frac{ \dot{I} }{ ωC }$
$\dot{V}=\dot{V_R}+\dot{V_C}=(R-j \displaystyle \frac{ 1}{ ωC })\dot{I} $
$θ=tan^{-1} \displaystyle \frac{ V_C }{ V_R } $
容量性リアクタンスを $X_C$[Ω]、インピーダンス $\dot{Z}$ の大きさを $Z$[Ω]とすると、抵抗 $R$ とコンデンサ $C$ からなる直列回路は、次のような関係式が成り立ちます。
$RC$ 直列回路の関係式
$X_C=\displaystyle \frac{ 1}{ωC}=\displaystyle \frac{ 1}{2πfC}$
$V_R=IR$,$V_C=IX_C$
$V=\sqrt{{V_R}^2+{V_C}^2}=I\sqrt{{R}^2+{X_C}^2}$
$Z= \displaystyle \frac{ V }{ I}= \sqrt{R^2+{X_C}^2}=\sqrt{R^2+(\frac{ 1}{ωC})^2}$
$θ=tan^{-1} \displaystyle \frac{ V_C }{ V_R }=tan^{-1} \displaystyle \frac{ X_C }{ R } $
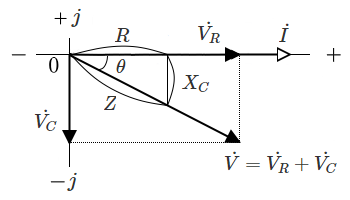
$X_C$[Ω]:容量性リアクタンス
$V_R$[V],$V_C$[V]:各電圧
$V$[V]:全電圧
$Z$[Ω]:インピーダンス
$θ$[rad]:位相差
インピーダンス三角形は、電流 $I$ を基準とした電圧のフェーザ図と相似になります。
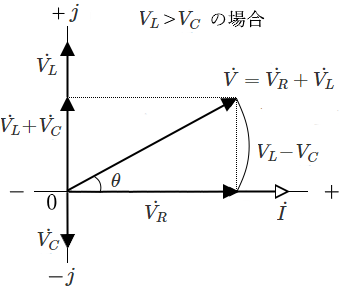
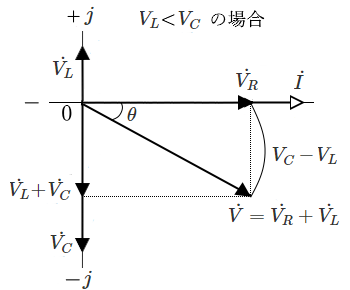
$RLC$ 直列回路
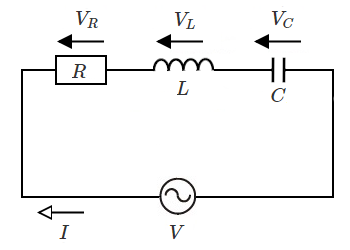
電流 $I$ を基準としたフェーザ図は次のようになります。
電圧と電流の関係式
$\dot{V_R}=R\dot{I}$
$\dot{V_L}=jωL\dot{I}$
$\dot{V_C}= \displaystyle \frac{ \dot{I} }{ jωC }=-j \displaystyle \frac{ \dot{I} }{ ωC }$
$\dot{V}=\dot{V_R}+\dot{V_L}+\dot{V_C}=\left(R+j(ωL-\displaystyle \frac{1}{ωC})
\right)\dot{I}$
誘導性リアクタンスを $X_L$[Ω]、容量性リアクタンスを $X_C$[Ω]、インピーダンス $\dot{Z}$ の大きさを $Z$[Ω]とすると、抵抗 $R$ とコンデンサ $C$ からなる直列回路は、次のような関係式が成り立ちます。
$RLC$ 直列回路の関係式
$X_L=ωL=2πfL$
$X_C=\displaystyle \frac{ 1}{ωC}=\displaystyle \frac{ 1}{2πfC}$
$V_R=IR$,$V_L=IX_L$,$V_C=IX_C$
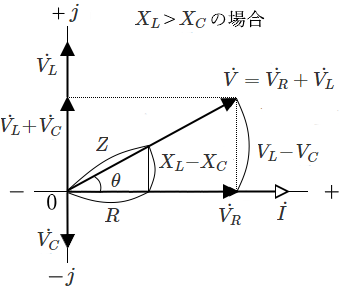
【$X_L>X_C$ の場合】
$V=\sqrt{{V_R}^2+(V_L-V_C)^2}=I\sqrt{R^2+(X_L-X_C)^2}$
$\begin{eqnarray}Z= \displaystyle \frac{ V }{ I}&=& \sqrt{R^2+(X_L-X_C)^2}\\&=&\displaystyle \sqrt{R^2+(ωL-\frac{ 1 }{ ωC })^2}\end{eqnarray}$
$θ=tan^{-1} \displaystyle \frac{ V_L-V_C }{ V_R } =tan^{-1} \displaystyle \frac{ X_L-X_C }{ R }$
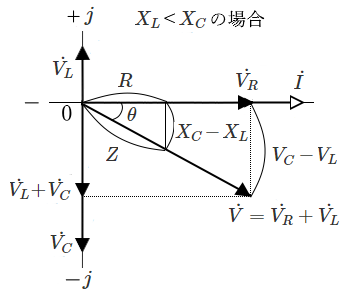
【$X_L<X_C$ の場合】
$V=\sqrt{{V_R}^2+(V_C-V_L)^2}=I\sqrt{R^2+(X_C-X_L)^2}$
$\begin{eqnarray}Z= \displaystyle \frac{ V }{ I}&=& \sqrt{R^2+(X_C-X_L)^2}\\\\&=&\displaystyle \sqrt{R^2+(\frac{ 1 }{ ωC }-ωL)^2}\end{eqnarray}$
$θ=tan^{-1} \displaystyle \frac{ V_C-V_L }{ V_R } =tan^{-1} \displaystyle \frac{ X_C-X_L }{ R }$
$X_L$[Ω]:誘導性リアクタンス
$X_C$[Ω]:容量性リアクタンス
$V_R$[V],$V_C$[V]:各電圧
$V$[V]:全電圧
$Z$[Ω]:インピーダンス
$θ$[rad]:位相差
インピーダンス三角形は、電流 $I$ を基準とした電圧のフェーザ図と相似になります。
$RLC$ 直列回路の例題
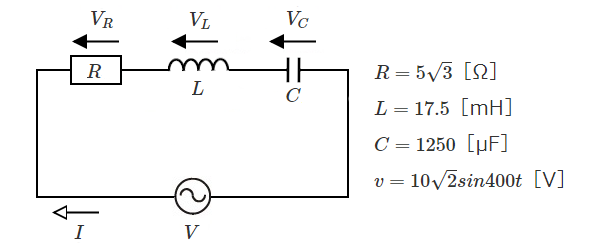
図の回路の誘導性リアクタンス $X_L$[Ω]、容量性リアクタンス $X_C$[Ω]、合成インピーダンス $Z$[Ω]、電流 $I$[A]、$R$,$L$,$C$に生じる電圧降下 $V_R$,$V_L$,$V_C$ を求めてみます。
誘導性リアクタンスと容量性リアクタンス
誘導性リアクタンス $X_L$[Ω]は、
$\begin{eqnarray}X_L&=&ωL\\\\&=&400×17.5×10^{-3}=7[Ω]\end{eqnarray}$
容量性リアクタンス $X_C$[Ω]は、
$\begin{eqnarray}X_C&=&\displaystyle \frac{ I }{ ωC }\\\\&=&\displaystyle \frac{ I }{400×1250×10^{-6} }\\\\&=&\displaystyle \frac{1 }{0.5 }=2[Ω]\end{eqnarray}$
合成インピーダンス
$RLC$ 直列回路の合成インピーダンスは、各インピーダンスのベクトル合計です。
$\begin{eqnarray}\dot{Z}&=&R+\dot{X_L}+\dot{X_C}\\\\&=&R+jX_L-jX_C\\\\&=&R+j(X_L-X_C)\\\\&=&5\sqrt{3}+j(7-2)\\\\&=&5\sqrt{3}+j5[Ω]\end{eqnarray}$
フェーザ図は次のようになります。
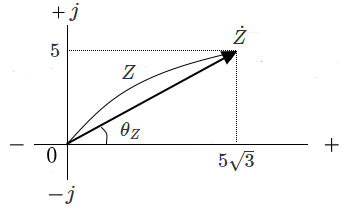
図よりインピーダンス $\dot{Z}$ の大きさと、偏角 $θ_Z$ を求めてみます。
$\begin{eqnarray}|Z|&=&\sqrt{(5\sqrt{3})^2+5^2}\\\\&=&\sqrt{75+25}=\sqrt{100}=10[Ω]\end{eqnarray}$
$\begin{eqnarray}θ_Z&=&tan^{-1}\displaystyle \frac{ 5 }{5\sqrt{3} }\\\\&=&tan^{-1}\displaystyle \frac{ 1}{\sqrt{3} }\\\\&=&\displaystyle \frac{ π }{6 }\end{eqnarray}$
電流
$RLC$ 直列回路に流れる電流のベクトル $\dot{I}$ は、電圧の実効値を $\dot{V}$ とすると、オームの法則より
$\begin{eqnarray}\dot{I}&=&\displaystyle \frac{ \dot{V} }{\dot{Z} }\\\\&=&\displaystyle \frac{ 10 }{5\sqrt{3}+j5 }\\\\&=&\displaystyle \frac{ 10(5\sqrt{3}-j5) }{(5\sqrt{3}+j5)(5\sqrt{3}-j5) }\\\\&=&\displaystyle \frac{ 50\sqrt{3}-j50 }{(5\sqrt{3})^2-(j5)^2 }\\\\&=&\displaystyle \frac{ 50\sqrt{3}-j50 }{75+25 }\\\\&=&\displaystyle \frac{ 50\sqrt{3}-j50 }{100 }\\\\&=&\displaystyle \frac{ \sqrt{3} }{2 }-j\displaystyle \frac{ 1 }{2 }\end{eqnarray}$
フェーザ図は次のようになります。
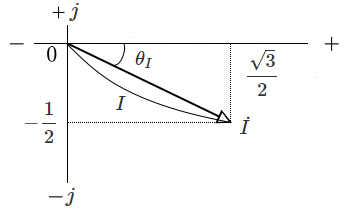
図より電流 $\dot{I}$ の大きさ(実効値)と、偏角(位相) $θ_I$ を求めてみます。
$\begin{eqnarray}I&=&\displaystyle\sqrt{\left( \frac{ \sqrt{3} }{2}\right)^2+\left( \frac{ 1 }{2}\right)^2}\\\\&=&\displaystyle\sqrt{ \frac{ 3 }{4}+ \frac{ 1 }{4}}=1[A]\end{eqnarray}$
$\begin{eqnarray}θ_I&=&tan^{-1}\displaystyle \frac{ -\displaystyle \frac{1 }{2 } }{\displaystyle \frac{ \sqrt{3} }{2 } }\\\\&=&tan^{-1}(- \frac{ 1}{\sqrt{3} })\\\\&=&-\displaystyle \frac{ π }{6 }\end{eqnarray}$
電流を瞬時値 $i$[A]で表してみると、
$i=\sqrt{2}sin(400t-\displaystyle \frac{ π }{6 })$[A]
電圧降下
$R$,$L$,$C$に生じる電圧降下 $V_R$,$V_L$,$V_C$ を求めてみます。
$\begin{eqnarray}\dot{V_R}&=&R\dot{I}\\\\&=&5\sqrt{3}\left(\displaystyle \frac{ \sqrt{3} }{2 }-j\displaystyle \frac{ 1 }{2 }\right)\\\\&=&\displaystyle \frac{ 5\sqrt{3}×\sqrt{3} }{2 }-j\displaystyle \frac{ 5\sqrt{3} }{2 }\\\\&=&\displaystyle \frac{ 15 }{2 }-j\displaystyle \frac{ 5\sqrt{3} }{2 }\end{eqnarray}$
$\begin{eqnarray}\dot{V_L}&=&jX_L\dot{I}\\\\&=&j7\left(\displaystyle \frac{ \sqrt{3} }{2 }-j\displaystyle \frac{1 }{2 }\right)\\\\&=&\displaystyle \frac{ 7 }{2 }+j\displaystyle \frac{7 \sqrt{3} }{2 }\end{eqnarray}$
$\begin{eqnarray}\dot{V_C}&=&-jX_C\dot{I}\\\\&=&-j2\left(\displaystyle \frac{ \sqrt{3} }{2 }-j\displaystyle \frac{1 }{2 }\right)\\\\&=&-1-j\sqrt{3} \end{eqnarray}$
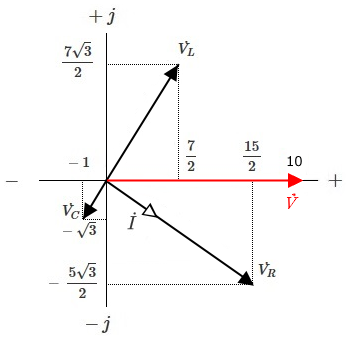
キルヒホッフの法則は、交流回路においても成り立ちます。キルヒホッフの電圧測が成り立つのかを試してみます。電源電圧の実効値 $\dot{V}$ は、$\dot{V}=\dot{V_R}+\dot{V_L}+\dot{V_C}$ ですので、
$\begin{eqnarray}\dot{V}&=&\dot{V_R}+\dot{V_L}+\dot{V_C}\\\\&=&(\displaystyle \frac{ 15 }{2 }-j\displaystyle \frac{ 5\sqrt{3} }{2 })+(\displaystyle \frac{ 7 }{2 }+j\displaystyle \frac{7 \sqrt{3} }{2 })+(-1-j\sqrt{3} )\\\\&=&(\displaystyle \frac{ 15 }{2 }+\displaystyle \frac{ 7 }{2 }-1)+j(-\displaystyle \frac{ 5\sqrt{3} }{2 }+\displaystyle \frac{7 \sqrt{3} }{2 }-\sqrt{3})\\\\&=&10+j0\end{eqnarray}$
電験三種-理論の過去問解説:単相交流の直列回路
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1998年(平成10年)問7【電験理論の過去問題】
図のような交流回路において、抵抗 $R$ の両端の電圧 $V_R$[V]の値が電源電圧 $V$[V]の値の $\displaystyle \frac{ 1 }{\sqrt{2}}$ 倍であった。このときの抵抗 $R$[Ω]とインダクタンス $L$[H]との関係を表す式として、正しいのは次のうちどれか。ただし、電源電圧の各周波数は $ω$[rad/s]とする。
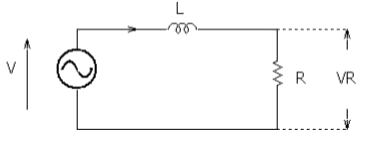
(1) $R=L$ (2) $L=ωR$ (3) $ωLR=1$ (4) $R=ωL$ (5) $ω=LR$
誘導性リアクタンスを $X_L=ωL$[Ω]とすると回路の合成インピーダンス $Z$[Ω]は、
$Z=\sqrt{R^2+{X_L}^2}$[Ω]
分圧の法則より
$\begin{eqnarray}V_R&=&\displaystyle \frac{ R }{Z}×V\\\\&=&\displaystyle \frac{ R }{\sqrt{R^2+{X_L}^2}}×V=\displaystyle \frac{ 1 }{\sqrt{2}}V\end{eqnarray}$
$\sqrt{2}R=\sqrt{R^2+{X_L}^2}$
$2R^2=R^2+{X_L}^2$
$R=X_L=ωL$
答え (4)
2000年(平成12年)問9【電験理論の過去問題】
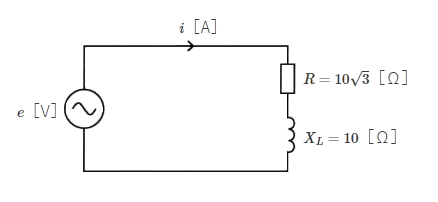
図のような回路において、電源電圧が $e=200sin(ωt+\displaystyle \frac{ π }{4})$[V]であるとき、回路に流れる電流 $i$[A]を表す式として正しいのは次のうちどれか。
(1) $i=10sin(ωt+\displaystyle \frac{ π }{12})$
(2) $i=5\sqrt{2}sin(ωt-\displaystyle \frac{ π }{6})$
(3) $i=10\sqrt{2}sin(ωt+\displaystyle \frac{ π }{6})$
(4) $i=5\sqrt{2}sin(ωt-\displaystyle \frac{ π }{12})$
(5) $i=10sin(ωt-\displaystyle \frac{ π }{12})$
回路の合成インピーダンス $Z$[Ω]は
$Z=\sqrt{R^2+X_L^2}=\sqrt{(10\sqrt{3})^2+10^2}=20$[Ω]
電流の実効値を $I$[A]とすると、
$I=\displaystyle \frac{ V }{Z}=\displaystyle \frac{\frac{200 }{\sqrt{2}} }{20}=\displaystyle \frac{10 }{\sqrt{2}}$
電源電圧 $e$[V]と電流 $I$[A]の位相差を $ θ$ とすると、
$\begin{eqnarray}θ&=& tan^{-1}\displaystyle \frac{ X_L }{ R } \\\\&=& tan^{-1}\displaystyle \frac{10}{ 10\sqrt{3} }\\\\&=& tan^{-1}\displaystyle \frac{1}{ \sqrt{3} } = \displaystyle \frac{π}{ 6 } \end{eqnarray}$
合成負荷は誘導性なので、電流の瞬時値 $i$[A]は電源電圧 $e$[V]より、$ \displaystyle \frac{π}{ 6 } $ 遅れます。したがって、
$\begin{eqnarray}i&=&\displaystyle \frac{10 }{\sqrt{2}}×\sqrt{2}sin(ωt+\displaystyle \frac{ π }{4}-\displaystyle \frac{π}{ 6 })\\\\&=&10sin(ωt+\displaystyle \frac{ π }{12})[A]\end{eqnarray}$
答え (1)
2003年(平成15年)問16【電験理論の過去問題】
図1のように、抵抗 $R_0=16$[Ω]、インピーダンス $\dot{Z}$[Ω]の誘導性負荷(抵抗 $R$[Ω]、誘導性リアクタンス $X$[Ω])を直列に接続した交流回路がある。 正弦波交流電圧 $\dot{E}=10\sqrt{3}$[V]の電源をこの回路に接続したところ、$R_0$ の端子間電圧の大きさ、誘導性負荷の端子間電圧の大きさは、それぞれ $10$[V]であった。 次の(a)及び(b)に答よ。
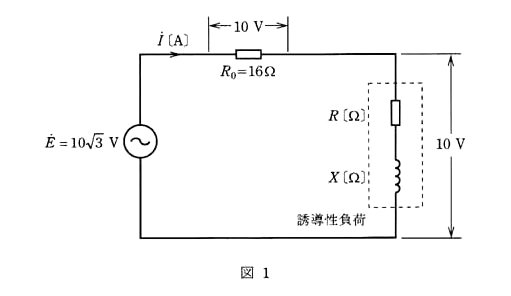
(a) 回路に流れる電流を $\dot{I}$[A]とすれば、$\dot{E}$、$R_0\dot{I}$、$\dot{Z}\dot{I}$ の関係をベクトル図で表すと図2のようになる。電流 $\dot{I}$[A]の大きさの値と、電圧 $\dot{E}$ と電流 $\dot{I}$ の位相差 $θ$[°]の値として、正しいものを組み合わせたものは次のうちどれか。
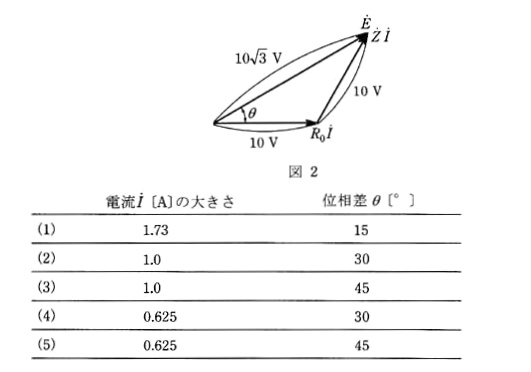
(b) $\dot{E}$、$(R_0+R)\dot{I}$、$X\dot{I}$ の関係をベクトル図で表すと図3のようになる。これより、$R$[Ω]と $X$[Ω]の値として、最も近いものを組み合わせたものは次のうちどれか。
(a) 抵抗 $R_0$ の電圧降下は $10$[V]ですので、
$I=\displaystyle \frac{10}{R_0}=\displaystyle \frac{10}{16}=0.625$[A]
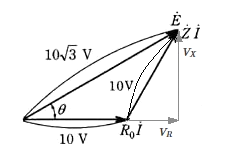
抵抗 $R$ による電圧降下を $R_L$[Ω]、誘導性リアクタンス $X$ による 電圧降下を $V_X$[Ω]とすると、
$10^2={V_R}^2+{V_X}^2$ … (1)
$(10\sqrt{3})^2=(10+V_R)^2+{V_X}^2$
$300=100+20V_R+{V_R}^2+{V_X}^2$
$200=20V_R+{V_R}^2+{V_X}^2$ … (2)
(1),(2)式より
$200=20V_R+100$
$V_R=5$[V]
$\begin{eqnarray}θ&=&cos^{-1}\left(\displaystyle \frac{R_0I+V_R}{E}\right)\\\\&=&cos^{-1}\left(\displaystyle \frac{10+5}{10\sqrt{3}}\right)\\\\&=&cos^{-1}\left(\displaystyle \frac{3}{2\sqrt{3}}\right)\\\\&=&cos^{-1}\left(\displaystyle \frac{\sqrt{3}}{2}\right)=\displaystyle \frac{π}{6}\end{eqnarray}$
答え (4)
(b) $R$[Ω]と $X$[Ω]の値は、
$R=\displaystyle \frac{V_R}{I}=\displaystyle \frac{5}{0.625}=8$[Ω]
(1)式より
$10^2=5^2+{V_X}^2$
${V_X}^2=75$
$V_X=5\sqrt{3}$ [Ω]
$X=\displaystyle \frac{V_L}{I}=\displaystyle \frac{5\sqrt{3}}{0.625}=13.9$[Ω]
答え (2)
2004年(平成16年)問8【電験理論の過去問題】
図1のような抵抗 $R$[Ω]と誘導性リアクタンス $X$[Ω]との直列回路がある。この回路に正弦波交流電圧 $E=100$[V]を加えたとき、回路に流れる電流は $10$[A]であった。この回路に図2のように、更に抵抗 $11$[Ω]を直列接続したところ、回路に流れる電流は $5$[A]になった。抵抗 $R$[Ω]の値として、最も近いのは次のうちどれか。
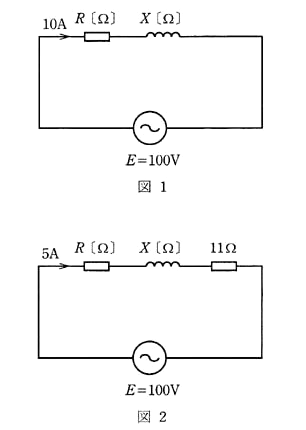
(1) 5.5 (2) 8.1 (3) 8.6 (4) 11.4 (5) 16.7
図1の回路の合成インピーダンスを $Z_1$[Ω]とすると、
$Z_1=\displaystyle \frac{100}{10}=10$[Ω]
${Z_1}^2=R^2+X^2$
$R^2+X^2=100$ … (1)
図2の回路の合成インピーダンスを $Z_2$[Ω]とすると、
$Z_2=\displaystyle \frac{100}{5}=20$[Ω]
${Z_2}^2=(R+11)^2+X^2$
$R^2+22R+X^2=279$ … (2)
(1),(2)式より、
$22R+100=279$
$22R=179$
$R=\displaystyle \frac{179}{22}≒8.14$[Ω]
答え (2)
2006年(平成18年)問9【電験理論の過去問題】
図のように、$R$[Ω]の抵抗インダクタンス $L$[H]のコイルを直列に接続した回路がある。この回路に角周波数 $ω$[rad/s]の正弦波交流電圧 $\dot{E}$[V]を加えたとき、この電圧の位相[rad]に対して回路を流れる電流 $\dot{I}$[A]の位相[rad]として、正しいのは次のうちどれか。
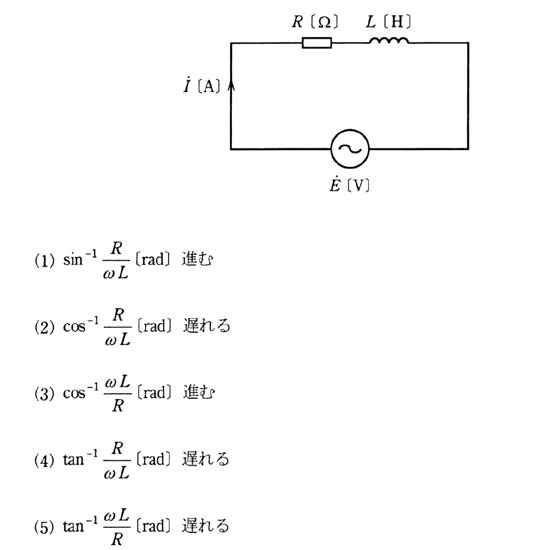
抵抗 $R$ の電圧降下を $V_R$、インダクタンス $L$ の電圧降下を $V_L$ とすると、
$\dot{V_R}=R\dot{I}$
$\dot{V_L}=jωL\dot{I}$
電源電圧 $\dot{E}$ と電流 $\dot{I}$ の位相差 $θ$ は、
$θ=tan^{-1} \displaystyle \frac{ V_L }{ V_R } =tan^{-1} \displaystyle \frac{ ωL }{ R } $
合成負荷は誘導性なので、電流は電源電圧 より、$ tan^{-1} \displaystyle \frac{ ωL }{ R } $ 遅れます。
答え (5)
2009年(平成21年)問8【電験理論の過去問題】
図のように、$R=\sqrt{3}ωL$[Ω]の抵抗、インダクタンス $L$[H]のコイル、スイッチ S が角周波数 $ω$[rad/s]の交流電圧 $\dot{E}$[V]の電源に接続されている。スイッチ S を開いているとき、コイルを流れる電流の大きさを $I_1$[A]、電源電圧に対する電流の位相差を $θ_1$[°]とする。また、スイッチ S を閉じているとき、コイルを流れる電流の大きさを $I_2$[A]、電源電圧に対する電流の位相差を $θ_2$[°]とする。このとき、$\displaystyle\frac{I_1}{I_2}$ 及び $|θ_1-θ_2|$[°]の値として、正しいものを組み合わせたのは次のうちどれか。
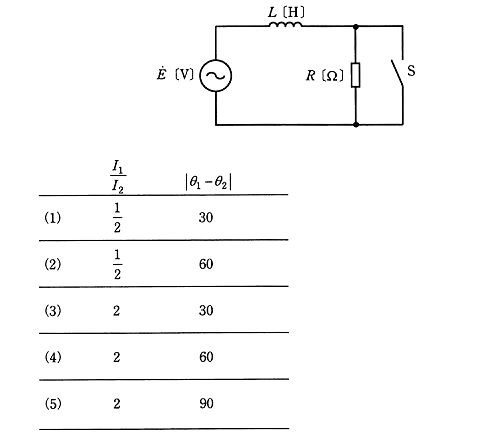
スイッチ S を開いているとき、電流の大きさと $I_1$[A]と電源電圧 $\dot{E}$ ,電流 $\dot{I_1}$ 間の位相差 $θ_1$ は、
$\begin{eqnarray}I_1&=& \displaystyle \frac{ E }{ \sqrt{R^2+(ωL)^2}}\\\\&=& \displaystyle \frac{ E }{ \sqrt{(\sqrt{3}ωL)^2+(ωL)^2}}\\\\&=& \displaystyle \frac{ E }{ \sqrt{R^2+(ωL)^2}}= \displaystyle \frac{ E }{ 2ωL}\end{eqnarray}$
$\begin{eqnarray}θ_1&=& tan^{-1}\displaystyle (\frac{ ωL }{ R }) \\\\&=& tan^{-1}\displaystyle( \frac{ ωL }{ \sqrt{3}ωL } )\\\\&=&tan^{-1}\displaystyle( \frac{ 1 }{ \sqrt{3} } )=30[°]\end{eqnarray}$
スイッチ S が閉じているとき、電流の大きさと $I_2$[A]と電源電圧 $\dot{E}$ ,電流 $\dot{I_2}$ 間の位相差 $θ_2$ は、
$I_2= \displaystyle \frac{ E }{ ωL}$
$θ_2= tan^{-1}\displaystyle (\frac{ ωL }{ 0 }) = tan^{-1}∞=90[°]$
したがって、$\displaystyle\frac{I_1}{I_2}$ 及び $|θ_1-θ_2|$[°]のは、
$\displaystyle\frac{I_1}{I_2}=\displaystyle\frac{\displaystyle \frac{ E }{ 2ωL}}{\displaystyle \frac{ E }{ ωL}}=\displaystyle\frac{1}{2}$
$|θ_1-θ_2|=|30-90|=60$[°]
答え (2)
2011年(平成23年)問9【電験理論の過去問題】
図のように、$1000$[Ω]の抵抗と静電容量 $C$[μF]のコンデンサを直列に接続した交流回路がある。いま、電源の周波数が $1000$[Hz]のとき,電源電圧 $\dot{E}$[V]と電流 $\dot{I}$[A]の位相差は $\displaystyle\frac{π}{3}$[rad]であった。このとき、コンデンサの静電容量 $C$[μF]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
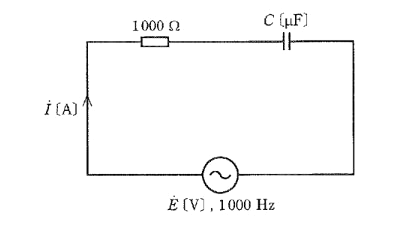
(1) 0.053 (2) 0.092 (3) 0.107 (4) 0.159 (5) 0.258
インピーダンス角 $θ$ は、電源電圧 $\dot{E}$[V]と電流 $\dot{I}$[A]の位相差に等しくなりますので、
$tan\displaystyle\frac{π}{3}=\displaystyle \frac{ X_C }{ R}$
$X_C=Rtan\displaystyle\frac{π}{3}=1000\sqrt{3}$[Ω]
容量性リアクタンス $X_C$[Ω]は、
$X_C=\displaystyle \frac{ 1 }{ ωC×10^{-6} }=\displaystyle \frac{ 1 }{ 2πfC ×10^{-6}}$
$1000\sqrt{3}=\displaystyle \frac{ 1 }{ 2π×1000×C ×10^{-6}}$
これを計算すると、
$C=0.092$[μF]
答え (2)
2013年(平成25年)問7【電験理論の過去問題】
$4$[Ω]の抵抗と静電容量が $C$[F]のコンデンサを直列に接続したRC回路がある。このRC回路に、周波数 $50$[Hz]の交流電圧 $100$[V]の電源を接続したところ、$20$[A]の電流が流れた。では、このRC回路に、周波数 $60$[Hz]の交流電圧 $100$[V]の電源を接続したとき、RC回路に流れる電流[A]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 16.7 (2) 18.6 (3) 21.2 (4) 24.0 (5) 25.6
周波数 $50$[Hz]の電源を接続したときのコンデンサのリアクタンスを $X_{50}$ とすると、
$I_{50}=\displaystyle \frac{ 100 }{ \sqrt{4^2+{X_{50}}^2 }}=20$
$16+{X_{50}}^2=25$
$X_{50}=3$[Ω]
$X_C=\displaystyle \frac{ 1}{ 2πfC }$ なので、
$X_{50}=\displaystyle \frac{ 1}{ 2π×50×C }=3$
$C=\displaystyle \frac{ 1}{ 300π }$
周波数 $60$[Hz]の電源を接続したときのコンデンサのリアクタンスを $X_{60}$ とすると、
$X_{60}=\displaystyle \frac{ 1}{ 2π×60×\displaystyle \frac{ 1}{ 300π } }=2.5$ [Ω]
周波数 $60$[Hz]の電源を接続したときに流れる電流 $I_{60}$[A]は、
$I_{60}=\displaystyle \frac{ 100 }{ \sqrt{4^2+{2.5}^2 }}≒21.2$
答え (3)
2017年(平成29年)問8【電験理論の過去問題】
図のように、交流電圧 $E=100V$ の電源、誘導性リアクタンス $X=4Ω$ のコイル、$R_1$[Ω],$R_2$[Ω]の抵抗からなる回路がある。いま、回路を流れる電流の値が $I=20A$ であり、また、抵抗 $R_1$ に流れる電流 $I_1$[A]と抵抗 $R_2$ に流れる電流 $I_2$[A]との比が、$I_1:I_2 = 1:3$ であった。このとき、抵抗 $R_1$ の値[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
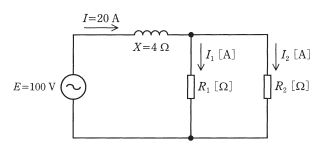
(1) 1.0 (2) 3.0 (3) 4.0 (4) 9.0 (5) 12
抵抗 $R_1$ , $R_2$ にかかる電圧は等しく、この電圧を $V_R$[V]、誘導性リアクタンス $X$ にかかる電圧を $V_X$[V]とすると、電流 $I$[A]を基準としたフェーザ図は次のようになります。
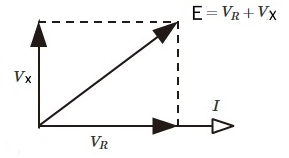
フェーザ図より、
$E^2=V_R^2+{V_X}^2=V_R^2+(XI)^2$
$100^2=V_R^2+(4×20)^2$
${V_R}^2=10000-6400=3600$
$V_R=60$[V]
問題文に $I_1:I_2 = 1:3$ とありますので、
$I_2 = 3I_1$
電流 $I=I_1+I_2=20$[A]ですので、
$I=I_1+I_2=I_1+3I_I=4I_I=20$[A]
$I_I=5$[A]
したがって、抵抗 $R_1$[Ω]の値は、
$R_1=\displaystyle\frac{V_R}{I_1}=\displaystyle\frac{60}{5}=12$[Ω]
答え(5)
2018年(平成30年)問8【電験理論の過去問題】
図のように、角周波数の $ω$ [rad/s]の交流電源と力率 $\displaystyle\frac{1}{\sqrt{2}}$ の誘導性負荷 $\dot{Z}$ [Ω]との間に、抵抗値 $R$ [Ω]の 抵抗器とインダクタンス $L$ [H]のコイルが接続されている。$R=ωL$ とするとき、電源電圧 $\dot{V_1}$ [V]と負荷の端子電圧 $\dot{V_2}$ [V]との位相差の値[°]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
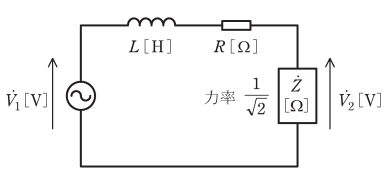
(1) 0 (2) 30 (3) 45 (4) 60 (5) 90
誘導性負荷 $\dot{Z}$ のインピーダンスベクトルを図示します。力率が $\displaystyle\frac{1}{\sqrt{2}}$ ですので、インピーダンス角は45°になります。
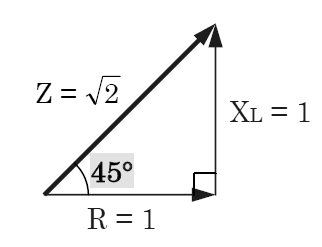
$R$ と $L$ の合成インピーダンスベクトルを図示します。問題中に、「$R=ωL$ とするとき」と記述がありますので、$R=X_L$ であることを表しています。つまり、上のインピーダンス三角形と同じ形になります。
RとLの合成インピーダンス + $\dot{Z}$ のベクトル角は、どちらもベクトル角が 45°ですので、足し合わせても 45°になります。
問題は「RとLの合成にかかる電圧 + 誘導性負荷 Z にかかる電圧」と「誘導性負荷 Z にかかる電圧」との位相差を求めよという問題ですので、「RとLの合成にかかる電圧 + 誘導性負荷 Z にかかる電圧」と「誘導性負荷 Z にかかる電圧」ともに、ベクトル角が 45°となり、位相差は 0 になります。
答え(1)
電験三種の理論科目に出題される「単相交流分野」のページ
1.正弦波交流の波形
2.単相交流の直列回路
3.単相交流の並列回路
4.RLC直列共振回路
5.RLC並列共振回路
6.単相交流の電力と力率
電験三種の理論科目に出題される「三相交流分野」のページ
1.三相交流回路
2.三相交流の電力と力率






