第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される三相交流の電力と力率について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された三相交流の電力と力率の過去問題も解説しています。
- 三相交流の電力
- 三相交流の力率
- 電験三種-理論の過去問解説:三相交流の電力と力率
- 1997年(平成9年)問11【電験理論の過去問題】
- 1999年(平成11年)問9【電験理論の過去問題】
- 2004年(平成16年)問16【電験理論の過去問題】
- 2005年(平成17年)問7【電験理論の過去問題】
- 2006年(平成18年)問15【電験理論の過去問題】
- 2007年(平成19年)問15【電験理論の過去問題】
- 2008年(平成20年)問15【電験理論の過去問題】
- 2010年(平成22年)問9【電験理論の過去問題】
- 2010年(平成22年)問15【電験理論の過去問題】
- 2011年(平成23年)問15【電験理論の過去問題】
- 2013年(平成25年)問15【電験理論の過去問題】
- 2014年(平成26年)問14【電験理論の過去問題】
- 2014年(平成26年)問16【電験理論の過去問題】
- 2015年(平成27年)問17【電験理論の過去問題】
- 2017年(平成29年)問16【電験理論の過去問題】
三相交流の電力
三相交流の電力は、3つの相の電力を加えることによって導き出すことができます。特に、平衡三相回路では、「一相の電力の3倍]になります。
いま、相電圧を $V_p$[V]、相電流を $I_p$[A]、相電圧と相電流の位相差を $θ$[rad]としたとき、一相分の電力は $V_pI_pcosθ$ ですので、三相電力 $P$[W]は次のようになります。
$P=3V_pI_pcosθ$[W]
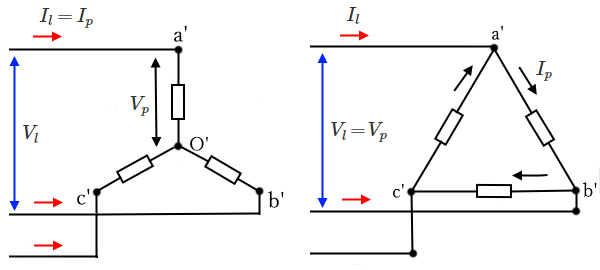
$P=3V_pI_pcosθ$[W]は、相電圧と相電流で表しています。一般的には、三相の電流や電圧を表す場合、線間電圧と線電流を用います。
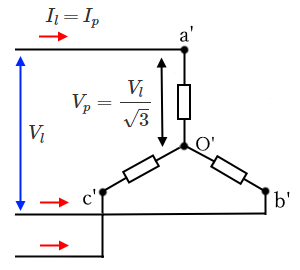
Y結線負荷の場合は、相電圧 $V_p=\displaystyle\frac{V_l}{\sqrt{3}}$[V]、相電流 $I_p=I_l$ ですので、三相電力 $P$[W]は、
$P=3×\displaystyle\frac{V_l}{\sqrt{3}}×I_l×cosθ=\sqrt{3}V_lI_lcosθ$[W]
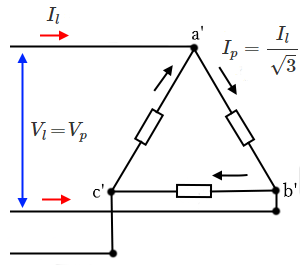
Δ結線負荷の場合は、相電圧 $V_p=V_l$[V]、相電流 $I_p=\displaystyle\frac{I_l}{\sqrt{3}}$ ですので、三相電力 $P$[W]は、
$P=3V_l×\displaystyle\frac{I_l}{\sqrt{3}}×cosθ=\sqrt{3}V_lI_lcosθ$[W]
つまり、三相電力は負荷の結線に関係がなく、次のように表すことができます。
$三相電力=\sqrt{3}×線間電圧×線電流×力率$
相電圧 $V_p$ , 相電流 $I_p$ を使った三相電力 $P$ を求める公式
$P=3V_pI_pcosθ$[W]
$P$[W]:電力
$V_p$[V]:相電圧
$I_p$[A]:相電流
$cosθ$:力率
線間電圧 $V_l$ 線電流 $I_l$ を使った三相電力 $P$ を求める公式
$P=\sqrt{3}V_lI_lcosθ$[W]
$P$[W]:電力
$V_l$[V]:線間電圧
$I_l$[A]:線電流
$cosθ$:力率
三相交流の力率
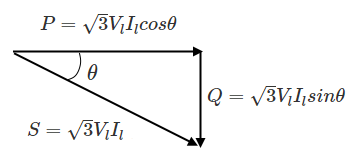
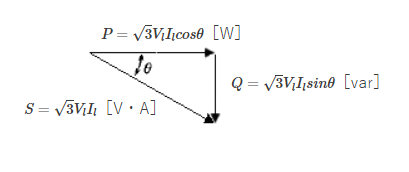
三相電力は、単相電力と同じように、皮相電力 $S$[VA]、有効電力 $P$[W]、無効電力 $Q$[var]で表すことができます。
皮相電力、有効電力、無効電力の公式
皮相電力:$S=\sqrt{3}V_lI_l$[VA]
有効電力:$P=\sqrt{3}V_lI_lcosθ$[W]
無効電力:$Q=\sqrt{3}V_lI_lsinθ$[var]
$S=\sqrt{P^2+Q^2}$
電験三種-理論の過去問解説:三相交流の電力と力率
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1997年(平成9年)問11【電験理論の過去問題】
図のような平衡三相回路において、負荷の力率の値として、正しいのは次のうちどれか。ただし、電源の角周波数をω[rad/s]とする。
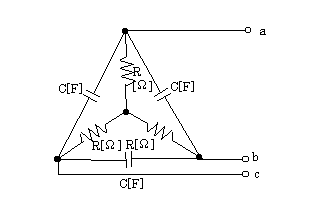
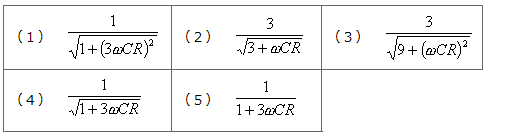
静電容量 $C$[F]のコンデンサをΔ→Y変換すると、$3C$[F]となります。相電圧を $\dot{E}$[V]とし、Y接続した一相分について、各素子に流れる電流をベクトル図で表示します。
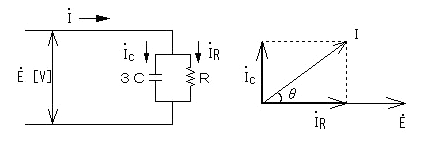
図より、負荷の力率 $cosθ$ は、
$\begin{eqnarray}cosθ=\displaystyle\frac{I_R}{I}&=&\displaystyle\frac{I_R}{\sqrt{I_R^2+I_C^2}}\\\\&=&\displaystyle\frac{\displaystyle\frac{E}{R}}{\sqrt{(\displaystyle\frac{E}{R})^2+(3ωCE)^2}}\\\\&=&\displaystyle\frac{\displaystyle\frac{1}{R}}{\sqrt{(\displaystyle\frac{1}{R})^2+(3ωCR)^2}}\\\\&=&\displaystyle\frac{1}{\sqrt{(1+(3ωC)^2}}\end{eqnarray}$
答え (1)
1999年(平成11年)問9【電験理論の過去問題】
図のような平衡三相回路において、負荷の全消費電力[kW]の値として、正しいのは次のうちどれか。
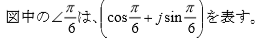
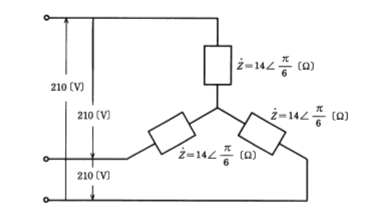
(1) 1.58 (2) 1.65 (3) 2.73 (4) 2.86 (5) 4.73
線電流を $I_l$[A]とすると、
$I_l=\displaystyle\frac{\displaystyle\frac{V}{\sqrt{3}}}{Z}=\displaystyle\frac{\displaystyle\frac{210}{\sqrt{3}}}{14}=\displaystyle\frac{15}{\sqrt{3}}$[A]
$cosθ=\displaystyle\frac{\sqrt{3}}{2}$ ですので、全消費電力 $P$[kW]は、
$\begin{eqnarray}P&=&\sqrt{3}V_lI_lcosθ\\\\&=&\sqrt{3}×210×\displaystyle\frac{15}{\sqrt{3}}×\displaystyle\frac{\sqrt{3}}{2}\\\\&=&2.73[kW]\end{eqnarray}$
答え (3)
2004年(平成16年)問16【電験理論の過去問題】
図1のように、相電圧 200[V]、周波数 50[Hz]の対称三相交流電源に、抵抗とインダクタンスからなる三相平衡負荷を接続した交流回路がある。次の(a)及び(b)に答よ。
(a) 図1の回路において、負荷電流 $I$[A]の値として、最も近いものは次のうちどれか。
(1) 69.2 (2) 66.6 (3) 40 (4) 23.1 (5) 22.2
(b) 図2のように、静電容量 $C$[F]のコンデンサをΔ結線して、その端子 a’、b’ 及び c’ をそれぞれ図1の端子 a、b 及び c に接続した。その結果、三相交流電源から見た負荷の力率は 1 になった。静電容量 $C$[F]の値として、最も近いものは次のうちどれか。
(1) $5.9×10^{-2}$ (2) $7.4×10^{-4}$ (3) $2.1×10^{-4}$ (4) $1.7×10^{-4}$ (5)$1.9×10^{-6}$
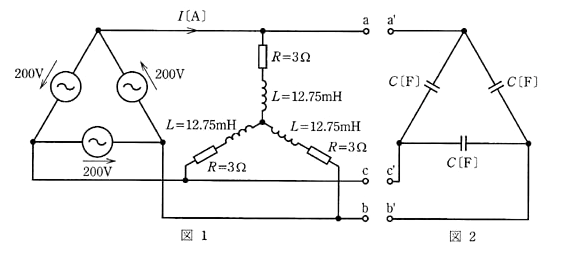
(a) Y回路の相電圧を $V_p$[V]、誘導性リアクタンスを $X_L$[Ω]、相電流を $I_P$[A]とすると、
$V_p=\displaystyle\frac{200}{\sqrt{3}}$[V]
$X_L=2πfL=2π×50×12.75×10^{-3}=4$[Ω]
$I_P=\displaystyle\frac{V_p}{Z}=\displaystyle\frac{\displaystyle\frac{200}{\sqrt{3}}}{\sqrt{3^2+4^2}}=23.1$[A]
答え (4)
(b) 無効力率は、
$sinθ=\displaystyle\frac{X_L}{Z}=\displaystyle\frac{4}{5}=0.8$
ですので、遅れ無効電流を $I_Q$[A]とすると、
$I_Q=23.1×0.8=18.5$[A]
この遅れ無効電流を改善するために、コンデンサ回路から進み無効電流が流れます。コンデンサ回路の線電流を $I_C$[A]、コンデンサの容量性リアクタンスを $X_C$[Ω]とすると、
$I_C=\displaystyle\frac{18.5}{\sqrt{3}}$[A]
$X_C=\displaystyle\frac{V_p}{I_C}=\displaystyle\frac{200}{\displaystyle\frac{18.5}{\sqrt{3}}}=18.7$[Ω]
$X_C=\displaystyle\frac{1}{ωC}=\displaystyle\frac{1}{2πfC}$[Ω]ですので、
$\displaystyle\frac{1}{2πfC}=18.7$[Ω]
$C=1.7×10^{-4}$[F]
答え (4)
2005年(平成17年)問7【電験理論の過去問題】
図のように、相電圧 10[kV]の対称三相交流電源に、抵抗 $R$[Ω]と誘導性リアクタンス $X$[Ω]からなる平衡三相負荷を接続した回路がある。
平衡三相負荷の全消費電力が 200[kW]、線電流 $\dot{I}$[A]の大きさ(スカラ量)が 20[A]のとき、$R$[Ω]と $X$[Ω]の値として、正しいものを組み合わせたのは次のうちどれか。
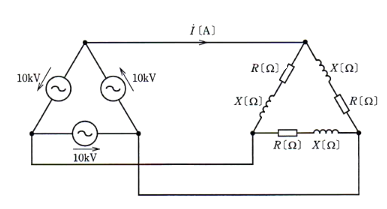

Δ結線は、相電圧=線間電圧ですので、力率 $cosθ$ は、
$P=\sqrt{3}V_lI_lcosθ$[W]
$200=\sqrt{3}×10×20×cosθ$
$cosθ=\displaystyle\frac{1}{\sqrt{3}}$
線電流の大きさを $I_l$[A]、相電流の大きさを $I_p$[A]とすると、
$I_p=\displaystyle\frac{I_l}{\sqrt{3}}=\displaystyle\frac{20}{\sqrt{3}}$[A]
負荷のインピーダンス $Z$[Ω]より、抵抗 $R$[Ω]と誘導性リアクタンス $X$[Ω]を導きます。
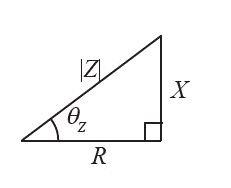
$Z=\displaystyle\frac{V_p}{I_p}=\displaystyle\frac{10×10^3}{\displaystyle\frac{20}{\sqrt{3}}}=\displaystyle\frac{\sqrt{3}}{2}×10^3$[Ω]
$R=Zcosθ=\displaystyle\frac{\sqrt{3}}{2}×10^3×\displaystyle\frac{1}{\sqrt{3}}=500$[Ω]
$X=Zsinθ=\displaystyle\frac{\sqrt{3}}{2}×10^3×\displaystyle\frac{\sqrt{2}}{\sqrt{3}}=500\sqrt{2}$[Ω]
答え (4)
2006年(平成18年)問15【電験理論の過去問題】
抵抗 $R$[Ω]、誘導性リアクタンス $X$[Ω]からなる平衡三相負荷(力率80[%])に対称三相交流電源を接続した交流回路がある。次の(a)及び(b)に答えよ。
(a) 図1のように、Y結線した平衡三相負荷に線間電圧 210[V]の三相電圧を加えたとき、回路を流れる線電流 $I$ は $\displaystyle\frac{14}{\sqrt{3}}$[A]であった。負荷の誘導性リアクタンス $X$[Ω]の値として、正しいのは次のうちどれか。
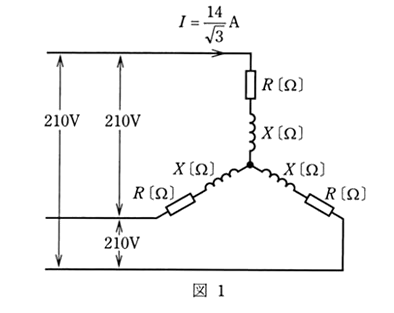
(1) 4 (2) 5 (3) 9 (4) 12 (5) 15
(b) 図1の各相の負荷を使ってΔ結線し、図2のように相電圧 200[V]の対称三相電源に接続した。この平衡三相負荷の全消費電力[kW]の値として、正しいのは次のうちどれか。
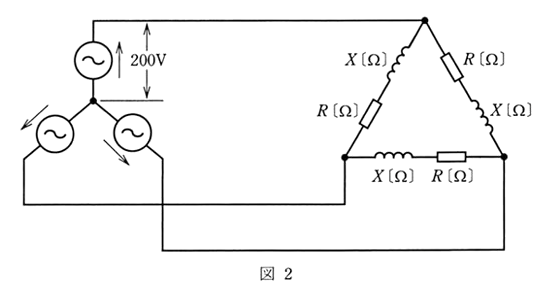
(1) 8 (2) 11.1 (3) 13.9 (4) 19.2 (5) 33.3
(a) 相電圧を $V_p$[V]とすると、 $V_p=\displaystyle\frac{210}{\sqrt{3}}$[V]ですので、1相当たりのインピーダンス $Z$[Ω]は、
$Z=\displaystyle\frac{V_p}{I}=\displaystyle\frac{\displaystyle\frac{210}{\sqrt{3}}}{\displaystyle\frac{14}{\sqrt{3}}}=15[Ω]$
負荷の誘導性リアクタンス $X$[Ω]は、
$X=Zsinθ=15×0.6=9$[Ω]
答え (3)
(b) 電源側を、Δ⇒Yに変換すると、$E_Δ=\sqrt{3}E_Y=200\sqrt{3}$[V]です。$E_Δ$[V]は、相電圧となりますので、これを $V_p$[V]とすると、一相分の電力 $p$[W]は、
$\begin{eqnarray}p&=&V_pI_pcosθ\\\\&=&\displaystyle\frac{{V_p}^2}{Z}cosθ\\\\&=&\displaystyle\frac{{(200\sqrt{3})}^2}{15}×0.8\\\\&=&6.4×10^3[W]\end{eqnarray}$
したがって、三相の電力 $P$[W]は、
$P=3p=3×6.4×10^3=19.2×10^3$[W]
答え (4)
2007年(平成19年)問15【電験理論の過去問題】
平衡三相回路について、次の(a)及び(b)に答えよ。
(a) 図1のように、抵抗 $R$ とコイル $L$ からなる平衡三相負荷に、線間電圧 200[V]、周波数 50[Hz]の対称三相交流電源を接続したところ、三相負荷全体の有効電力は $P=2.4$[kW]で、無効電力は $Q=3.2$[kvar]であった。
負荷電流 $I$[A]の値として最も近いのは次のうちどれか。
(1) 2.3 (2) 4.0 (3) 6.9 (4) 9.2 (5) 11.5
(b) 図1に示す回路の各線間に同じ静電容量のコンデンサ $C$ を図2に示すように接続した。このとき、三相電源からみた力率が1となった。このコンデンサ $C$ の静電容量[μF]の値として、最も近いのは次のうちどれか。
(1) 48.8 (2) 63.4 (3) 84.6 (4) 105.7 (5) 146.5
(a) 電力のベクトル図を示します。
上記3式の関係は次のように表すことができますので、
$S=\sqrt{P^2+Q^2}=\sqrt{2.4^2+3.2^2}=4.0$[kVA]
したがって、
$S=\sqrt{3}V_lI_l$
$4.0×10^3=\sqrt{3}×200×I_l$
$I_l=11.5$[A]
答え (5)
(b) コンデンサの容量は3個で $3ωCV^2$[var]です。これが、無効電力 $Q=3.2$[kvar]に等しいときに力率が1になりますので、
$3ωCV^2=3.2×10^3$
$3×2×π×50×C×200^2=3.2×10^3$
$C=84.6×10^{-6}$[F]
答え (3)
2008年(平成20年)問15【電験理論の過去問題】
図のように、抵抗 6[Ω]と誘導性リアクタンス 8[Ω]をY結線し、抵抗 $r$[Ω]をΔ結線した平衡三相負荷に、200[V]の対称三相交流電源を接続した回路がある。抵抗 6[Ω]と誘導性リアクタンス 8[Ω]に流れる電流の大きさを $I_1$[A]、抵抗 $r$[Ω]に流れる電流の大きさを $I_2$[A]とするとき、次の(a)及び(b)に答えよ。
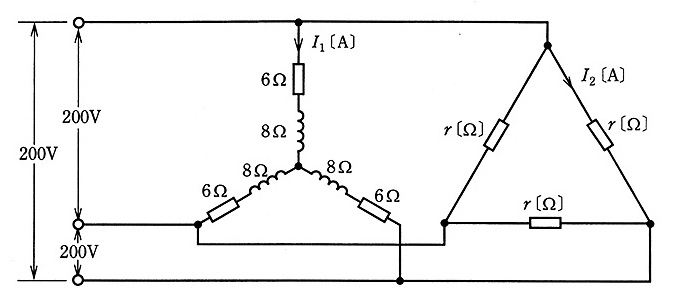
(a) 電流 $I_1$[A]と電流 $I_2$[A]の大きさが等しいとき、抵抗 $r$[Ω]の値として、最も近いのは次のうちどれか。
(1) 6.0 (2) 10.0 (3) 11.5 (4) 17.3 (5) 19.2
(b) 電流 $I_1$[A]と電流 $I_2$[A]の大きさが等しいとき、平衡三相負荷が消費する電力[kW]の値として最も近いのは次のうちどれか。
(1) 2.4 (2) 3.1 (3) 4.0 (4) 9.3 (5) 10.9
(a) 電流 $I_1$[A],$I_2$[A]は、
$I_1=\displaystyle\frac{\displaystyle\frac{200}{\sqrt{3}}}{\sqrt{6^2+8^2}}=\displaystyle\frac{20}{\sqrt{3}}$[A]
$I_2=\displaystyle\frac{200}{r}$[A]
題意より
$I_1=I_2$[A]
$\displaystyle\frac{20}{\sqrt{3}}=\displaystyle\frac{200}{r}$
$r=17.3$[Ω]
答え (4)
(b) Y部分とΔ部分の電力を分けて考えます。どちらも電力は $P=3V_pI_pcosθ$[W]で求まることができます。
まず、Y結線負荷の部分は、相電圧 $V_p=\displaystyle\frac{200}{\sqrt{3}}$[V]、相電流 $I_p=I_1$ です。インピーダンスは $Z=\sqrt{6^2+8^2}=10$[Ω]なので、力率は $cosθ=0.6$ となります。三相電力 $P_Y$[W]は、
$\begin{eqnarray}P_Y&=&3V_pI_pcosθ\\\\&=&3×\displaystyle\frac{200}{\sqrt{3}}×\displaystyle\frac{20}{\sqrt{3}}×0.6\\\\&=&2400[W]\end{eqnarray}$
Δ結線負荷の部分ですが、相電圧は $V_p=線間電圧$ で、相電流 $I_p=I_2$ です。力率は $cosθ=1$ ですので、
$\begin{eqnarray}P_Δ&=&3V_pI_pcosθ\\\\&=&3×200×\displaystyle\frac{200}{r}×1\\\\&=&6936[W]\end{eqnarray}$
したがって、求める平衡三相負荷が消費する電力 $P$[kW]は、
$P=P_Y+P_Δ=2400+6936≒9.3$[kW]
答え (4)
2010年(平成22年)問9【電験理論の過去問題】
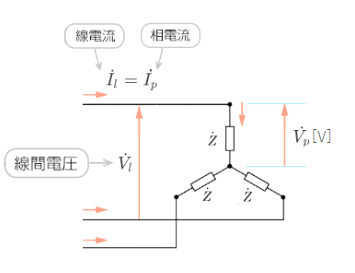
Y結線の対称三相交流電源にY結線の平衡三相抵抗負荷を接続した場合を考える。負荷側における線間電圧を $V_ℓ$〔V〕、線電流を $I_ℓ$〔A〕、相電圧を $V_p$〔V〕、相電流を $I_p$〔A〕、各相の抵抗を $R$〔Ω〕、三相負荷の消費電力を $P$〔W〕とする。
このとき、誤っているのは次のうちどれか。

三相負荷の消費電力 $P$[W]は、$P=3V_pI_pcosθ$[W]です。したがって、(4)の記述が誤りです。
答え (4)
2010年(平成22年)問15【電験理論の過去問題】
図の平衡三相回路について、次の(a)及び(b)に答えよ。
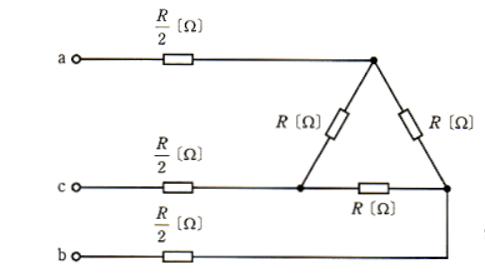
(a) 端子a,cに 100[V]の単相交流電源を接続したところ、回路の消費電力は 200[W]であった。抵抗 $R$[Ω]の値として、正しいのは次のうちどれか。
(1) 0.30 (2) 30 (3) 33 (4) 50 (5) 83
(b) 端子a,b,cに線間電圧 200[V]の対称三相交流電源を接続したときの全消費電力[kW]の値として、正しいのは次のうちどれか。
(1) 0.48 (2) 0.80 (3) 1.2 (4) 1.6 (5) 4.0
(a) Δ回路を Y 回路に変換すると、次のような等価回路になります。
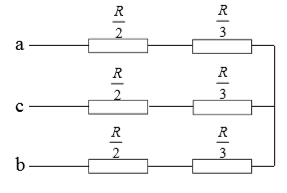
「端子a、cに 100[V]の単相交流電源を接続したところ、回路の消費電力は 200[W]であった」と、ありますので、b相は無関係となります。
a-c間の合成抵抗は $\displaystyle\frac{5R}{3}$ ですので、a-c間の消費電力を $P$[W]とすると、
$P=\displaystyle\frac{100^2}{\displaystyle\frac{5R}{3}}=200$
$R=30$[Ω]
答え (3)
(b) 端子a、b、cに線間電圧 200[V]を加えた時の相電圧 $V_p$[V]は、
$V_p=\displaystyle\frac{200}{\sqrt{3}}$
一相当たりの抵抗は、
$\displaystyle\frac{5R}{6}=\displaystyle\frac{5×30}{6}=25$[Ω]
回路で、消費される電力 $P$[W]は、
$P=3×\displaystyle\frac{(\displaystyle\frac{200}{\sqrt{3}})^2}{25}=1600$[W]
答え (4)
2011年(平成23年)問15【電験理論の過去問題】
図のように、$R$[Ω]の抵抗、静電容量 $C$[F]のコンデンサ、インダクタンス $L$[H]のコイルからなる平衡三相負荷に線間電圧 $V$[V]の対称三相交流電源を接続した回路がある。次の(a)及び(b)の問に答えよ。
ただし、交流電源電圧の角周波数は $ω$[rad/s]とする。
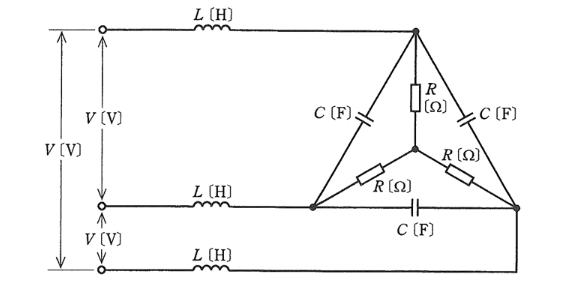
(a) 三相電源からみた平衡三相負荷の力率が1になったとき、インダクタンス $L$[H]のコイルと静電容量 $C$[F]のコンデンサの関係を示す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
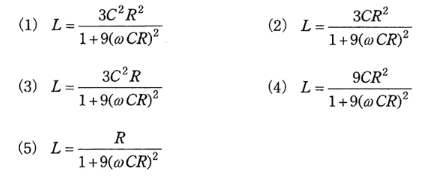
(b) 平衡三相負荷の力率が1になったとき、静電容量 $C$[F]のコンデンサの端子電圧[V]の値を示す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
(a) コンデンサをΔ⇒Y変換したときの、一相分の等価回路を示します。
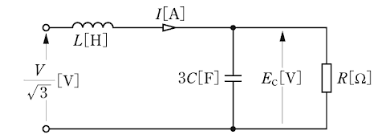
回路のインピーダンスを $\dot{Z}$[Ω]とすると、
$\begin{eqnarray}\dot{Z}&=&jωL+\displaystyle\frac{R×\displaystyle\frac{1}{jω3C}}{R+\displaystyle\frac{1}{jω3C}}\\\\&=&jωL+\displaystyle\frac{R}{1+jω3CR}\\\\&=&jωL+\displaystyle\frac{R(1-jω3CR)}{(1+jω3CR)(1-jω3CR)}\\\\&=&jωL+\displaystyle\frac{R(1-jω3CR)}{1+(ω3CR)^2}\\\\&=&\displaystyle\frac{R}{1+9(ωCR)^2}+j\left(ωL-\displaystyle\frac{3ωCR^2}{1+9(ωCR)^2}\right)\end{eqnarray}$
三相電源からみた平衡三相負荷の力率が1になるのは、虚数部が0の時ですので、
$ωL-\displaystyle\frac{3ωCR^2}{1+9(ωCR)^2}=0$
$L=\displaystyle\frac{3CR^2}{1+9(ωCR)^2}$
答え (2)
(b) コンデンサをΔ⇒Y変換したときのコンデンサと抵抗のインピーダンスを $\dot{Z_C}$[Ω]とすると、
$\dot{Z_C}=\displaystyle\frac{R×\displaystyle\frac{1}{jω3C}}{R+\displaystyle\frac{1}{jω3C}}=\displaystyle\frac{R}{1+jω3CR}$[Ω]
$Z_C=\displaystyle\frac{R}{\sqrt{1+9(ωCR)^2}}$[Ω]
平衡三相負荷の力率が1になったときの相電流 $I_p$[A]は、
$\begin{eqnarray}I_p&=&\displaystyle\frac{\displaystyle\frac{V}{\sqrt{3}}}{Z}\\\\&=&\displaystyle\frac{\displaystyle\frac{V}{\sqrt{3}}}{\displaystyle\frac{R}{1+9(ωCR)^2}}\\\\&=&\displaystyle\frac{V}{\sqrt{3}}\displaystyle\frac{1+9(ωCR)^2}{R}\end{eqnarray}$
$Z_C$ の端子電圧 $E_C$[V]は、
$\begin{eqnarray}E_C&=&I_pZ_C\\\\&=&\displaystyle\frac{V}{\sqrt{3}}\displaystyle\frac{1+9(ωCR)^2}{R}\displaystyle\frac{R}{\sqrt{1+9(ωCR)^2}}\\\\&=&\displaystyle\frac{V\sqrt{1+9(ωCR)^2}}{\sqrt{3}}[V]\end{eqnarray}$
したがって、コンデンサをY⇒Δに戻したときの端子電圧は、
$\sqrt{3}E_C=V\sqrt{1+9(ωCR)^2}$
答え (2)
2013年(平成25年)問15【電験理論の過去問題】
図1のように、周波数 50[Hz]、電圧 200[V]の対称三相交流電源に、インダクタンス 7.96[mH]のコイルと 6[Ω]の抵抗からなる平衡三相負荷を接続した交流回路がある。次の(a)及び(b)の問に答えよ。
(a) 図1において、三相負荷が消費する有効電力 $P$[W]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 1890 (2) 3280 (3) 4020 (4) 5680 (5) 9840
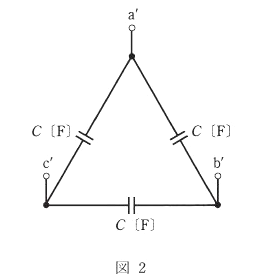
(b) 図2のように、静電容量 $C$[F]のコンデンサをΔ結線し、その端子a’,b’及びc’をそれぞれ図1の端子a,b及びcに接続した。その結果、三相交流電源からみた負荷の力率が1になった。静電容量 $C$[F]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 6.28×10-5 (2) 8.88×10-5 (3) 1.08×10-4 (4) 1.26×10-4 (5) 1.88×10-4
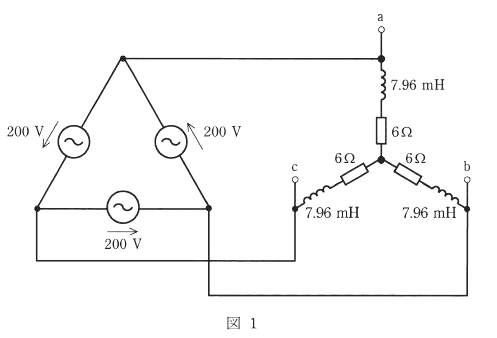
(a) コイルの誘導性リアクタンスを $X_L$[Ω]とすると、
$X_L=ωL=2×π×50×7.96×10^{-3}=2.5$[Ω]
一相分のインピーダンスの大きさを $Z$[Ω]、力率を $cosθ$ とすると、
$Z=\sqrt{6^2+2.5^2}=6.5$[Ω]
$cosθ=\displaystyle\frac{R}{Z}=\displaystyle\frac{6}{6.5}$
電源源側を、Δ⇒Y変換すると、相電圧は、$E_Y=\displaystyle \frac{E_Δ}{\sqrt{3}}$ です。相電流を $I_p$[A]とすると、
$I_p=\displaystyle\frac{E_Y}{Z}=\displaystyle\frac{\displaystyle\frac{200}{\sqrt{3}}}{6.5}=\displaystyle\frac{200}{\sqrt{3}×6.5}$[A]
三相電力は $P$[W]は、
$\begin{eqnarray}P&=&\sqrt{3}VIcosθ\\\\&=&\sqrt{3}×200×\displaystyle\frac{200}{\sqrt{3}×6.5}×\displaystyle\frac{6}{6.5}\\\\&=&5680[W]\end{eqnarray}$
答え (4)
(b) 三相無効電力を $Q$[var]とすると、
$\begin{eqnarray}Q&=&\sqrt{3}VIsinθ\\\\&=&\sqrt{3}×200×\displaystyle\frac{200}{\sqrt{3}×6.5}×\displaystyle\frac{2.5}{6.5}\\\\&=&2367[var]\end{eqnarray}$
コンデンサの三相無効電力 $Q_C$ は、Δ回路の一相当たりの3倍ですので、
$\begin{eqnarray}Q_C&=&Z_CV^2×3\\\\&=&ωCV^2×3\\\\&=&2×π×50×C×200^2×3\end{eqnarray}$
$Q=Q_C$ のとき力率が1になりますので、
$2367=2×π×50×C×200^2×3$
$C=6.28×10^{-5}$[F]
答え (1)
2014年(平成26年)問14【電験理論の過去問題】
図のように 200V の対称三相交流電源に抵抗 R[Ω]からなる平衡三相負荷を接続したところ、線電流は 1.73A であった。いま、電力計の電流コイルをc相に接続し、電圧コイルをc-a相間に接続したとき、電力計の指示 P[W]として、最も近い P の値を次の(1)~(5)のうちから一つ選べ。
ただし、対称三相交流電源の相回転はa,b,cの順とし、電力計の電力損失は無視できるものとする。
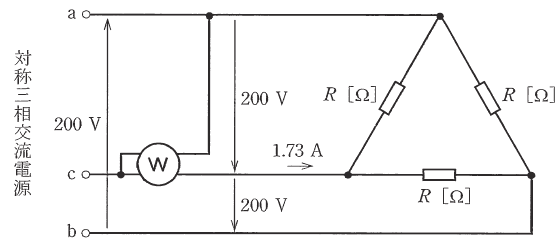
(1) 200 (2) 300 (3) 346 (4) 400 (5) 600
ベクトル図で示します。
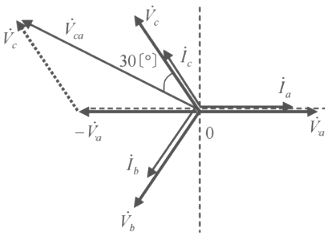
線電流 $\dot{I_C}$ は、線間電圧 $\dot{V}_{ca}$ より30°遅れとなりますので、
$\begin{eqnarray}P&=&200×1.73×cos30°\\\\&=&200×1.73×\displaystyle\frac{\sqrt{3}}{2}\\\\&≒&300[W]\end{eqnarray}$
答え (2)
2014年(平成26年)問16【電験理論の過去問題】
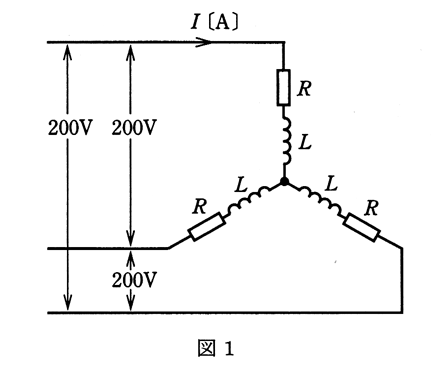
図1のように、線間電圧 200 V、周波数 50 Hzの対称三相交流電源に 1 Ωの抵抗と誘導性リアクタンス $\displaystyle\frac{4}{3}$ Ωのコイルとの並列回路からなる平衡三相負荷(Y結線)が接続されている。また、スイッチSを介して、コンデンサ $C$(Δ結線)を接続することができるものとする。次の(a)及び(b)の問に答えよ。
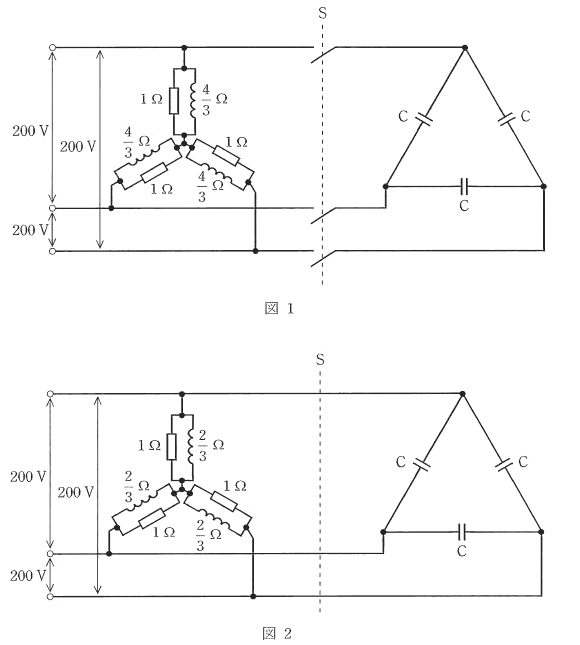
(a) スイッチSが開いた状態において、三相負荷の有効電力 $P$ の値[kW]と無効電力 $Q$ の値[kvar]の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

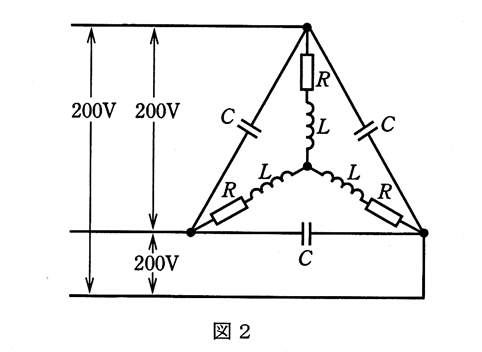
(b) 図2のように三相負荷のコイルの誘導性リアクタンスを $\displaystyle\frac{2}{3}$ Ωに置き換え、スイッチSを閉じてコンデンサ $C$ を接続する。このとき、電源からみた有効電力と無効電力が図1の場合と同じ値となったとする。コンデンサ $C$ の静電容量の値 [μF] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 800 (2) 1200 (3) 2400 (4) 4800 (5) 7200
(a) 抵抗部分に流れる電流を $I_R$[A]とすると、相電圧 $V_p$ は $V_p=\displaystyle\frac{200}{\sqrt{3}}$[V]ですので、
$I_R=\displaystyle\frac{\displaystyle\frac{200}{\sqrt{3}}}{1}=\displaystyle\frac{200}{\sqrt{3}}$
有効電力 $P$[W]は、
$P=3V_pI_R=3×\displaystyle\frac{200}{\sqrt{3}}×\displaystyle\frac{200}{\sqrt{3}}=40$[kW]
コイル部分に流れる電流を $I_L$[A]とすると、
$I_L=\displaystyle\frac{\displaystyle\frac{200}{\sqrt{3}}}{\displaystyle\frac{4}{3}}=\displaystyle\frac{150}{\sqrt{3}}$
無効電力 $Q$[W]は、
$Q=3V_pI_L=3×\displaystyle\frac{200}{\sqrt{3}}×\displaystyle\frac{150}{\sqrt{3}}=30$[kvar]
答え (1)
(b) 容量 $C$[F]のコンデンサをΔ→Y変換すると、$3C$[F]となります。電源からみた有効電力と無効電力が図1の場合と同じ値ですので、
$\displaystyle\frac{1}{3ωC}=\displaystyle\frac{4}{3}$
$C=\displaystyle\frac{1}{2π×50×4}=796$ [μF]
答え (1)
2015年(平成27年)問17【電験理論の過去問題】
図のようなV結線電源と三相平衡負荷とからなる平衡三相回路において、$R=5$Ω、$L=16$mHである。また、電源の線間電圧 $e_a$[V]は、時刻 $t$ [s] において $e_a=100\sqrt{6}sin(100πt)$[V]と表され、線間電圧 $e_b$[V]は $e_a$[V]に対して振幅が等しく、位相が 120°遅れている。ただし、電源の内部インピーダンスは零である。このとき、次の(a)及び(b)の問に答えよ。
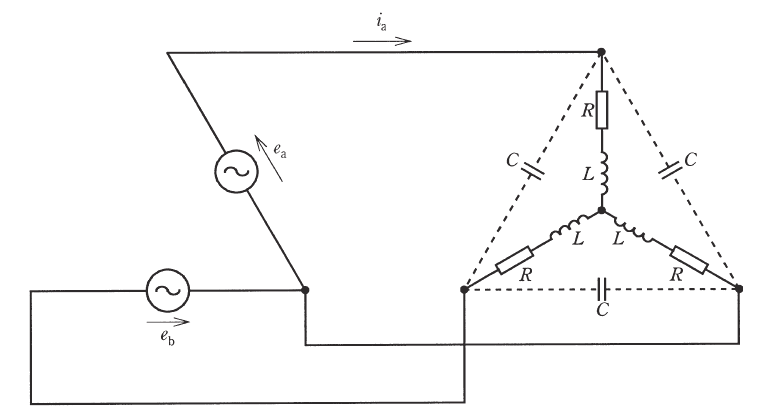
(a) 図の点線で示された配線を切断し、3個のコンデンサを三相回路から切り離したとき、三相電力 $P$ の値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 1 (2) 3 (3) 6 (4) 9 (5) 18
(b) 点線部を接続することによって同じ特性の3個のコンデンサを接続したところ $i_a$ の波形は $e_a$ の波形に対して位相が 30°遅れていた。このときのコンデンサ $C$ の静電容量の値[F]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 3.6×10-5 (2) 1.1×10-4 (3) 3.2×10-4 (4) 9.6×10-4 (5) 2.3×10-3
(a) 電源の線間電圧 $e_a=100\sqrt{6}sin(100πt)$[V]は、瞬時式を表しています。実効値 $E_{a}$[V]は $E_{a}=100\sqrt{3}$ 、周波数は $50$ となります。相電圧を $E_{Ya}$[V]とすると、
$E_{Ya}=\displaystyle\frac{E_{a}}{\sqrt{3}}=100$[V]
負荷一相分の誘導性リアクタンスを $X_L$[Ω]とすると、
$X_L=ωL=2π×50×16×10^{-3}=5$[Ω]
負荷一相分のインピーダンスを $Z$[Ω]とすると、
$Z=\sqrt{5^2+5^2}=5\sqrt{2}$
相電流を $ I_a$[A]とすると、
$ I_a=\displaystyle\frac{E_{Ya}}{Z}=\displaystyle\frac{100}{5\sqrt{2}}=10\sqrt{2}$[A]
三相電力 $P$[kW]は、
$P=3I_a^2R=3×(10\sqrt{2})^2×5=3$[kW]
答え (2)
(b) 相電圧を $E_{Ya}$[V]を基準にしたベクトル図と、コンデンサをΔ⇒Y変換したときの、一相分の等価回路を示します。
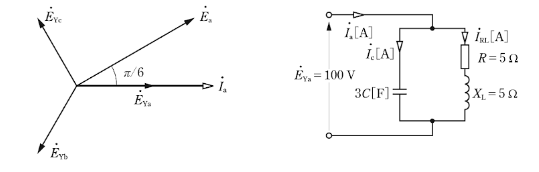
$\dot{I}_{RL}=\displaystyle\frac{100}{5+j5}=10-j10$[A]
$\dot{E}_{Ya}$ と $\dot{I}_a$ が同相になるには、$\dot{I}_{RL}$ の虚数部はコンデンサで打ち消さなければなりません。したがって、$\dot{I}_c=j10$ になります。コンデンサの容量性リアクタンスを $X_L$[Ω]とすると、
$X_C=\displaystyle\frac{E_{YC}}{I_C}=10$[Ω]
$X_C=\displaystyle\frac{1}{100π×3C}=10$[Ω]
$C=\displaystyle\frac{1}{100π×3×10}=1.1×10^{-4}$[F]
答え (2)
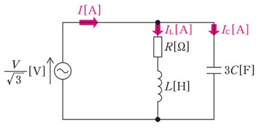
2017年(平成29年)問16【電験理論の過去問題】
図のように、線間電圧 $V$[V],周波数 $f$[Hz]の対称三相交流電源に、$R$[Ω]の抵抗とインダクタンス $L$[H]のコイルからなる三相平衡負荷を接続した交流回路がある。この回路には、スイッチSを介して、負荷に静電容量 $C$[F]の三相平衡コンデンサを接続することができる。次の(a)及び(b)の問に答えよ。
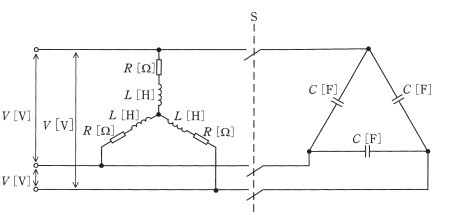
(a) スイッチSを開いた状態において、$V=200V$,$f=50Hz$,$R=5Ω$,$L=5mH$のとき、三相負荷全体の有効電力の値[W]と力率の値の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
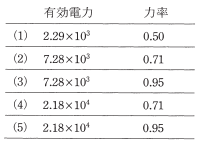
(b) スイッチSを閉じてコンデンサを接続したとき、電源からみた負荷側の力率が1になった。
このとき、静電容量 $C$ の値[F]を示す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、角周波数を $ω$[rad/s]とする。
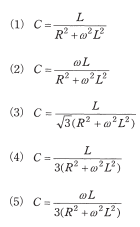
(a) コイルの誘導性リアクタンスを $X_L$[Ω]、1相あたりのインピーダンスを $Z$[Ω]とすると、
$X_L=2πfL=2×π×50×5×10^{-3}≒1.57$[Ω]
$Z=\sqrt{R^2+{X_L}^2}=\sqrt{5^2+1.57^2}≒5.24$[Ω]
力率 $cosθ$ は、
$cosθ=\displaystyle\frac{5}{5.24}≒0.95$
相電圧を $E$[V]とすると、線間電圧との関係は $E=\displaystyle\frac{V}{\sqrt{3}}$ ですので、回路に流れる電流の大きさを $I$[A]とすると、
$I=\displaystyle\frac{E}{Z}=\displaystyle\frac{\displaystyle\frac{200}{\sqrt{3}}}{5.24}≒22.04$[A]
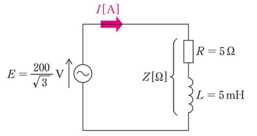
三相負荷全体の有効電力を $P$[W]とすると、
$P=3RI^2=3×5×22.04^2≒7.28×10^3$[W]
答え(3)
(b) スイッチSを閉じてコンデンサ回路を Δ⇒Y 変換し、コイルに流れる電流を $I_L$[A],コンデンサに流れる電流を $I_C$[A]とすると、
$I_L=\displaystyle\frac{\displaystyle\frac{V}{\sqrt{3}}}{\sqrt{R^2+(ωL)^2}}=\displaystyle\frac{V}{\sqrt{3(R^2+ω^2L^2)}}$[A]
$I_C=\displaystyle\frac{\displaystyle\frac{V}{\sqrt{3}}}{\displaystyle\frac{1}{ω(3C)}}=\displaystyle\frac{3ωCV}{\sqrt{3}}=\sqrt{3}ωCV$[A]
スイッチSを開いた状態の無効電力を $Q_L$[var],コイルの誘導性リアクタンスを $X_L$[Ω]とすると、
$Q_L=3X_L{I_L}^2$[var]
三相分のコンデンサの無効電力を $Q_C$[var],コンデンサの容量性リアクタンスを $X_C$[Ω]とすると、
$Q_C=3X_C{I_C}^2$[var]
スイッチSを閉じてコンデンサを接続したとき、電源からみた負荷側の力率が1になったので、回路全体の無効電力は $0$ になったことになるので、
$Q_L=Q_C$
$3X_L{I_L}^2=3X_C{I_C}^2$
$3ωL\left(\displaystyle\frac{V}{\sqrt{3(R^2+ω^2L^2)}}\right)^2=3\displaystyle\frac{1}{ω(3C)}(\sqrt{3}ωCV)^2$
$\displaystyle\frac{ωLV^2}{R^2+ω^2L^2}=\displaystyle\frac{3ω^2C^2V^2}{ωC}$
$\displaystyle\frac{L}{R^2+ω^2L^2}=3C$
$C=\displaystyle\frac{L}{3(R^2+ω^2L^2)}$
答え(4)






