第三種電気主任技術者（電験三種）試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「平行平板コンデンサの静電容量」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「平行平板コンデンサの静電容量」の過去問題も解説しています。
平行平板コンデンサ
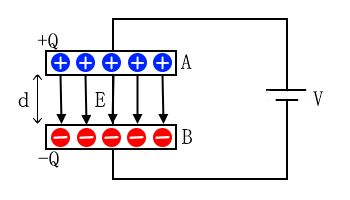
金属板ＡとＢを平行に向い合わせ、電池を接続すると、電極Ａには正の電荷が、Ｂには負の電荷が蓄えられます。
このように電荷を貯めることができる装置を「コンデンサ」といい、電荷を蓄える導体を電極または極板といい、電極が平行なものを「平行平板コンデンサ」といいます。
ここで、電極ＡとＢの面積を $S$［m2］、電極の間隔を $d$［ｍ］、電池の電圧を $V$［V］とし、電極間に $E$［V/m］の電界があるとします。
真空中の電荷 $Q$［C］から出る電気力線の総数 $ N=\displaystyle\frac{ Q }{ε_0}$［本］と考えますので、 単位面積あたりの電気力線数は、［電気力線の総数］÷［電極の表面積］となり、ガウスの法則より
$E=\displaystyle \frac{ Q }{ ε_{ 0 } }×\frac{ 1 }{S }$［本］
となります。また、電圧と電界の関係式は
$V=Ed$［V］
でした。この２式より
$Q={ ε_{ 0 } }SE=\biggl(\displaystyle\frac{ ε_{ 0 } S}{ d }\biggl)V$［C］
この式からコンデンサに蓄えられる電気量 $Q$［C］は電極間の電圧 $V$［V］に比例することがわかります。この比例定数を静電容量といい $C$（単位：ファラド［F］）とおきます。
コンデンサの静電容量 $C$ を求める公式（電極間は真空の場合）
$C=\displaystyle\frac{ ε_{ 0 } S}{ d }$［F］
$C$［F］：コンデンサの静電容量
$ε_{ 0 }$：真空の誘電率
$S$［m2］：電極の面積
$d$［ｍ］：電極間の距離
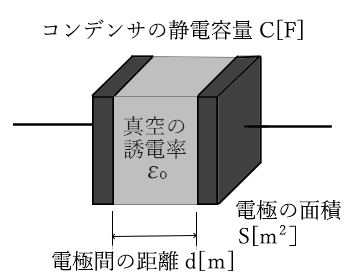
静電容量は電気量を蓄える能力を表し、電極の面積 $S$［m2］に比例し、電極の間隔を $d$［ｍ］に反比例します。
コンデンサに蓄えられる電荷
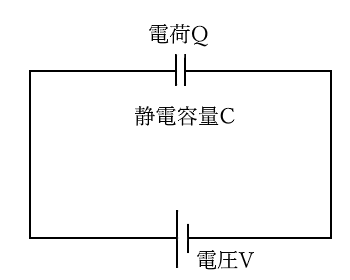
静電容量 $C$［F］のコンデンサに電圧 $V$［V］を加えると、コンデンサに電荷を蓄えることができます。その時のコンデンサに蓄えられる電荷 $Q$［C］は、次の公式で求めることができます。
コンデンサに蓄えられる電荷量 $Q$ を求める公式
$Q=CV$
$Q$［C］：コンデンサに蓄えられる電荷
$C$［F］：コンデンサの静電容量
$V$［V］：コンデンサに加える電圧
誘電率と比誘電率
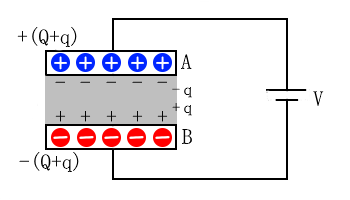
静電容量が $C$［F］のコンデンサーに電圧 $V$［V］の電池をつなぐと、極板ＡＢには $Q=CV$［C］の電荷が蓄えられます。このＡＢ間に「誘電体」をはさむと、誘電体の表面は「誘電分極」によって正電荷と負電荷が発生します。
このとき、電極ＡＢ間の電圧 $V$ と電界 $E$ は変化しませんので、誘電体の表面に発生した正電荷と負電荷を打ち消すために、電池から電荷が供給されます。
誘電体を電極間にはさむことにより、極板に蓄えることができる電荷量を $Q+q$［C］に増やすことができます。その結果、静電容量が増加するというわけです。
増加する割合は、間にはさむ誘電体の種類によって異なります。誘電分極をしやすい物質ほど電荷量を増やすことができます。この誘電分極のしやすさのことを「誘電率」といい、$ε$（読み：イプシロン）［F/m］で表します。
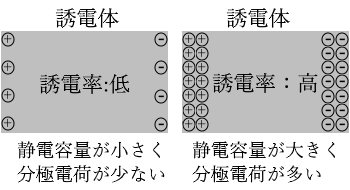
誘電分極をしやすい物質は $ε$［F/m］の値が大きくなり、静電容量 $C$［F］の値も大きくなります。静電容量 $C$［F］が大きいほど、電荷を多く溜めることができます。
誘電率は誘電体の種類によって異なるのですが、通常は誘電率を数値として使いません。誘電の度合いを示す数値としては、真空の誘電率との比を使って表します。その比を「比誘電率」といい。$ε_r$（イプシロンアール）で表します。
誘電率の公式
$ε_{ r }=\displaystyle\frac{ ε }{ ε_{ 0 } }$
$ε={ ε_{ r } }{ ε_{ 0 } }$
$ε$［F/m］：誘電率
$ε_0$［F/m］：真空の誘電率
$ε_r$：比誘電率
平行板コンデンサの静電容量 $C$［F］は、
$C=\displaystyle\frac{ ε_{ r } ε_{ 0 } S}{ d }$［F］
で表され、通常はこの式を使います。
電験三種－理論の過去問解説：「静電気分野－平行平板コンデンサの静電容量」
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
2010年（平成22年）問2【電験理論の過去問題】
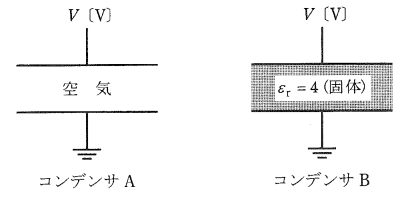
図に示すように、電極板面積と電極板間隔がそれぞれ同一の２種類の並行平板コンデンサがあり、一方を空気コンデンサＡ、他方を個体誘電体（比誘電率 εr=4 ）が満たされたコンデンサＢとする。両コンデンサにおいて、それぞれ一方の電極に直流電圧 V［V］を加え、他方の電極を接地したとき、コンデンサＢの内部電界［V/m］及び電極板上に蓄えられた電荷［C］はコンデンサＡのそれぞれ何倍となるか。その倍率として、正しいものを組み合わせたのは次のうちどれか。
ただし、空気の比誘電率を1とし、コンデンサの端効果は無視できるものとする。
| 内部電界 | 電荷 | |
|---|---|---|
| (1) | 1 | 4 |
| (2) | 4 | 4 |
| (3) | $\displaystyle\frac{1}{ 4 }$ | 4 |
| (4) | 4 | 1 |
| (5) | 1 | 1 |
両コンデンサの電極板面積と電極板間隔がそれぞれ同一で、両コンデンサに直流電圧 V［V］を加えることから、V=Edより、両コンデンサの内部電界 E［Ｖ/ｍ］は同一の値になります。
Ａ，Ｂのコンデンサの静電容量を CA，CB とすると、
$C_{ A}=\displaystyle\frac{ε_{ 0 } S}{ d }$
$C_{ B}=\displaystyle\frac{ ε_{ r } ε_{ 0 } S}{ d }＝4×\frac{ε_{ 0 } S}{ d }=4C_{ A}$
答え (1)
2015年（平成27年）問1【電験理論の過去問題】
平行平板コンデンサにおいて、極板間の距離，静電容量，電圧，電界をそれぞれ d［m］，C［F］，V［V］，E［V/m］、極板上の電荷を Q［C］とするとき、誤っているものを次の(1)～(5)のうちから一つ選べ。
ただし、極板の面積及び極板間の誘電率は一定であり、コンデンサの端効果は無視できるものとする。
- Q を一定として d を大きくすると、C は減少する。
- Q を一定として d を大きくすると、E は上昇する。
- Q を一定として d を大きくすると、V は上昇する。
- V を一定として d を大きくすると、E は減少する。
- V を一定として d を大きくすると、Q は減少する。
電圧と電界の関係式
$V=Ed$［V］ ・・・①
平行平板コンデンサの静電容量
$C=\displaystyle\frac{ ε_{ r } ε_{ 0 } S}{ d }$ ・・・②
電荷と電圧の関係式
$Q=CV$ ・・・③
- ①、③式より 正しい
- ①、③式より 誤り
- ②、③式より 正しい
- ①式より 正しい
- ②、③式より 正しい
答え (2)
2016年（平成28年）問2【電験理論の過去問題】
極板Aと極板Bとの間に一定の直流電圧を加え、極板Bを接地した平行板コンデンサに関する記述a～dとして、正しいものの組合せを次の(1)～(5)のうちから一つ選べ。ただし、コンデンサの端効果は無視できるものとする。
- 極板間の電位は、極板Aからの距離に対して反比例の関係で変化する。
- 極板間の電界の強さは、極板Aからの距離に対して一定である。
- 極板間の等電位線は、極板に対して平行である。
- 極板間の電気力線は、極板に対して垂直である。
- a
- b
- a、c、d
- b、c、d
- a、b、c、d
図で考えるとわかりやすいと思います。
- 極板A から距離 $x$ 地点の電位 は、 $V=E(d-x)$［V］となり、 反比例とはなりません。
- 一様な電界の定義から 正しい
- 等電位線の定義から正しい
- 電気力線の定義から正しい
答え (4)
2016年（平成28年）問17【電験理論の過去問題】
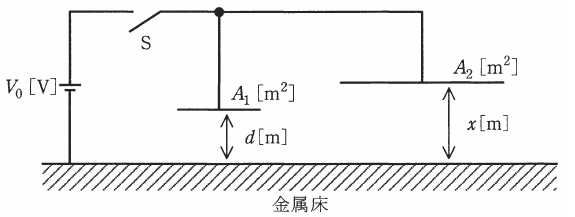
図のように、十分大きい平らな金属板で覆われた床と平板電極とで作られる空気コンデンサが二つ並列接続されている。二つの電極は床と平行であり、それらの面積は左側が A1＝10-3m2、右側が A2＝10-2m2 である。床と各電極の間隔は左側が d＝10-3m で固定、右側がx [m] で可変、直流電源電圧は V0＝1000V である。次の(a)及び(b)の問に答えよ。
ただし空気の誘電率をε＝8.85×10-12F/mとし、静電容量を考える際にコンデンサの端効果は無視できるものとする。
(a) まず、右側の x [m] を d [m] と設定し、スイッチSを一旦閉じてから開いた。このとき、二枚の電極に蓄えられる合計電荷 Q の値 [C] として最も近いものを次の(1)～(5)のうちから一つ選べ。
(1) 8.0×10-9 (2) 1.6×10-8 (3) 9.7×10-8 (4) 1.9×10-7 (5) 1.6×10-6
(b) 上記(a)の操作の後、徐々にxを増していったところ、x＝3.0×10-3m のときに左側の電極と床との間に火花放電が生じた。左側のコンデンサの空隙の絶縁破壊電圧Vの値 [V] として最も近いものを次の(1)～(5)のうちから一つ選べ。
(1) 3.3×102 (2) 2.5×103 (3) 3.0×103 (4) 5.1×103 (5) 3.0×104
(a) 左側と右側の静電容量をそれぞれ C1，C2、電荷を Q1，Q2 とすれば、
$\begin{eqnarray}C_1&=&\displaystyle\frac{εA_1}{d}\\\\&=&\displaystyle\frac {8.85×10^{-12}×1×10^{-3}}{1×10^{-3}}\\\\&=& 8.85×10^{-12}［F］\end{eqnarray}$
$\begin{eqnarray}C_2&=&\displaystyle\frac{εA_2}{d}\\\\&=& \displaystyle\frac {8.85×10^{-12}×1×10^{-2}}{1×10^{-3}}\\\\&=& 8.85×10^{-11}［F］\end{eqnarray}$
$\begin{eqnarray}Q_1&=&C_1V\\\\&=&8.85×10^{-12}×1000\\\\&=&8.85×10^{-9}［C］\end{eqnarray}$
$\begin{eqnarray}Q_2&=&C_2V\\\\&=&8.85×10^{-11}×1000\\\\&=&8.85×10^{-8}［C］\end{eqnarray}$
合成電荷 Q［C］は、
$\begin{eqnarray}Q&=&Q_1+Q_2\\\\&=&8.85×10^{-9}+8.85×10^{-8}\\\\&≒&9.7×10^{-8}［C］\end{eqnarray}$［C］
答え (3)
(b) 静電容量は、電極の面積 A［m2］に比例し、電極の間隔を x［ｍ］に反比例しますので、距離が 3倍になった時の静電容量 C2‘ は、
$C_2’=\displaystyle\frac{C_2}{3}$
$\begin{eqnarray}V&=&\displaystyle\frac{Q_1+Q_2}{C_1+\displaystyle\frac{C_2}{3}}\\\\&=&\displaystyle\frac{3(Q_1+Q_2)}{3C_1+C_2}\\\\&=&\displaystyle\frac{3×9.7×10^{-8}}{3×8.85×10^{-9}+8.85×10^{-8}}\\\\&=&2.5×10^3\end{eqnarray}$
答え (2)
電験三種の理論科目に出題される「静電気分野」のページ
１.クーロンの法則とは
２.電界とガウスの法則
３.静電界中の電位と電圧
４.静電誘導と誘電分極
５.平行平板コンデンサの静電容量
６.コンデンサの直列接続と並列接続
７.静電エネルギー
８.誘電体とコンデンサ
９.導体球と同心球導体の静電容量
