復水器の損失計算と重油の燃焼

このページでは、復水器の損失計算と重油の燃焼について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の電力科目の試験で、実際に出題された、復水器の損失計算と重油の燃焼の過去問題も解説しています。

復水器の損失計算

冷却に海水を使用する復水器は、冷却水に持ち去られる熱量が海に捨てられます。その捨てられた熱量は、損失となります。

定格出力 1000［kw］の発電機が効率 98［％］で運転しているとします。タービンの熱消費率は 8,000［KJ/(KW･h)］としたとき、復水器冷却水が持ち去る熱量を計算してみます。

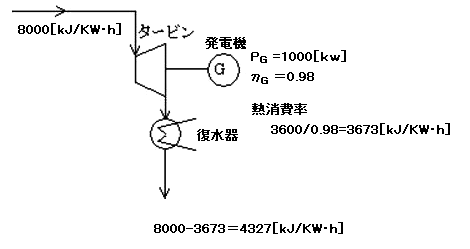
電力量 1［kWh］を蒸発させるための熱量は 3600［kJ］です。タービンの熱消費率は 8,000［KJ/(KW･h)］ですので、タービン入口の熱量 8000［kJ/KW･h］に対して、発電機への熱量は 3600/0.98=3673［kJ/KW･h］になります。

この差 8000-3673＝4327［kJ/KW･h］が、復水器が持ち去る 1KW当たりの単位時間熱量となります。発電機出力は 1000［kW］で運転していますので、復水器冷却水が持ち去る熱量は、

4327［kJ/KW･h］× 1000［KW］

= 4327000［kJ/ｈ］

= 4327000/3600［kJ/s］= 1202［kJ/s］

となります。

海水の比熱を c［kJ/(kg⋅K)］、海水の密度を ρ［kg/m³］、復水器冷却水流量を W［m³/s］、冷却水の温度上昇を ΔT［K］とすると、復水器冷却水が持ち去る熱量 q［kJ/s］は、次式で与えられます。

重油の燃焼

二酸化炭素の発生量

重油が燃焼したときの CO2 の発生量を計算してみます。

炭素の燃焼化学式は
   C + O2 → CO2

これを原子量で表すと、
  12 + 16×2 → 44

この式は、炭素 12g がすべて燃えると、44ｇ の二酸化炭素が発生することを意味しています。では、重油 1000［kg］を燃やした場合に発生する二酸化炭素は、

  1000［kg］× 85［％］× 44/12 ＝ 3117［kg］

の二酸化炭素が発生します。

必要空気量

重油の燃焼に必要な空気量を計算してみます。

重油の燃焼の化学式は
  C + O2 → CO2
  2H2 + O2 → 2H2O

これを原子量で表すと、
  Cの燃焼　：　12 + 16×2 → 44
  Hの燃焼　：　2×1×2 + 16×2 → 36

つまり
  炭素 C を 1［kg］燃焼させるためには、32/12［kg］の酸素 O が必要 です。
  水素 H を 1［kg］燃焼させるためには、32/4［kg］の酸素Oが必要 です。

O2 の分子量は 32 ですので、燃料 1kg 中の炭素を C［kg］、水素を H［kg］とすると、理論酸素量［kmol/kg］は、次式で表すことができます。

空気の酸素濃度は 21［％］で、1mol の気体標準状態の体積は 22.4［ℓ］ですので、理論空気量［ｍ³］は次式で表すことができます。

$\begin{eqnarray}理論空気量&=&\displaystyle \frac{ 22.4}{ 0.21}×\left(\displaystyle \frac{ C}{ 12}+\displaystyle \frac{ H}{ 4}\right)\\\\&=&\displaystyle \frac{ 22.4}{ 0.21}×\left(\displaystyle \frac{ 1000×0.85}{ 12}+\displaystyle \frac{ 1000×0.15}{ 4}\right)\\\\&=&11555\end{eqnarray}$

速度調定率

速度調定率 R とは、発電機出力の変化率に対する回転数の変化率の割合のことです。ある出力で運転中の発電機の負荷を変化させたとき、「発電機負荷の変化分」に対する「回転速度の変化分」の比のことをいいます。

回転速度 N［min^-1］と周波数 f［Hz］は、$N=\displaystyle \frac{ 120f}{ p}$ の関係がありますので、速度調定率 R は、次の式でも表わせます。（ p は極数）

　　

電験三種－電力（火力発電）過去問題

1997年（平成9年）問11

水力発電所と重油専焼汽力発電所とによって、需要端において最大電力 100［MW］、年負荷率 60［%］の負荷に電力を供給する場合、水力発電所の出力を 50［MW］、年利用率を 75［%］とすれば、汽力発電所における重油の消費量［kl］は年間いくら必要となるか。次の値のうちから正しいものを選べ。
ただし、燃料消費量は 0.24［l/kWh］とし、発電所から需要端までの送電損失や発電所内損失は考えないものとする。

(1) 184　(2) 47300　(3) 197100　(4) 328500　(5) 525600

1997年（平成9年）問11　過去問解説

需要端に送らなければならない年間電力量 W は、

W=365×24×100×0.6=525600［MWh］

この内、水力発電所が供給する年間電力量 W_w は、

W_w=365×24×50×0.75=328500［MWh］

よって、汽力発電所の年間電力量 W_f は、

W_f=W-W_w=525600-328500=197100［MWh］

G=197100×10³［kWh］×0.24［l/kWh］=47300［kl］

答え（２）

1999年（平成11年）問11

速度調定率 4［%］のタービン発電機が系統に並列され、定格出力 600［MW］、定格出力周波数 60［Hz］で運転している。系統周波数が 60.2［Hz］に急上昇したときの発電機出力［MW］の値として、正しいのは次のうちどれか。
ただし、速度調定率は次式で表される。

(1) 500　(2) 550 　(3) 600　 (4) 650　 (5) 700

1999年（平成11年）問11　過去問解説

速度調定率の公式より

$4=\displaystyle \frac{ \displaystyle \frac{ 60.2-60}{ 60}}{ \displaystyle \frac{ 600-P_2}{ 600}}$

$P_2=550$［MW］

答え（２）

2002年（平成14年）問11

タービン出力 700［MW］で運転している汽力発電所があり、復水器の冷却に海水を使用している。このときの復水器冷却水の流量は 30［ｍ³/s］、タービンの熱消費率は 8,000［KJ/(KW･h)］、海水の比熱容量は 4.0［KJ/(Kg･K)］、海水の密度は 1.1×10³［Kg/ｍ³］である。この復水器について、次の(a)及び(b)に答えよ。
ただし、復水器冷却水が持ち去る熱以外の損失は無視するものとする。

(a) 復水器冷却水が持ち去る毎時の熱量[KJ/h]の値として、最も近いのは次のうちどれか。

(1) 2.5×10⁶(2) 3.1×10⁶　(3) 5.6×10⁶　(4) 3.1×10⁹　(5) 5.6×10⁹

(b) 復水器冷却水の温度上昇[Ｋ]の値として、最も近いのは次のうちどれか。

(1) 5.3　(2) 6.5　(3) 7.9　(4) 12　(5) 23

2002年（平成14年）問11　過去問解説

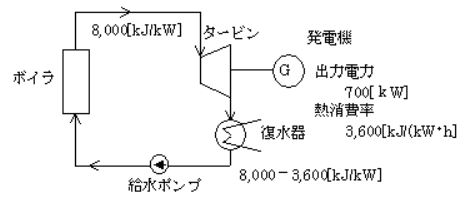
(a) 電力量 1［kWh］を蒸発させるための熱量は 3600［kJ］です。タービンの熱消費率は 8000［KJ/(KW･h)］ですので、タービン入口の熱量 8000［kJ/KW･h］に対して、発電機への熱量は 3600［kJ/KW･h］になります。

この差が 8000-3600＝4400［kJ/KW･h］が、復水器冷却水が持ち去る 1KW 当たりの単位時間熱量となります。出力は 700［MW］で運転中ですので、復水器冷却水が持ち去る単位時間熱量は、

4400［kJ/KW･h］×700×10³［KW］＝3.08×10⁹［kJ/h］

答え (4)

(b) q=cρWΔT［kJ/s］より

$\displaystyle \frac{ 3.08×10^9}{ 3600}=4.0×1.1×10^3×30×ΔT$

$ΔT=6.5$［K］

答え (2)

2005年（平成17年）問15

重油専燃火力発電所が出力 1000［MW］で運転しており、発電端効率が 41［％］、重油発熱量が 44000［kJ/kg］であるとき、次の(a)及び(b)に答えよ。
ただし、重油の化学成分（重量比）は炭素 85［%］、水素 15［%］、炭素の原子量は 12、酸素の原子量は 16とする。

(a) 重油消費量［t/h］の値として、最も近いものは次のうちどれか。

(1) 50　(2) 80　(3) 120　(4) 200　(5) 250

(b) １日に発生する二酸化炭素の重量［t］の値として、最も近いのは次のうちどれか。

(1) 9.5×10³　(2) 12.8×10³　(3) 15.0×10³　(4) 17.6×10³　(5) 28.0×10³

2005年（平成17年）問15　過去問解説

(a) 燃料消費量を B［kg/h］、燃料の発熱量を H［kJ/kg］、発電機出力を P_G［kW］、発電端熱効率を η_P とすると、

$η_P=\displaystyle \frac{ 3600P_G}{ BH}×100$［%］

$41=\displaystyle \frac{ 3600×1000×10^3}{ 44000×H}×100$［%］

$H=200000$［kg］

答え (4)

(b) 1日に使用する炭素量は

200［t］×24［h］×0.85＝4080［t］

1日に使用する酸素量［t］は、反応式、C + O₂ → CO₂ を、原子量で換算すると、12+16×2 → 44 ですので、 

4080［t］×(16×2)/12＝10880［t］

二酸化炭素の重量［t］は

4080［t］+10880［t］＝14960［ｔ］

答え (3)

2006年（平成18年）問15

復水器での冷却に海水を使用する汽力発電所が出力 600［MW］で運転しており、復水器冷却水量が 24［m³/s］、冷却水の温度上昇が 7［℃］であるとき、次の(a)及び(b)に答えよ。
ただし、海水の比熱を 4.02［kJ/(kg・K)］ 、密度を 1.02×10³［kg/m³］、発電機効率を 98［%］とする。

(a) 復水器で海水へ放出される熱量［kJ/s］の値として、最も近いのは次のうちどれか。

(1) 4.25×10⁴　(2) 1.71×10⁵　(3) 6.62×10⁵　(4) 6.89×10⁵　(5) 8.61×10⁵

(b) タービン室効率［%］の値として、最も近いのは次のうちどれか。
ただし、条件を示していない損失は無視できるものとする。

(1) 41.5　(2) 46.5　(3) 47.0　(4) 47.5　(5) 48.0

2006年（平成18年）問15　過去問解説

(a) q=cρWΔT［kJ/s］より

q=4.02×1.02×10³×24×7=6.89×10⁵ ［kJ/s］

答え (4)

(b) タービン出力を P_T、発電機出力を P_G、発電機効率を η_G とすると、

$η_G=\displaystyle \frac{ P_G}{ P_T}×100$［%］

$98=\displaystyle \frac{ 600}{ P_T}×100$

$P_T＝612$［MW］

タービン室効率 η_TR とすると、タービン入力はタービン出力+復水器で海水へ放出される熱量なので、

$η_{TR}=\displaystyle \frac{ 612}{ 612+689}×100≒47.0$［%］

答え (3)

2007年（平成19年）問15

定格出力 1000［ＭＷ］、速度調定率 5［％］のタービン発電機と、定格出力 300［ＭＷ］、速度調定率 3［%］の水車発電機が電力系統に接続されており、タービン発電機は 100［％］負荷、水車発電機は 80［%］負荷をとって、定格周波数（50［㎐］）にて並行運転中である。
負荷が急変し、タービン発電機の出力が 600［ＭＷ］で安定したとき、次の(a)及び(b)に答えよ。

(a)このときの系統周波数［㎐］の値として、最も近いのは次のうちどれか。
ただし、ガバナ特性は直線とする。なお、速度調定率は次式で表される。

(1) 49.5　(2) 50.0　(3) 50.3　(4) 50.6　(5) 51.0

(b) このときの水車発電機の出力［ＭＷ］の値として、最も近いのは次のうちどれか。

(1) 40　(2) 80　(3) 100　(4) 120　’5) 180

2007年（平成19年）問15　過去問解説

(a) 速度調定率の公式より

$5=\displaystyle \frac{ \displaystyle \frac{ f_2-50}{ 50}}{ \displaystyle \frac{ 1000-600}{ 1000}}$

$ f_2=51$［㎐］

答え (5)

(b) 水車発電機の定格出力 300［ＭＷ］で 80［%］負荷をとっているので、初期出力は 240［ＭＷ］となります。速度調定率の公式より

$3=\displaystyle \frac{ \displaystyle \frac{ 51-50}{ 50}}{ \displaystyle \frac{ 240-P_2}{ 300}}$

$P_2=40$［ＭＷ］

答え (1)

2009年（平成21年）問15

最大出力 600［MW］の重油専燃火力発電所がある。重油の発電量は 44000［kJ/kg］で、潜熱は無視するものとして、次の(a)及び(b)に答えよ。

(a) 45000［MW・ｈ］の電力量を発生するために、消費された重油の量が 9.3×10³［t］であるときの発電端効率［％］の値として、最も近いのは次のうちどれか。

(1) 37.8　(2) 38.7　(3) 39.6　(4) 40.5　(5) 41.4

(b) 最大出力で 24時間運転した場合の発電端効率が 40.0［％］であるとき、発生する二酸化炭素の量［t］として、最も近い値は次のうちどれか。
なお、重油の化学成分は重量比で炭素 85.0［％］、水素 15.0［％］、原子量は炭素 12、酸素 16とする。炭素の酸化反応は次のとおりである。

C + O2 → CO2

(1) 3.38×10²　(2) 6.83×10²　(3) 8.03×10²　(4) 9.18×10³　(5) 1.08×10⁴

2009年（平成21年）問15　過去問解説

(a) 燃料消費量を B［kg/h］、燃料の発熱量を H［kJ/kg］、発電機出力を P_G［kW］、発電端熱効率を η_P とすると、

$η_P=\displaystyle \frac{ 3600P_G}{ BH}×100$［%］

$η_P=\displaystyle \frac{ 3600×45000×10^3}{ 9.3×10^3×44000}×100≒39.6$［%］

答え (3)

(b) 最大出力で 24時間運転した場合の、発電機出力 P_G［kW］は、

$P_G=600×10^3×24=14400$［kW］

発電端効率が 40.0［％］であるので、

$0.4=\displaystyle \frac{ 3600×14400}{ B×44000}$

$B≒2.945×10^6$［kg］

使用した炭素の量［t］は 、

2.945×10⁶×0.85≒2.503×10⁶［kg］≒ 2.503×10³［ｔ］

使用した酸素量［t］は、反応式、C + O₂ → CO₂ を、原子量 で換算すると、12 + 16×2 → 44 ですので、 

2.503 × 10³［t］×（16×2)/12 ≒ 6.675×10³［t］

二酸化炭素の重量［t］は

2.503×10³［t］+ 6.675×10³［t］＝ 9.178×10³［t］

答え (4)

2011年（平成23年）問15

定格出力 500［MW］、定格出力時の発電端熱効率 40［％］の汽力発電所がある。重油の発熱量は 44000［kJ/kg］で、潜熱の影響は無視できるものとして、次の(a)及び(b)の問に答えよ。
ただし、重油の化学成分を炭素 85［％］、水素 15［％］、水素の原子量を 1、炭素の原子量を 12、酸素の原子量を 16、空気の酸素濃度を 21［％］とし、重油の燃焼反応は次のとおりである。

C　+　Ｏ２　→　ＣＯ２

2H2　+　O2 　→　２H２Ｏ

(a) 定格出力にて、1時間運転したときに消費する燃料重量［t］の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 10　(2) 16　(3) 24　(4) 41　(5) 102

(b) このとき使用する燃料を完全燃焼させるために必要な理論空気量※［㎥］の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし 1［mol］の気体標準状態の体積は 22.4［ｌ］とする。
※理論空気量：燃料を完全に燃焼するために必要な最小限の空気量（標準状態における体積）

(1) 5.28×10⁴　(2) 1.89×10⁵　(3) 2.48×10⁵　(4) 1.18×10⁶　(5) 1.59×10⁶

2011年（平成23年）問15　過去問解説

(a) 燃料消費量を B［kg/h］、燃料の発熱量を H［kJ/kg］、発電機出力を P_G［kW］、発電端熱効率を η_P とすると、

$η_P=\displaystyle \frac{ 3600P_G}{ BH}$

$η_P=\displaystyle \frac{ 3600×500×10^3}{ B×44000}$

B ≒ 102000［kg/h］≒ 102［t/h］

答え (5)

(b) 理論空気量の公式より、

$\begin{eqnarray}理論空気量&=&\displaystyle \frac{ 22.4}{ 0.21}×\left(\displaystyle \frac{ C}{ 12}+\displaystyle \frac{ H}{ 4}\right)\\\\&=&\displaystyle \frac{ 22.4}{ 0.21}×\left(\displaystyle \frac{ 102×10^3×0.85}{ 12}+\displaystyle \frac{ 102×10^3×0.15}{ 4}\right)\\\\&≒&1.18×10^6\end{eqnarray}$

答え (4)

2013年（平成25年）問15

復水器の冷却に海水を使用する汽力発電所が定格出力で運転している。次の(a)及び(b)の問に答えよ。

(a) この発電所の定格出力運転時には発電端熱効率が 38［％］、燃料消費量が 40［t/h］ である。1時間当たりの発生電力量［MW・h］の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし、燃料発電量は 44000 ［kJ/kg］とする。

(1) 186　(2) 489　(3) 778　(4) 1286　(5) 2046

(b) 定格出力で運転を行った時、復水器冷却水の温度上昇を 7［K］とするために必要な復水器冷却水の流量［m³/s］の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし、タービン熱消費率を 8000 ［kJ/(kW・h)］、海水の比熱と密度をそれぞれ 4.0［kJ/(kg・K)］，1.0 × 10³ ［kg/m3］、発電機効率を 98 ［％］ とし、提示していない条件は無視する。

(1) 6.8　(2) 8.0　(3) 14.8　(4) 17.9　(5) 21.0

2013年（平成25年）問15　過去問解説

(a) 燃料消費量を B［kg/h］、燃料の発熱量を H［kJ/kg］、発電機出力を P_G［kW］、発電端熱効率を η_P とすると、

$η_P=\displaystyle \frac{ 3600P_G}{ BH}$

$0.38=\displaystyle \frac{ 3600P_G}{ 40×10^3×44000}$

$P_G=186$［MW・h］

答え (1)

(b) タービン出力を P_T、発電機効率 η_G とすると、

$η_G=\displaystyle \frac{ P_G}{ P_T}$

$0.98=\displaystyle \frac{ 186}{ P_T}$

$ P_T≒190$［MW・h］=190×10³［kW・ｈ］

電力量 1［kWh］を蒸発させるための熱量は 3600［kJ］です。タービンの熱消費率は 8000［KJ/(KW･h)］ですので、タービン入口の熱量 8000［kJ/KW･h］に対して、発電機への熱量は 3600/0.98=3673［kJ/KW･h］になります。

この差が 8000-3673＝4327［kJ/KW･h］が、復水器冷却水が持ち去る 1［kW］当たりの単位時間熱量となります。発電機出力は 186［kW］で運転していますので、復水器冷却水が持ち去る熱量は、

4327［kJ/KW･h］×186×10³［KW］≒8.05×10⁸［kJ/ｈ］

q=cρWΔT［kJ/s］より

$\displaystyle \frac{ 8.05×10^8}{ 3600}≒4.0×1.0×10^3×W×7$

W≒7.98［m³/s］

答え (2)

2014年（平成26年）問17

定格出力 200MW の石炭火力発電所がある。石炭の発熱量は 28000kJ/kg、定格出力時の発電端熱効率は 36% で、計算を簡単にするため潜熱の影響は無視するものとして、次の(a)及び(b)の問に答えよ。
ただし、石炭の化学成分は重量比で炭素 70%、水素他 30%、炭素の原子量を 12、酸素の原子量を 16とし、
炭素の酸化反応は次のとおりである。

C　+　O₂　→　CO₂

(a) 定格出力にて 1日運転したときに消費する燃料重量の値［t］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 222　(2) 410　(3) 1062　(4) 1714　(5) 2366

(b) 定格出力にて1日運転したときに発生する二酸化炭素の重量の値［t］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 327　(2) 1052　(3) 4399　(4) 5342　(5) 6285

2014年（平成26年）問17　過去問解説

(a) 燃料消費量を B［kg/h］、燃料の発熱量を H［kJ/kg］、発電機出力を P_G［kW］、発電端熱効率を η_P とすると、

$η_P=\displaystyle \frac{ 3600P_G}{ BH}$

$0.36=\displaystyle \frac{ 3600×200×10^3}{ B×28000}$

$B=71428.6$［kg/h］=$71428.6×24=1714$［t/日］

答え (4)

(b) 定格出力にて1日運転したときに発生する炭素の重量を C［t］とすると、炭素は 70%ですので、

C = 1714［t/日］×70［%］≒ 1200［t/日］

反応式、C + O₂ → CO₂ を、原子量で換算すると、12 + 16×2 → 44 ですので、 1日運転したときに発生する二酸化炭素の重量［t］は、

1200［t/日］+ 3200［t/日］→ 4400［t/日］

答え (3)

2015年（平成27年）問15

定格出力 1000MW、速度調定率 5％のタービン発電機と、定格出力 300MW、速度調定率 3％の水車発電機が周波数調整用に電力系統に接続されており、タービン発電機は 80％出力、水車発電機は 60％出力をとって、定格周波数（60Hz）にてガパナフリー運転を行っている。
系統の負荷が急変したため、タービン発電機と水車発電機は速度調定率に従って出力を変化させた。次の(a)及び(b)の問に答えよ。
ただし、このガパナフリー運転におけるガバナ特性は直線とし、次式で表される速度調定率に従うものとする。また、この系統内で周波数調整を行っている発電機はこの 2台のみとする。

(a) 出力を変化させ、安定した後のタービン発電機の出力は 900MWとなった。このときの系統周波数の値 [Hz] として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 59.5　(2) 59.7　(3) 60　(4) 60.3　(5) 60.5

(b) 出力を変化させ、安定した後の水車発電機の出力の値 [MW] として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 130　(2) 150　(3) 180　(4) 210　(5) 230

2015年（平成27年）問15　過去問解説

(a) 速度調定率の公式より

$5=\displaystyle \frac{ \displaystyle \frac{ f_2-60}{ 60}}{ \displaystyle \frac{ (1000×0.8)-900}{ 1000}}$

$ f_2=59.7$［㎐］

答え (2)

(b) 速度調定率の公式より

$3=\displaystyle \frac{ \displaystyle \frac{ 59.7-60}{ 60}}{ \displaystyle \frac{ (300×0.6)-P_2}{ 300}}$

$ P_2=230$［MW］

答え (5)

2017年（平成29年）問15

定格出力 600MW、定格出力時の発電端熱効率 42%の汽力発電所がある。重油の発熱量は 44000kJ/kgで、潜熱の影響は無視できるものとして、次の(a)及び(b)の問に答えよ。
ただし、重油の化学成分は質量比で炭素 85%、水素 15%、水素の原子量を 1、炭素の原子量を 12、酸素の原子量を 16、空気の酸素濃度を 21%とし、重油の燃焼反応は次のとおりである。

C　+　O₂　→　CO₂

2H₂　+　O₂ 　→　2H₂O

(a) 定格出力にて、1日運転したときに消費する燃料質量の値［t］として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(1) 117　(2) 495　(3) 670　(4) 1403　(5) 2805

(b) そのとき使用する燃料を完全燃焼させるために必要な理論空気量※の値 [m³] として、最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし、1molの気体標準状態の体積は 22.4Lとする。
※理論空気量：燃料を完全に燃焼するために必要な最小限の空気量(標準状態における体積)

(1) 6.8×10⁶　(2) 9.2×10⁶　(3) 32.4×10⁶　(4) 43.6×10⁶　(5) 87.2×10⁶

2017年（平成29年）問15　過去問解説

(a) 燃料消費量を B［kg/h］、燃料の発熱量を H［kJ/kg］、発電機出力を P_G［kW］、発電端熱効率を η_P とすると、

$η_P=\displaystyle \frac{ 3600P_G}{ BH}$

$0.42=\displaystyle \frac{ 3600×600×10^3}{ B×44000H}$

B ≒ 116900［kg/h］≒ 116900×24 ≒ 2806［t/日］

答え (5)

(b) 理論空気量の公式より、

$\begin{eqnarray}理論空気量&=&\displaystyle \frac{ 22.4}{ 0.21}×\left(\displaystyle \frac{ C}{ 12}+\displaystyle \frac{ H}{ 4}\right)\\\\&=&\displaystyle \frac{ 22.4}{ 0.21}×\left(\displaystyle \frac{ 2806×10^3×0.85}{ 12}+\displaystyle \frac{ 2806×10^3×0.15}{ 4}\right)\\\\&≒&32.4×10^6\end{eqnarray}$

答え (3)