このページでは、ケーブルの静電容量と線路定数について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の電力科目の試験で、実際に出題されたケーブルの静電容量と線路定数の過去問題も解説しています。
ケーブルの作用静電容量
3心のケーブル各導体間の静電容量を Cm 、各導体と対地間の静電容量を Cs とすると図(a)のように表すことができます。鉛被の電位は 0 電位で等しいので、図(b)のように表わされます。
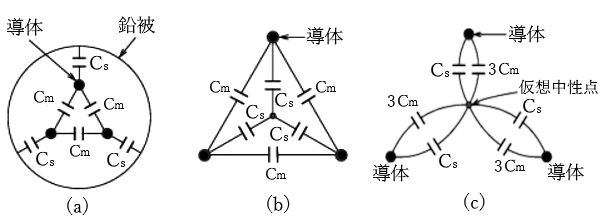
導体の仮想中性点の電位と鉛被の電位は0電位で等しいので、線間静電容量 Cm を△→Y変換すると、図(c)のように 3Cm と対地静電容量 CS は並列になり、1線当たりの静電容量は次の式で求めることができます。
ケーブルの1線当たりの静電容量を求める式
$C_n=3C_m+C_S$
$C_n$[F]:1線当たりの静電容量
$C_m$[F]:3心のケーブル各導体間の静電容量
$C_s$[F]:各導体と対地間の静電容量


ケーブルの1線当たりの静電容量 Cn を作用静電容量といいます。一般的に、三相電力ケーブルの作用静電容量は、図(d)の等価回路で表されます。
ここで、相電圧を E[V]線間電圧を V[V]、1線当たりのケーブルの充電電流を IC[A] とすると、次の関係式が成り立ちます。
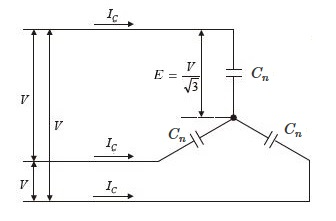
$E=\displaystyle \frac{ I_C }{ ωC_n }$[V]
$\begin{eqnarray}I_C&=&ωC_nE\\\\&=&ωC_n\displaystyle \frac{ V }{ \sqrt{ 3 } }\\\\&=&2πfC_n\displaystyle \frac{ V }{ \sqrt{ 3 } }[A]\end{eqnarray}$
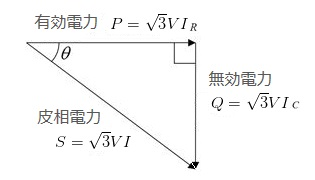
この電線全体のコンデンサ分に充電される電力は、無効電力として表すことができます。したがって、電線全体の充電容量 QC は次の式で求めることができます。
電圧 V、周波数 f、電線の作用静電容量 Cn のときの三相電線路の充電容量を求める式
$\begin{eqnarray}Q_C&=&\sqrt{ 3 }VI_C\\\\&=&\sqrt{ 3 }V×2πfC_n\displaystyle \frac{ V }{ \sqrt{ 3 } }\\\\&=&2πfC_nV^2[var]\end{eqnarray}$
$Q_C$ [var] : 電線全体の充電容量
$f$ [Hz] : 周波数
$C_n$ [F] : 電線1 線当たりの静電容量
$V$ : 線間電圧
送電線の線路定数
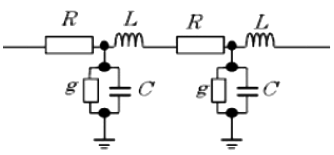
送電線の抵抗 R、作用インダクタンス L、作用静電容量 C 及び漏れコンダクタンス(リーカンス) g は、線路定数といい、電線路の電気的特性を表す値です。
線路定数は、電線の種類、電線の太さ、電線の構造、電線の幾何学的配置などによって定まる値であって、送電電圧、電流、力率、気象条件などによって線路定数の値が左右されることはなく、常に一定となります。
抵抗 R
送電線の抵抗 R[Ω]は、電線の長さに比例し、断面積に反比例します。導体の抵抗率を ρ[Ω⋅m]、長さを L[m]、断面積を S[m2]とすると、次の式で求めることができます。
電線の長さ、太さ、導体の抵抗率から抵抗を求める式
$R=ρ\displaystyle \frac{ L }{ S }$[Ω]
R[Ω]:抵抗
ρ[Ω⋅m]:導体の抵抗率
S[m2]:電線の断面積
L[m]:電線の長さ
作用インダクタンス L
コイルにはインダクタンスがあり、コイルに流れる電流によって自己誘導作用が起こります。同じように、電線にもインダクタンスがあり、電線に流れる電流により自己誘導作用が起こります。
三相3線式の送電線路には、自己インダクタンスと相互インダクタンスの2つがあり、電線1本のインダクタンスを自己インダクタンス、電線間のインダクタンスを相互インダクタンスといいます。また、この2つを合わせたものを「作用インダクタンス」といいます
単位長あたりの3線分のインダクタンス L3n[mH/km]は、電線の半径を r[m]、電線間の距離を D[m]、導体の比透磁率を μs とすると、次の式で求めることができます。
$L_{3n}=0.05μs+0.4605\log_{ 10 }\displaystyle \frac{ D }{ r }$[mH/km]
作用インダクタンスは、$\displaystyle \frac{ D }{ r }$ に比例
- 電線間の距離 D が大きくなると、作用インダクタンスは大きくなる。
- 電線の半径 r が大きくなる(電線が太くなる)と、作用インダクタンスは小さくなる。
作用静電容量 C
コンデンサには静電容量があり、電荷を蓄える能力があります。同じように、電線にも静電容量があり、電荷を蓄える能力があります。
三相3線式の送電線路には、対地静電容量と線間静電容量の2つがあり、電線1本と大地間の静電容量を対地静電容量、各電線間の静電容量を線間静電容量といいます。また、この2つを合わせたものを「作用静電容量」といいます
単位長あたりの3線分の静電容量 C3n[μF/km]は、電線の半径を r[m]、電線間の距離を D[m]、導体の比誘電率を εs とすると、次の式で求めることができます。
$C_{3n}=\displaystyle \frac{ 0.02413 εs}{ log_{ 10 } \displaystyle \frac{ D }{ r }}$[μF/km]
作用静電容量は、$\displaystyle \frac{ D }{ r }$ に反比例
- 電線間の距離 D が大きくなると、作用静電容量は小さくなる。
- 電線の半径 r が大きくなる(電線が太くなる)と、作用静電容量は大きくなる。
漏れコンダクタンス(リーカンス) g
漏れコンダクタンスは主に、がいし表面を流れる漏れ電流の抵抗の逆数のことです。がいし表面の抵抗はとても大きいので、これの逆数である漏れコンダクタンスは非常に小さい値になります。
1線の漏れコンダクタンスを g[S/km]、対地静電容量を C[F/km]、周波数を f[Hz]とすると、並列アドミタンス y[S/km]は、次の式で求めることができます。
$y=g+j2πfC$[S/km]
誘電体損
ケーブルやコンデンサの充電回路の等価回路は図のようになります。
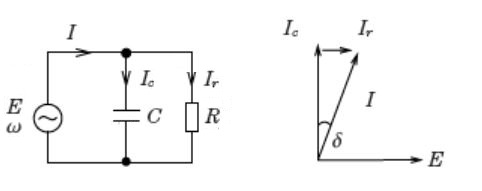
このとき、
$\displaystyle \frac{ I_r }{ I_C }=\displaystyle \frac{ 1 }{ ωCR }=tanδ$
$ I_r =I_Ctanδ$
の式が成り立ちます。この tanδ は誘電正接といい、δ(読み:デルタ)を誘電損角といいます。
誘電体に交流電界を加えたとき、誘電体内で電力の損失が起こります。これを誘電体損といいます。誘電体に交流電圧を加えたとき、電流は 90°より誘電損角 δ だけ小さくなります。ケーブルの作用静電容量を Cn[F/km]、相電圧を E[V]とすると、1相あたりの誘電体損 Wd[W]は、次の式で求めることができます。
三相電線路の誘電体損を求める式
$\begin{eqnarray}W_d&=&EI_r=E×I_Ctanδ\\\\&=&E×ωC_nEtanδ\\\\&=&2πfC_nE^2tanδ[W]\end{eqnarray}$
$W_d$[W]:誘電体損
$E$[V] : 相電圧
$C_n$[F]:電線1 線当たりの静電容量
$tanδ$:誘電正接
誘電体損はケーブルの発熱となり、許容電流を低下させます。尚、使用電圧11[kV]以下のケーブルでは通常、誘電体損は考慮しません。
電験三種-電力(送配電)過去問題
2003年(平成15年)問11
電圧 22[kV]、周波数 50[Hz]、こう長 1[km]の三相3線式地中電線路がある。ケーブルの心線1線当たりの静電容量が 0.44[μF/km]であるとき、この電線路の無負荷充電容量[kvar]の値として、最も近いのは次のうちどれか。
(1) 11 (2) 18 (3) 39 (4) 67 (5) 116
2003年(平成15年)問11 過去問解説
無負荷充電容量 QC とすると
$\begin{eqnarray}Q_C&=&2πfC_nV^2\\&=&2×3.14×50×0.44×10^{-6}×(22×10^3)^2\\&≒&66869[var]\end{eqnarray}$
答え (4)
2005年(平成17年)問8
架空送電線路の線路定数には、抵抗 R、作用インダクタンス L、作用静電容量 C 及び漏れコンダクタンス G がある。このうち、G は実用上無視できるほど小さい場合が多い。 R の値は電線断面積が大きくなると小さくなり、温度が高くなれば( ア )なる。また、一般に電線の交流抵抗値は直流抵抗値より( イ )なる。L と C は等価線間距離 D と電線半径 r の比( D/r )により大きく影響される。比( D/r )の値が大きくなれば、 L の値は( ウ )なり、C の値は( エ )なる。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に記入する語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 大きく | 大きく | 大きく | 小さく |
| (2) | 大きく | 小さく | 大きく | 大きく |
| (3) | 小さく | 大きく | 小さく | 小さく |
| (4) | 小さく | 大きく | 大きく | 小さく |
| (5) | 大きく | 大きく | 小さく | 大きく |
2005年(平成17年)問8 過去問解説
電線の抵抗 R は断面積に反比例し、温度に比例します。また、交流による表皮効果により直流抵抗より交流抵抗の方が大きくなります。
作用インダクタンス L、作用静電容量 C は、
$L=0.05μs+0.4605\log_{ 10 }\displaystyle \frac{ D }{ r }$[mH/km]
$C=\displaystyle \frac{ 0.02413 εs}{ log_{ 10 } \displaystyle \frac{ D }{ r }}$[μF/km]
で求めることができます。D/r が大きくなることは L は増加、C は減少します。
答え (1)
2009年(平成21年)問11
電圧 33[kV]、周波数 60[Hz]、こう長 2[km]の交流三相3線式地中配電線路がある。 ケーブルの心線一線あたりの静電容量が 0.24[μF/km]、誘電正接 0.03[%]であるとき、このケーブルの心線3線合計の誘電体損[W]の値として、最も近いのは次のうちどれか。
(1) 9.4 (2) 19.7 (3) 29.5 (4) 59.1 (5) 177
2009年(平成21年)問11 過去問解説
単位長あたりの作用静電容量を Cn[F/km]、相電圧を E[V]とすると、1相あたりの誘電体損 Wd[W/km]は、
$\begin{eqnarray}W_d&=&2πfC_nE^2tanδ\\\\&=&2π×60×0.24×10^{-6}×\left(\displaystyle \frac{ 33×10^3 }{ \sqrt{ 3 } }\right)^2×\displaystyle \frac{ 0.03 }{ 100 }\\\\&=&9.85[W/km]\end{eqnarray}$
こう長 2[km]で 3相分の誘電体損は、
$9.85×2×3=59.1$[W]
答え (4)
2012年(平成24年)問11
電圧 6.6 [kV] 、周波数 50 [Hz] 、こう長 1.5 [km] の交流三相3線式地中電線路がある。ケーブルの心線1線当たりの静電容量を 0.35 [μF/km] とするとき、このケーブルの心線3線を充電するために必要な容量 [kV・A] の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 4.2 (2) 4.8 (3) 7.2 (4) 12 (5) 37
2012年(平成24年)問11 過去問解説
充電容量 QC とすると
$\begin{eqnarray}Q_C&=&2πfC_nV^2\\\\&=&2×3.14×50×0.35×10^{-6}×1.5×(6.6×10^3)^2 \\\\&=& 7180[V・A] \end{eqnarray}$
答え (3)
2015年(平成27年)問10
電圧 66kV、周波数 50Hz、こう長 5kmの交流三相3線式地中電線路がある。ケーブルの心線1線当たりの静電容量が 0.43μF/km、誘電正接が 0.03%であるとき、このケーブル心線3線合計の誘電体損の値 [W] として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 141 (2) 294 (3) 883 (4) 1324 (5) 2648
2015年(平成27年)問10 過去問解説
単位長あたりの作用静電容量を Cn[F/km]、相電圧を E[V]とすると、1相あたりの誘電体損 Wd[W/km]は、
$\begin{eqnarray}W_d&=&2πfC_nE^2tanδ\\\\&=&2π×50×0.43×10^{-6}×\left(\displaystyle \frac{ 66×10^3 }{ \sqrt{ 3 } }\right)^2×\displaystyle \frac{ 0.03 }{ 100 }\\\\&=&58.84[W/km]\end{eqnarray}$
こう長 5[km]で 3相分の誘電体損は、
$58.84×5×3=882.6$[W]
答え (3)
2017年(平成29年)問16
図に示すように、対地静電容量 Ce[F]、線間静電容量 Cm[F]からなる定格電圧 E[V]の三相1回線のケーブルがある。
今、受電端を開放した状態で、送電端で三つの心線を一括してこれと大地間に定格電圧 E[V]の $\displaystyle \frac{ 1}{ \sqrt{ 3 } }$ 倍の交流電圧を加えて充電すると全充電電流は 90Aであった。
次に、二つの心線の受電端・送電端を接地し、受電端を開放した残りの心線と大地間に定格電圧 E[V]の $\displaystyle \frac{ 1}{ \sqrt{ 3 } }$ 倍の交流電圧を送電端に加えて充電するとこの心線に流れる充電電流は 45Aであった。
次の(a)及び(b)の問に答えよ。
ただし、ケーブルの鉛被は接地されているとする。また、各心線の抵抗とインダクタンスは無視するものとする。なお、定格電圧及び交流電圧の周波数は、一定の商用周波数とする。
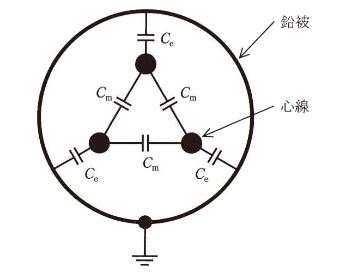
(a) 対地静電容量 Ce[F]と線間静電容量 Cm[F]の比 $\displaystyle \frac{ Ce}{ Cm }$ として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.5 (2) 1.0 (3) 1.5 (4) 2.0 (5) 4.0
(b) このケーブルの受電端を全て開放して定格の三相電圧を送電端に加えたときに 1線に流れる充電電流の値 [A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 52.5 (2) 75 (3) 105 (4) 120 (5) 135
2017年(平成29年)問16 過去問解説
(a) 3心のケーブル各導体間の静電容量を Cm 、各導体と対地間の静電容量を Ce とすると次の図のように表すことができます。
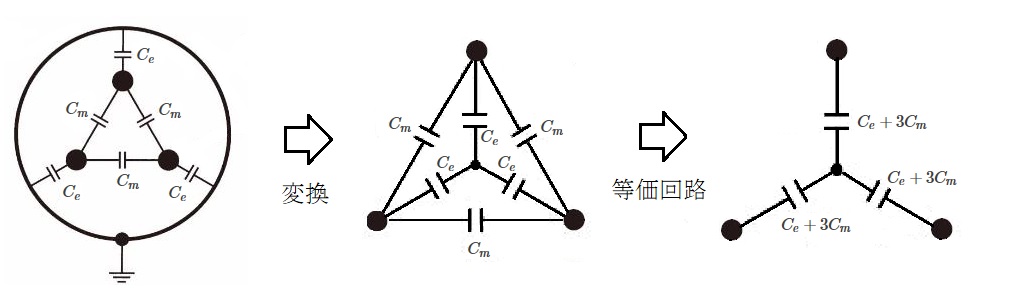
1線当たりの静電容量 Cn は次の式で求めることができます。
$Cn=3Cm+Ce$
$Cn$:1線当たりの静電容量[F]
三つの心線を一括した場合は、心線間は等電位となり、各導体間の静電容量 Cm はゼロになります。
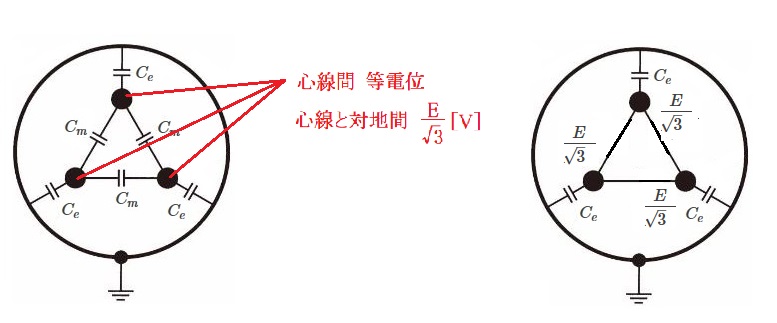
大地間に定格電圧 E[V]の $\displaystyle \frac{ 1}{ \sqrt{ 3 } }$ 倍の交流電圧を加えて充電したときの全充電電流を IC1[A]とすると、
$I_{C1}=ωCe×3×\displaystyle \frac{ E}{ \sqrt{ 3 } }=\sqrt{ 3 }ωCeE=90$[A]
$Ce=\displaystyle \frac{30\sqrt{ 3 } }{ ωE }$
二つの心線の受電端・送電端を接地し、受電端を開放した残りの心線に交流電圧を加えた場合、電位が 0 となった各導体間の対地静電容量 Ce と静電容量 Cm はゼロになります。

大地間に定格電圧 E[V]の $\displaystyle \frac{ 1}{ \sqrt{ 3 } }$ 倍の交流電圧を加えて充電したときの全充電電流を IC2[A]とすると、
$I_{C2}=ω(Ce+2Cm)×\displaystyle \frac{ E}{ \sqrt{ 3 } }=45$[A]
$Ce+2Cm=\displaystyle \frac{ 45\sqrt{ 3 } }{ ωE}$
$\displaystyle \frac{30\sqrt{ 3 } }{ ωE }+2Cm=\displaystyle \frac{ 45\sqrt{ 3 } }{ ωE}$
$Cm=\displaystyle \frac{ 15\sqrt{ 3 } }{ 2ωE}$
よって、$\displaystyle \frac{ Ce}{ Cm }$ は、
$\displaystyle \frac{ \displaystyle \frac{30\sqrt{ 3 } }{ ωE }}{ \displaystyle \frac{ 15\sqrt{ 3 } }{ 2ωE} }=4$
答え (5)
(b) 1線当たりの静電容量 Cn は、
$Cn=3Cm+Ce$
$Cn=3Cm+4Cm=7Cm={ \displaystyle \frac{ 105\sqrt{ 3 } }{ 2ωE} }$
充電電流を IC[A]とすると、
$I_C=ωC_nE=ωE×{ \displaystyle \frac{ 105\sqrt{ 3 } }{ 2ωE} }=52.5$[A]
答え (1)





