第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される単相交流の電力と力率について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された単相交流の電力と力率の過去問題も解説しています。
- 単相交流回路の電力と力率
- 交流電力のベクトル表示
- 交流電力の複素表示
- 電験三種-理論の過去問解説:単相交流の電力と力率
- 1998年(平成10年)問12【電験理論の過去問題】
- 2000年(平成12年)問12【電験理論の過去問題】
- 2001年(平成13年)問4【電験理論の過去問題】
- 2002年(平成14年)問6【電験理論の過去問題】
- 2004年(平成16年)問7【電験理論の過去問題】
- 2005年(平成17年)問16【電験理論の過去問題】
- 2007年(平成19年)問8【電験理論の過去問題】
- 2008年(平成20年)問9【電験理論の過去問題】
- 2010年(平成22年)問7【電験理論の過去問題】
- 2010年(平成22年)問8【電験理論の過去問題】
- 2011年(平成23年)問8【電験理論の過去問題】
- 2012年(平成24年)問8【電験理論の過去問題】
- 2014年(平成26年)問8【電験理論の過去問題】
- 2014年(平成26年)問10【電験理論の過去問題】
- 2014年(平成26年)問15【電験理論の過去問題】
- 2015年(平成27年)問8【電験理論の過去問題】
単相交流回路の電力と力率
単相の交流回路で、電源電圧 $e$[V]と電流 $i$[A]が次の式で与えられたとします。
$e=\sqrt{2}Esinωt$[V]
$i=\sqrt{2}Isin(ωt-θ)$[A]
この回路の瞬間消費電力 $p$[W]は、電源電圧 $e$[V]と電流 $i$[A]の積で求めることができます。
$\begin{eqnarray}p=ei&=&\sqrt{2}Esinωt・\sqrt{2}Isin(ωt-θ)\\&=&EIcosθ-EIcos(2ωt-θ)[W]\end{eqnarray}$
この式をグラフに描くと、次のようになります。
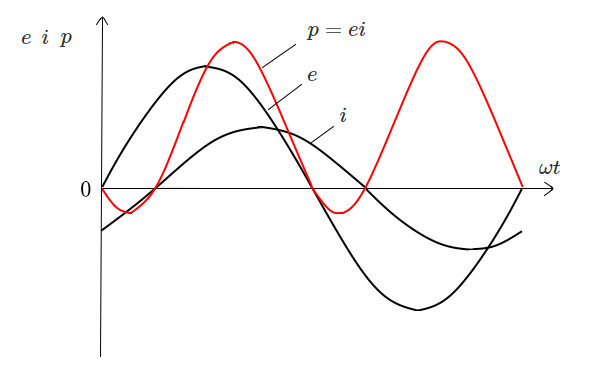
交流回路では、$p$[W]の平均値を電力 $P$[W]と考えます。$p=EIcosθ-EIcos(2ωt-θ)$ の、$EIcosθ$ は、時間に無関係です。つまり平均電力を表します。$EIcos(2ωt-θ)$ は、電源電圧の2倍の周波数を持ち、これを1周期にわたって平均すると $0$ になります。したがって、電力 $P$[W]は、次の式で表すことができます。
交流電力の公式
$P=EIcosθ$[W]
$E$[V]: 電圧の実効値
$I$[A]:電流の実効値
$cosθ$:電圧と電流の位相差
尚、$cosθ$ のことを「力率」といいます。力率は負荷のインピーダンス $Z$[Ω]に対する、抵抗 $R$[Ω]の比で表すことができます。
$cosθ=\displaystyle \frac{R}{Z}$
交流電力のベクトル表示
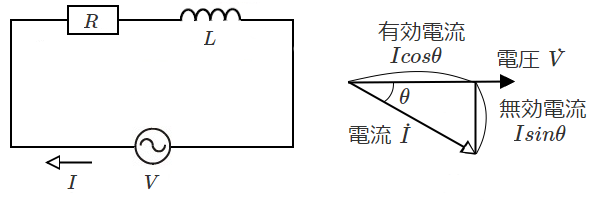
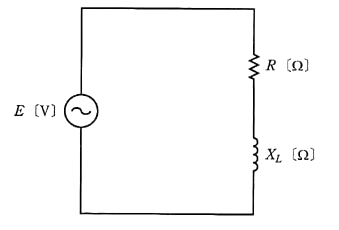
図のような $RL$ 直列回路では、電圧 $\dot{V}$[V]を加えると、電流 $\dot{I}$[A]が流れます。電流 $\dot{I}$ は、電圧 $\dot{V}$ より $θ$ 遅れます。
電流 $\dot{I}$ は、電圧 $\dot{V}$ と同相の $Icosθ$ の有効電流と電圧 $\dot{V}$ より $90°$遅れた $Isinθ$ の無効電流に分けることができます。この有効電流と無効電流に電圧 $V$ を掛けた値は、それぞれ電力を表します。
交流電力には、皮相電力 $S$[V・A]、有効電力 $P$[W]、無効電力 $Q$[var]があり、次のように表すことができます。
皮相電力、有効電力、無効電力の公式
皮相電力:$S=VI=I^2Z$[V・A]
有効電力:$P=VIcosθ=I^2R$[W]
無効電力:$Q=VIsinθ=I^2X_L$[var]
$S=\sqrt{P^2+Q^2}$
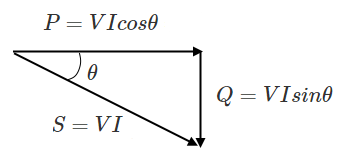
交流電力の複素表示
交流回路の電圧と電流は、次のように複素数で表すことができます。
$\dot{V}=a+jb$[V]
$\dot{I}=c+jd$[A]
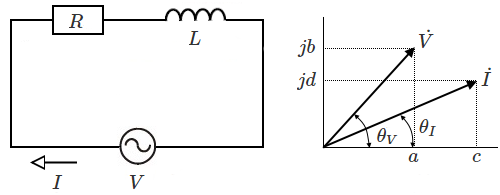
電圧 $\dot{V}$[V]と電流 $\dot{I}$[A]は、図のように $θ_V$,$θ_I$ の位相を持ちます。電圧 $\dot{V}$ と電流 $\dot{I}$ の積で皮相電力を求めたい場合は、共役複素数を使って計算します。
共役複素数とは、複素数 $z=a+bi$ に対して $\overline{ z}=a−bi$ のことをいいます。複素数 $z$ の共役をとるということは、虚部の $±$ の符号を変えるということです。複素平面上では、実軸に関する対称移動に対応しています。
電流を共役複素数として計算すると、遅れ無効電力が正符号として示され、電圧を共役複素数として計算すると、遅れ無効電力が負符号として示されます。
$\dot{V}\overline{\dot{I}}=(a+jb)(c-jd)=ac+bd+j(bc-ad)$
または
$\overline{\dot{V}}\dot{I}=(a-jb)(c+jd)=ac+bd+j(ad-bc)$
電験三種-理論の過去問解説:単相交流の電力と力率
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1998年(平成10年)問12【電験理論の過去問題】
図のような交流回路において、電圧 $\dot{V}$[V]及び電流 $\dot{I}$[A]が次の式で表されるとき、抵抗 $R$ で消費される電力 $P$[W]及びこの回路力率 $cosθ$ の値として、正しいものを組み合わせたのは次のうちどれか。
$\dot{V}=3+j4$
$\dot{I}=4+j3$[A]
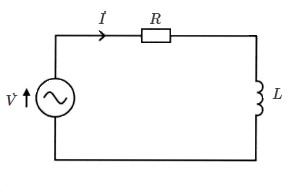
(1) $P=12$ $cosθ=0.75$
(2) $P=12$ $cosθ=0.87$
(3) $P=12$ $cosθ=0.96$
(4) $P=24$ $cosθ=0.87$
(5) $P=24$ $cosθ=0.96$
複素電力 $\dot{V}\overline{\dot{I}}$[V・A]は、
$\dot{V}\overline{\dot{I}}=(3+j4)(4-j3)=24+j7$[V・A]
したがって、有効分は24[KW]になります。力率 $cosθ$ は、
$cosθ=\displaystyle \frac{24}{\sqrt{24^2+7^2}}=\displaystyle \frac{24}{25}=0.96$
答え (5)
2000年(平成12年)問12【電験理論の過去問題】
図のような回路において、電力を測定したところ、電力計の指示は、320[W]であった。この場合の(a)及び(b)に答えよ。
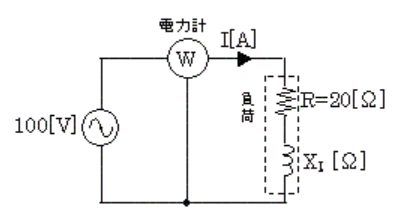
(a) 負荷電流 I[A]の値として、正しいのは次のうちどれか。
(1) 1 (2) 2 (3) 3 (4) 4 (5) 5
(b) 負荷の誘導リアクタンス XL の大きさの値として、正しいのは次のうちどれか。
(1) 15 (2) 20 (3) 25 (4) 30 (5) 35
(a) 電力計Wの指示Pは、抵抗 R=20[Ω]で消費される電力です。
$P=I^2R$[W]
$I=\sqrt{\displaystyle \frac{P}{R}}= \sqrt{\displaystyle \frac{320}{20}}=\sqrt{16}=4$ [A]
答え (4)
(b) 回路のインピーダンス $Z$ は、
$Z=\displaystyle \frac {V}{I}=\displaystyle \frac {100}{4} =25$ [Ω]
$R^2+{X_L}^2=Z^2$ なので、
${X_L}^2=25^2-20^2=225$
$X_L =15$[Ω]
答え (1)
2001年(平成13年)問4【電験理論の過去問題】
図の交流回路のおいて、抵抗 $R_2$ で消費される電力[W]として、正しいのは次のうちどれか。
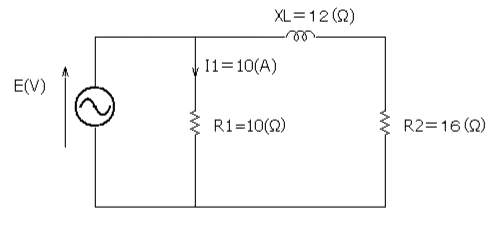
(1) 80 (2) 200 (3) 400 (4) 600 (5) 1000
電源電圧の大きさ $E$[V]は、
$E=I_1R_1=10×10=100$[V]
抵抗 $R_2$ に流れる電流の大きさを $I_2$[A]とすると、
$\begin{eqnarray}I_2&=&\displaystyle \frac{E}{\sqrt{{R_2}^2+{X_L}^2}}\\\\&=&\displaystyle \frac{100}{\sqrt{16^2+12^2}}\\\\&=&\displaystyle \frac{100}{\sqrt{400}}=5[A]\end{eqnarray}$
抵抗 $R_2$ で消費される電力 $P_2$[W]は、
$P_2={I_2}^2R=5^2×16=400$[W]
答え (3)
2002年(平成14年)問6【電験理論の過去問題】
図のように、抵抗 $R$[Ω]と誘導性リアクタンス $X_L$[Ω]が直列に接続された交流回路がある。$\displaystyle \frac{ R }{ X_L }=\displaystyle \frac{ 1 }{ \sqrt{2} }$ の関係があるとき、この回路の力率 $cosθ$ の値として、最も近いのは次のうちどれか。
(1) 0.43 (2) 0.50 (3) 0.58 (4) 0.71 (5) 0.87
力率は、$cosθ=\displaystyle \frac{R}{Z}$ で求めることができます。題意より、$ X_L = \sqrt{2}R$ なので、
$\begin{eqnarray}cosθ&=&\displaystyle \frac{R}{\sqrt{R^2+{X_L}^2}}\\\\&=&\displaystyle \frac{R}{\sqrt{R^2+( \sqrt{2}R)^2}}\\\\&=&\displaystyle \frac{R}{\sqrt{ 3R^2}}\\\\&=&\displaystyle \frac{1}{ \sqrt{3}}≒0.58 \end{eqnarray}$
答え (3)
2004年(平成16年)問7【電験理論の過去問題】
図のような $RC$ 交流回路がある。この回路に正弦波交流電源 $E$[V]を加えたとき、容量性リアクタンス $6$[Ω]のコンデンサの端子間電圧の大きさは $12$[V]であった。このとき、$E$[V]と図の破線で囲んだ回路で消費される電力 $P$[W]の値として、正しいものを組み合わせたのは次のうちどれか。
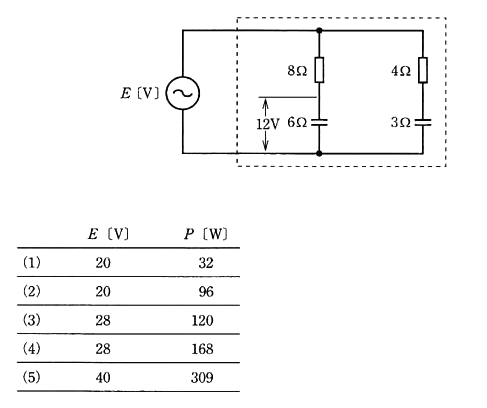
容量性リアクタンス $6$[Ω]のコンデンサに流れる電流は、$\displaystyle \frac{12}{6}=2$[A]なので、$8$[Ω]の抵抗の両端電圧は、$8×2=16$[V]になります。したがって、電源電圧の大きさ $E$[V]は、
$E=\sqrt{16^2+12^2}=20$[V]
$4$[Ω]の抵抗と容量性リアクタンス $3$[Ω]のコンデンサの合成インピーダンスは、$\sqrt{4^2+3^2}=5$[Ω]なので、流れる電流の大きさは $\displaystyle \frac{20}{5}=4$[A]になります。したがって $P$[W]は、
$P=2^2×8+4^2×4=32+64=96$[W]
答え (2)
2005年(平成17年)問16【電験理論の過去問題】
図の交流回路において、回路素子は、インダクタンス $L$ のコイル又は静電容量 $C$ のコンデンサである。この回路に正弦波交流電圧 $v=500sin(1000t)$[V]を加えたとき、回路に流れる電流は $i=-50cos(1000t)$[A]であった。このとき、次の(a)及び(b)に答えよ。
(a) 回路素子の値として、正しいのは次のうちどれか。
(1) $C=100$[nF]
(2) $L=10$[mH]
(3) $L=100$[mH]
(4) $C=10$[nF]
(5) $C=10$[μF]
(b) この回路素子に蓄えられるエネルギーの最大値 $W_{max}$[J]の値として、正しいのは次のうちどれか。
ただし、インダクタンスの場合には $\displaystyle \frac{ 1 }{ 2 }Li^2$ の、静電容量の場合には $\displaystyle \frac{ 1 }{ 2 }CV^2$ のエネルギーが蓄えられるものとする。
(1) 125 (2) 25 (3) 12.5 (4) 6.25 (5) 2.5
(a) $i=-50cos(1000t)$[A]を変形すると、
$\begin{eqnarray}i&=&-50cos(1000t)\\\\&=&-50sin(\displaystyle \frac{ π }{ 2 }-1000t)\\\\&=&50sin(1000t-\displaystyle \frac{ π }{ 2 })[A]\end{eqnarray}$
電流波形は電圧波形より90°遅れていますので、回路素子はリアクタンスになります。したがって、
$X_L=ωL=\displaystyle \frac{ 500 }{ 50}=10$[Ω]
$L=\displaystyle \frac{ 10 }{ ω}=\displaystyle \frac{ 10 }{ 1000}=10$[mH]
答え (2)
(b) $W_{max}$ は、題意より
$\begin{eqnarray}W_{max}&=&\displaystyle \frac{ 1 }{ 2 }Li^2\\\\&=&\displaystyle \frac{ 1 }{2}×10×10^{-3}×50^2\\\\&=&12.5[J]\end{eqnarray}$
答え (3)
2007年(平成19年)問8【電験理論の過去問題】
図のように、$8$[Ω]の抵抗と静電容量 $C$[F]のコンデンサを直列に接続した交流回路がある。この回路において、電源 $E$[V]の周波数を $50$[Hz]にしたときの回路の力率は、$80$[%]になる。電源 $E$[V]の周波数を $25$[Hz]にしたときの回路の力率[%]の値として、最も近いのは次のうちどれか。
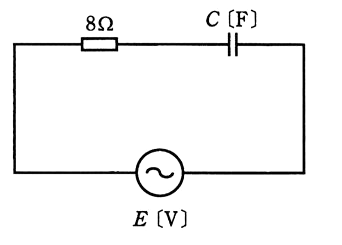
(1) 40 (2) 42 (3) 56 (4) 60 (5) 83
周波数 $50$[Hz]のときの容量性リアクタンスを $X_C$[Ω]とすると、力率は $80$[%]ですので、
$cosθ=\displaystyle \frac{ 8 }{ 8^2+{X_C}^2 }=0.8$
$8^2+{X_C}^2=100$
${X_C}=\sqrt{100^2-64^2}=6$
周波数 $25$[Hz]のときの容量性リアクタンスを $X_C’$[Ω]とすると、容量性リアクタンスは、$\displaystyle \frac{ 1 }{ ωC }$[Ω]ですので、
$25X_C’=50X_C=50×6$[Ω]
$X_C’=12$[Ω]
周波数を $25$[Hz]のときの力率を $cosθ’$ とすると、
$cosθ’=\displaystyle \frac{ 8 }{ 8^2+12^2 }≒0.555$
最も近いのは 56[%]となります。
答え (3)
2008年(平成20年)問9【電験理論の過去問題】
図のように、周波数 $f$[Hz]の交流電圧 $E$[V]の電源に、$R$[Ω]の抵抗、インダクタ ンス $L$[H]のコイルとスイッチSを接続した回路がある。スイッチSが開いているときに回路が消費する電力[W]は、スイッチSが閉じているときに回路が消費する電力[W]の $\displaystyle \frac{1}{2}$ になった。このとき、$L$[H]の値を表す式として、正しいものは次のうちどれか。
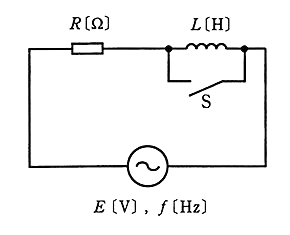
(1) $2πfR$ (2) $\displaystyle \frac{R}{2πf}$ (3) $\displaystyle \frac{2πf}{R}$ (4) $\displaystyle \frac{(2πf)^2}{R}$ (5) $(2πf)^2R$
スイッチSが開いているときに回路に流れる電流の大きさを $I_1$[A]、消費する電力を $P_1$[W]とすると、
$I_1=\displaystyle \frac{E}{\sqrt{R^2+(2πfL)^2}}$[A]
$\begin{eqnarray}P_1&=&I_1^2R\\\\&=&\left(\displaystyle \frac{E}{\sqrt{R^2+(2πfL)^2}}\right)^2R\\\\&=&\displaystyle \frac{E^2R}{R^2+(2πfL)^2}[W]\end{eqnarray}$
スイッチSが閉じているときに消費する電力を $P_2$[W]とすると、
$P_2=\displaystyle \frac{E^2}{R}$[W]
題意より
$P_1=\displaystyle \frac{1}{2}P_2$
$\displaystyle \frac{E^2R}{R^2+(2πfL)^2}=\displaystyle \frac{E^2}{2R}$
$2R^2=R^2+(2πfL)^2$
$L=\displaystyle \frac{R}{2πf}$
答え (2)
2010年(平成22年)問7【電験理論の過去問題】
抵抗 $R=4$[Ω]と誘導性リアクタンス $X=3$[Ω]が直列に接続された負荷を、図のように線間電圧 $\dot{V_ab} =100∠0°$[V],$\dot{V_bc} =100∠0°$[V]の単相 3 線式電源に接続した。このとき、これらの負荷で消費される総電力 $P$[W]の値として、正しいのは次のうちどれか。
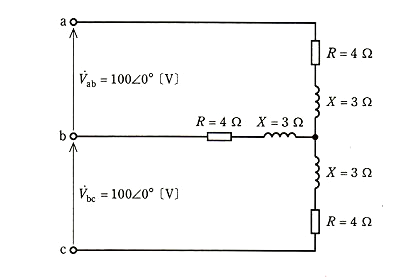
(1) 800 (2) 1200 (3) 3200 (4) 3600 (5) 4800
問の回路は単相3線式で、負荷が平衡しています。したがって、中性線には電流が流れません。問の回路を単相分の等価回路で考えます。
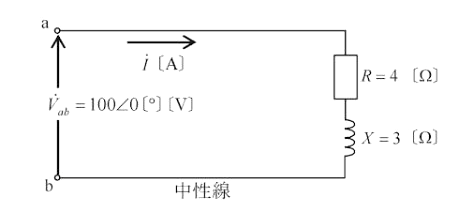
上図に流れる電流を $\dot{I}$[A]は、
$\dot{I}=\displaystyle \frac{100}{4+j3}=\displaystyle \frac{100(4-j3)}{(4+j3)(4-j3)}=16-j12$
電流の大きさ $I$[A]は、
$I=\sqrt{16^2+12^2}=20$[A]
単相分の消費電力 $P$[W]は、
$P=RI^2=4×20^2=1600$[W]
単相3線式ですので、$1600$[W]の2倍になります。
答え (3)
2010年(平成22年)問8【電験理論の過去問題】
抵抗 $R$[Ω]と誘導性リアクタンス $X_L$[Ω]を直列に接続した回路の力率($cosθ$)は、$\displaystyle \frac{1}{2}$ であった。いま、この回路に容量性リアクタンス $X_C$[Ω]を直列に接続したところ、$R$[Ω],$X_L$[Ω],$X_C$[Ω]直列回路の力率は、$\displaystyle \frac{\sqrt{3}}{2}$(遅れ)になった。容量性リアクタンス $X_C$[Ω]の値を表す式として、正しいのは次のうちどれか。
(1) $\displaystyle \frac{R}{\sqrt{3}}$ (2) $\displaystyle \frac{2R}{3}$ (3) $\displaystyle \frac{\sqrt{3}R}{2}$ (4) $\displaystyle \frac{2R}{\sqrt{3}}$ (5) $\sqrt{3}R$
抵抗 $R$[Ω]と誘導性リアクタンス $X_L$[Ω]を直列に接続した回路の力率 $cosθ$ は、
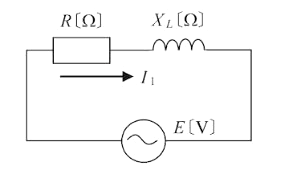
$cosθ=\displaystyle \frac{R}{\sqrt{R^2+{X_L}^2}}=\displaystyle \frac{1}{2}$
$2R=\sqrt{R^2+{X_L}^2}$
$X_L=\sqrt{3}R$
$R$[Ω]、$X_L$[Ω]、$X_C$[Ω]直列回路の力率 $cosθ’$ は
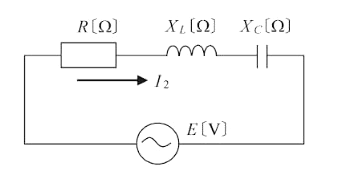
$cosθ’=\displaystyle \frac{R}{\sqrt{R^2+(X_L-X_C)^2}}=\displaystyle \frac{\sqrt{3}}{2}$
$X_L=\sqrt{3}R$ を代入すると、
$\displaystyle \frac{R}{\sqrt{R^2+(\sqrt{3}R-X_C)^2}}=\displaystyle \frac{\sqrt{3}}{2}$
$2R=\sqrt{3}×\sqrt{R^2+(\sqrt{3}R-X_C)^2}$
$4R^2=3R^2+3(\sqrt{3}R-X_C)^2$
$X_C=\displaystyle \frac{2R}{\sqrt{3}}$
答え (4)
2011年(平成23年)問8【電験理論の過去問題】
図の交流回路において、電源電圧を $\dot{E}=140∠0°$[V]とする。いま、この電源に力率 $0.6$ の誘導性負荷を接続したところ、電源から流れ出る電流の大きさは $37.5$[A]であった。次に、スイッチSを閉じ、この誘導性負荷と並列に抵抗 $R$[Ω]を接続したところ、電源から流れ出る電流の大きさが $50$[A]となった。このとき、抵抗 $R$[Ω]の大きさとして、正しいものを次の(1)~(5)のうちから一つ選べ.
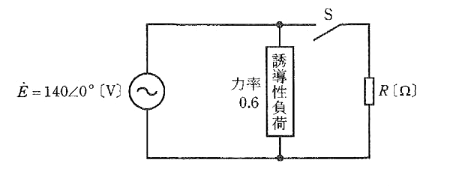
(1) 3.9 (2) 5.6 (3) 8.0 (4) 9.6 (5) 11.2
スイッチを開いているときに誘導性負荷に流れる電流を $\dot{I}_L$[A]とすると、
$\begin{eqnarray}\dot{I}_L&=&37.5(cosθ-jsinθ)\\\\&=&37.5(0.6-j0.8)=22.5-j30[A]\end{eqnarray}$
スイッチを閉じたときに抵抗に流れる電流を $\dot{I}_R$[A]とすると、
$\dot{I}_R+\dot{I}_L=\dot{I}_R+22.5-j30=50$
電流の大きさを $I_R$[A]は、
$\sqrt{(I_R+22.5)^2+30^2}=50$
$(I_R+22.5)^2+30^2=50^2$
$(I_R+22.5)^2=40^2$
$(I_R+22.5)=40$
$I_R=17.5$[A]
したがって、抵抗 $R$[Ω]は
$R=\displaystyle \frac{140}{17.5}=8.0$
答え (3)
2012年(平成24年)問8【電験理論の過去問題】
図のように、正弦波交流電圧 $E=200$[V]の電源がインダクタンス $L$[H]のコイルと $R$[Ω]の抵抗との直列回路に電力を供給している。回路を流れる電流が $I=10$[A]、回路の無効電力が $Q=1200$[var] のとき、抵抗 $R$[Ω]の値として、正しいものを次の(1)~(5)のうちから一つ選べ。
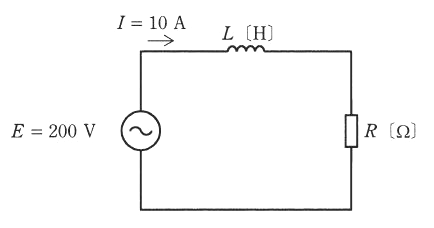
(1) 4 (2) 8 (3) 12 (4) 16 (5) 20
回路の皮相電力を $S$[V・A]、有効電力を $P$[W]とすると、
$S=EI=200×10=2000$[V・A]
$\begin{eqnarray}P&=&\sqrt{P^2-Q^2}\\\\&=&\sqrt{2000^2-1200^2}=1600\\\\&=&I^2R[W]\end{eqnarray}$
したがって抵抗 $R$[Ω]は、
$R=\displaystyle \frac{1600}{10^2}=16$[Ω]
答え (4)
2014年(平成26年)問8【電験理論の過去問題】
図の交流回路において、電源を流れる電流 $I$[A]の大きさが最小となるように静電容量 $C$[F]の値を調整した。このときの回路の力率の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
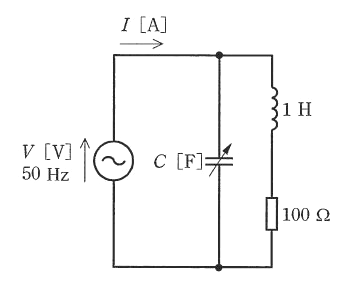
(1) 0.11 (2) 0.50 (3) 0.71 (4) 0.87 (5) 1
コンデンサに流れる電流を $\dot{I_C}$[A]、抵抗とコイルに流れる電流を $\dot{I}_{RL}$[A]とすると、
$\dot{I}_C=jωCV$[A]
$\begin{eqnarray}\dot{I}_{RL}&=&\displaystyle \frac{V}{R+jωL}\\\\&=&\displaystyle \frac{V(R-jωL)}{(R+jωL)(R-jωL)}\\\\&=&\displaystyle \frac{V(R-jωL)}{R^2+(ωL)^2}[A]\end{eqnarray}$
電源を流れる電流 $\dot{I}$[A]は、
$\begin{eqnarray}\dot{I}&=&\dot{I}_C+\dot{I}_{RL}\\\\&=&jωCV+\displaystyle \frac{V(R-jωL)}{R^2+(ωL)^2}\\\\&=&\left( \displaystyle \frac{R}{R^2+(ωL)^2}+jω\left( C-\displaystyle \frac{L}{R^2+(ωL)^2} \right) \right)×V[A]\end{eqnarray}$
電流 $\dot{I}$[A]を最小にする条件は、虚数部分が $0$ になるときです。したがって、電流 $I$[A]の大きさは実数部分だけになりますので、有効電流のみ流れます。有効電流のみということは、力率は $1$ になります。
答え (5)
2014年(平成26年)問10【電験理論の過去問題】
交流回路に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし、抵抗 $R$[Ω],インダクタンス $L$[H],静電容量 $C$[F]とする。
- 正弦波交流起電力の最大値を $E_m$[V]、平均値を $E_a$[V]とすると、平均値と最大値の関係は、理論的に次のように表される。
$E_a=\displaystyle \frac{2E_m}{π}≒0.637E_m[V]$ - ある交流起電力の時刻 $t$[s]における瞬時値が、$e=100sin100πt $[V]であるとすると、この起電力の周期は $20ms$ である。
- $RLC$ 直列回路に角周波数 $ω$[rad/s]の交流電圧を加えたとき、$ωL>\displaystyle \frac{1}{ωC}$の場合、回路を流れる電流の位相は回路に加えた電圧より遅れ、 $ωL<\displaystyle \frac{1}{ωC}$ の場合、回路を流れる電流の位相は回路に加えた電圧より進む。
- $RLC$ 直列回路に角周波数 $ω$[rad/s] の交流電圧を加えたとき、$ωL=\displaystyle \frac{1}{ωC}$の場合、回路のインピーダンス $Z$ [Ω] は、$Z=R$[Ω]となり、回路に加えた電圧と電流は同相になる。この状態を回路が共振状態であるという。
- $RLC$ 直列回路のインピーダンス $Z$[Ω]、電力 $P$[W]及び皮相電力 $S $[V・A] を使って回路の力率 $cosθ$を表すと、$cosθ=\displaystyle \frac{R}{Z}$,$cosθ=\displaystyle \frac{S}{P}$ の関係がある。
- 正しい記述です。
- 正しい記述です。
$2πf=100πt$
$f=50$[Hz]
$T=\displaystyle \frac{1}{T}=\displaystyle \frac{1}{50}=0.02$[s] - 正しい記述です。
交流電圧を $\dot{V}$、回路を流れる電流を $\dot{I}$ とすると、
$\dot{I}=\displaystyle \frac{\dot{V}}{R+j(ωL-\displaystyle \frac{1}{ωC})}$
$ωL>\displaystyle \frac{1}{ωC}$の場合、回路を流れる電流の位相は回路に加えた電圧より遅れ、 $ωL<\displaystyle \frac{1}{ωC}$ の場合、回路を流れる電流の位相は回路に加えた電圧より進みます。 - 正しい記述です。
$ωL=\displaystyle \frac{1}{ωC}$の場合は、共振状態です。 - 誤った記述です。
$cosθ=\displaystyle \frac{有効電力}{皮相電力}=\displaystyle \frac{P}{S}$
答え (5)
2014年(平成26年)問15【電験理論の過去問題】
図のように、正弦波交流電圧 E [V] の電源が誘導性リアクタンス X [Ω] のコイルと抵抗 R [Ω] との並列回路に電力を供給している。この回路において、電流計の指示値は 12.5 A、電圧計の指示値は 300 V、電力計の指示値は 2250 Wであった。
ただし、電圧計、電流計及び電力計の損失はいずれも無視できるものとする。
次の(a)及び(b)の問に答えよ。
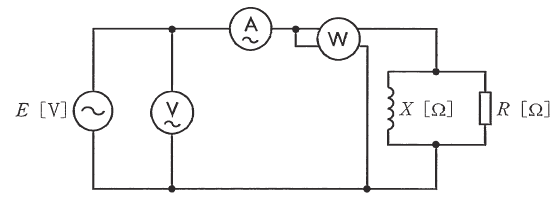
(a) この回路における無効電力 $Q$[var] として、最も近い $Q$ の値を次の(1)~(5)のうちから一つ選べ。
(1) 1800 (2) 2250 (3) 2750 (4) 3000 (5) 3750
(b) 誘導性リアクタンス $X$ [Ω] として、最も近い $X$ の値を次の(1)~(5)のうちから一つ選べ。
(1) 16 (2) 24 (3) 30 (4) 40 (5) 48
(a) 皮相電力を $S$[V・A]とすると
$S=300×12.5=3750$ [V・A]
有効電力を $P$[W]とすると、無効電力 $Q$[var]は、
$S=\sqrt{P^2+q^2}$
$Q=\sqrt{S^2-P^2}=\sqrt{3750^2-2250^2}=3000$[var]
答え (4)
(b) 力率 $cosθ$ 、インピーダンス $Z$ の値は、
$cosθ=\displaystyle\frac{P}{S}=\displaystyle\frac{2250}{3750}=0.6$
$Z=\displaystyle\frac{300}{12.5}=24$[Ω]
したがって、
$R=\displaystyle\frac{Z}{cosθ}=\displaystyle\frac{24}{0.6}=40$
$X=\displaystyle\frac{Z}{sinθ}=\displaystyle\frac{24}{0.8}=30$
答え (3)
2015年(平成27年)問8【電験理論の過去問題】
$R=10$[Ω]の抵抗と誘導性リアクタンス $X$[Ω]のコイルとを直列に接続し、$100$[V]の交流電源に接続した交流回路がある。いま、回路に流れる電流の値は $I=5$[A]であった。このとき、回路の有効電力 $P$ の値 [W]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 250 (2) 289 (3) 425 (4) 500 (5) 577
$P=I^2R=5^2×10=250$[W]
答え (1)






