第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される直流回路の重ね合わせの定理,ノートンの定理,テブナンの定理について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された直流回路の重ね合わせの定理,ノートンの定理,テブナンの定理の過去問題も解説しています。
定電圧源と定電流源
定電圧源とは負荷の大きさが変動しても、一定の電圧を供給できる電源のことです。定電流源とは負荷の大きさが変動しても、一定の電流を供給できる電源のことです。電源には必ず内部抵抗があるのですが、定電圧源と定電流源では、内部抵抗がどのようになっているのかを説明します。
定電圧源
電圧源とは、ある電源に抵抗を接続し、抵抗値を変化させたとしても、電源の端子電圧が一定で、電流が変化する電源のことです。
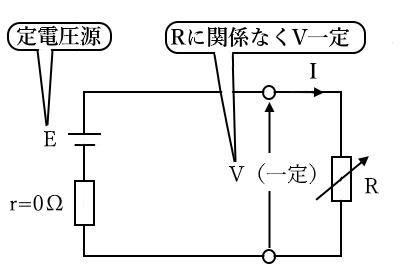
通常、電圧源は内部抵抗を持っています。図のように可変抵抗 $R$ に電流を流すと直列に接続されている内部抵抗 $r$ の電圧降下により端子電圧 $V$ は低下します。
もし内部抵抗が $r=0$ の理想的な電源なら、端子電圧 $V$ は可変抵抗 $R$ の値に関係なく一定の電圧を供給できます。つまり定電圧源とは、内部抵抗が $0$ の電圧源のことです。
定電流源
電流源とは、ある電源に抵抗を接続し、抵抗値を変化させたとしても、電源から流れ出る電流が一定で、電圧が変化する電源のことです。
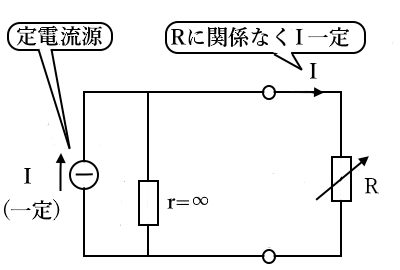
通常、電流源は内部抵抗を持っています。図のように可変抵抗 $R$ を接続すると、並列に接続されている内部抵抗 $r$ にも電流が流れ、可変抵抗 $R$ に流れる電流 $I$ は低下します。
もし内部抵抗が $r=∞$ の理想的な電源なら、内部抵抗 $r$ には電流が流れずに、可変抵抗 $R$ に流れる電流 $I$ は一定を保ちます。つまり電流源とは、内部抵抗が $∞$ の電流源のことです。
重ね合わせの理
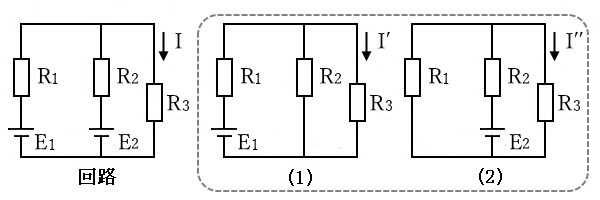
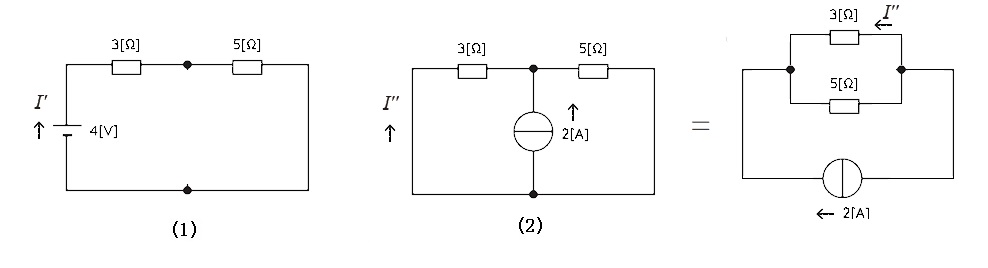
重ね合わせの理とは、電源が複数ある回路の電圧・電流は、電源が1個だけの回路に分解した電圧・電流の和に等しいというものです。
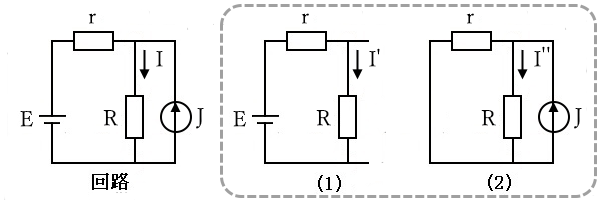
図の回路の $R_3$ に流れる電流 $I$ は、分解した(1)の回路の $R_3$ に流れる電流 $I’$ と(2)の回路の $R_3$ に流れる電流 $I”$ の和に等しいので
$I=I’+I”$
となります。電流源と電圧源が複数ある場合でも、重ね合わせの理は成立します。
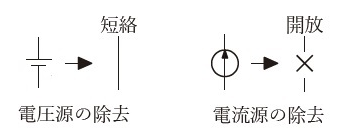
電圧源を除去する場合は回路を短絡します。電流源を除去する場合は回路を開放します。
テブナンの定理
テブナンの定理
電源を含んだ回路中の端子 ab 間に抵抗 $R$[Ω]を接続すると、抵抗 $R$ に流れる電流 $I$[A]は次の式で表すことができる。
$I=\displaystyle \frac{ V_0 }{ R_0+R }$
$V_0$:端子 ab 間を開放したときの端子間電圧
$R_0$:電圧源は短絡し、電流源は開放したときの、端子 ab から回路を見た合成抵抗
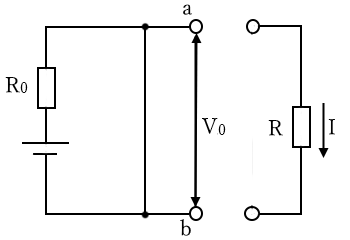
テブナンの定理は、等価定電圧源に対応します。
テブナンの定理 例題
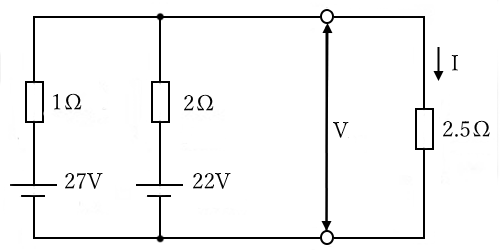
図の回路の端子電圧 $V$[V]の値を求めてみます。
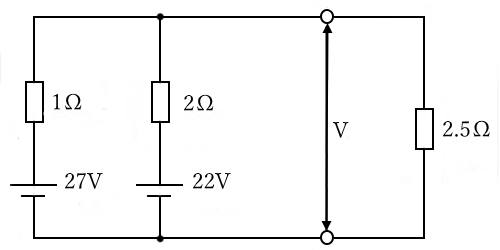
まずは次の図のように、2.5[Ω]の抵抗を開放したときの端子間電圧 $V_0$[V]を求めます。回路に流れる電流を $I’$[A]とすると、
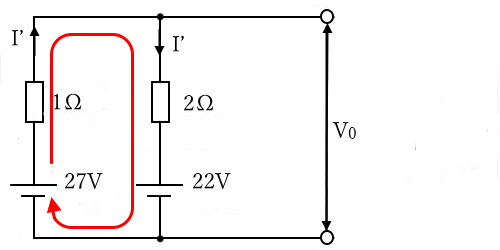
$I’=\displaystyle \frac{ 27-22 }{ 1+2 }=\displaystyle \frac{ 5 }{ 3 }$[A]
回路に流れる電流と抵抗から電圧降下を求めることができますので、$V_0$ は次のとおりになります。尚、27[V]と 22[V]のどちらの電源電圧で計算しても、同じ結果になります。
$V_0=27-1×\displaystyle \frac{ 5 }{ 3 }=\displaystyle \frac{ 76 }{ 3 }$[V]
$V_0=22+2×\displaystyle \frac{ 5 }{ 3 }=\displaystyle \frac{ 76 }{ 3 }$[V]
次に、電圧源を短絡し、開放した端子から見た合成抵抗 $R_0$ を計算します。
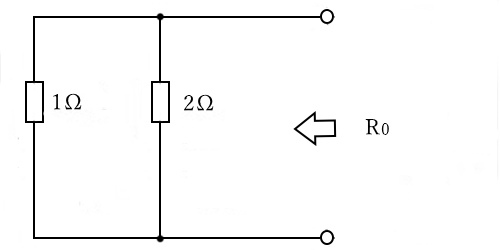
$R_0=\displaystyle \frac{ 1×2 }{ 1+2 }=\displaystyle \frac{ 2 }{ 3 }$[Ω]
テブナンの定理より、2.5[Ω]の抵抗に流れる電流 $I$[A]を求めることができます。
$I=\displaystyle \frac{ V_0 }{ R_0+R }=\displaystyle \frac{ \displaystyle \frac{ 76 }{ 3 } }{ \displaystyle \frac{ 2 }{ 3 }+2.5 }=\displaystyle \frac{ 76 }{ 9.5 }$[A]
求める電圧 $V$[V]は、
$V=2.5×I=2.5×\displaystyle \frac{ 76 }{ 9.5 }=20$[V]
電験三種-理論の過去問解説:回路計算の定理
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1997年(平成9年)問5【電験理論の過去問題】
図のような直流回路において、3[Ω]の抵抗を流れる電流[A]の値として、正しいのは次のうちどれか。

(1) 0.35 (2) 0.45 (3) 0.55 (4) 0.65 (5) 0.75
1999年(平成11年)問7【電験理論の過去問題】
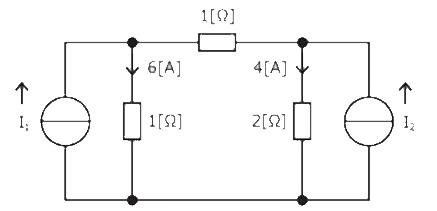
図の直流回路において、二つの電流源の電流 $I_1$[A]及び $I_2$[A]の値の組み合わせてして、正しい値は次のうちどれか。
(1) $I_1= 0$ $I_2=10$
(2) $I_1= 4$ $I_2=6$
(3) $I_1= 5$ $I_2=5$
(4) $I_1= 6$ $I_2=4$
(5) $I_1=10$ $I_2=0$
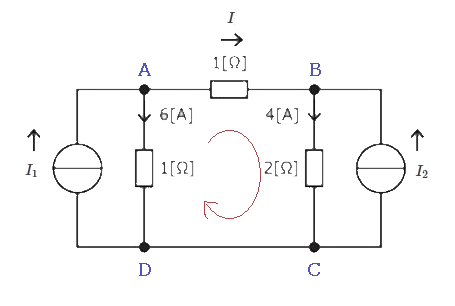
図のように 1[Ω]の抵抗に、左から右に流れる電流を $I$[A]とし、A点,B点にキルヒホッフの第1法則、A→B→C→Dループにキルヒホッフの第2法則を適用します。
$I_1=6+I$ … (1)
$I_2=4-I$ … (2)
$I+4×2-6×1=0$ … (3)
(1),(2),(3)を解くと、$I_1=4$,$I_2=6$
答え (2)
2006年(平成18年)問5【電験理論の過去問題】
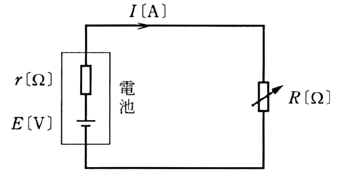
図のように内部抵抗 $r$[Ω]、起電力 $E$[V]の電池に抵抗 $R$[Ω]の可変抵抗器を接続した回路がある。$R=2.25$[Ω]にしたとき、回路を流れる電流 $I=3$[A]であった。つぎに、$R=3.45$[Ω]にしたとき、回路を流れる電流 $I=2$[A]となった。この電池の起電力 $E$[V]の値として、正しいのは次のうちどれか。
(1) 6.75 (2) 6.90 (3) 7.05 (4) 7.20 (5) 9.30
$R=2.25$[Ω]のときは
$E=3×(2.25+r)$ … (1)
$R=3.45$[Ω]のときは
$E=2×(3.45+r)$ … (2)
(1),(2)式より
$3×(2.25+r) =2×(3.45+r)$
$r=0.15$
$E=3×(2.25+0.15)=7.2$[V]
答え (4)
2012年(平成24年)問5【電験理論の過去問題】
図1のように電圧が $E$[V]の直流電圧源で構成される回路を、図2のように電流が $I$ [A]の直流電流源(内部抵抗が無限大で、負荷変動があっても定電流を流出する電源)で構成される等価回路に置き替えることを考える。この場合、電流 I[A]の大きさは図1の端子a-bを短絡したとき、そこを流れる電流の大きさに等しい。また、図2のコンダクタンス $G$[S]の大きさは図1の直流電圧源を短絡し、端子a-bからみたコンダクタンスの大きさに等しい。$I $[A]と $G$[S]の値を表す式の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
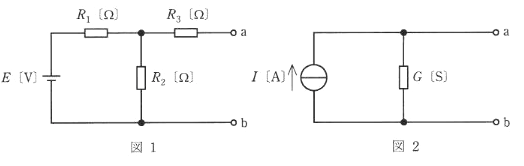

図1の端子a-bを短絡したときの合成抵抗を $R$ とすると、
$R=R_1+\displaystyle \frac{ R_2R_3 }{ R_2+R_3 }$
$R_1$に流れる電流を $I_1$ とすると、オームの法則より
$I_1=\displaystyle \frac{E}{R_1+\displaystyle \frac{ R_2R_3 }{ R_2+R_3 }}$
端子a-bに流れる電流 $I$ は、分流の法則より、
$\begin{eqnarray}I&=&\displaystyle \frac{ R_2}{ R_2+R_3 }×I_1\\\\&=&\displaystyle \frac{ R_2}{ R_2+R_3 }×\displaystyle \frac{E}{R_1+\displaystyle \frac{ R_2R_3 }{ R_2+R_3 }}\\\\&=&\displaystyle \frac{ R_2 }{ R_1R_2+R_1R_3+R_2R_3 }E\end{eqnarray}$
図2のコンダクタンス $G$[S]の大きさは図1の直流電圧源を短絡し、端子a-bからみたコンダクタンスの大きさに等しい。コンダクタンスは、端子 a-b からみた合成抵抗の逆数ですので、
$\begin{eqnarray}G&=&\displaystyle \frac{ 1}{\displaystyle \frac{ R_1R_2 }{ R_1+R_2 }+R_3}\\\\&=&\displaystyle \frac{ R_1+R_2 }{ R_1R_2+R_1R_3+R_2R_3 }E\end{eqnarray}$
答え (2)
電験三種の理論科目に出題される「直流分野」のページ
1.直流回路の基本問題
2.ホイートストンブリッジ回路
3.キルヒホッフの法則と不平衡ブリッジ
4.回路計算の定理(重ね合わせ・テブナン)
5.直流回路の消費電力