このページでは、パワーエレクトロニクス素子を使ったDC-DCコンバータを制御する直流チョッパについて、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の機械科目の試験で実際に出題された、直流チョッパ回路の原理についての過去問題も解説しています。
直流チョッパの基本
交流電力は変圧器を用いて、簡単に効率よく電圧変換ができますが、直流電力の電圧変換も半導体バルブデバイスを用いた直流チョッパによって取り扱いが容易で、効率のよい変換ができます。ここでは、直流チョッパの原理と利用例について解説します。
直流チョッパの転流回路
直流電力の制御は、交流電力の制御と同じように、サイリスタによって制御ができます。しかし、交流回路に使用されているサイリスタのアノード・カソード間の電源電圧は、半周期後には 0[V]になり、以後は逆電圧になります。したがって、アノード電流は遮断され、自然にターンオフしますが、直流回路に使用されているサイリスタのアノード・カソード間の電源電圧は、自然には 0[V]や逆電圧になりません。そのため、サイリスタをターンオフさせるための特別な回路が必要です。この回路を「転流回路」といいます。図1は転流回路の一例です。
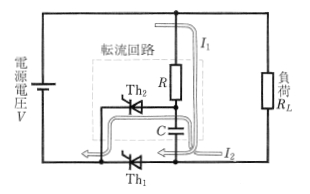
サイリスタ $Th_1$ がターンオンすると、コンデンサ $C$ には抵抗 $R$ を通じて、$I_1$[A]が流れ、電源電圧 $V$[V]まで充電されます。この状態で $Th_1$ をターンオフするためには、転流回路のサイリスタ $Th_2$ をターンオンさせます。すると、$C$ の電圧が $Th_2$ を通じて、$Th_1$ に逆電圧として加わり、一瞬にターンオフします。
$Th_1$ がオフになると、$C$ は電流 $I_2$[A]によって、以前とは逆の極性で $V$[V]まで充電されます。その後、$Th_1$ をターンオンさせると、$Th_2$ には $Th_1$ を通じて、$C$ の電圧が逆電圧として加わり、一瞬にターンオフし、もとの状態にもどります。このように一般のサイリスタは転流回路を必要とします。しかし、 3端子ターンオフサイリスタ(GTO)とよばれるサイリスタは転流回路を必要としません。GTOは、逆阻止3端子サイリスタと同じように、ゲートに正の電流を流すことによってターンオンしますが、ゲートに負の電流を流すことによって、容易にターンオフできる特徴をもっています。つまり、転流回路を必要としないため回路が簡単になり、広く利用されています。
直流チョッパの原理
図2(a)は直流チョッパの基本回路です。図(a)において、スイツチSの開閉を繰り返すと、負荷には断続した図(b)のような直流出力電圧が得られ、その出力電圧はスイッチのオンとオフの時間を変えることによって調整できます。これを「直流チョッパ」といいます。実際には、図(a)のように、スイッチSをサイリスタやトランジスタなどの半導体バルブデバイスに置き換え、電気信号を加えると、半導体バルブデバイスは高速のオンオフ動作ができ、効率もよく、細かな出力電圧の調整ができます。直流の出力電圧の調整は、図(b)のように、一定の周期 $T$[s]の中で、$T_{on}$[s]と $T_{off}$[s]の比を変えて行い、$T_{on}$[s]の割合が増えるに従って、平均出力電圧は点線のように増加していきます。
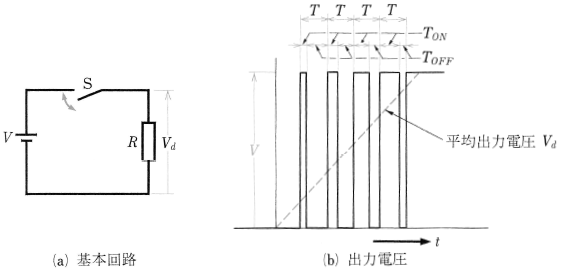
直流チョッパには、出力電圧が 0[V]から電源電圧まで変えられる「直流降圧チョッパ」、電源電圧以上に変えられる「直流昇圧チョッパ」、そして、この二つを組み合わせた「直流昇降圧チョッパ」とがあります。
直流降圧チョッパ
図3(a)はターンオフサイリスタ(GTO)を用いた直流降圧チョッパの回路です。抵抗 $R$[Ω]とインダクタンス $L$[H]をもった負荷と並列に、フリーホイーリングダイオード $D_F$ が接続されています。サイリスタを $T_{on}$[s]時間オン状態にすると、負荷には電源電流 $i_1$[A]が流れます。サイリスタを $T_{off}$[s]時間オフ状態にすると、$L$ に蓄えられたエネルギーが電流 $i_D$[A]となって、ダイオード $D_F$ を通り、負荷に還流します。このため、負荷電流 $i_d$図(b)に示すように、連続した脈動電流になります。
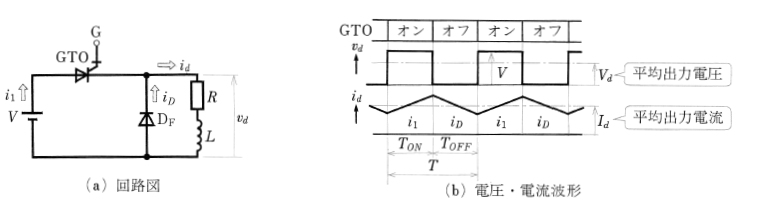
図(b)の周期 $T$[s]でオン・オフを繰り返すとき、出力電圧 $v_d$ の平均値、すなわち平均出力電圧 $V_d$[V]は次の式で表すことができます。
直流降圧チョッパ回路の平均出力電圧を求める式
$V_d=\displaystyle\frac{T_{on}}{T_{on}+T_{off}}V$
$V_d$[V]:平均出力電圧
$V$[V]:電源電圧
$T_{on}$:GTO がオンしている時間
$T_{off}$:GTO がオフしている時間
$\displaystyle\frac{T_{on}}{T_{on}+T_{off}}$ は、1より小さいので、平均出力電圧 $V_d$ は、電源電圧 $V$ より小さくなり、降圧します。
$T_{on}+T_{off}$ を「1周期」といい、$\displaystyle\frac{T_{on}}{T_{on}+T_{off}}$ を「通流率」といいます。通流率は $d$ で表し、1周期に対する $T_{on}$ の時間の割合を示します。
通流率を表す式
$d=\displaystyle\frac{T_{on}}{T_{on}+T_{off}}$
$d$:通流率
$T_{on}$:GTO がオンしている時間
$T_{off}$:GTO がオフしている時間
通流率が $d$ のときの直流降圧チョッパ回路の平均出力電圧を求める式
$V_d=dV$
$V_d$[V]:平均出力電圧
$d$:通流率
$V$[V]:電源電圧
直流昇圧チョッパ
図4は、トランジスタによる直流昇圧チョッパの回路です。 トランジスタ $Tr$ を $T_{on}$[s]時間オンにすると、インダクタンス $L$[H]に電流 $i_t$[A]が流れてエネルギーが蓄積されます。次に、$Tr$ を $T_{off}$[s]時間オフにすると、$L$[H]に蓄積されたエネルギーは電流 $i_d$ として放出され、ダイオード $D$ を通ってコンデンサ $C$[F]と負荷抵抗 $R$[Ω]に流れます。
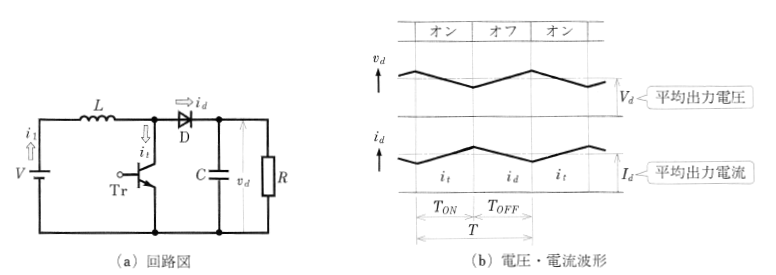
インダクタンス $L$[H]を十分に大きな値としたとき、平均出力電圧 $v_d$ の平均出力電圧を $V_d$[V]とすると、$VI_1T_{on}=(V_d-V)I_1T_{off}$ より $V_d$ は次のように表すことができます。
直流昇圧チョッパ回路の平均出力電圧を求める式
$V_d=\displaystyle\frac{T_{on}+T_{off}}{T_{off}}V$
$V_d$[V]:平均出力電圧
$V$[V]:電源電圧
$T_{on}$:トランジスタがオンしている時間
$T_{off}$:トランジスタがオフしている時間
$\displaystyle\frac{T_{on}+T_{off}}{T_{off}}V$ は、1より大きいので、平均出力電圧 $V_d$ は、電源電圧 $V$ より大きくなり、昇圧します。
通流率が $d$ のときの直流昇圧チョッパ回路の平均出力電圧を求める式
$V_d=\displaystyle\frac{1}{1-d}V$
$V_d$[V]:平均出力電圧
$d$:通流率
$V$[V]:電源電圧
直流チョッパの利用
直流チョッパの出力は効率よく、電圧制御ができるので、小・中容量の直流電源として、通信機器・電子機器・コンピュータ用電源などに用いられ、中・大容量の直流電源として、メッキ・アルミニウム精錬など電気化学用などに用いられています。
直流チョッパは、直流電動機の速度制御にも広く利用されています。電圧制御法の一つとして、直流チョッパを利用して、直流電動機の電機子電圧を変えて、回転速度を制御することができます。また、直流チョッパを用いて電動機の減速時には、電動機を発電機として動作させて、その電力を電源に回生して制動力を発生させ、あわせて省エネルギー化をはかることができます。
図5はその一例で、降圧形・昇圧形の二つのチョッパを組み合わせた「直流昇降圧チョッパ回路」であり、この電源装置の負荷に直流電動機Mが接続されています。
直流電動機の加速・駆動時には、図(a)の $Tr_2$をオフ状態に保って、$Tr_1$をオンオフ動作させます。回路は図(b)のようになり、図3の直流降圧チョッパ回路に一致します。そこで、$Tr_1$ のオン・オフの比率を変えて、電機子電流 $i_d$[A]が制御できます。
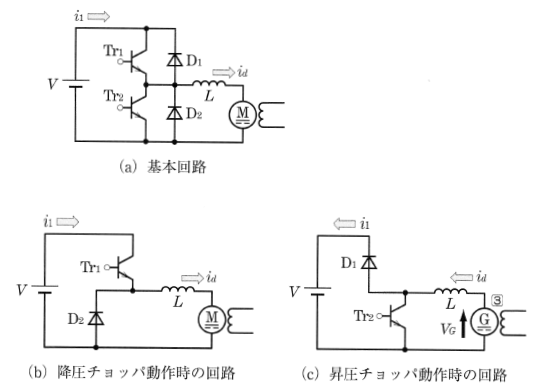
次に、減速時には、$Tr_1$をオフに保って、$Tr_2$ をオンオフ動作させると、回路は図(c)になり、図4の直流昇圧チョッパ回路に一致します。
直流電動機は、起電力 $V_G$[V]を発生する直流発電機として運転され、直流機側から昇圧チョッパを通って電源側に電流 $i_1$[A]が流れ、電力が電源に回生され、制動力が発生して減速します。
このような方法を電車の主電動機の制御に利用すると、電車が降圧チョッパで力行し、昇圧チョッパによって電力を電源に回生しながらブレーキ走行をすることができます。幹線鉄道・地下鉄などの電気鉄道の車両の主電動機や、電気自動車の電動機の電源装置に使用されています。
直流チョッパと同じように、小・中容量の直流電力を変換する電源装置としてスイッチングレギュレータが使われています。
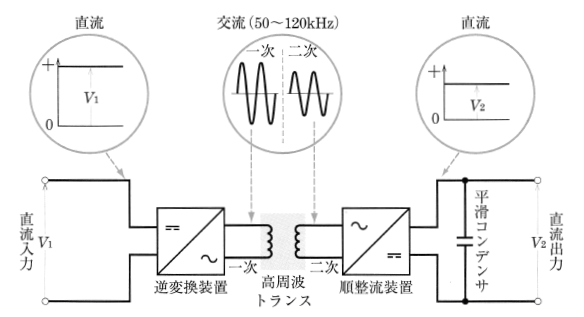
図6はその原理図で、半導体バルブデバイスによって、直流をいったん 50~120[kHz]程度の交流に変換し、これを高周波トランスによって変圧し、整流装置によってふたたび平滑な直流出力をつくり、直流変換を行っています。制御装置によって安定した出力が得られ、数100 mW~ 数10 kWのものが製造されています。
通流率が $d$ のときの直流昇降圧チョッパ回路の平均出力電圧を求める式
$V_d=\displaystyle\frac{d}{1-d}V$
$V_d$[V]:平均出力電圧
$d$:通流率
$V$[V]:電源電圧
電験三種-機械(パワーエレクトロニクス)過去問
2001年(平成13年)問7
直流電源電圧を $V_d$ 、直流チョッパのスイッチング周期を $T$ 、オン期間を $T_{on}$ とした場合、チョッパの平均出力電圧 $V_o$ に関する記述として、誤っているのは次のうちどれか。
- 降圧チョッパの出力電圧 $V_o$ は、理論的には $0~V_d$ の範囲内で連続的に制御できる。
- 降圧チョッパでは、$\displaystyle\frac{T_{on}}{T}$ が $\displaystyle\frac{1}{2}$ のとき、出力電圧 $Vo$ は $\displaystyle\frac{V_d}{4}$ となる。
- 昇圧チョッパの出力電圧 $V_o$ は、直流電源電圧 $V_d$ より低い値には制御できない。
- 昇圧チョッパでは、$\displaystyle\frac{T_{on}}{T}$ が $\displaystyle\frac{1}{2}$ のとき、出力電圧 $V_o$ は $2V_d$ となる。
- 昇降圧チョッパの出力電圧 $V_o$ は、理論的には零から無限大まで連続的に制御できる。
2001年(平成13年)問7 過去問解説
降圧チョッパの出力電圧は、
$\displaystyle\frac{T_{on}}{T_{on}+T_{off}}V_d=\displaystyle\frac{T_{on}}{T}V_d$
降圧チョッパでは、$\displaystyle\frac{T_{on}}{T}$ が $\displaystyle\frac{1}{2}$ のとき、出力電圧 $Vo$ は $\displaystyle\frac{V_d}{2}$ になります。
答え (2)
2005年(平成17年)問8
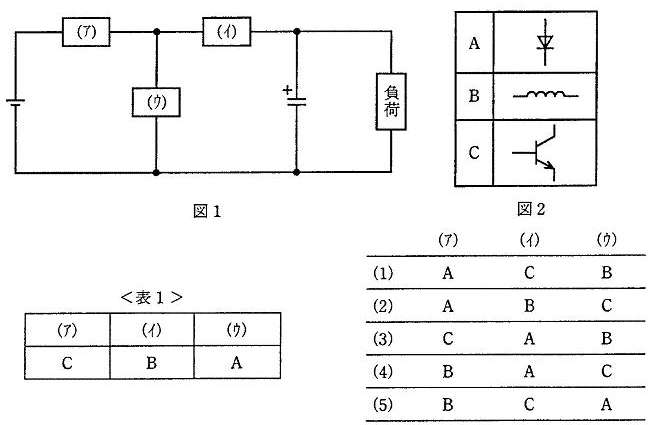
図1は直流チョッパ回路の基本構成図を示している。昇圧チョッパを構成するデバイスを図2より選んで回路を構成したい。表1の降圧チョッパ回路の組合せを参考にして、正しいものを組み合わせたのは次のうちどれか。
ただし、図2に示す図記号の向きは任意に変更できるものとする。
2005年(平成17年)問8 過去問解説
回路のON・OFFの際に発生するコイルの逆起電力をコンデンサに充電して昇圧する回路です。したがって、(ウ)はスイッチの役目をするトランジスタになります。
逆起電力を発生するコイルを(イ)に接続すると平滑回路になって高圧を発生さすことができないので、(ア)がコイルになります。 (イ)は逆流を抑圧するダイオードが適切です。
答え (4)
2010年(平成22年)問10
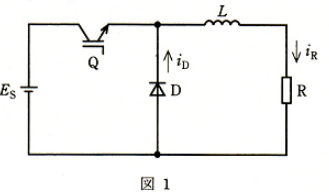
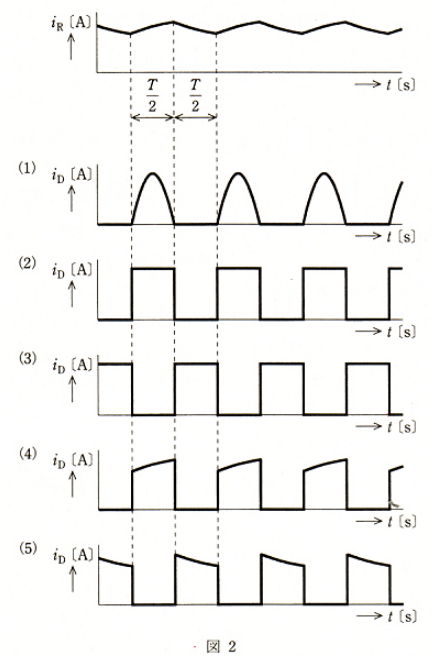
図1は、降圧チョッパの基本回路である。オンオフ制御バルブデバイス $Q_1$ は、IGBTを用いており、$\displaystyle\frac{T}{2}$[s]の期間はオン、残りの$\displaystyle\frac{T}{2}$[s]の期間はオフで、周期 T[s]でスイッチングし、負荷抵抗 $R$ には図2に示す波形の電流 $i_R$[A]が流れているものとする。
このとき、ダイオード D に流れる電流 $i_D$[A]の波形に最も近い波形は、図2の(1)から(5)のうちのどれか。
2010年(平成22年)問10 過去問解説
負荷回路にインダクタンス L が接続されていますので、電流 iR は急激な変化をしないで、流れています。電流の流れ方は、IGBTが ON の時は、電源電圧 ES によってダイオードに逆バイアスがかかっているので、iD=0 となります。
IGBTが OFFの時は、インダクタンス L によって、iR=iD の電流が流れようとします。このときは、電源が OFF なので徐々に電流も減少傾向になります。
この条件を満たす波形は、(5)になります。
答え (5)
2014年(平成26年)問16
図のように他励直流機を直流チョッパで駆動する。電源電圧は $E=200$Vで一定とし、直流機の電機子電圧を $V$ とする。IGBT $Q_1$ 及び $Q_2$ をオンオフ動作させるときのスイッチング周波数は 500Hzであるとする。なお、本問では直流機の定常状態だけを扱うものとする。次の(a)及び(b)の問に答えよ。
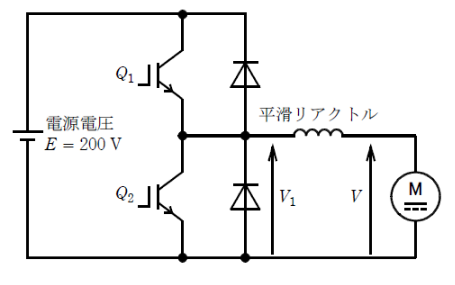
(a) この直流機を電動機として駆動する場合、$Q_2$ をオフとし、$Q_1$ をオンオフ制御することで、$V$ を調整することができる。電圧 $V_1$ の平均値が 150Vのとき、1周期の中で $Q_1$ がオンになっている時間の値[ms]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.75 (2) 1.00 (3) 1.25 (4) 1.50 (5) 1.75
(b) $Q_1$ をオフして $Q_2$ をオンオフ制御することで、電機子電流の向きを(a)の場合と反対にし、直流機に発電動作(回生制動)をさせることができる。この制御において、スイッチングの1周期の間で $Q_2$ がオンになっている時間が 0.4msのとき、この直流機の電機子電圧 $V$[V]として、最も近い $V$ の値を次の(1)~(5)のうちから一つ選べ。
(1) 40 (2) 160 (3) 200 (4) 250 (5) 1000
2014年(平成26年)問16 過去問解説
(1) スイッチングの周波数 $f$ と周期 $T$ の関係は、
$T=\displaystyle\frac{1}{f}=\displaystyle\frac{1}{500}=2$[ms]
$Q_2$ をオフとし、$Q_1$ をオンオフ制御することで、$V$ を調整して、直流電動機の速度制御を行います。この場合は、降圧チョッパ回路になります。$Q_1$ がONのときの時間を TON としたときの出力 $V$ は、
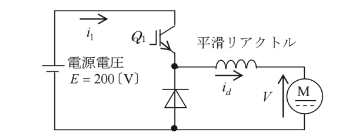
$V=\displaystyle\frac{T_{on}}{T_{on}+T_{off}}E=\displaystyle\frac{T_{on}}{T}E$
$150=\displaystyle\frac{T_{on}}{2}×200$
$T_{on}=1.50$[ms]
答え (4)
(b) $Q_1$ をオフして $Q_2$ をオンオフ制御することで、電機子電流の向きを(a)の場合と反対にし、直流機に発電動作(回生制動)をさせることができます。電機子電流の向きを(a)の場合と反対ですので、昇圧チョッパ回路になります。
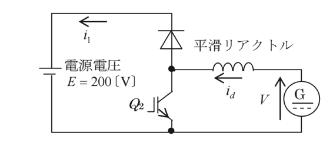
このとき、直流機が起電力 $V$ を発生する発電機となり、電力が電源に回生されて制動力が減速します。回生制動では、V>E となります。
$E=\displaystyle\frac{T_{on}+T_{off}}{T_{off}}V$
$200=\displaystyle\frac{2}{2-0.4}×V$
$V=160$[V]
答え (2)
2015年(平成27年)問10
図のような直流チョッパがある。直流電源電圧 $E=400$V、平滑リアクトル $L=1$mH、負荷抵抗 $R=10$Ω、スイッチSの動作周波数 $f=10$kHz、通流率 $d=0.6$ で回路が定常状態になっている。Dはダイオードである。このとき負荷抵抗に流れる電流の平均値[A]として最も近いものを次の(1)~(5)のうちから一つ選べ。
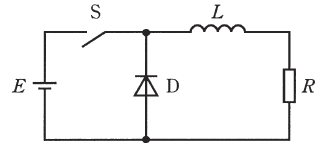
(1) 2.5 (2) 3.8 (3) 16.0 (4) 24.0 (5) 40.0
2015年(平成27年)問10 過去問解説
回路にリアクトルが入っているので、降圧チョッパ回路です。平均出力電圧を $V_D$[V]は、
$V_D=\displaystyle\frac{T_{on}}{T_{on}+T_{off}}E=\displaystyle\frac{T_{on}}{T}E$
$=dE=0.6×400=240$
負荷抵抗に流れる電流の平均値 $I_R$[A]は、
$I_R=\displaystyle\frac{V_D}{R}=\displaystyle\frac{240}{10}=24.0$[A]
答え (4)
通流率 $d$ とは、半導体スイッチング素子がONしている時間の割合のことで、デューティー比ともいいます。
2016年(平成28年)問9
図は、2種類の直流チョッパを示している。いずれの回路もスイッチ S,ダイオード $D$,リアクトル $L$,コンデンサ $C$(図1のみに使用されている。)を用いて、直流電源電圧 $E=200$Vを変換し、負荷抵抗Rの電圧 $v_{d1}$,$v_{d2}$ を制御するためのものである。これらの回路で、直流電源電圧は $E=200$V一定とする。また、負荷抵抗 $R$ の抵抗値とリアクトル $L$ のインダクタンス又はコンデンサ $C$ の静電容量の値とで決まる時定数が、スイッチ S の動作周期に対して十分に大きいものとする。各回路のスイッチSの通流率を 0.7 とした場合、負荷抵抗 $R$ の電圧 $v_{d1}$,$v_{d2}$ の平均値 $V_{d1}$,$V_{d2}$ の値[V]の組合せとして、最も近いものを次の(1)~(5)のうちから一つ選べ。
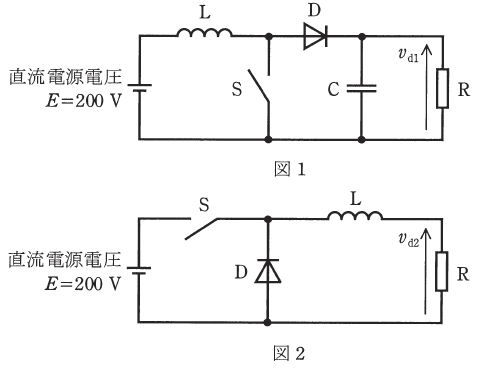
| $V_{d1}$ | $V_{d2}$ | |
| (1) | 667 | 140 |
| (2) | 467 | 60 |
| (3) | 667 | 86 |
| (4) | 467 | 140 |
| (5) | 286 | 60 |
2016年(平成28年)問9 過去問解説
図1は回路に、コンデンサが入っているので昇圧チョッパ回路です。図2は回路にリアクトルが入っているので、降圧チョッパ回路です。通流率を $d$ とすると、
$d=\displaystyle\frac{T_{on}}{T_{on}+T_{off}}=0.7$
割合で考えると、
$T_{on}=0.7$
$T_{on}+T_{off}=1$
ですので、
$T_{off}=1-T_{on}=1-0.7=0.3$
となります。
$V_{d1}=\displaystyle\frac{T_{on}+T_{off}}{T_{off}}E$
$=\displaystyle\frac{1}{0.3}×200≒667$[V]
$V_{d2}=\displaystyle\frac{T_{on}}{T_{on}+T_{off}}E$
$=\displaystyle\frac{0.7}{1}×200=140$[V]
答え (1)





