中学校で習う図形について理解を深めましょう。電験3種の問題は、「図形化」を行うと、理解がしやすくなる問題が多数出題されます。「図形=ひらめき」が必要と思われがちですが、電験3種の電気の問題に必要な数学では、ひらめきよりも知識に基づいた論理的思考が要求されます。ここでは「三平方の定理」を理解し、使いこなせることがキーポイントとなります。
平面図形
平面図形について基本的な用語や公式をまとめています。円周の求め方や扇形の弧の長さの求め方は、必ず覚えておきましょう。
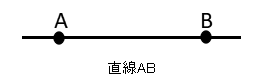 | 点A,Bを通る直線を直線ABといいます。 |
 | 直線のうちAからBまでを線分ABといいます。 |
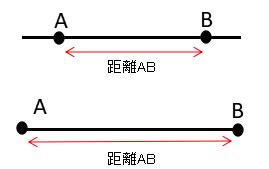 | 直線ABの長さや線分ABの長さを距離といいます。 |
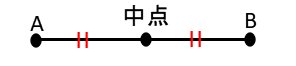 | 線分を2等分する点を、その線分の中点といいます。 |
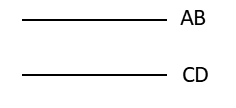 | 2直線ABとCDが平行のとき、AB∥CDとあらわします。 |
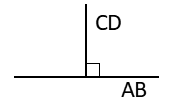 | 2直線ABとCDが垂直のとき、AB⊥CDとあらわします。また2直線が垂直のとき、一方の直線を他方の直線の垂線といいます。 |
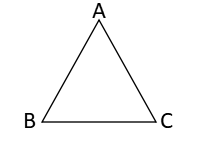 | 三角形ABCを△ABCとあらわします。 |
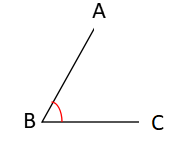 | 角ABCを∠ABCとあらわします。 |
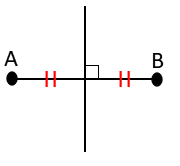 | 線分の中点を通り、その線分に垂直な直線をその線分の垂直二等分線といいます。 |
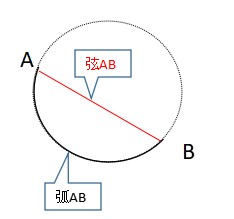 | 円周の一部分を弧といい、$ \stackrel{ \Large \frown }{ AB }$とあらわします。 また、円周上の2点を結ぶ線を弦といいます。 |
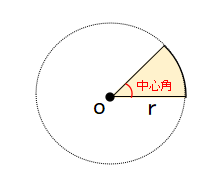 | 2つの半径と弧で囲まれた図形を扇形といいます。また2つの半径で作られた角を中心角といいます。 |
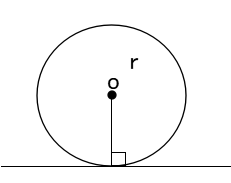 | 円の接線は、接点をとおる半径に垂直になります。 |
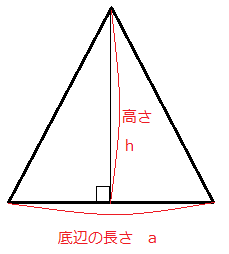 | 三角形の面積の求め方 三角形の底辺をa、高さをhとすると、三角形の面積Sは、 次の公式で求められます。 面積 $ S=\displaystyle \frac{ 1 }{ 2 }ah$ |
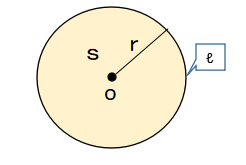 | 円周と円の面積の求め方 円の半径をrとすると、円周ℓと円の面積Sは、次の公式で求められます。 円周 $ ℓ=2πr$ 面積 $ S=πr^2$ |
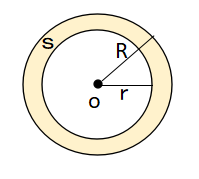 | 円環の面積の求め方 大きな円の半径をR、小さな円の半径をrとすると、円環の面積Sは、次の公式で求められます。 面積 $ S=π(R^2-r^2)$ |
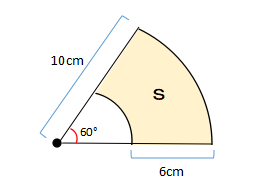
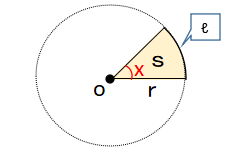 | 扇形の弧の長さと面積の求め方 半径をr、中心角を$ x°$とすると、扇形の弧の長さℓと面積Sは、次の公式で求められます。 弧の長さ $ ℓ=2πr×\displaystyle \frac{ x }{ 360 }$ 面積 $ S=πr^2×\displaystyle \frac{ x }{ 360 }$ |
演習問題1
次の問題が解けますか?
1. 半径が5cmの円周の長さと面積をそれぞれ求めてください。
2. 面積が$ 24πcm^2$の円の直径を求めてください 。
3. 半径10cm,中心角72°のおうぎ形の弧の長さと面積を,それぞれ求めてください 。
4. 半径が6cm,面積が$ 12πcm^2$のおうぎ形があります。
① 中心角の大きさを求めてください。
② おうぎ形の弧の長さを求めてください。
5. 下の図の面積を求めて下さい。
演習問題1の解答
1の解答
円周:$ ℓ=2π×5=10π(cm)$
面積:$ S=π×5^2=25π(cm^2)$
2の解答
$ S=π×r^2$
$ 24π=π×r^2$
$ r=\sqrt{ 24 }=2\sqrt{ 6 }$
直径:$ 4\sqrt{ 6 }(cm)$
3の解答
弧の長さ:$ ℓ=2π×10×\displaystyle \frac{ 72}{ 360 }=4π(cm)$
面積:$ S=π×10^2×\displaystyle \frac{ 72 }{ 360 }=20π(cm^2)$
4の解答
① $ 12π=π×6^2×\displaystyle \frac{x }{ 360 }$
中心角:$ x=120°$
② $ ℓ=2π×6×\displaystyle \frac{ 120 }{ 360 }$
円周:$ ℓ=4π(cm)$
5の解答
面積 $ S=π×10^2×\displaystyle \frac{ 60}{ 360 }-π×4^2×\displaystyle \frac{ 60}{ 360 }=14π(cm^2)$
立体図形
立体図形について覚えて覚えておきたい公式をまとめています。球の表面積の求め方は、必ず覚えておきましょう。
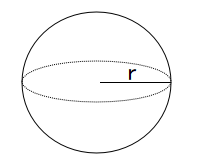
球の表面積と体積の求め方
半径をrの球の表面積Sと体積Vは、次の公式で求められます。
表面積 $ S=4πr^2$
体積 $ V=\displaystyle \frac{ 4 }{ 3 }πr^3$
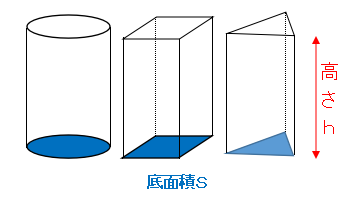
柱の体積の求め方
柱の底面積をS、高さをhとすると柱の体積Vは、次の公式で求められます。
体積 $ V=Sh$
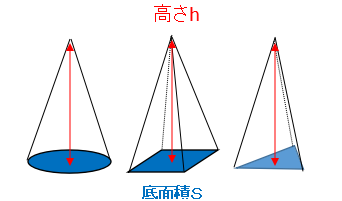
錐の体積の求め方
錐の底面積をS、高さをhとすると柱の体積Vは、次の公式で求められます。
体積 $ V=\displaystyle \frac{ 1 }{ 3 }Sh$
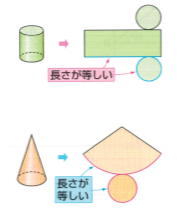
柱・錐の表面積の求め方
柱・錐の表面積は図形を展開しパーツごとの面積を足し合わせます。
図形の角度と三角形の合同と相似
図形の角度や三角形の合同と相似は、電気数学の要となる三角関数やベクトルの基礎となります。また物理現象から電気を考える際にも必要な知識の元となりますので、きっちりと基礎を養っておいてください。
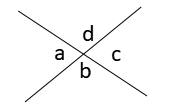
対頂角
二つの直線が交わってできる角のうち、∠aと∠cのように、向かい合った角を対頂角といい∠a=∠cの関係にあります。また、∠bと∠dも対頂角です。∠a=∠c=80°なら、∠b=∠d=180°-80°=100°となります。
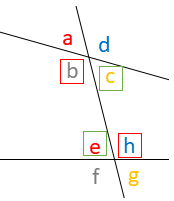
同位角と錯角
2つの直線に1つの直線が交わると8つの角ができます。この8つの角で、∠aと∠eや∠bと∠fのように、同じ位置関係にある角を同位角といいます。
また、∠bと∠hや∠cと∠eのような位置関係にある角を錯角といいます。
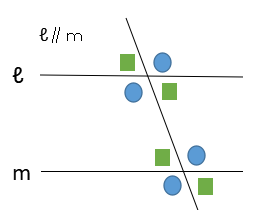
平行線の同位角と錯角
図のように平行線では、同位角と錯角は等しくなります。
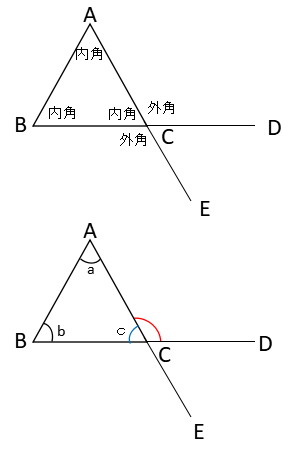
三角形の内角と外角
三角形の内側の角を内角、外側の角を外角といいます。三角形の内角の和は180°です。つまり三角形の3つの角の大きさをすべて足すと180°で、直線になります。
三角形の外角は、これととなりあわない2つの内角の和に等しくなります。下側の図で、
∠a+∠b+∠c=180°(内角の和)
∠ACD+∠c=180°(直線)
この2式から
∠a+∠c=∠ACD
が導きだせます。
三角形の外角は6か所ありますので、どの角度でも対応できるように慣れておいてください。
三角形の合同条件
合同とは、まったく同じ図形同士のことをいいます。三角形の合同条件は、
・3辺がそれぞれ等しいとき
・2辺とその間の角がそれぞれ等しいとき
・1辺とその両端の角がそれぞれ等しいとき
2つの三角形が合同となります。

三角形の相似条件
相似とは、ある図形を拡大または縮小したことをいいます。三角形の相似条件は、
・3組の辺の比がすべて等しいとき
・2組の辺の比が等しく、その間の角が等しいとき
・2組の角がそれぞれ等しいとき
2つの三角形が相似となります。
三平方の定理
平方の定理は、電気計算で重要度大です。必ず使いこなせるようにしておいてください。
三平方の定理(重要)
直角三角形の直角をはさむ2辺の長さをa,b とし,斜辺の長さをc とすると
$ a^2+b^2=c^2$
の関係式が成り立ちます。

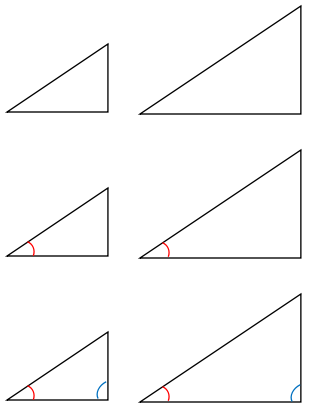
特別な三角比(重要)
直角二等辺三角形と、正三角形を半分にした三角形は角度はそれぞれ 45°, 45°, 90° と 30°, 60°, 90°となります。
この形の三角形は、3辺の長さの比が図のようになります。
30° 斜辺:底辺:高さ=2:$ \sqrt{ 3 }$:1
60° 斜辺:底辺:高さ=2:1:$ \sqrt{ 3 }$
45° 斜辺:底辺:高さ=$ \sqrt{ 2 }$:1:1

演習問題2
次の問題が解けますか?
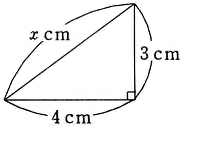
1. 次の図の,x の値を求めてください。
①
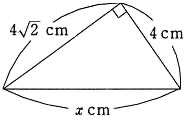
②
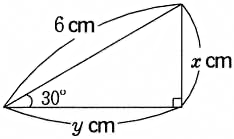
2. 次の図の,x とyの値を求めてください。
①
②
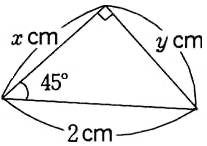
3. 次の図の,x の値を求めてください。
①
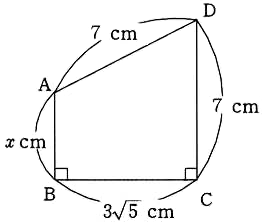
②
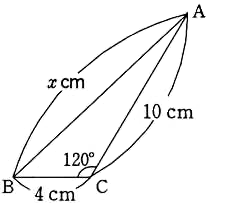
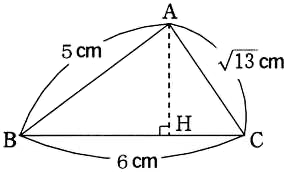
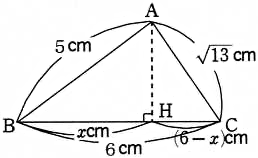
4. 次の図のような△ABCの高さAHを求めてください。
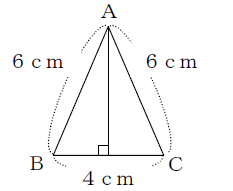
5. 次の図形の面積を求めてください 。
①
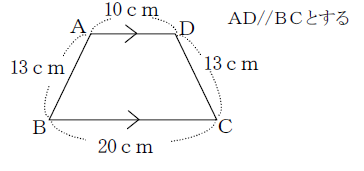
②
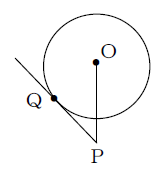
6. 図のPQは半径7㎝の円Oの接線で点Qは接点です。OP=10㎝のときPQの長さを求めてください 。
7. 底辺の半径が6㎝,母線の長さが18㎝の円すいがあります。立体の体積を求めてください。

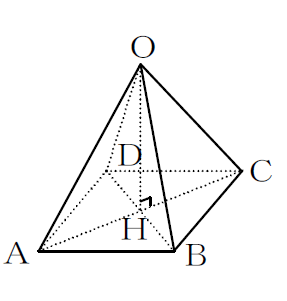
8. 底面の一辺の長さが6㎝,他の辺の長さがすべて9㎝の正四角錐があります。次の問いに答えてください。
① 高さOHを求めてください。
② 立体の体積を求めてください。
③ 立体の表面積を求めてください。
演習問題2の解答
1の解答
①
$ x^2=4^2+3^2$
$ x^2=16+9=25$
$ x=5$ (答え)
②
$ x^2=4^2+(4\sqrt{ 2 })^2$
$ x^2=4^2+(4\sqrt{ 2 })^2$
$ x^2=16+32=48$
$ x=4\sqrt{ 3 }$ (答え)
2の解答
①
$ x:6=1:2$
$ x=3$ (答え)
$ 3:y=1:\sqrt{ 3 }$
$ y=3\sqrt{ 3 }$ (答え)
②
$ x:2=1:\sqrt{ 2 }$
$ \sqrt{ 2 }x=2$
$ x=\displaystyle \frac{ 2 }{ \sqrt{ 2 } }$
$ x=\sqrt{ 2 }$ (答え)
$ y=\sqrt{ 2 }$ (答え)
3の解答
①
△DAEで三平方の定理を使います。
$ 7^2=3\sqrt{ 5 }^2+a^2$
$ a^2=49-45=4$
$ a=2$
$ x=7-a=7-2=5$ (答え)
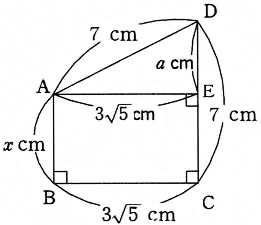
②
△ACDは∠60°の三角形なので
$ 10:a=2:1$
$ a=5$
$ 10:b=2:\sqrt{ 3 }$
$ b=5\sqrt{ 3 }$
△ABDで三平方の定理を使います。
$ x^2=(4+5)^2+(5\sqrt{ 3 })^2$
$ x^2=81+75=156$
$ x=2\sqrt{ 39 }$ (答え)
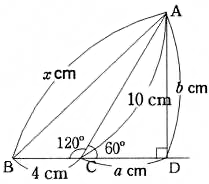
4の解答
△ABHで三平方の定理を使います。
$ 5^2=x^2+AH^2$$ AH^2=25-x^2$ ・・・ ①
△ACHで三平方の定理を使います。
$ (\sqrt{ 13 })^2=(6-x)^2+AH^2$
$ AH^2=13-(6-x)^2$ ・・・ ②
①、②より
$ 25-x^2=13-(6-x)^2$
$ 12x=48$
$ x=4$ ・・・ ③
③を①に代入します。
$ AH^2=25-4^2$
$ AH^2=25-16=9$
$ AH=4$ (答え)
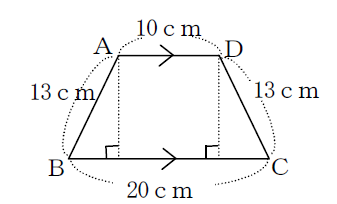
5の解答
① △ABCの高さをh とすると三平方の定理より
$ 6^2=2^2+h^2=\sqrt{ 36-4 }=\sqrt{ 32 }=4\sqrt{ 2 }$
面積は $ 4×4\sqrt{ 2 }×\displaystyle \frac{ 1 }{ 2 }=8\sqrt{ 2 }(cm^2)$ (答え)
② 図のように垂線を書きます。台形の高さをhとすると、三平方の定理より
$ 13^2=5^2+h^2$
$ h=\sqrt{ 169-25 }=\sqrt{ 144 }=12$
台形の面積 $ (10+20)×12×\displaystyle \frac{ 1 }{ 2 }=180 (cm^2)$ (答え)
6の解答
円の接線は、接点をとおる半径に垂直になります。△OPQは直角三角形です。三平方の定理より
$ PQ=\sqrt{ 10^2-7^2 }=\sqrt{ 100-49 }=\sqrt{ 51 }(cm)$ (答え)
7の解答
円錐の高さをhとすると
$ h=\sqrt{ 18^2-6^2 }=\sqrt{ 324-36 }=12\sqrt{ 2 }$
錐の体積 $ V=\displaystyle \frac{ 1 }{ 3 }×底面積S×高さh$
$ V=\displaystyle \frac{ 1 }{ 3 }×6×6×π×12\sqrt{ 2 }=144\sqrt{ 2 }π(cm^3)$ (答え)
8の解答
① △HABは直角二等辺三角形ですので、$ AH:AB=1:\sqrt{ 2 }$となります。よって、
$ AH:6=1:\sqrt{ 2 }$
$ 6=\sqrt{ 2 }AH$
$ AH=3\sqrt{ 2 }$
△OAHは直角三角形ですので、
$ OH=\sqrt{ OA^2-AH^2 }$
$ OH=\sqrt{ 9^2-(3\sqrt{ 2 })^2 }=\sqrt{ 81-18 }=3\sqrt{ 7 }(cm)$ (答え)
② 錐の体積 $ V=\displaystyle \frac{ 1 }{ 3 }×底面積S×高さh$
$ V=\displaystyle \frac{ 1 }{ 3 }×6×6×3\sqrt{ 7 }=36\sqrt{ 7 }(cm^3)$ (答え)
③ △OABは二等辺三角形ですので、高さをhとすると
$ h=\sqrt{ 9^2-3^2 }=\sqrt{ 81-9 }=\sqrt{ 72 }=6\sqrt{ 2 }$
△OABの面積$ =6×6\sqrt{ 2 }÷2=18\sqrt{ 2 }$
4つの側面は合同なので、
側面の面積$ =4×18\sqrt{ 2 }=72\sqrt{ 2 }$
側面の面積に底面積を足すと表面積になります。
$ 36+72\sqrt{ 2 }(cm^2)$ (答え)