ベクトルと複素数は、高校2年生までの数学で習う範囲です。電験3種の交流回路はベクトル図を使って考えることがポイントになります。また、交流回路の計算をするのに複素数の知識が必須となります。必ずマスターしてください。
絶対値とベクトル
絶対値について
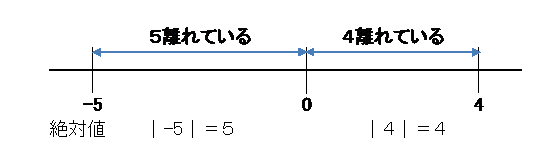
絶対値とは、数直線上で「原点からある数までの距離(大きさ)」のことをいいます。絶対値は、$ | x |$というふうに表します。絶対値は距離を表していますので,必ず0以上の実数になります。
絶対値(例題)
$ |-2|+|5|=7$
$ |\sqrt{ 2 }- 2|=-(\sqrt{ 2 }-2)=2-\sqrt{ 2 }$
$ |x+3|=5$ を満たすxの値は? 答え x=2 または -8
ベクトル
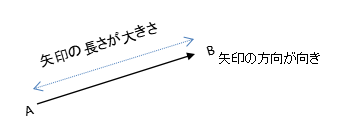
ベクトルとは、向きと大きさを持つ量のことです。有向線分で表され、その矢印がベクトルの向きを意味し、長さがベクトルの大きさを意味します。点Aから点Bの直線をベクトルで表すと、$ \vec{ AB }$ や $ \dot{ AB }$ と書きます。
ベクトルの相等(等しいこと)
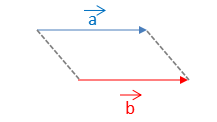
ベクトルの大きさと向きが等しいとき、ベクトルは相等するといいます。相等していると,一方のベクトルを平行移動して他方のベクトルに重ね合わせることができます。
$ \vec{ a }= \vec{ b }$
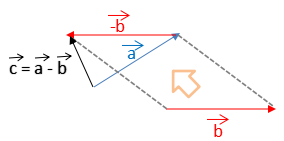
ベクトルの和
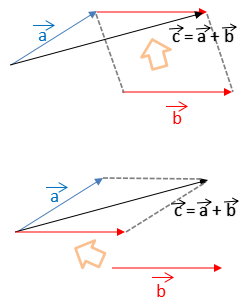
$ \vec{ a }$と$ \vec{ b }$の和を$ \vec{ c }$とすれば、右図のように移動させます。平行四辺形を描き、その対角線を引いて作図してもできます。
$ \vec{ c }= \vec{ a }+\vec{ b }$
ベクトルの差
$ \vec{ a }$と$ \vec{ b }$の差を$ \vec{ c }$とすれば、$ -\vec{ b }$は$ \vec{ b }$の逆ベクトルと考え移動させます。
$ \vec{ c }= \vec{ a }-\vec{ b }$
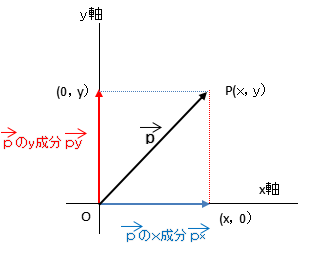
ベクトルの大きさ
ベクトルの和や差の逆として、ベクトルは分解して考えることができます。わかりやすいように直交座標上で説明します。
x-y平面座標上の点Oから点P(x,y)に向かうベクトル $ \vec{ p }$ が与えられたとき、
$ \vec{ p }$ のxとyの成分
$ \vec{ px }$ と $ \vec{ py }$
のように分解することができます。
ここで、注目してほしいのが「ベクトルは向きと大きさ(長さ)を表している」ということです。これに対してベクトルの大きさ(長さ)は単なる1つの数でスカラーといいます。ベクトルの大きさ(長さ)は,絶対値記号を用いて表します。 $ \vec{ p }$ の大きさ(スカラー量)は、 $ |\vec{ p }|$ と書きます。
また、図に注目してみると、直角三角形ということに気づくと思います。つまり、$ \vec{ p }$ の大きさ $ |\vec{ p }|$ を三平方の定理を用いて表現すると,
$ \vec{ p }=\sqrt{ x^2+y^2 }$
虚数と複素数
実数と虚数
実数とは2乗すれば正となる数のことで、虚数とは2乗すれば-1となる数のことです。尚、虚数は実在しない数で、計算上でのみ使用します。
定義では非常に分かりにくいと思いますので、以下を参考に理解してください。
平方根は2乗すればその数になります。
方程式 $ x^2=4$ の答えは $ x=±2$ です。では方程式、$ x^2=-4$ の答えは?この答えは、実数の範囲には存在しません。そこで、虚数という考え方が必要になります。「想像上の数」 であるのですが、電気計算の世界では理解が不可欠なのです。電気分野では虚数は $j$ として表します(数学的には $i$ )。虚数の定義として$ x^2=-1$ の1つの解、$\sqrt{-1 }$ を虚数単位といい、 $j$ で表します。
$j=\sqrt{-1 }$
$j^2=-1$
電気計算では、虚数や複素数は非常に便利なツールとなります。電験3種の勉強を進めて行けば、その有難さに気づくと思います。
複素数
複素数とは、実数と虚数を組み合わせたものです。任意の実数 a,b に対して a+jb で表される数を複素数といいます。このとき「aを実部」、「bを虚部」といいます。
複素数の計算は文字式含む式の計算規則と同じように計算します。ただし、「$j^2$」が登場すれば、「$j^2=-1$」と、置き換えます。
<例>
$ (2+j3)+(4-j)=(2+4)+j(3-1)=6+j2$
$ (2+j3)(1-j4)=2-j8+j3-j^212=2-j5-(-1)×12=14-j5$
複素数の有利化 複素数の分数型は、分母に「$j$」が残らないように計算します。ルートが分母に入った式の有理化と同じ考え方です。
<例>
$ \displaystyle \frac{ 2 }{ j }=\displaystyle \frac{ 2×j }{ j×j }=\displaystyle \frac{ j2 }{ j^2 }=\displaystyle \frac{ j2 }{ -1 }=-j2$
$ \displaystyle \frac{ 1-j }{ 1+j }=\displaystyle \frac{ (1-j)^2 }{ (1+j)(1-j) }=\displaystyle \frac{ 1-j2-1 }{ 1-j^2 }=\displaystyle \frac{ -j2 }{ 1-(-1) }=\displaystyle \frac{ -j2 }{ 2 }=-j$
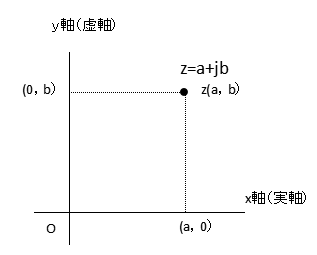
複素平面
複素数「 $ z=a+jb $ 」は、複数の成分を持つ数ですので、一本の数直線の上に並べて大小の比較などをすることができません。そこで、軸を増やし、平面上に表わす方法が考えられました。
x-y平面座標上において, x軸を実部, y軸に虚部を対応させて,複素数を表したものを複素平面といいます。またガウス平面ともいいます。
このように表すことで複素数が非常に分かり易くなります。複素数値を平面上に表わす方法で、点の位置を指定するために、複素平面の原点から複素数zの点まで矢印を引きます。すると、ベクトルのように考えることができるようになります。
複素数の極形式
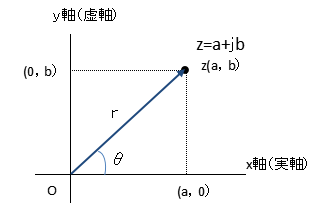
複素数「 z」の矢印の長さを「 r 」とし、この矢印の実軸からの角度をθで表します。反時計回りの角度がプラスと考え、時計回りをマイナスと考えます。この実軸とのなす角を偏角(argument)といい、「 arg z 」と表わします。尚、電気の世界では、偏角のことを位相角といいます。
「 r 」は複素数zの原点からの距離を表しています。原点からの距離はベクトルと同じように考えることができ、「絶対値」で表します。
また、三角関数を思い出してください。複素数「 $ z=a+jb $ 」を「 r 」を斜辺とする直角三角形と考えてみます。なす角がθなので、直角三角形の底辺は「 rcosθ 」、高さは「 rsinθ 」となります。この底辺と高さを複素数「 $ z=a+jb $ 」に対応させてみますと、
$ z=a+jb=rcosθ+jrsinθ=r(cosθ+jsinθ)$
$ θ=tan^{ -1 }\displaystyle \frac{ b }{ a }$
複素数zを絶対値と位相角だけで表す方法もあります。
$ z=|z|∠θ$
このような表し方を、複素数の極形式といいます。
複素数の指数形式
電験3種で出題される数学の範囲は超えていますが、複素数の指数形式というものがあります。なれると大変便利なので、概念だけでも掴んでおいてください。
下記の式で定義される数eを自然対数の底またはネイピア数といいます。
$ e=\displaystyle \lim_{ h \to \infty } (1+\displaystyle \frac{ 1 }{ h })^h =2.71828….$
自然対数の底「 $ e$ 」とは「 $ π$ 」のようなもので、数学の定数の一つです。この自然対数の底「 $ e$ 」に関してオイラーの公式というものが成立します。
オイラーの公式
$ e^{ jθ }=cosθ+jsinθ$
オイラーの公式を複素数「 $ z=a+jb=r(cosθ+jsinθ)$ 」にあてはめると、
$ z=a+jb=r(cosθ+jsinθ)=re^{ jθ }=|z|e^{ jθ }$
$ |z|e^{ jθ }$ のような表し方を、複素数の指数形式といいます。この指数形式は、加法定理や微分積分などで使うと、難しい三角関数を使わずに簡単な指数法則で計算できるようになります。