第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「直流回路の基本問題」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「直流回路の基本問題」の過去問題も解説しています。
- 電流と電圧
- オームの法則
- 短絡と開放
- 直列回路
- 並列回路
- 抵抗の直並列接続
- 電圧降下
- 電験三種-理論の過去問解説:直流回路の基本問題
- 1997年(平成9年)問4【電験理論の過去問題】
- 1998年(平成10年)問5【電験理論の過去問題】
- 2001年(平成13年)問3【電験理論の過去問題】
- 2003年(平成15年)問6【電験理論の過去問題】
- 2004年(平成16年)問4【電験理論の過去問題】
- 2006年(平成18年)問6【電験理論の過去問題】
- 2008年(平成20年)問6【電験理論の過去問題】
- 2009年(平成21年)問6【電験理論の過去問題】
- 2012年(平成24年)問6【電験理論の過去問題】
- 2013年(平成25年)問5【電験理論の過去問題】
- 2013年(平成25年)問8【電験理論の過去問題】
- 2014年(平成26年)問6【電験理論の過去問題】
- 2015年(平成27年)問4【電験理論の過去問題】
- 2017年(平成29年)問5【電験理論の過去問題】
- 2017年(平成29年)問7【電験理論の過去問題】
- 2018年(平成30年)問6【電験理論の過去問題】
電流と電圧
電流の大きさ
導体に流れる電流は、電荷を持つ自由電子の移動によるものです。導体の原子から飛び出した自由電子が静電気力を受けて一斉に同じ方向に動き出すと電流になります。
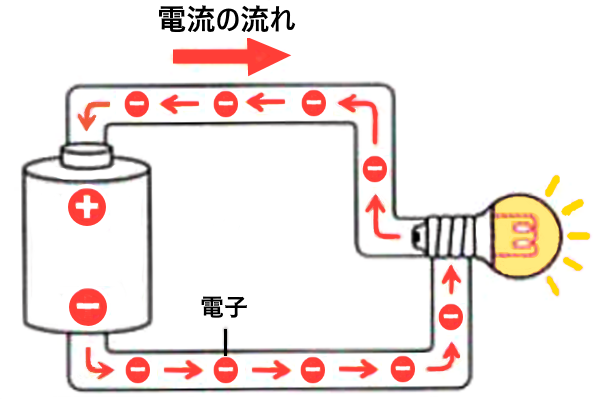
電流の向きは自由電子の移動方向と逆方向と定義されています。自由電子は負電荷です。自由電子が動くときは、正電荷が逆方向に動きます。つまり、電流の向きは正電荷が動く方向です。
電流の大きさは、単位時間に通過する電荷の流量です。「1秒間に 1[C]の電荷が流れるときの電流の大きさを 1(単位:アンペア[A])」と決められています。
$t$[s]の間に $q$[C]の電荷が流れるときの電流の大きさ $I$[A]は、次の式で表されます。
$I=\displaystyle \frac{ q }{ t }$[A]
電圧の大きさ
電気には位置に関係する電位(単位:ボルト[V])という考え方があります。電位は 1[C]の正電荷が持つ電気的な位置エネルギーです。
2点間の電位の差を電位差 $V$(単位:ボルト[V])といいます。電位差のことを「電圧」ともいいます。ある点の電圧の大きさを表すときは、基準点 0[V]からの大きさとして表します。実用上、電位の基準点は大地としています。
電気は水によく例えられます。水と同じように、電流は位置(電位)の高い方から低い方へと流れます。また、同じ位置(同電位)の場合は電流は流れないと考えておいてください(特殊な条件下では例外もあります)。
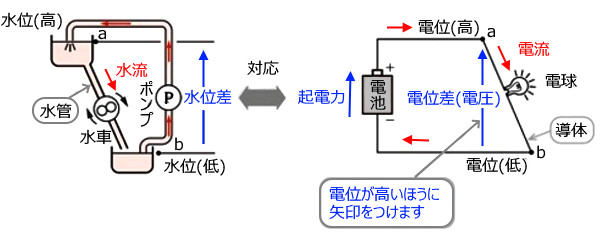
オームの法則
電圧と電流の向きと大きさが時間によって変化しない電気の流れ方を直流といいます。直流電圧と直流電流を表すときは、大文字を使って $V$ 及び $I$ と表わします。素子間の電圧と素子を流れる電流が比例するとき、この素子を抵抗 $R$(単位:オーム[Ω])といいます。
電圧、電流、抵抗の間には「オームの法則」が成り立ち、その内容は次のようになります。
電流は電圧に比例し、抵抗に反比例する
「オームの法則」を式で表すと次のようになり、これは電気回路において電圧、電流、抵抗の関係を表す基本となる公式です。
オームの法則
$V=IR$
$V$[V]:電圧 単位はボルト
$I$[A]:電流 単位はアンペア
$R$[Ω]:抵抗 単位はオーム
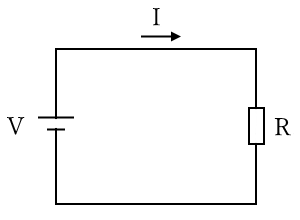
電圧を求める場合:$V=IR$
電流を求める場合:$I=\displaystyle \frac{V}{R}$
抵抗を求める場合:$R=\displaystyle \frac{V}{I}$
公式をそれぞれ変形させて使います。
短絡と開放
オームの法則、$\boxed{ I=\displaystyle \frac{V}{R} }$ の式から次のことがわかります。
抵抗 $R$ が大きいと流れる電流の値は小さくなる
抵抗 $R$ が小さいと流れる電流の値は大きくなる
つまり、抵抗がゼロの回路に電源だけを接続すると、回路にはとても大きな電流が流れます。この状態を「短絡状態」といいます。また、抵抗が無限大の回路には、電流は流れません。このときは、回路が接続されていないとも考えることができます。この状態を「開放状態」といいます。
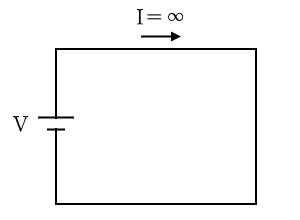
抵抗がないときは、無限大の電流が流れる
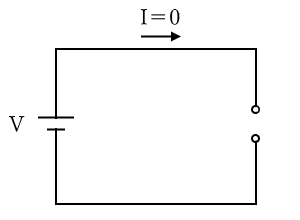
抵抗の大きさが無限大のときは、電流は流れない
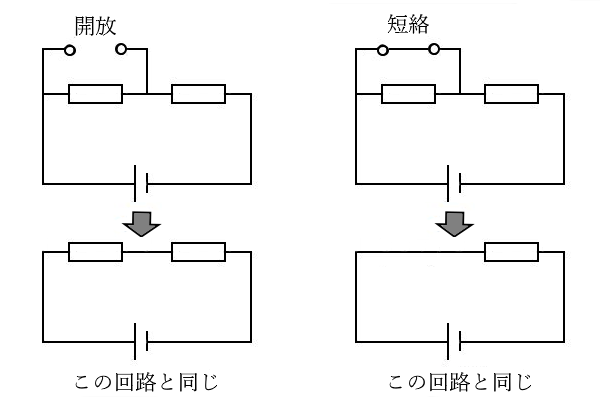
電気回路における短絡とは、「電気回路の2点以上を導線で接続すること」または、「導線に置き換えること」を意味します。短絡すると抵抗 0Ω の経路が作られます。
電気回路における開放とは、「電気回路の導線を切り取ること」を意味します。開放すると電流の通り道がなくなるので、無限大の抵抗が接続されたことと同じになります。
ここで注意が必要なのが、短絡した2点間の電流は 0[A]になるとは限りません。また開放した2点間の電圧は 0[V]になるとは限りません。
直列回路
直列回路の合成抵抗
複数の抵抗を直列に接続した回路のことを直列回路といいます。これらの抵抗を一つの抵抗にまとめたものを合成抵抗といいます。直列回路の合成抵抗は各抵抗値を足して求めることができます。
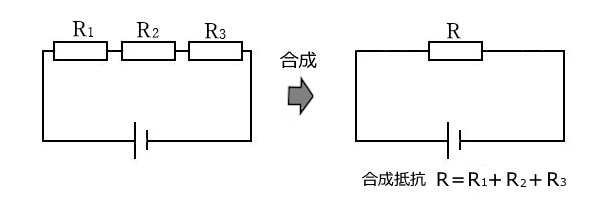
図の合成抵抗 $R$ を求める式は、 $\boxed{ R=R_1+R_2+R_3 }$ になります。
直列回路の電圧
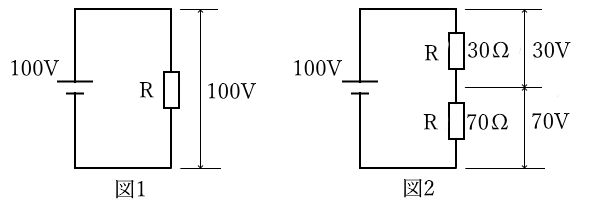
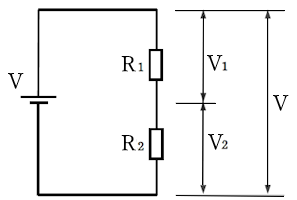
図1のように、抵抗一つの回路に電源を接続して電圧をかけると、その抵抗には電源電圧と同じ電圧がかかります。図2のように複数の抵抗を接続した場合、各抵抗にかかる電圧は、その抵抗値に応じて比例配分されます。
図2の直列回路の抵抗値は、$R_1$=30[Ω]、$R_2$=70[Ω]となっています。各抵抗にかかる電圧は、その抵抗値に応じて比例配分されるため、電源電圧の 100[V]を $R_1$ の 30[Ω]と $R_2$ の 70[Ω]で比例配分すると、30[Ω]にかかる電圧は 30[V]、70[Ω]にかかる電圧は 70[V]になります。
直列回路の各抵抗にかかる電圧は その抵抗値に応じて比例配分されますが、そのことを表す公式は次のようになります。
分担電圧を求める公式
$V_1=\displaystyle \frac{R_1}{R_1+R_2}×V$
$V_2=\displaystyle \frac{R_2}{R_1+R_2}×V$
$V$:全電圧(電源電圧)
$V_1$:抵抗 $R_1$ にかかる電圧
$V_2$:抵抗 $R_2$ にかかる電圧
抵抗が3 つ接続されている場合の式は、$V_1=\displaystyle \frac{R_1}{R_1+R_2+R_3}×V$,$V_2=\displaystyle \frac{R_2}{R_1+R_2+R_3}×V$,$V_3=\displaystyle \frac{R_3}{R_1+R_2+R_3}×V$ になります。
電源の直列接続
直流電源には (+) (-) の極性があるため、電源を同じ向きに接続した場合と逆向きに接続した場合では、全電圧(合成電圧)は異なる値になります。
電源を同じ向きで直列に接続した場合
複数の電源を同じ向きで直列に接続した場合の全電圧(合成電圧)の求め方は、それぞれの電圧の和で求めます。

上図の全電圧は、24 + 12 = 36 で、36 [V] になります。このとき、抵抗 $R$ にかかる電圧も 36 [V] になります。
電源を逆向きで、直列に接続した場合
複数の電源を逆向きで直列に接続した場合の全電圧(合成電圧)の求め方は、それぞれの電圧の差で求められます。

上図の全電圧は、24 - 12 = 12 で、12 [V] になります。このとき、抵抗 $R$ にかかる電圧も 12 [V] になります。
直列回路の電流
直流の電流は電源の (+) 側から (-) 側に向かって流れます。また、直列回路に流れる電流は「どの地点も同じ値になる」といった決まりがあります。
電源が逆向きにつながっている場合は、電圧が高いほうの電源の(+) 側から (-) 側に向かって、電流は流れます。

図1 の回路では、抵抗 $R_1$ に流れる電流 $I_1$ と、 抵抗 $R_2$ に流れる電流 $I_2$ は、同じ値になります。$I_1=I_2$
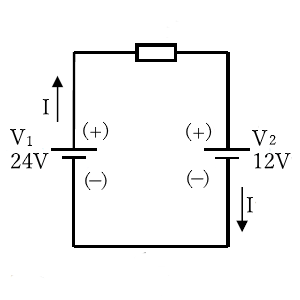
図2 の回路図の電源は、$V_2$ よりも $V_1$ のほうが電圧は高いので、電源 $V_1$ の (+) から (-) に向かって電流は流れます。
並列回路
並列回路の合成抵抗
抵抗が複数ある場合は、次の公式で合成抵抗 $R$ を求めることができます。
並列回路の合成抵抗を求める公式①
$R=\displaystyle \frac{1}{\displaystyle \frac{1}{R_1}+\displaystyle \frac{1}{R_2}+\displaystyle \frac{1}{R_3}}$
この公式は、抵抗が2つの場合や、さらに抵抗の数が増えた場合でも使うことができます。

抵抗が2つの場合は、次の公式で合成抵抗 $R$ を求めることができます。
並列回路の合成抵抗を求める公式②
$R=\displaystyle \frac{R_1R_2}{R_1+R_2}$
この公式は、抵抗が2つの場合のみ使うことができます。
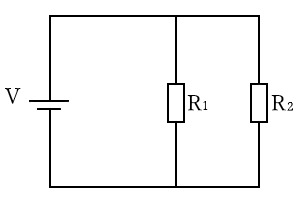
並列回路の電圧
複数の抵抗を並列に接続した場合、各抵抗にかかる電圧は全て等しくなります。
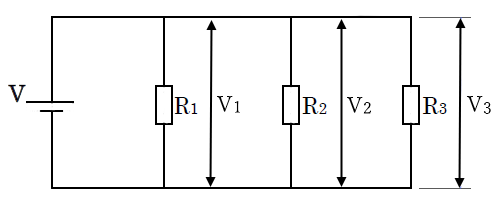
並列回路の各電圧の関係式は、 $V=V_1=V_2=V_3$ となります。
並列回路の電流
並列回路を流れる電流は、流れる地点によって違う値になります。並列回路を流れる電流は、次の公式で求めることができます。
並列回路を流れる電流を求める公式
$I=\displaystyle \frac{V}{R}$ または、$I=I_1+I_2$
$I_1=\displaystyle \frac{V}{R_1} 、I_2=\displaystyle \frac{V}{R_2}$
$I$:回路全体に流れる全電流
$I_1$:$R_1$ を流れる電流
$I_2$:$R_2$ を流れる電流
$R$:$R_1$、$R_2$ の合成抵抗
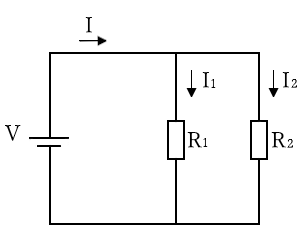
並列回路の電流の求め方には、電流の分流(分担電流)を求める方法があります。
「抵抗 $R_1、R_2$ を流れる電流 $I_1、I_2$ は、全電流 $I$ を各抵抗値に応じて逆比例配分した値になる」
といった法則で、そのことを表す公式は次のようになります。
電流の分流 (分担電流) を求める公式
$I_1=\displaystyle \frac{R_2}{R_1+R_2}×I$
$I_2=\displaystyle \frac{R_1}{R_1+R_2}×I$
$I$:全電流
$I_1$:$R_1$ を流れる電流
$I_2$:$R_2$ を流れる電流

抵抗の直並列接続
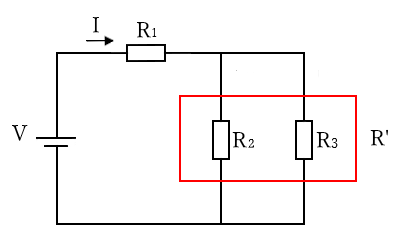
直列接続と並列接続が組み合わされた回路の合成抵抗の求め方を考えます。$R_2$ と $R_3$ の並列部分の合成抵抗 $R’$ を求めます。
$R’=\displaystyle \frac{ R_2R_3}{ R_2+R_3 }$
$R_1$ と $R’$ が直列に接続されていると考え合成抵抗 $R$ を求めます
$R=R_1+\displaystyle \frac{ R_2R_3}{ R_2+R_3 }$
電圧降下
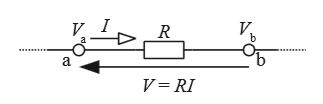
オームの法則は「点aの電圧 $V_a$ が点bの電圧 $V_b$ よりも $V$ だけ高いと電流 $I$ が抵抗 $R$ を点aから点bに向かって流れる」ということです。
これは、「電流 $I$ が抵抗 $R$ を点aから点bに向かって流れると、点bの電圧 $V_b$ が点aの電圧 $V_a$ よりも $V$ だけ低くなる」とも考えることができます。
言い換えれば、「抵抗 $R$ の電圧降下は $V$ 」と言えます。電圧降下の考え方は非常に重要ですので覚えておいてください。
電験三種-理論の過去問解説:直流回路の基本問題
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1997年(平成9年)問4【電験理論の過去問題】
図のような直流回路において、抵抗 $R$[Ω]の値として、正しいのは次のうちどれか。
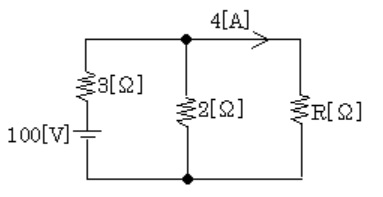
(1) 2.2 (2) 4.0 (3) 8.8 (4) 10.3 (5) 15.5
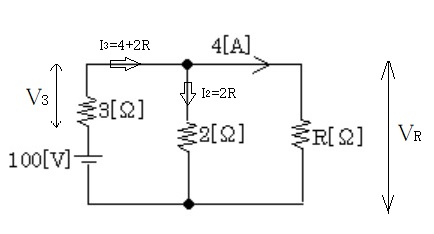
抵抗 $R$[Ω]と 2[Ω]の並列回路の電圧を $V_R$[V]とすると $V_R=4R$[Ω]となります。2Ωの抵抗に流れる電流を $I_2$[A]、3Ωの抵抗に流れる電流を $I_3$[A] 及び電圧降下を $V_3$[V]とし、解いていきます。
2Ωの抵抗に流れる電流を $I_2$[A]は、
$I_2=\displaystyle \frac{ V_R}{ 2 }=2R$[A]
3Ωの抵抗に流れる電流を $I_3$[A]と電圧降下を $V_3$[V]は、
$I_3=4+I_2=4+2R$[A]
$V_3=3I_3=3(4+2R)=12+6R$[V]
$V_3+V_R=100$[V]ですので、
$12+6R+4R=100$
$10R=88$
$R=8.8$[Ω]
答え (3)
1998年(平成10年)問5【電験理論の過去問題】
図のような直流回路において、$R=10$[Ω]のときは $I=5$[A]であり、$R=8$[Ω]にしたときは $I=6$[A]であった。この場合、電源電圧 $V$[V]の値として、正しいのは次のうちどれか。
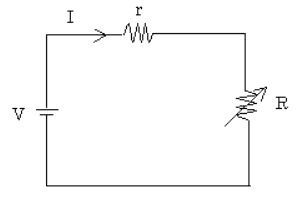
(1) 35 (2) 40 (3) 48 (4) 50 (5) 60
$V=I(r+R)$の関係式が成り立つので、題意より
$V=5(r+10)$ … (1)
$V=6(r+8)$ … (2)
(1),(2)式を解くと、
$5(r+10)=6(r+8)$
$5r+50=6r+48$
$r=2$
(1)式より
$V=5(2+10)=60$[V]
答え (5)
2001年(平成13年)問3【電験理論の過去問題】
図のような直流回路において、電源を流れる電流は、100[A]であった。このとき、80[Ω]の抵抗に流れる電流 $I$[A]の値として、正しいのは次のうちどれか。
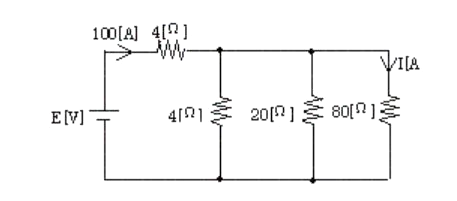
(1) 3 (2) 4 (3) 5 (4) 6 (5) 7
4Ωの抵抗に流れる電流を $I_1$[A]、20Ωの抵抗に流れる電流を $I_2$[A]とすると、
$I_1+I_2+I=100$ … (1)
4Ωの抵抗の電圧、20Ωの抵抗の電圧、80Ωの抵抗の電圧は $E$[V]に等しいので、
$E=4I_1=20I_2=80I$ … (2)
(2)式より
$I_1=20I$ … (3)
$I_2=4I$ … (4)
(3)、(4)式を(1)式に代入する
$20I+4I+I=100$
$25I=100$
$I=4$[A]
答え (2)
2003年(平成15年)問6【電験理論の過去問題】
図のような直流回路において、電源電圧が $E$[V]であったとき、末端の抵抗の端子間電圧の大きさが 1[V]であった。このときの電源電圧 $E$[V]の値として、正しいのは次のうちどれか。
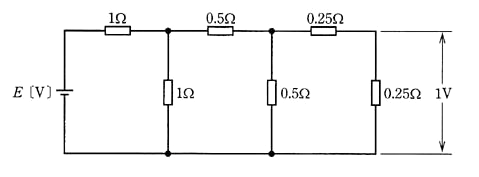
(1) 34 (2) 20 (3) 14 (4) 6 (5) 4
わかるところから順次、電圧と電流を計算していきます。
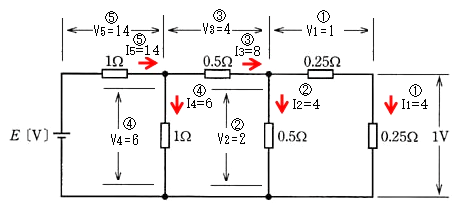
- $0.25×I_1=1$ $I_1=4$
$0.25×4=V_1$ $V_1=1$
- $V_2=1+V_1=2$
$0.5×I_2=2$ $I_2=4$
- $I_3=I_1+I_2=8$
$V_3=0.5×8=4$
- $V_4=V_2+V_3=6$
$1×I_4=6$ $I_4=6$
- $I_5=I_3+I_4=14$
$V_5=1×14=14$
$E=V_4+V_5=20$[V]
答え (2)
2004年(平成16年)問4【電験理論の過去問題】
図の抵抗回路において、端子 a,b間の合成抵抗 $R_{ab}$ [Ω]の値は $1.8R$ [Ω]であった。このとき、抵抗 $R_x$ [Ω]の値として、正しいのは次のうちどれか。
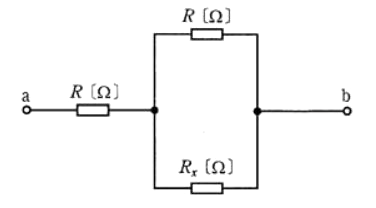
(1) R (2) 2R (3) 3R (4) 4R (5) 5R
合成抵抗 $R_{ab}$ は
$R_{ab}=R+\displaystyle \frac{ RR_x}{ R+R_x }=1.8R$
$R(R+R_x)+RR_x=1.8R(R+R_x)$
$R^2+RR_x+RR_x=1.8R^2+1.8RR_x$
$0.2RR_x=0.8R^2$
$R_x=4R$
答え (4)
2006年(平成18年)問6【電験理論の過去問題】
図のように、即知の直流電源 $E$[V]、未知の抵抗 $R_1$[Ω]、即知の抵抗 $R_2$[Ω]及び $R_3$[Ω]からなる直流回路がある。抵抗 $R_3$[Ω]に流れる電流 $I_3$[A]であるとき、抵抗 $R_1$[Ω]を求める式として、正しいのは次のうちどれか。
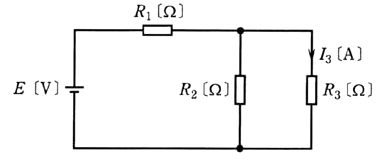
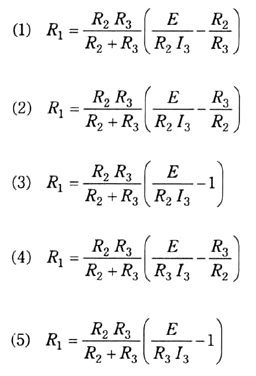
抵抗 $R_1$,$R_2$に流れる電流をそれぞれ $I_1$,$I_2$、電圧をそれぞれ $V_1$,$V_2$とします。
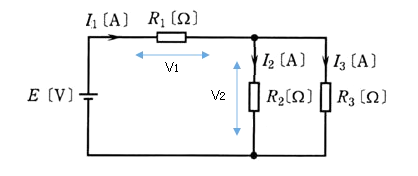
$V_2=R_2I_2=R_3I_3$
$I_2=\displaystyle \frac{ R_3I_3}{ R_2 }$ … (1)
$I_1=I_2+I_3$ … (2)
$E=V_1+V_2=I_1R_1+I_3R_3$
$R_1=\displaystyle \frac{ E-I_3R_3}{ I_1 }$ … (3)
(1)式を(2)式に代入する
$\begin{eqnarray}I_1&=&I_2+I_3=\displaystyle \frac{ R_3I_3}{ R_2 }+I_3\\&=&I_3\left(1+\frac{ R_3}{ R_2 }\right)… (2)’\end{eqnarray}$
(2)’式を(3)式に代入する
$\begin{eqnarray}R_1&=&\displaystyle \frac{ E-I_3R_3}{ I_3\left(1+\frac{ R_3}{ R_2 }\right) }\\\\&=&\displaystyle \frac{ R_2E-R_2R_3I_3}{ R_2I_3+R_3I_3}\\\\&=&\displaystyle \frac{ R_2R_3\left( \frac{E}{R_3}-I_3\right)}{ (R_2+R_3)I_3}\\\\&=&\displaystyle \frac{R_2R_3}{R_2+R_3}\left(\frac{E-I_3R_3}{I_3R_3}\right)\\\\&=&\displaystyle \frac{R_2R_3}{R_2+R_3}\left(\frac{E}{I_3R_3}-1\right)\end{eqnarray}$
答え (5)
2008年(平成20年)問6【電験理論の過去問題】
図のように、抵抗、切換スイッチS及び電流計を接続した回路がある。この回路に直流電圧 100[V]を加えた状態で、図のようにスイッチSを開いたとき電流計の指示値は 2.0[A]であった。また、スイッチSを①側に閉じたとき電流計の指示値は 2.5[A]、スイッチSを②側に閉じたとき電流計の指示値は 5.0[A]であった。このとき抵抗 $r$[Ω]の値として、正しいのは次のうちどれか。
ただし、電流計の内部抵抗は無視できるものとし、測定誤差はないものとする。
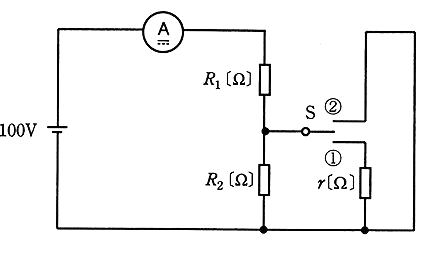
(1) 20 (2) 30 (3) 40 (4) 50 (5) 60
スイッチSを開いているときの回路の式は
$2.0×(R1+R2)=100$
$R_1+R_2=50$ … (1)
スイッチSを①側に閉じたときの回路の式は
$2.5\left(R_1+\displaystyle \frac{ rR_2}{ r+R_2 }\right)=100$
$R_1+\displaystyle \frac{ rR_2}{ r+R_2 }=40$ … (2)
スイッチSを②側に閉じたとき、$R_2$は短絡します。回路の式は
$5.0×R_1=100$
$R_1=20$ … (3)
(3)式を(1)式に代入します。
$R_2=50-20=30$ … (4)
(3)、(4)式を(2)式に代入します。
$20+\displaystyle \frac{30r}{30+r}=40$
$\displaystyle \frac{30r}{30+r}=20$
$30r=20(30+r)$
$r=60$ [Ω]
答え (5)
2009年(平成21年)問6【電験理論の過去問題】
抵抗値が異なる抵抗 $R_1$[Ω]と $R_2$[Ω]を図1のように直列に接続し、30[V]の直流電圧を加えたところ、回路に流れる電流は 6[A]であった。次にこの抵抗 $R_1$[Ω]と $R_2$[Ω]を図2のように並列に接続し、30[V]の直流電圧を加えたところ、回路に流れる電流は 25[A]であった。このとき $R_1$[Ω]、$R_2$[Ω]のうち小さいほうの抵抗[Ω]の値として、正しいのは次のうちどれか。
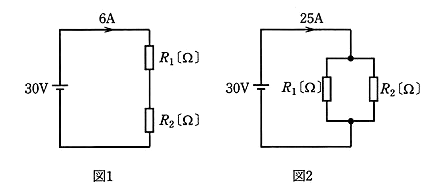
(1) 1 (2) 1.2 (3) 1.5 (4) 2 (5) 3
図1より
$6(R_1+R_2)=30$
$R_1+R_2=5$ … (1)
図2より
$25×\displaystyle \frac{ R_1R_2}{ R_1+R_2}=30$ … (2)
(1)式を(2)式に代入する
$25×\displaystyle \frac{ R_1R_2}{5}=30$
$R_1R_2=6$… (2)’
(1)式を変形し(2)’式に代入する
$(5-R_2)R_2=6$
$R_2^2-5R_2+6=0$
$(R_2-2)(R_2-3)=0$
$R_2=2,3$
よって小さいほうの抵抗は 2[Ω]になります。
答え (4)
2012年(平成24年)問6【電験理論の過去問題】
図のように、抵抗を直並列に接続した回路がある。この回路において、$I_1=100$[mA]のとき、$I_4$ [mA]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
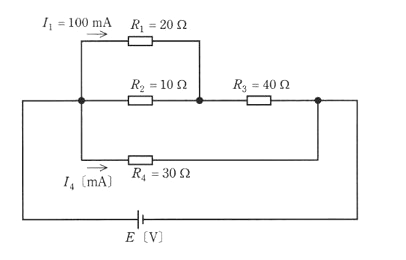
(1) 266 (2) 400 (3) 433 (4) 467 (5) 533
抵抗 $R_2$ に流れる電流を $I_2$[A]、抵抗 $R_3$ に流れる電流を $I_3$[A]とします。
抵抗 $R_1$ の電圧降下は $20×0.1=2$[V]、抵抗 $R_2$ の電圧降下は $R_1$ の電圧降下と同じで、$2$[V]となりますので、
$I_2=\displaystyle \frac{ 2}{ R_2}=\displaystyle \frac{ 2}{ 10}=0.2$[A]
$I_3=I_1+I_2=0.1+0.2=0.3$[A]
抵抗 $R_3$ の電圧降下は $40×0.3=12$[V]、抵抗 $R_4$ の電圧降下は $2+12=14$[V] となりますので、
$I_4=\displaystyle \frac{ 14}{ R_4}=\displaystyle \frac{ 14}{ 30}=0.467$[A]
答え (4)
2013年(平成25年)問5【電験理論の過去問題】
図のように、抵抗 $R$[Ω]と抵抗 $R_x$[Ω]を並列に接続した回路がある。この回路に直流電圧 $V$[V] を加えたところ、電流 $I$[A]が流れた。$R_x$[Ω]の値を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
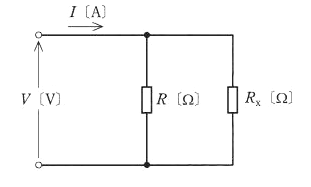
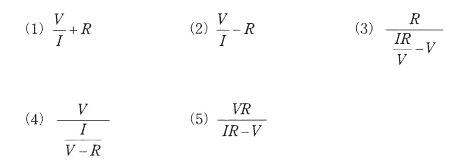
回路の合成抵抗を $R’$ とすると
$R’=\displaystyle \frac{ RR_x}{ R+Rx}$
オームの法則より
$V=I×\displaystyle \frac{ RR_x}{ R+Rx}$
この式を $Rx$ について解いていきます。
$V(R+R_x)=IRR_X$
$VR=Rx(IR-V)$
$Rx=\displaystyle \frac{ VR}{ IR-V}$
答え (5)
2013年(平成25年)問8【電験理論の過去問題】
図に示すような抵抗の直並列回路がある。この回路に直流電圧 5[V]を加えたとき、電源から流れ出る電流 $I$[A]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
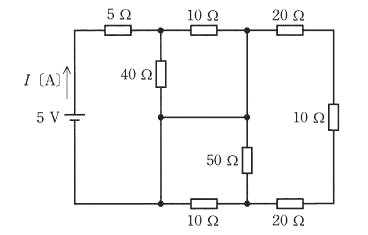
(1) 0.2 (2) 0.4 (3) 0.6 (4) 0.8 (5) 1.0
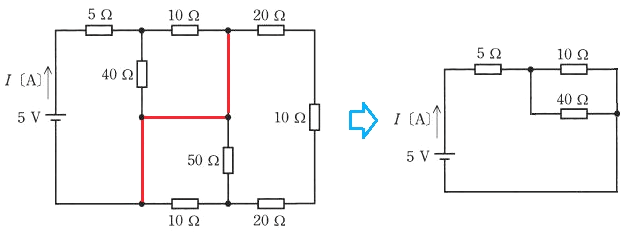
上図左の赤線部は短絡していますので、上右図のように書き換えることができます。
合成抵抗を$R$とすると
$R=5+\displaystyle \frac{ 10×40}{10+40}=13$[Ω]
オームの法則より
$5=13I I=0.38≒0.4$[A]
答え (2)
2014年(平成26年)問6【電験理論の過去問題】
図のように、抵抗を直並列に接続した直流回路がある。この回路を流れる電流 $I$ の値は、$I=10 mA$ であった。このとき、抵抗 $R_2$[kΩ]として、最も近い $R_2$ の値を次の(1)~(5)のうちから一つ選べ。
ただし抵抗 $R_1$[kΩ]に流れる電流 $I_1$[mA]と抵抗 $R_2$[kΩ]に流れる電流 $I_2$[mA]の電流比 $\displaystyle \frac{ I_1}{I_2} $ の値は $\displaystyle \frac{ 1}{2} $ とする。
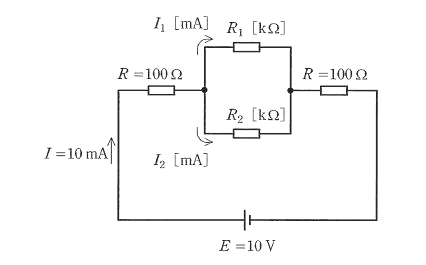
(1) 0.3 (2) 0.6 (3) 1.2 (4) 2.4 (5) 4.8
抵抗 $R_1$ の電圧降下と抵抗 $R_2$ の電圧降下は等しいので、
$R_1I_1=R_2I_2$
$\displaystyle \frac{ I_1}{I_2} =\displaystyle \frac{ 1}{2} $ なので、
$R_1=2R_2$
$R1$ と $R2$ の合成抵抗は、
$\displaystyle \frac{R_1R_2}{R_1+R_2} =\displaystyle \frac{2R_2R_2}{2R_2+R_2} =\displaystyle \frac{2R_2}{3}$ [kΩ]
オームの法則より、回路の合成抵抗は $\displaystyle \frac{10[V]}{10[mA]} =1$[kΩ]ですので、
$1=0.2+\displaystyle \frac{2R_2}{3}$
$R_2=1.2$[kΩ]
答え (3)
2015年(平成27年)問4【電験理論の過去問題】
図のような直流回路において、直流電源の電圧が 90Vであるとき、抵抗 $R_1$[Ω],$R_2$[Ω],$R_3$[Ω]の両端電圧はそれぞれ 30V,15V,10V であった。抵抗 $R_1$,$R_2$,$R_3$ のそれぞれの値[Ω]の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
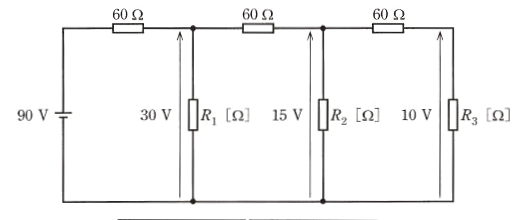
わかるところから順次、電圧と電流を計算していきます。
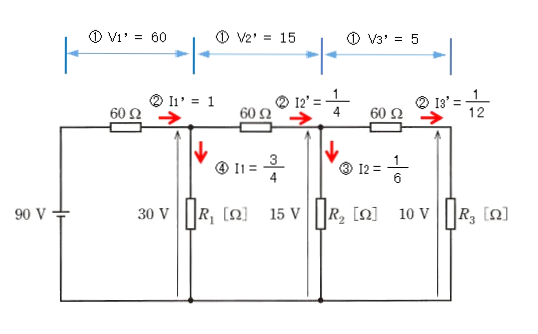
- $V_1’=90-30=60$
$V_2’=30-15=15$
$V_3’=15-10=5$
- $60I_1’=60 I_1’=1$
$60I_2’=15 I_2’=\displaystyle\frac{ 1}{4}$
$60I_3’=5 I_3’=\displaystyle\frac{ 1}{12}$
- $I_2’=I_2+I_3’$
$\displaystyle\frac{ 1}{4}=I_2+\displaystyle\frac{ 1}{12}$
$I_2=\displaystyle\frac{ 1}{6}$
- $I_1’=I_1+I_2’$
$1=I_1+\displaystyle\frac{ 1}{4}$
$I_1=\displaystyle\frac{ 3}{4}$
よって
$R1×\displaystyle\frac{ 3}{4}=30 R1=40$[Ω]
$R2×\displaystyle\frac{ 1}{6}=15 R2=90$[Ω]
$R3×\displaystyle\frac{ 1}{12}=10 R3=120$[Ω]
答え (5)
2017年(平成29年)問5【電験理論の過去問題】
図のように直流電源と4個の抵抗からなる回路がある。この回路において $20Ω$ の抵抗に流れる電流 $I$ の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
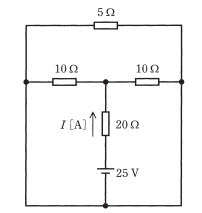
(1) 0.5 (2) 0.8 (3) 1.0 (4) 1.2 (5) 1.5
下図のA点とB点に注目すると、A点,B点共に電源間に抵抗がありませんので、電流は全て電源側に流れ、5Ωの抵抗のある回路には電流は流れません。
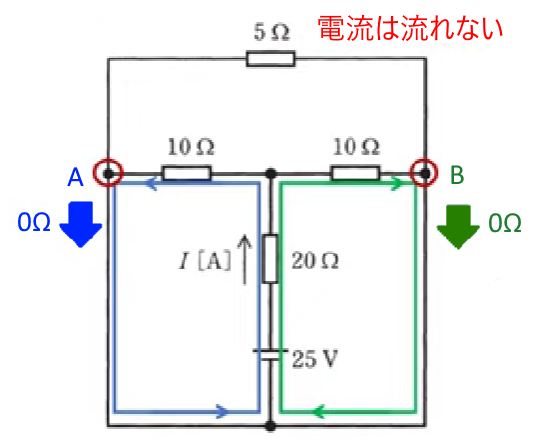
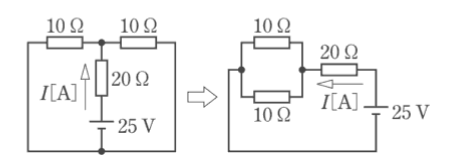
等価回路で表すと次の下図になります。等価回路より回路の合成抵抗 $R$[Ω]は、
$R=\displaystyle\frac{10×10}{10+10}+20=25$[Ω]
したがって、$20Ω$ の抵抗に流れる電流 $I$ の値[A]は、
$I=\displaystyle\frac{25}{25}=1.0$[A]
答え(3)
2017年(平成29年)問7【電験理論の過去問題】
次の文章は、直流回路に関する記述である。
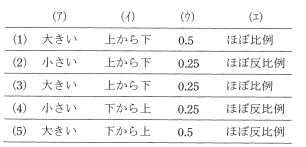
図の回路において、電流の値 $I$[A]は $4A$ よりも( ア )。このとき、抵抗 $R_1$ の中で動く電子の流れる向きは図の( イ )であり、電界の向きを併せて考えると、電気エネルギーが失われることになる。また、$0.25s$ の間に電源が供給する電力量に対し、同じ時間に抵抗 $R_1$ が消費する電力量の比は( ウ )である。抵抗は、消費した電力量だけの熱を発生することで温度が上昇するが、一方で、周囲との温度差に( エ )する熱を放出する。
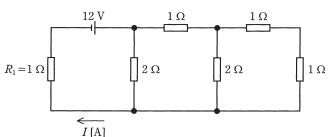
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
回路の合成抵抗を求めると、下図のようになります。
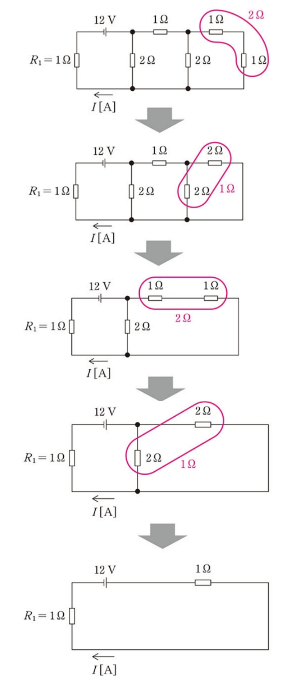
したがって、電流の値 $I$[A]は、$I=\displaystyle\frac{E}{R}=\displaystyle\frac{12}{2}=6$[A]ですので、(ア)の答えは、「大きい」となります。
電子の流れる向きは電流の流れる向きと逆方向になりますので、(イ)の答えは「上から下」になります。
$0.25s$ の間に電源が供給する電力量 $W$ に対し、抵抗 $R_1$ が消費する電力量 $W_R$ の比は
$W=VIt=12×6×0.25=18$
$W_R=R_1I^2t=1×6^2×0.25=9$
$\displaystyle\frac{W_R}{W}=\displaystyle\frac{9}{18}=0.5$ … (ウ)
抵抗は、消費した電力量だけの熱を発生することで温度が上昇するが、一方で、周囲との温度差に( ほぼ比例 )する熱を放出する。
答え(1)
2018年(平成30年)問6【電験理論の過去問題】
Ra、Rb 及び Rc の三つの抵抗器がある。これら三つの抵抗器から二つの抵抗器( R1 及び R2 )を選び、図のように、直流電流計及び電圧 $E=1.4$Vの直流電源を接続し、次のような実験を行った。
- 実験Ⅰ:R1 を Ra、R2 を Rb としたとき、電流 $I$ の値は 56mA であった。
- 実験Ⅱ:R1 を Rb、R2 を Rc としたとき、電流 $I$ の値は 35mA であった。
- 実験Ⅲ:R1 を Ra、R2 を Rc としたとき、電流 $I$ の値は 40mA であった。
これらのことから、Rb の抵抗値[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、直流電源及び直流電流計の内部抵抗は無視できるものとする。
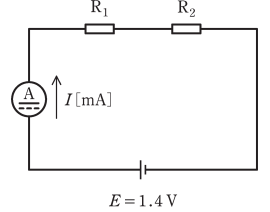
(1) 10 (2) 15 (3) 20 (4) 25 (5) 30
実験Ⅰ~Ⅲを、オームの法則 $R=\displaystyle\frac{E}{I}$ に代入します。
実験Ⅰ:$R_a+R_b=\displaystyle\frac{1.4}{0.056}=25$
実験Ⅱ:$R_b+R_c=\displaystyle\frac{1.4}{0.035}=40$
実験Ⅲ:$R_a+R_c=\displaystyle\frac{1.4}{0.04}=35$
実験Ⅰ~Ⅲで導き出した、連立方程式から $R_b$ を求めます。
3つの式を足し合わせます。
$R_a+R_b+R_b+R_c+R_a+R_c=25+40+35$
$R_a+R_b+R_c=50$
実験Ⅲの式 $R_a+R_c=35$ ですので、
$R_a+R_c+R_b=50$
$35+R_b=50$
$R_b=15$
答え(2)
電験三種の理論科目に出題される「直流分野」のページ
1.直流回路の基本問題
2.ホイートストンブリッジ回路
3.キルヒホッフの法則と不平衡ブリッジ回路
4.回路計算の定理(重ね合わせ・テブナン)
5.直流回路の消費電力






