第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「三相同期発電機の出力と並行運転」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「三相同期発電機の出力と並行運転」の過去問題も解説しています。
三相同期発電機の出力
同期インピーダンスは、$\dot{Z_s}=r_a+jx_s$ ですが、一般に $x_s$[Ω]は $r_a$[Ω]に比べて非常に大きいので、$x_s$ に対して $r_a$ を無視することができます。そのときの三相同期発電機1相分の等価回路を図1(a)に示し、そのベクトル図を図(b)に示します。
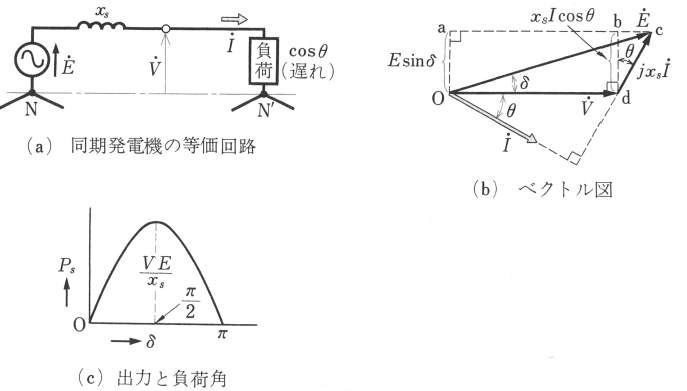
三相同期発電機の1相分の出力を $P_s$[W]とすると、
$P_s=VIcos θ$ … (1)
と表わすことができ、図(b)より、$x_sIcosθ=Esinδ$ となります。この式の両辺に $\displaystyle\frac{V}{x_s}$ を掛けると、$P_s=VIcosθ=\displaystyle\frac{VE}{x_s}sinδ$ となります。したがって、 3相の合計出力 $P$ は次のようになります。
$P=3P_s=\displaystyle\frac{3VE}{x_s}sinδ$ … (2)
つまり、供給電圧 $\dot{V}$ 、誘導起電力 $\dot{E}$ および同期リアクタンス $x_s$ が一定なら、図(c)に示すように出力 $P_s$ は $V$ に対する $E$ の位相角 $δ$ の正弦関数で表されます。この $δ$ を負荷角といいます。
なお、発電機が負荷に電力を送るには、$δ$ は正、すなわち $\dot{E}$ は $\dot{V}$ より位相が進んでいなくてはなりません。しかし、$E$ の大きさは必ずしも $V$ より大きくなくてもいいです。
同期発電機の出力を求める公式
$P=3VIcosθ=\displaystyle\frac{3VE}{x_s}sinδ$
$P$[W]:三相同期発電機の出力
$I$[A]:負荷電流
$V$[V]:端子電圧
$E$[V]:誘導起電力
$δ$:負荷角
三相同期発電機の並行運転
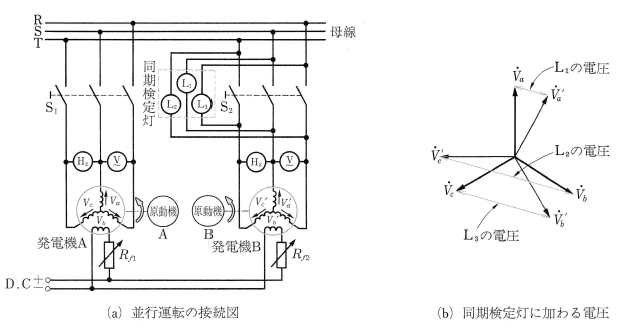
2台以上の同期発電機を、一つの母線に並列に接続して運転することを並行運転といいます。図2の母線 R,S,T は2台の発電機A,Bと共通に接続されています。
並列接続
図2(a)に示すように、すでに同期発電機AがスイッチS1を閉じて母線に接続して運転されているとき、同じ母線に同期発電機Bを並列に接続するには、次の条件が必要です。
- 同期発電機A,Bの起電力の周波数が等しい。
- A,Bの起電力の大きさが等しい。
- A,Bの起電力の位相が一致している。
- 起電力の波形が等しい。
ポイントの4番以外の三つの条件を満たすには、次のような操作を行います。
- 周波数を等しくするには、原動機Bの回転速度を調整する。
- 起電力の大きさを等しくするには、原動機Bの界磁抵抗 $R_{f2}$[Ω]を加減し、磁極の励磁を調整する。
- 起電力の位相を一致させるためには、原動機 Bの回転速度を調整する。
起電力の位相が一致しているかどうかは、図2(a)の同期検定灯といわれるランプ L1,L2,L3 の明るさから判断します。図(b)のベクトル図から、位相を一致させるとランプ L1 が消え、L2,L3 は同じ明るさになります。このようにして、三つの条件が整ったとき、スイッチS2を閉じて、同期発電機Bを並列に接続し、並行運転ができます。
無効横流
図3のように、起電力 $\dot{E_1}$[V],$\dot{E_2}$[V]をもつ同期発電機A,Bが母線に接続され、並行運転を行っています。
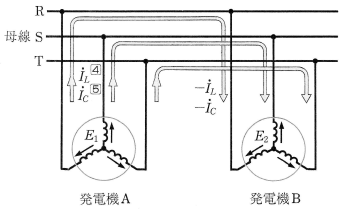
発電機A・Bの同期インピーダンス $\dot{Z_s}$[Ω]が等しい場合は、通常、起電力が等しく、$\dot{E_1}=\dot{E_2}$ で運転されています。
いま、発電機の励磁が変化して、$\dot{E_1}>\dot{E_2}$ となったとき、$\dot{E_1}-\dot{E_2}=\dot{E_{12}}$ の差の電圧によって、
$\dot{I_L}=\displaystyle\frac{\dot{E_{12}}}{2\dot{Z_s}}=\displaystyle\frac{\dot{E_{12}}}{2(r_a+jx_s)}$[A]
の電流が図3のように、両発電機間に循環します。
同期インピーダンス $\dot{Z_s}$ はほとんどが同期リアクタンスであり、図4のベクトル図のように、発電機Aから流出する $\dot{I_L}$ は $\dot{E_1}$ に対して $\displaystyle\frac{π}{2}$[rad]遅れた電流になり、$\dot{E_2}$ に対しては流入する電流になって $-\dot{I_L}$ となり、 $\displaystyle\frac{π}{2}$[rad]進んだ電流になります。その結果、発電機Aでは、電機子反作用の減磁作用が生じて $\dot{E_1}$ を低下させ、発電機Bでは増磁作用が生じて $\dot{E_2}$ を上昇させ、両発電機の起電力が等しくなるように作用します。
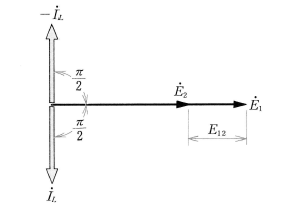
$\dot{I_L}$ は両発電機間を循環し、$\dot{E_1}$,$\dot{E_2}$ に対してほぼ $\displaystyle\frac{π}{2}$[rad]の位相差をもっているので、「無効横流」とよびます。これは出力には無関係で、両発電機の力率を変化させ、電機子巻線に抵抗損を生じさせ、巻線を加熱させる原因になっています。
有効横流
同期発電機A,Bが並行運転をしているとき、発電機Aを駆動している原動機の出力を上げると、図5のベクトル図のように、発電機Bより早く回転しようとして $\dot{E_1}$ の位相が $\dot{E_2}$ の位相よりも $δ$[rad]進みます。
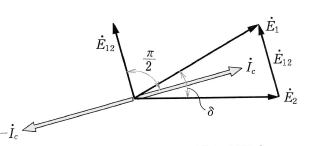
そのため、$\dot{E_1}-\dot{E_2}=\dot{E_{12}}$ の差の電圧が発生し、両発電機の同期インピーダンス $\dot{Z_s}$[Ω]が等しいとすると、$\dot{I_c}=\displaystyle\frac{\dot{E_{12}}}{2\dot{Z_s}}$[A]の電流が発電機Aより流れます。
この $\dot{I_c}$[A]は $\dot{E_{12}}$ より $\displaystyle\frac{π}{2}$[rad]遅れ、$\dot{E_1}$ とほぼ同相になって、発電機Aは $\dot{E_1},\dot{I_c}$ の出力を増やし、回転の上昇が抑制されます。また、発電機Bの $-\dot{I_c}$ は $\dot{E_2}$ より $π$[rad]の位相差があり、$\dot{E_2},(-\dot{I_c})$ の出力を減少し、そのため回転が上昇して、$\dot{E_1}$ と $\dot{E_2}$ が同位相になります。
この電流 $\dot{I_c}$ を「有効横流」とよんで、位相が進んだ発電機から位相の遅れた発電機へ電力を供給する作用を行っています。
負荷分担
同期発電機Aから同期発電機Bへ負荷電流の分担を変えるには、次のような操作を行います。
- Aの励磁を弱め、Bの励磁を強めて、しだいに無効横流の分担をBに移す。
- Aの回転速度を遅くし、Bの回転速度を速めると、負荷の有効横流の分担はしだいにBに移る。
- (1)と(2)の操作を交互に行って、負荷の移動を行い、分担を変える。
電験三種-機械の過去問解説:三相同期発電機の出力と並行運転
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
2001年(平成13年)問4
回転速度 600[min-1]で運転している極数 12 の同期発電機がある。この発電機に極数 8 の同期発電機を並行運転させる場合、極数 8 の発電機の回転速度[min-1]の値として、正しいのは次のうちどれか。
(1) 400 (2) 450 (3) 600 (4) 900 (5) 1200
2001年(平成13年)問4 過去問解説
並行運転させる場合、 同期発電機の起電力の周波数を合わせなければなりません。 回転速度 600[min-1]で運転している極数 12 の同期発電機で考えると、
同期速度 $N_s=\displaystyle\frac{120×f(周波数)}{p(極数)}$ より、
$600=\displaystyle\frac{120×f}{12}$
$f=60$[Hz]
極数 8 の同期発電機が、$f=60$[Hz]のときの同期速度 $N_s$ は、
$N_s=\displaystyle\frac{120×60}{8}=900$[min-1]
答え (4)
2009年(平成21年)問4
同期発電機を商用電源(電力系統)に遮断器を介して接続するためには、同期発電機の( ア )の大きさ、( イ ) および位相が商用電源のそれらと一致していなければならない。同期発電機の商用電源への接続に際しては、これらの条件が一つでも満足されていなければ、遮断器を投入したときに過大な電流が流れることがあり、場合によっては同期発電機が損傷する。仮に、( ア )の大きさ、( イ ) が一致したとしても、位相が異なる場合には位相差による電流が生じる。同期発電機が無負荷のとき、この電流が最大となるのは位相差が( ウ )[°]のときである。
同期発電機の( ア )の大きさ、( イ )および位相を商用電源のそれらと一致させるには、( エ )及び調速装置を用いて調整する。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはめる語句又は数値として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | インピーダンス | 周波数 | 60 | 誘導調整装器 |
| (2) | 電圧 | 回転速度 | 60 | 電圧調整装置 |
| (3) | 電圧 | 周波数 | 60 | 誘導調整装器 |
| (4) | インピーダンス | 周波数 | 180 | 電圧調整装置 |
| (5) | 電圧 | 周波数 | 180 | 電圧調整装置 |
2009年(平成21年)問4 過去問解説
同期発電機を商用電源(電力系統)に遮断器を介して接続するためには、同期発電機の( 電圧 )の大きさ、( 周波数 ) および位相が商用電源のそれらと一致していなければならない。同期発電機の商用電源への接続に際しては、これらの条件が一つでも満足されていなければ、遮断器を投入したときに過大な電流が流れることがあり、場合によっては同期発電機が損傷する。仮に、( 電圧 )の大きさ、( 周波数 ) が一致したとしても、位相が異なる場合には位相差による電流が生じる。同期発電機が無負荷のとき、この電流が最大となるのは位相差が( 180 )[°]のときである。
同期発電機の( 電圧 )の大きさ、( 周波数 )および位相を商用電源のそれらと一致させるには、( 電圧調整装置 )及び調速装置を用いて調整する。
答え (5)
2010年(平成22年)問15
1相あたりの同期リアクタンスが 1[Ω]の三相同期発電機が無負荷電圧 346[V](相電圧 200[V])を発生している。そこに抵抗器負荷を接続すると電圧が 300[V](相電圧 173[V])に低下した。次の(a)及び(b)に答えよ。
ただし、三相同期発電機の回転速度は一定で、損失は無視するものとする。
(a) 電機子電流[A]の値として、最も近いのは次のうちどれか。
(1) 27 (2) 70 (3) 100 (4) 150 (5) 173
(b) 出力[kW]の値として、最も近いのは次のうちどれか。
(1) 24 (2) 30 (3) 52 (4) 60 (5) 156
2010年(平成22年)問15 過去問解説
(a) 三相同期発電機の1相分の等価回路とベクトル図を示します。
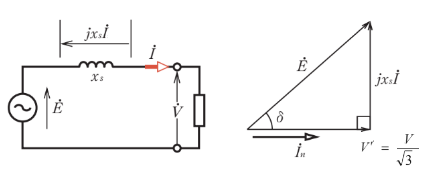
相電圧 $V_p$[V]は、抵抗器負荷を接続すると 200[V]から 173[V]に低下したので、同期リアクタンスを $x_s$[Ω]、 電機子電流を $I$[A]とすると、ベクトル図より、
$E^2=(\displaystyle\frac{V}{\sqrt{3}})^2+(x_sI)^2$
$(1×I)=\sqrt{E^2- (\displaystyle\frac{V}{\sqrt{3}})^2 }=\sqrt{200^2- (\displaystyle\frac{300}{\sqrt{3}})^2 }=100 $
$I=100$[A]
答え (3)
(b) 力率は記載がないので、100% と考えます。
$P=\sqrt{3}VIcosθ= \sqrt{3}×300×100×1=52$[kW]
答え (3)
2017年(平成29年)問4
次の文章は、三相同期発電機の並行運転に関する記述である。
既に同期発電機Aが母線に接続されて運転しているとき、同じ母線に同期発電機Bを並列に接続するために必要な条件又は操作として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- 母線電圧と同期発電機Bの端子電圧の相回転方向が一致していること。同期発電機Bの設置後又は改修後の最初の運転時に相回転方向の一致を確認すれば、その後は母線への並列のたびに相回転方向を確認する必要はない。
- 母線電圧と同期発電機Bの端子電圧の位相を合わせるために、同期発電機Bの駆動機の回転速度を調整する。
- 母線電圧と同期発電機Bの端子電圧の大きさを等しくするために、同期発電機Bの励磁電流の大きさを調整する。
- 母線電圧と同期発電機Bの端子電圧の波形をほぼ等しくするために、同期発電機Bの励磁電流の大きさを変えずに励磁電圧の大きさを調整する。
- 母線電圧と同期発電機Bの端子電圧の位相の一致を検出するために、同期検定器を使用するのが一般的であり、位相が一致したところで母線に並列する遮断器を閉路する。
2017年(平成29年)問4 過去問解説
並列運転の条件は、
- 同期発電機A,Bの起電力の周波数が等しい。
- A,Bの起電力の大きさが等しい。
- A,Bの起電力の位相が一致している。
- 起電力の波形が等しい。
(4)の記述「母線電圧と同期発電機Bの端子電圧の波形をほぼ等しくするために、同期発電機Bの励磁電流の大きさを変えずに励磁電圧の大きさを調整する。」は、 励磁電流の大きさを調整すると、電圧の大きさも変わりますので、この記述は誤りです。
答え (4)
電験三種の機械科目に出題される「同期機」のページ
- 三相同期発電機の原理と構造
- 三相同期発電機の等価回路
- 三相同期発電機の特性
- 三相同期発電機の出力と並行運転
- 三相同期電動機の原理と特性
- 三相同期電動機の始動方法






