第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される三相交流回路について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された三相交流回路の過去問題も解説しています。
三相交流の瞬時値
磁界の中でコイルを回転させると、正弦波交流が発生します。このときコイルを 120°($=\displaystyle \frac{ 2}{ 3 }π$)ずつずらして回転させると、同じ周波数で3つの正弦波交流が発生します。

この3つの起電力の瞬時値を $e_a$,$e_b$,$e_c$ とし、$e_a$ を基準にとり、$t=0$ のときの位相角を $0$ とすると、各相の起電力は次のように表すことができます。
$e_a=\sqrt{2}Esinωt$
$e_b=\sqrt{2}Esin(ωt-\displaystyle \frac{ 2}{ 3 }π)$
$e_c=\sqrt{2}Esin(ωt-\displaystyle \frac{ 4}{ 3 }π)$
このように、3つの相の角速度 $ω$ が同じで、位相の違う起電力を1つのものとして取り扱う場合を「三相交流」といいます。周波数が等しく、位相の異なる3個の起電力を含む回路といえます。尚、おのおのの最大値が等しく、位相が互いに 120°ずつ異なるものを特に対称三相交流といいます。対称三相交流では、どの時刻においても、各交流の大きさの和は $0$ になります。つまり、瞬時値 $e_a$,$e_b$,$e_c$ の和は $0$ になります。
$e_a+e_b+e_c=0$
三相交流のベクトル表示と複素数表示
三相交流の各相の瞬時値 $e_a$,$e_b$,$e_c$ をベクトル $\dot{ E _a}$,$\dot{ E _b}$,$\dot{ E _c}$ で表すと次のようになります。尚、$\dot{ E _a}$ を基準に考えています。
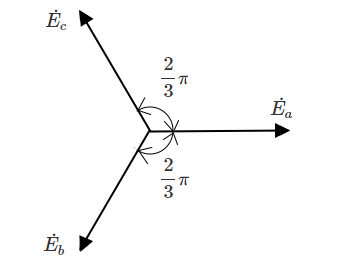
$\dot{ E _a}=E∠0$
$\dot{ E _b}=E∠-\displaystyle \frac{ 2}{ 3 }π$
$\dot{ E _c}=E∠-\displaystyle \frac{ 4}{ 3 }π$
複素数表示では、次のように表すことができます。
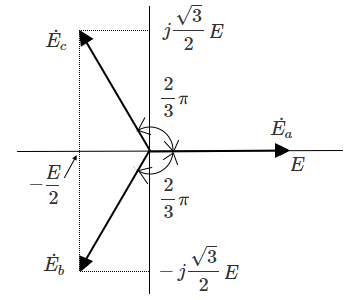
$\begin{eqnarray}\dot{ E _a}&=&E∠0\\&=&E(cos0+jsin0)\\&=&E\end{eqnarray}$
$\begin{eqnarray}\dot{ E _b}&=&E∠-\displaystyle \frac{ 2}{ 3 }π\\&=&E(cos(-\displaystyle \frac{ 2}{ 3 }π)+jsin(-\displaystyle \frac{ 2}{ 3 }π))\\&=&E(-\displaystyle \frac{ 1}{ 2 }-j\displaystyle \frac{ \sqrt{3}}{ 2 })\end{eqnarray}$
$\begin{eqnarray}\dot{ E _c}&=&E∠-\displaystyle \frac{ 4}{ 3 }π\\&=&E(cos(-\displaystyle \frac{ 4}{ 3 }π)+jsin(-\displaystyle \frac{ 4}{ 3 }π))\\&=&E(-\displaystyle \frac{ 1}{ 2 }+j\displaystyle \frac{ \sqrt{3}}{ 2 })\end{eqnarray}$
対称三相交流では、どの時刻においても、各交流の大きさの和は $0$ になります。このことは、次のように計算で確認することができます。
$\begin{eqnarray}\dot{ E _a}+\dot{ E _b}+\dot{ E _c}&=&E+E(-\displaystyle \frac{ 1}{ 2 }-j\displaystyle \frac{ \sqrt{3}}{ 2 })+E(-\displaystyle \frac{ 1}{ 2 }+j\displaystyle \frac{ \sqrt{3}}{ 2 })\\&=&E-\displaystyle \frac{ 1}{ 2 }E-\displaystyle \frac{ 1}{ 2 }E+E(-j\displaystyle \frac{ \sqrt{3}}{ 2 }+j\displaystyle \frac{ \sqrt{3}}{ 2 })\\&=&0\end{eqnarray}$
電流も同様に、大きさの和は $0$ になります。
三相交流回路の結線方式
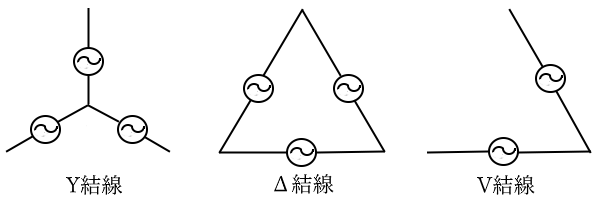
三相交流の電源の接続方法には、単相電源を3個接続した「Y(スター)結線」と「Δ(デルタ)結線」があります。また、単相電源2個を接続して三相交流を発生させる「V(ブイ)結線」があります。
3個の電源の電圧の大きさが等しく、3個の位相が $=\displaystyle \frac{ 2}{ 3 }π$ ずつずれているものを
「対称三相交流」といいます。また、そうでないものを「非対称三相交流」といいます。
三相交流の負荷の接続方法にもY結線とΔ結線 があります。
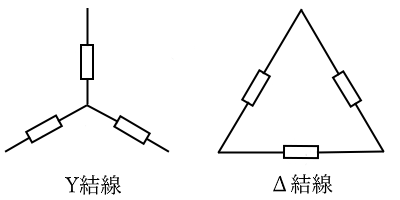
3個の負荷の大きさが等しいものを「平衡三相負荷」といいます。
相電圧と線間電圧
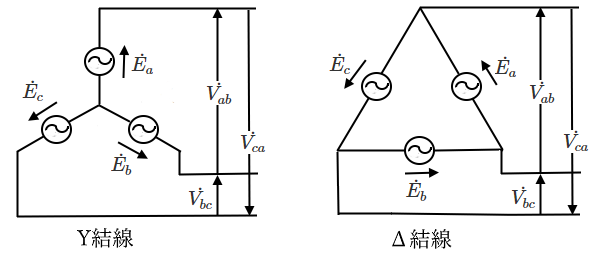
図のような三相電源において、$\dot{ E _a}$,$\dot{ E _b}$,$\dot{ E _c}$ を「相電圧」、 $\dot{ V_{ab}}$,$\dot{ V_{bc}}$,$\dot{ V_{ca}}$ を「線間電圧」といいます。対称三相交流では、 各相電圧の大きさと各線間電圧の大きさが等しくなります。
相電流と線電流
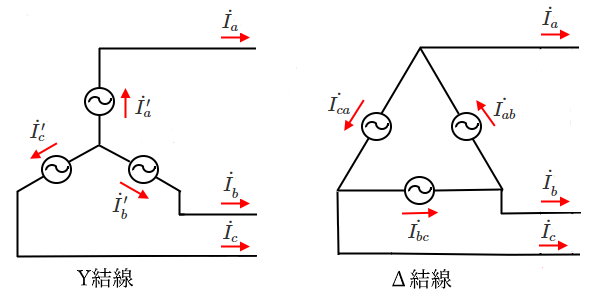
Y結線の $\dot{ I_a’}$,$\dot{ I_b’}$,$\dot{ I c’}$ とΔ結線の $\dot{ I_{ab}}$,$\dot{ I_{bc}}$,$\dot{ I_{ca}}$ を「相電流」、$\dot{ I_a}$,$\dot{ I_b}$,$\dot{ I_c}$ を「線電流」といいます。対称三相交流では、 各相電流の大きさと各線電流の大きさが等しくなります。
Y結線の電源とY結線の負荷を接続した回路
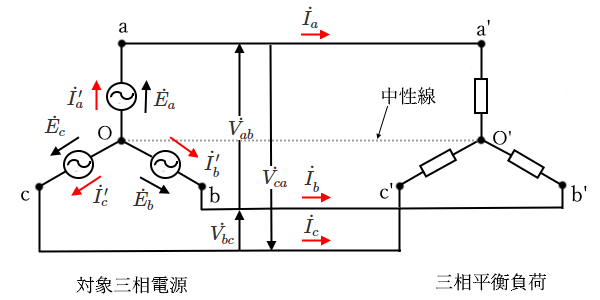
次の図のように電源がY結線、負荷がY結線された回路を考えます。電源の O 点と負荷の O’ 点を中性点といい、 O 点と O’間を結ぶ線を中性線といいます。中性線を流れる電流は、各相の電流の和であり、平衡負荷の時は 0 となります。そのため、取り外しても全体の回路の電流分布には変化がありませんので、省略できます。このときは、単相交流回路が3つあるものとして考えることができます。
単相交流として見ると、Y-Y回路は電源とインピーダンスの直列回路になりますので、「線電流 = 相電流 」になります。
$\dot{ I_a}=\dot{ I_a’}$ , $\dot{ I_b}=\dot{ I_b’}$ , $\dot{ I_c}=\dot{ I_c’}$
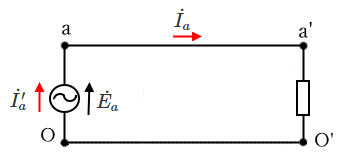
また、電源側に注目してみます。相電圧($\dot{ E _a}$,$\dot{ E_b}$,$\dot{ E _c}$)と線間電圧($\dot{ V_{ab}}$,$\dot{ V_{bc}}$,$\dot{ V_{ca}}$ )の関係は次のようになります。
$\dot{ V_{ab}}=\dot{ E _a}-\dot{ E _b}$
$\dot{ V_{bc}}=\dot{ E _b}-\dot{ E _c}$
$\dot{ V_{ca}}=\dot{ E _c}-\dot{ E _a}$
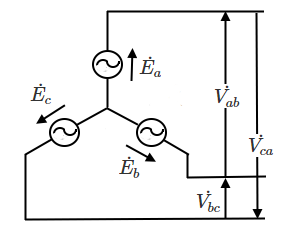
相電圧 $\dot{ E _a}$ を基準にしたベクトル図で、$\dot{ V_{ab}}=\dot{ E _a}-\dot{ E _b}$ を表します。
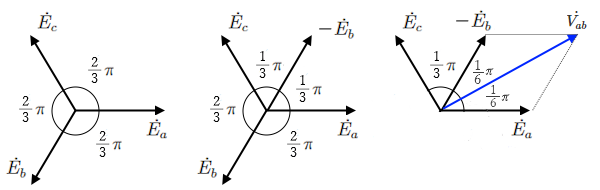
ベクトル図より、 線間電圧 $\dot{ V_{ab}}$ と、相電圧 $\dot{ E _a}$ に $\displaystyle \frac{ π}{ 6 }$ の位相差があることがわかります。これは、三相とも同じことが言え、Y-Y回路では「線間電圧は相電圧より $\displaystyle \frac{ π}{ 6 }$ 進み」になります。
次に、線間電圧 $\dot{ V_{ab}}$ の大きさを求めます。ベクトル図より、$\dot{ V_{ab}}$ と $\dot{ E _a}$ から成る三角形は、2つの角度が $\displaystyle \frac{ π}{ 6 }$ の二等辺三角形ですので、点 a から 線分 $V_{ab}$ へ、下図のように垂線を下ろすと、辺の比が $1:2:\sqrt{3}$ の直角三角形が2つできます。
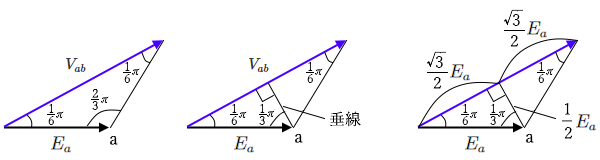
辺の比が $1:2:\sqrt{3}$ なので、線分 $V_{ab}$ の半分の長さは $\displaystyle \frac{\sqrt{3}}{ 2 }E_a$ になります。したがって、線分 $V_{ab}$ の長さは、$\sqrt{3}E_a$ になりますので、「線間電圧の大きさは相電圧の $\sqrt{3}$ 倍」になります。
$V_{ab}=\sqrt{3}E _a$ , $V_{bc}=\sqrt{3}E _b$ , $V_{ca}=\sqrt{3}E _c$
Y結線の電源とY結線の負荷を接続した回路のまとめ

相電圧:$\dot{ E_a}$,$\dot{ E _b}$,$\dot{ E _c}$
線間電圧:$\dot{ V_{ab}}$,$\dot{ V_{bc}}$,$\dot{ V_{ca}}$
相電流:$\dot{ I_a’}$,$\dot{ I_b’}$,$\dot{ I_c’}$
線電流:$\dot{ I_a}$,$\dot{ I_b}$,$\dot{ I_c}$
線電流 = 相電流
$\dot{ I_a}=\dot{ I_a’}$ , $\dot{ I_b}=\dot{ I_b’}$ , $\dot{ I_c}=\dot{ I_c’}$
線間電圧の大きさ = $\sqrt{3}$ 相電圧の大きさ
$V_{ab}=\sqrt{3}E_a$ , $V_{bc}=\sqrt{3}E_b$ , $V_{ca}=\sqrt{3}E _c$
線間電圧は相電圧より $\displaystyle \frac{ π}{ 6 }$ 進んでいる
$\dot{V_{ab}}=\sqrt{3}\dot{ E_a}∠\displaystyle \frac{ π}{ 6 }$ , $\dot{V_{bc}}=\sqrt{3}\dot{ E_b}∠\displaystyle \frac{ π}{ 6 }$ , $\dot{V_{ca}}=\sqrt{3}\dot{ E_c}∠\displaystyle \frac{ π}{ 6 }$
Δ結線の電源とΔ結線の負荷を接続した回路
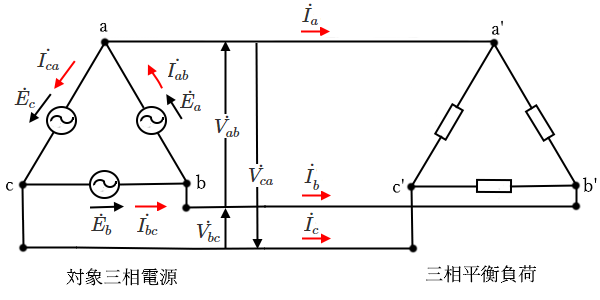
図のように電源がΔ結線、負荷がΔ結線された回路を考えます。Δ結線で接続された回路では、「線間電圧 = 相電圧」になります。
$\dot{ V_{ab}}=\dot{ E _a}$ , $\dot{ V_{bc}}=\dot{ E_b}$ , $\dot{ V_{ca}}=\dot{ E _c}$
ここで、電源側に注目してみます。線電流( $\dot{ I _a}$,$\dot{ I _b}$,$\dot{ I _c}$)と相電流($\dot{ I _{ab}}$,$\dot{ I _{bc}}$,$\dot{ I _{ca}}$ )の関係は次のようになります。
$ \dot{ I _a}=\dot{ I _{ab}}-\dot{ I _{ca}}$
$ \dot{ I _b}=\dot{ I _{bc}}-\dot{ I _{ab}}$
$ \dot{ I _c}=\dot{ I _{ca}}-\dot{ I _{bc}}$
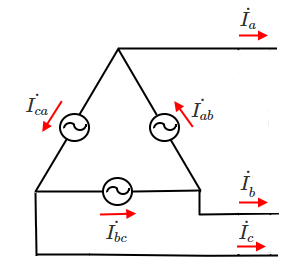
相電流 $\dot{ I _{ab}}$ を基準にしたベクトル図で、$ \dot{ I _a}=\dot{ I _{ab}}-\dot{ I _{ca}}$ を表します。
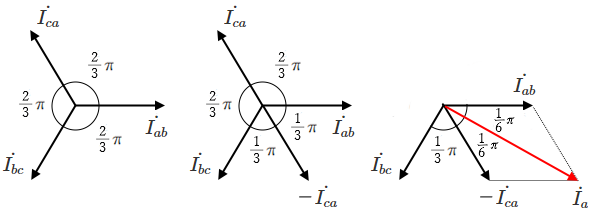
ベクトル図より、 線電流 $\dot{ I_{a}}$ と、相電流 $\dot{ I _{ab}}$ に $\displaystyle \frac{ π}{ 6 }$ の位相差があることがわかります。これは、三相とも同じことが言え、Y-Y回路では「線電流は相電流より $\displaystyle \frac{ π}{ 6 }$ 遅れ」になります。
次に、線電流 $\dot{ I _a}$ の大きさを求めます。ベクトル図より、$\dot{ I _a}$ と $\dot{ I_{ab}}$ から成る三角形は、2つの角度が $\displaystyle \frac{ π}{ 6 }$ の二等辺三角形ですので、点 a から 線分 $I_a$ へ、下図のように垂線を下ろすと、辺の比が $1:2:\sqrt{3}$ の直角三角形が2つできます。
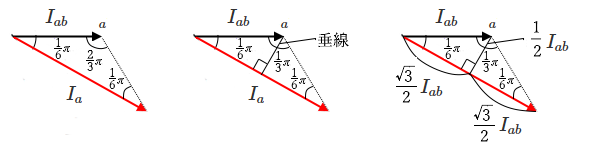
辺の比が $1:2:\sqrt{3}$ なので、線分 $I_{a}$ の半分の長さは $\displaystyle \frac{\sqrt{3}}{ 2 }I_{ab}$ になります。したがって、線分 $I_{a}$ の長さは、$\sqrt{3}I_{ab}$ になりますので、「線電流の大きさは相電流の $\sqrt{3}$ 倍」になります。
$I_{a}=\sqrt{3}I_{ab}$ , $I_{b}=\sqrt{3}I _{bc}$ , $I_{c}=\sqrt{3}I _{ca}$
Δ結線の電源とΔ結線の負荷を接続した回路のまとめ

相電圧:$\dot{ E_a}$,$\dot{ E _b}$,$\dot{ E _c}$
線間電圧:$\dot{ V_{ab}}$,$\dot{ V_{bc}}$,$\dot{ V_{ca}}$
相電流:$\dot{ I_{ab}}$,$\dot{ I_{bc}}$,$\dot{ I_{ca}}$
線電流:$\dot{ I_a}$,$\dot{ I_b}$,$\dot{ I_c}$
線電流の大きさ = $\sqrt{3}$ 相電流の大きさ
$I_{a}=\sqrt{3}I_{ab}$ , $I_{b}=\sqrt{3}I _{bc}$ , $I_{c}=\sqrt{3}I _{ca}$
線間電圧 = 相電圧
$\dot{ V_{ab}}=\dot{ E_a}$ , $\dot{ V_{bc}}=\dot{ E_b}$ , $\dot{ V_{ca}}=\dot{ E _c}$
線電流は相電流より $\displaystyle \frac{ π}{ 6 }$ 遅れている
$\dot{ I _a}=\sqrt{3}\dot{ I_{ab}}∠-\displaystyle \frac{ π}{ 6 }$ , $\dot{ I _b}=\sqrt{3}\dot{ I_{bc}}∠-\displaystyle \frac{ π}{ 6 }$ , $\dot{ I _c}=\sqrt{3}\dot{ I_{ca}}∠-\displaystyle \frac{ π}{ 6 }$
負荷の Y ー Δ の相互変換
三相回路で、電源と負荷の結線方法が異なる場合には、負荷側を Y ⇒ Δ または Δ ⇒ Y に変換して、計算を簡単にすることができます。
Y ⇒ Δ に変換
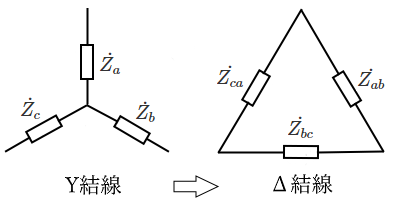
$\dot{ Z _{ab}}=\displaystyle \frac{ \dot{ Z _a}\dot{ Z _b}+ \dot{ Z _b}\dot{ Z _c}+\dot{ Z _c}\dot{ Z _a}}{ \dot{ Z _c} }$
$\dot{ Z _{bc}}=\displaystyle \frac{ \dot{ Z _a}\dot{ Z _b}+ \dot{ Z _b}\dot{ Z _c}+\dot{ Z _c}\dot{ Z _a}}{ \dot{ Z _a} }$
$\dot{ Z _{ca}}=\displaystyle \frac{ \dot{ Z _a}\dot{ Z _b}+ \dot{ Z _b}\dot{ Z _c}+\dot{ Z _c}\dot{ Z _a}}{ \dot{ Z _b} }$
尚、各相のインピーダンスが等しいときは、$\dot{ Z _Y}=\dot{ Z _a}=\dot{ Z _b}=\dot{ Z _c}$、$\dot{ Z _Δ}=\dot{ Z _{ab}}=\dot{ Z _{bc}}=\dot{ Z _{ca}}$ とすると、
$\dot{ Z _Δ}=3\dot{ Z _Y}$
平衡三相負荷の Y ⇒ Δ 変換
・負荷がインピーダンス $Z$[Ω]またはインダクタンス $L$[H]の場合
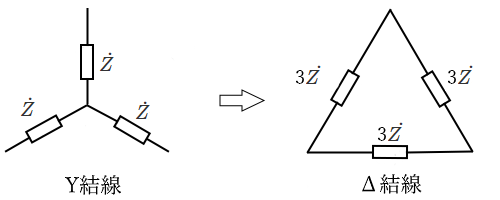
・負荷が静電容量 $C$[F]の場合
.png)
Δ ⇒ Y に変換
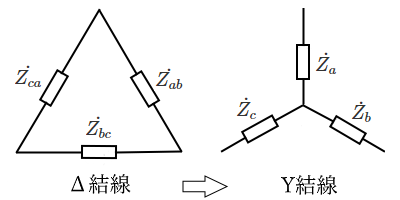
$\dot{ Z _a}=\displaystyle \frac{ \dot{ Z _{ca}}+\dot{ Z _{ab} } }{ \dot{ Z _{ab}} +\dot{ Z _{bc}}+\dot{ Z _{ca} } }$
$\dot{ Z _b}=\displaystyle \frac{ \dot{ Z _{ab}}+\dot{ Z _{bc} } }{ \dot{ Z _{ab}} +\dot{ Z _{bc}}+\dot{ Z _{ca} } }$
$\dot{ Z _c}=\displaystyle \frac{ \dot{ Z _{bc}}+\dot{ Z _{ca} } }{ \dot{ Z _{ab}} +\dot{ Z _{bc}}+\dot{ Z _{ca} } }$
尚、各相のインピーダンスが等しいときは、$\dot{ Z _Y}=\dot{ Z _a}=\dot{ Z _b}=\dot{ Z _c}$、$\dot{ Z _Δ}=\dot{ Z _{ab}}=\dot{ Z _{bc}}=\dot{ Z _{ca}}$ とすると、
$\dot{ Z _Y}=\displaystyle \frac{\dot{ Z _Δ}}{3}$
平衡三相負荷の Δ ⇒ Y 変換
・負荷がインピーダンス $Z$[Ω]またはインダクタンス $L$[H]の場合
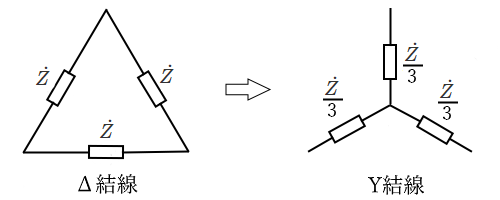
・負荷が静電容量 $C$[F]の場合
.png)
電源の Y ー Δ の相互変換
三相回路で、電源と負荷の結線方法が異なる場合には、電源側を Y ⇒ Δ または Δ ⇒ Y に変換して、計算を簡単にすることもできます。

Y結線側の相電圧が $\dot{ E _a}$,$\dot{ E _b}$,$\dot{ E _c}$ のとき、これと等価なΔ結線の相電圧 $\dot{ E _a′}$,$\dot{ E _b’}$,$\dot{ E _c’}$ は次のようになります。
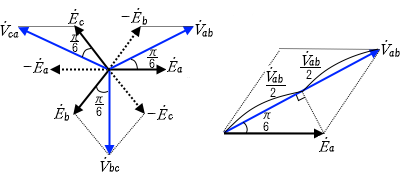
$\dot{ E _a’}=\dot{ V _{ab}}=\sqrt{3}\dot{ E _a}∠\displaystyle \frac{ π}{6}$
$\dot{ E _b’}=\dot{ V _{bc}}=\sqrt{3}\dot{ E _b}∠\displaystyle \frac{ π}{6}$
$\dot{ E _c’}=\dot{ V _{ca}}=\sqrt{3}\dot{ E _c}∠\displaystyle \frac{ π}{6}$
尚、Y結線の相電圧の大きさを $E_Y$、Δ結線の相電圧の大きさを $E_Δ$とすると、
$E_Δ=\sqrt{3}E_Y$
$E_Y=\displaystyle \frac{E_Δ}{\sqrt{3}}$
対称三相交流における電源電圧の Y ー Δ 相互変換
・Y ⇒ Δ 変換
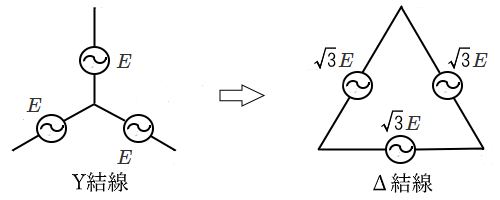
・Δ ⇒ Y 変換
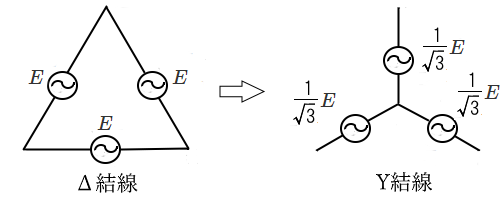
電験三種-理論の過去問解説:三相交流回路
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1998年(平成10年)問8【電験理論の過去問題】
図のような平衡三相回路において、線電流の値が 60 [A] のとき、電源の相電圧 $V$ [V] の大きさとして、正しいのは次のうちどれか。
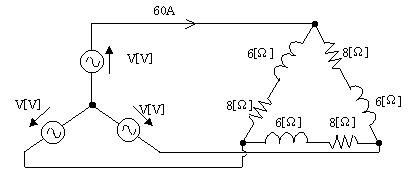
(1) 116 (2) 140 (3) 200 (4) 245 (5) 346
負荷側をΔ⇒Y変換すると、各相のインピーダンスが等しいので、インピーダンスは $\displaystyle \frac{1}{3}$になります。電源の相電圧 $V$ [V] の大きさは、
$\begin{eqnarray}V&=&IZ\\\\&=&I×\sqrt{r^2+x^2}\\\\&=&60×\sqrt{\left(\displaystyle \frac{8}{3}\right)^2+\left(\displaystyle \frac{6}{3}\right)^2}\\\\&=&200 [V] \end{eqnarray}$
答え (3)
2000年(平成12年)問6【電験理論の過去問題】
図のような平衡三相回路において、線電流 $I$ [A] の値として、正しいものは次のうちどれか。
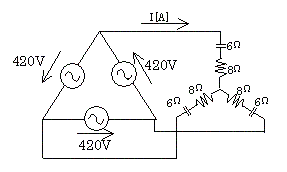
(1) 14.0 (2) 17.3 (3) 24.2 (4) 30.6 (5) 42.0
電源側をΔ⇒Y変換すると、Yに変換後の相電圧 $E_Y$ [V] は、
$E_Y=\displaystyle \frac{E_Δ}{\sqrt{3}}=\displaystyle \frac{420}{\sqrt{3}}≒242$ [V]
線電流 $I$ [A] は、
$I=\displaystyle \frac{E_Y}{Z}=\displaystyle \frac{242}{\sqrt{8^2+6^2}}=24.2$ [A]
答え (3)
2001年(平成13年)問11【電験理論の過去問題】
図のような平衡三相回路の負荷において、誘導性リアクタンス $X_L$ [Ω] に流れる電流の大きさを $I_L$ [A] 、容量性リアクタンス $X_C$ [Ω] に流れる電流の大きさを $I_C$ [A] とするとき、次の(a)及び(b)に答えよ。
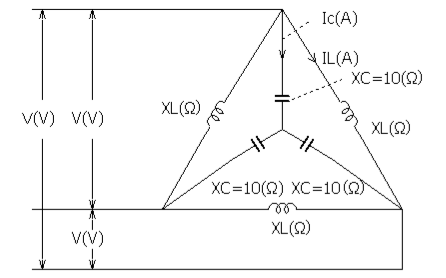
(a) $X_L$ [Ω] によるΔ結線の負荷をこれと等価なY結線の負荷に変換したとき、変換後の1相の誘導性リアクタンス $X_L’$ [Ω] に流れる電流 $I_L’$ [A] の大きさとして、正しいのは次のうちどれか。
(1) $\sqrt{3}I_L$ (2) $\sqrt{2}I_L$ (3) $I_L$ (4) $\displaystyle \frac{ 1 }{ \sqrt{2} }I_L$ (5)$\displaystyle \frac{ 1 }{ \sqrt{3} }I_L$
(b) 図の回路において、電流 $I_L$ と$I_C$ が $I_L=\displaystyle \frac{ 2 }{ \sqrt{3} }I_C$の関係にあるとき、 $X_L$ [Ω] の値として、正しいのは次のうちどれか。
(1) 5 (2) 10 (3) 15 (4) 20 (5) 25
(a) Δ結線で、誘導性リアクタンス $X_L$ [Ω] に流れる電流の大きさを $I_L$ [A] は、
$I_L=\displaystyle \frac{V}{X_L}$ [A]
誘導性リアクタンス $X_L$ [Ω] をΔ⇒Y変換したときのリアクタンスを ${X_L}’$ [Ω] とすると、各相のインピーダンスは等しいので、
${X_L}’=\displaystyle \frac{X_L}{3}$
相電圧は $E=\displaystyle \frac{V}{\sqrt{3}}$ [V] ですので、Y回路に流れる電流 ${I_L}’$ は、
${I_L}’=\displaystyle \frac{E}{\displaystyle \frac{X_L}{3}}=\displaystyle \frac{\displaystyle \frac{V}{\sqrt{3}}}{\displaystyle \frac{X_L}{3}}=\sqrt{3}\displaystyle \frac{V}{X_L}=\sqrt{3}I_L$ [V]
答え (1)
(b) $I_C=\displaystyle \frac{E}{X_C}$ ですので、題意より
$I_L=\displaystyle \frac{ 2 }{ \sqrt{3} }I_C$
$\displaystyle \frac{V}{X_L}=\displaystyle \frac{ 2 }{ \sqrt{3} }\displaystyle \frac{E}{X_C}=\displaystyle \frac{ 2 }{ 3 }\displaystyle \frac{V}{X_C}$
$X_L=\displaystyle \frac{ 3 }{ 2 }X_C=\displaystyle \frac{ 3 }{ 2 }×10=15$ [Ω]
答え (3)
2002年(平成14年)問7【電験理論の過去問題】
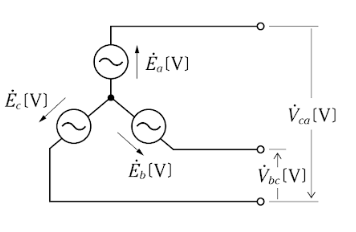
図のように、三つの交流電圧源から構成される回路において、各相の電圧 $\dot{ E_a }$ [V] ,$\dot{ E_b }$ [V] ,及び$\dot{ E_c }$ [V] は、それぞれ次のように与えられる。 ただし、式中の $∠Φ$は、$(cosΦ+jsinΦ)$ を表す。
$\dot{ E_a }=200∠0$ [V]
$\dot{ E_b }=200∠-\displaystyle \frac{ 2π }{ 3 }$ [V]
$\dot{ E_c }=200∠\displaystyle \frac{ π }{ 3 }$ [V]
このとき、図中の線間電圧 $\dot{ V }_{ca}$ [V] と $\dot{ V }_{bc}$ [V] の大きさ(スカラ量)の値として、 正しいものを組み合わせたのは次のうちどれか。
| 線間電圧 $\dot{ V }_{ca}$ [V] の電圧 | 線間電圧 $\dot{ V }_{bc}$ [V] の電圧 | |
| (1) | $200$ | $0$ |
| (2) | $200\sqrt{3}$ | $200\sqrt{3}$ |
| (3) | $200\sqrt{3}$ | $400\sqrt{3}$ |
| (4) | $200\sqrt{3}$ | $400$ |
| (5) | $200$ | $400$ |
問をベクトル図で示します。
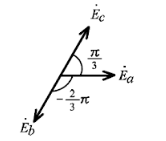
図より、線間電圧 $\dot{ V }_{ca}$ の電圧は 200 [V] 、線間電圧 $\dot{ V }_{bc}$ の電圧は 400 [V]
答え (5)
2003年(平成15年)問7【電験理論の過去問題】
図の対称三相交流電源の各相の電圧は、それぞれ $\dot{ E _a}=200∠0$ [V] ,$\dot{ E _b}=200∠-\displaystyle \frac{ 2π }{ 3 }$ [V] 及び $\dot{ E_c }=200∠-\displaystyle \frac{ 4π }{ 3 }$ [V] である。この電源には、抵抗 40 [Ω] をΔ結線した三相平衡負荷が接続されている。このとき、線間電圧 $\dot{ V }_{ab}$ [V] と線電流 $\dot{ I_a}$ [A] の大きさ(スカラ量)の値として、最も近いものを組み合わせたのは次のうちどれか。
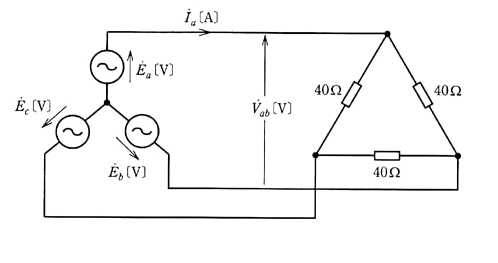
| 線間電圧 $\dot{ V }_{ab}$ [V] の大きさ | 線電流 $\dot{ I_a}$ [A] の大きさ | |
| (1) | 283 | 5 |
| (2) | 283 | 8.7 |
| (3) | 346 | 8.7 |
| (4) | 346 | 15 |
| (5) | 400 | 15 |
線間電圧 $\dot{ V_{ab} }$ [V] の大きさは、相電圧 $\dot{ E _a}$ [V] の $\sqrt{3}$ 倍ですので、
$ V_{ab}=\sqrt{3} E _a=\sqrt{3}×200=346$ [V]
相電流を $I_p$ [A] とすると、
$I_p=\displaystyle{ V_{ab}}{R}=\displaystyle{ 346}{40}=8.65$ [A]
線電流 $I_a$ [A] と、相電流を $I_p$ [A] は、$I_a=\sqrt{3}I_p$ [A] の関係がありますので、
$I_a=\sqrt{3}I_p=\sqrt{3}×8.65=15$ [A]
答え (4)
2009年(平成21年)問16【電験理論の過去問題】
平衡三相回路について、次の(a)及び(b)に答えよ。
(a) 図1のように、抵抗 $R$ [Ω] が接続された平衡三相負荷に線間電圧 $E$ [V] の対称三相交流電源を接続した。この時、図1に示す電流 $\dot{ I_1}$ [A] の大きさの値を示す式として、正しいのは次のうちどれか。
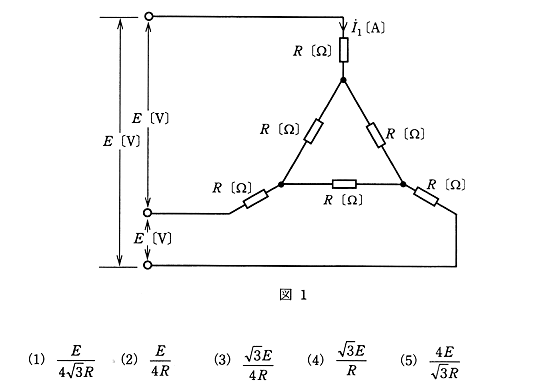
(b) 次に、図1を図2のように、抵抗 $R$ [Ω] をインピーダンス $\dot{ Z}=12+j9$ [Ω] の負荷に置き換え、線間電圧 $E=200$ [V] とした。このとき、図2に示す電流 $\dot{ I_2}$ [A] の大きさの値として、最も近いのは次のうちどれか。
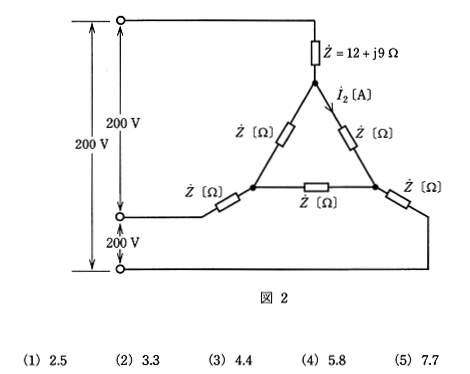
(a) 抵抗負荷の中央部分をΔ⇒Y変換すると、抵抗値は $\displaystyle \frac{R}{3}$ になります。一相分の抵抗は、$R+\displaystyle \frac{R}{3}$ ですので、電流 $\dot{ I_1}$ [A] は、
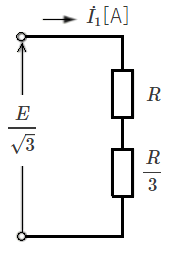
$\dot{ I_1}=\displaystyle \frac{\displaystyle \frac{E}{\sqrt{3}}}{R+\displaystyle \frac{R}{3}}=\displaystyle \frac{\sqrt{3}E}{4R}$ [A]
答え (3)
(b) 中央部分をΔ⇒Y変換すると、次の図のようになります。 電流 $\dot{ {I_2}’}$ [A] は、
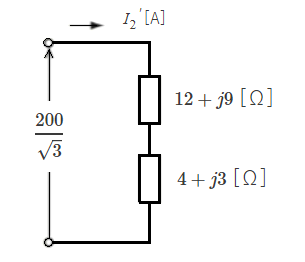
$\dot{ {I_2}’}=\displaystyle \frac{\displaystyle \frac{200}{\sqrt{3}}}{(12+j9)+(4+j3)}=\displaystyle \frac{200}{\sqrt{3}(16+j12)}$
$\dot{ {I_2}’}$ の大きさは
$ {I_2}’=\displaystyle \frac{200}{\sqrt{3}×\sqrt{16^2+12^2}}=5.77$ [A]
${I_2}’$ は線電流ですので、相電流の大きさ $I_2$ は、
$I_2=\displaystyle \frac{5.77}{\sqrt{3}}=3.3$ [A]
答え (2)
2012年(平成24年)問16【電験理論の過去問題】
図のように、相電圧 200 [V] の対称三相交流電源に、複素インピーダンス $\dot{ Z}=5\sqrt{3}+j5$ [Ω] の負荷がY結線された平衡三相負荷を接続した回路がある。
次の(a)及び(b)の問に答えよ。
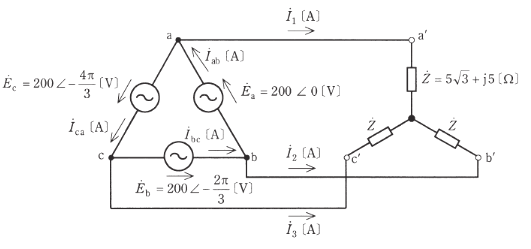
(a) 電流 $I_1$ [A] の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) $20.00∠-\displaystyle \frac{ π }{ 3 }$ (2) $20.00∠-\displaystyle \frac{ π }{ 6 }$ (3) $16.51∠-\displaystyle \frac{ π }{ 6 }$ (4) $11.55∠-\displaystyle \frac{ π }{ 3 }$ (5) $11.55∠-\displaystyle \frac{ π }{ 6 }$
(b) 電流 $I_{ab}$ [A] の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) $20.00∠-\displaystyle \frac{ π }{ 6 }$ (2) $11.55∠-\displaystyle \frac{ π }{ 3 }$ (3) $11.55∠-\displaystyle \frac{ π }{ 6 }$ (4) $6.67∠-\displaystyle \frac{ π }{ 3 }$ (5) $6.67∠-\displaystyle \frac{ π }{ 6 }$
(a) 電源側をΔ⇒Y変換し、Δ側の相電圧 $\dot{ E _a}$ を基準にしたベクトル図を示します。
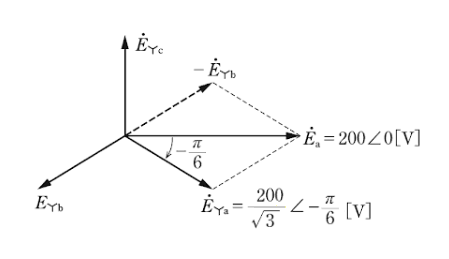
図より、Δ結線をY結線に変換すると、相電圧は線間電圧の $\displaystyle \frac{1}{\sqrt{3}}$ になり、位相は $\displaystyle \frac{π}{6}$ 遅れます。
$\dot{ E _{Ya}}=\displaystyle \frac{\dot{ E _a}}{\sqrt{3}}∠-\displaystyle \frac{π}{6}=\displaystyle \frac{200}{\sqrt{3}}∠(0-\displaystyle \frac{π}{6})=\displaystyle \frac{200}{\sqrt{3}}∠-\displaystyle \frac{π}{6}$
一相分の負荷のインピーダンス $\dot{Z}$ [Ω] は、大きさが 10 [Ω] で、インピーダンス角が $\displaystyle \frac{π}{6}$ ですので、
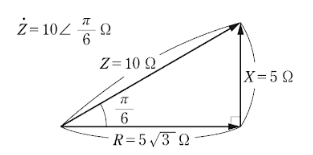
$\dot{Z}=10∠\displaystyle \frac{π}{6}$ [Ω]
したがって、電流 $I_1$ [A] は、
$I_1=\displaystyle \frac{\dot{ E _{Ya}}}{\dot{Z}}=\displaystyle \frac{\displaystyle \frac{200}{\sqrt{3}}∠-\displaystyle \frac{π}{6}}{10∠\displaystyle \frac{π}{6}}=11.55∠-\displaystyle \frac{π}{3}$ [A]
答え (4)
(b) a相の電流をの関係をベクトル図を示します。
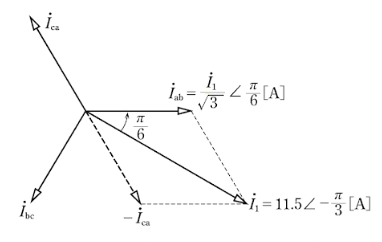
図より、相電流は線電流の $\displaystyle \frac{1}{\sqrt{3}}$ になり、位相は $\displaystyle \frac{π}{6}$ 進みます。
$\dot{I_{ab}}=\displaystyle \frac{\dot{I_{1}}}{\sqrt{3}}∠\displaystyle \frac{π}{6}=\displaystyle \frac{11.55}{\sqrt{3}}∠-\displaystyle \frac{π}{3}+\displaystyle \frac{π}{6}=6.67∠-\displaystyle \frac{π}{6}$ [A]
答え (5)
2016年(平成28年)問15【電験理論の過去問題】
図のように、$r$ [Ω] の抵抗6個が線間電圧の大きさ $V$ [V] の対称三相電源に接続されている。b相の×印の位置で断線し、c-a相間が単相状態になったとき、次の(a)及び(b)の問に答えよ。
ただし、電源の線間電圧の大きさ及び位相は、断線によって変化しないものとする。
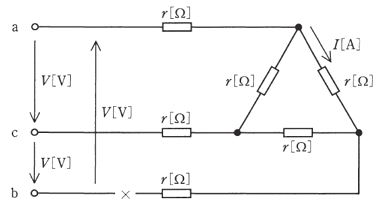
(a) 図中の電流 $I$ の大きさ [A] は、断線前の何倍となるか。その倍率として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.50 (2) 0.58 (3) 0.87 (4) 1.15 (5) 1.73
(b) ×印の両側に現れる電圧の大きさ [V] は、電源の線間電圧の大きさ $V$ [V] の何倍となるか。その倍率として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0 (2) 0.58 (3) 0.87 (4) 1.00 (5) 1.15
(a) 断線前の負荷側をΔ⇒Y変換した一相分の等価回路は、次の図のようになります。断線前では、相電流の大きさ $I_p$[A]は、
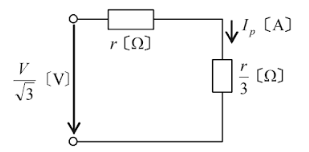
$I_p=\displaystyle \frac{\displaystyle \frac{V}{\sqrt{3}}}{r+\displaystyle \frac{r}{3}}=\displaystyle \frac{\sqrt{3}V}{4r}$ [A]
Δ結線の電流 $I$ [A] は、
$I=\displaystyle \frac{I_p}{\sqrt{3}}=\displaystyle \frac{V}{4r}$ [A]
b相の×印の位置で断線した時の等価回路を示します。流れる電流の大きさを $I’$ [A] とすると、
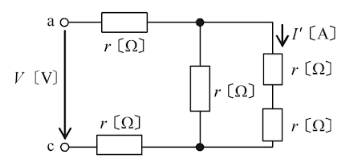
$I’=\displaystyle \frac{V}{2r+\displaystyle \frac{r×2r}{r+2r}}×\displaystyle \frac{r}{r+2r}=\displaystyle \frac{V}{8r}$
したがって、断線前の倍率は、
$\displaystyle \frac{I’}{I}=\displaystyle \frac{\displaystyle \frac{V}{8r}}{\displaystyle \frac{V}{4r}}=0.5$
答え (1)
(b) 電圧のベクトル図を示します。
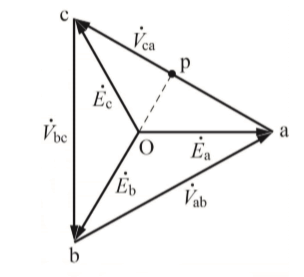
断線後、断線部の両側の電圧は、点aと点cの中点Pの電位と、点bの電位差になります。線間電圧の大きさを $V$ とすると、点Pの電位と、点bの電位差 OP は $\displaystyle \frac{\sqrt{3}}{2}V$ ですので、その倍率は、
$\displaystyle \frac{\displaystyle \frac{\sqrt{3}}{2}V}{V}=0.87$
答え (3)
電験三種の理論科目に出題される「単相交流分野」のページ
1.正弦波交流の波形
2.単相交流の直列回路
3.単相交流の並列回路
4.RLC直列共振回路
5.RLC並列共振回路
6.単相交流の電力と力率
電験三種の理論科目に出題される「三相交流分野」のページ
1.三相交流回路
2.三相交流の電力と力率




