このページでは、分岐回路とループ回路の送電電力について、初心者の方でも解りやすいように、基礎から解説しています。また、電験三種の電力科目の試験で、実際に出題された分岐回路とループ回路の過去問題も解説しています。
- 分岐回路の電圧降下
- ループ回路の電圧降下
- 電験三種-電力(送配電)過去問題
- 2000年(平成12年)問12
- 2000年(平成12年)問12 過去問解説
- 2001年(平成13年)問12
- 2001年(平成13年)問12 過去問解説
- 2003年(平成15年)問17
- 2003年(平成15年)問17 過去問解説
- 2004年(平成16年)問14
- 2004年(平成16年)問14 過去問解説
- 2005年(平成17年)問17
- 2005年(平成17年)問17 過去問解説
- 2010年(平成22年)問17
- 2010年(平成22年)問17 過去問解説
- 2013年(平成25年)問13
- 2013年(平成25年)問13 過去問解説
- 2015年(平成27年)問16
- 2015年(平成27年)問16 過去問解説
- 2016年(平成28年)問13
- 2016年(平成28年)問13 過去問解説
分岐回路の電圧降下
図のような三相3線式配電線路で、電源側S点の線間電圧が 6600[V]のとき、A点及びB点の線間電圧[V]の値を求めてみます。ただし、Z1,Z2 は、電線1線当たりのインピーダンスを示します。
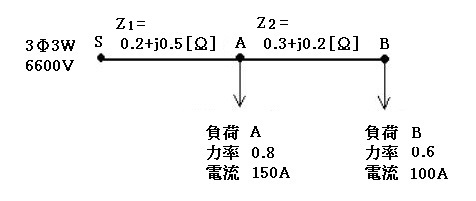
A-B間の電圧降下を求めます。A-B間は、B点の負荷電流のみが流れますので、電圧降下を VLAB とすると、
$\begin{eqnarray}V_{LAB}&=&\displaystyle \sqrt{ 3 }I_B(r_2cosθ_B+x_2sinθ_B)\\&=&\displaystyle \sqrt{ 3 }×100×(0.3×0.6+0.2×0.8)\\&=&58.9[V]\end{eqnarray}$
0.2+5j[Ω]は r が 0.2[Ω]、x が 0.5[Ω]です。
S-A間の電圧降下を求めます。S-A間は、A点とB点の負荷電流が流れますので、両方の負荷による電圧降下を合算します。S-A間の電圧降下を VLSA とすると、
$\begin{eqnarray}V_{LSA}&=&\displaystyle \sqrt{ 3 }I_A(r_1cosθ_A+x_1sinθ_A)+\displaystyle \sqrt{ 3 }I_B(r_1cosθ_B+x_1sinθ_B)\\&=&\displaystyle \sqrt{ 3 }×150×(0.2×0.8+0.5×0.6)+\displaystyle \sqrt{ 3 }×100×(0.2×0.6+0.5×0.8)\\&=&209.6[V]\end{eqnarray}$
A点、B点の線間電圧を求めます。
A点の線間電圧
$V_A=6600-209.6=6390.4$[V]
B点の線間電圧
$V_B=V_A-58.9=6331.5$[V]
ループ回路の電圧降下
図のような単相2線式線路で、電源側F点の線間電圧が 100[V]で負荷の力率が 100[%]のとき、A点及びB点の線間電圧[V]の値を求めてみます。ただし、r1,r2,r3 は、往復線の抵抗値を示します。
二通りの解きかたを示します。
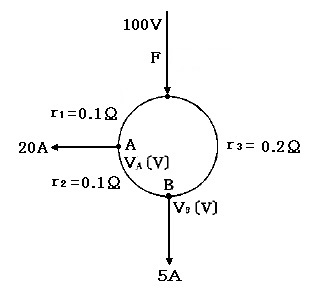
左回りと右回りで、電圧降下が一致と考えて解く
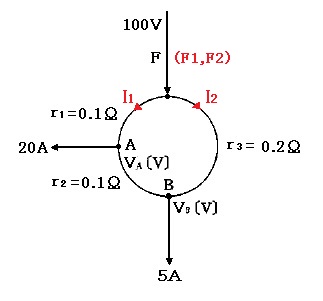
回路中の1点の電流に注目し、左回りと右回りの電圧降下が等しくなると考えて、電流・電圧の分布を考えます。例題では、B点について注目をしてみます。左回りの電流を I1、右回りの電流を I2 とします。
左回り、「F1→A→B」間の電圧降下を EF1 とすると、
$E_{F1}=0.1I_1+0.1(I_1-20)$
左回り、「F1→B」間の電圧降下を EF2 とすると、
$E_{F2}=0.2I_2$
左回りと右回りの電圧降下が等しくなると考えますので、
$0.1I_1+0.1(I_1-20)=0.2I_2$
$I_1-10=I_2 … (1)$
B点の電流は 5A ですので、回路より
$I_1-20+I_2=5 … (2)$
(1)、(2)を解くと、
$I_1=17.5$、$I_2=7.5$[A]
電流の分布は次の図のようになります。
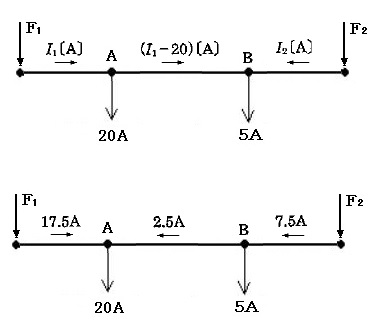
AB間の電流はB→Aに 2.5[A]流れることになります。よって、A点、B点の線間電圧は、F点からA点、B点までの電圧降下分を引きます。
A点の線間電圧
$V_A=100-17.5×0.1=98.25$[V]
B点の線間電圧
$V_B=100-7.5×0.2=98.5$[V]
ループ全体の電圧降下が0と考えて解く
キルヒホッフの法則を用いてループ回路全体の電圧降下が 0 になると考え、電圧・電流分布を考えます。
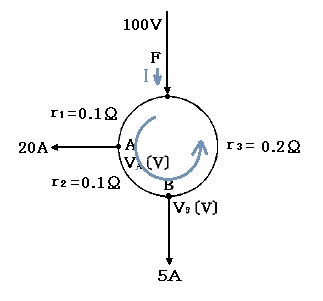
図のように「F→A→B→F」と電流が一巡するようにたどって、電圧降下を考えます。
$0.1I+0.1(I-20)+0.2(I-20-5)=0$
$I=17.5$[A]
となりますので、上の例と同じように、各点の電圧降下を考えて計算すれば、求めることができます。
電験三種-電力(送配電)過去問題
2000年(平成12年)問12
図の単線結線図に示す単相2線式の回路がある。供給点Kにおける線間電圧 VK は 105[V]、負荷点L,M,Nには、それぞれ電流値が 40[A],50[A],10[A]で、ともに力率 100[%]の負荷が接続されている。
回路の1線当たりの抵抗はKL間が 0.1[Ω],LN間が 0.05[Ω],KM間が 0.05[Ω],MN間が 0.1[Ω]であり、線路のリアクタンスは無視するものとして、次の(a)及び(b)に答えよ。
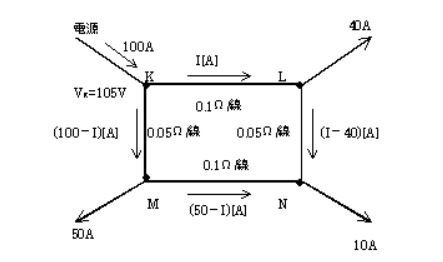
(a) 供給点Kと負荷点L間に流れる電流 I[A]の値として、正しいのは次のうちどれか。
(1) 30 (2) 40 (3) 50 (4) 60 (5) 100
(b) 負荷点Nの電圧[V]の値として、正しいのは次のうちどれか。
(1) 97 (2) 98 (3) 99 (4) 100 (5) 101
2000年(平成12年)問12 過去問解説
(a) ループ回路全体の電圧降下は 0 になりますので、キルヒホッフの法則を適用します。
0.2I+0.1(I-40)-0.2(50-I)-0.1(100-I)=0
I=40[A]
(2線式ですので、おのおのの抵抗値は2倍になります。)
答え (2)
(b) N点の電圧は、K点から、N点までの電圧降下を引きます。
VN=105-2(0.1×40)-2(0.05×(40-40))=97[V]
(2線式ですので、電圧降下は2倍になります。)
答え (1)
2001年(平成13年)問12
図のような、A点及びB点に負荷を有する三相3線式高圧配電線がある。電源側S点の線間電圧を 6600[V]とするとき、次の(a)及び(b)に答えよ。
ただし、配電線1線当たりの抵抗及びリアクタンスはそれぞれ 0.3[Ω/km]とする。
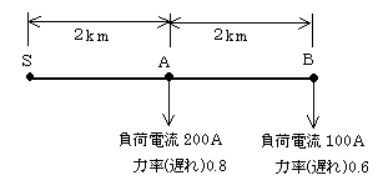
(a) S-A間に流れる有効電流[A]の値として、正しいのは次のうちどれか。
(1) 140 (2) 160 (3) 200 (4) 220 (5) 240
(b) B点における線間電圧[V]の値として、最も近いのは次のうちどれか。
(1) 5770 (2) 6020 (3) 6130 (4) 6260 (5) 6460
2001年(平成13年)問12 過去問解説
(a) S-A間に流れる電流 I は、A点から分岐した負荷電流とB点から分岐した負荷電流の和になります。分岐した負荷電流のベクトル図を示します。
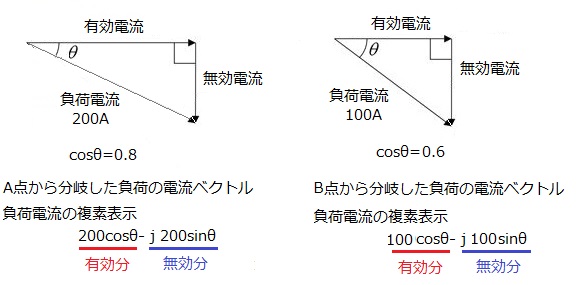
$\begin{eqnarray}I&=&200(cosθ-jsinθ)+100(cosθ-jsinθ)\\&=&200(0.8-j0.6)+100(0.6-j0.8)\\&=&220-j200\end{eqnarray}$
S-A間に流れる有効電流は 220[A]、無効電流は 200[A]になります。
答え (4)
(b) A-B間の電圧降下を求めます。A-B間は、B点の負荷電流のみが流れますので、電圧降下を VLAB とすると、
$\begin{eqnarray}V_{LAB}&=&\sqrt{ 3 }I(rcosθ+xsinθ)\\&=&\sqrt{ 3 }×100×(0.3×2×0.6+0.3×2×0.8)\\&=&145.5[V]\end{eqnarray}$
S-A間の電圧降下を求めます。S-A間は、A点とB点の負荷電流が流れますので、両方の電圧降下を合算します。S-A間の電圧降下を VLSA とすると、
$\begin{eqnarray}V_{LSA}&=&\sqrt{ 3 }×200×(0.3×2×0.8+0.3×2×0.6)\\&+&\sqrt{ 3 }×100×(0.3×2×0.6+0.3×2×0.8)\\&=&436.5[V]\end{eqnarray}$
B点における線間電圧[V]は、
$V_B=6600-436.5-145.5=6018$[V]
答え (2)
2003年(平成15年)問17
図のような単相2線式配電線路で、K,L,M,Nの 4地点の負荷に電力を供給している。電線の種類、太さは全区間同一で、電線の抵抗は 1[km]当たり 0.48[Ω]、負荷の力率はいずれも 100[%]として、次の(a)及び(b)に答よ。
ただし、線路リアクタンスは無視するものとする。
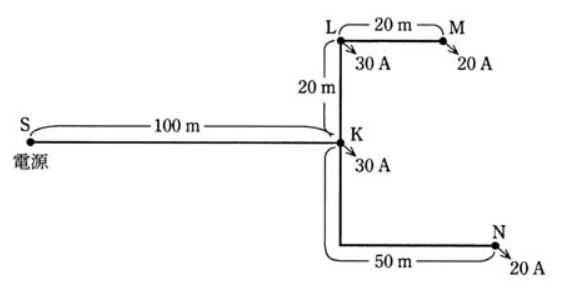
(a) 電源S点からの電圧降下が最も大きい地点での電圧降下[V]の値として、最も近いのは次のうちどれか。
(1) 2.7 (2) 9.6 (3) 10.5 (4) 10.9 (5) 21.5
(b) L地点の負荷が増加して 50[A]になったとき、電圧降下の最も大きい地点での電圧降下が、前の値より大きくならないようにSK間の電線を張り替えることとした。SK間の新しい電線の 1[km]当たりの抵抗[Ω]の最大値として、最も近いのは次のうちどれか。
(1) 0.28 (2) 0.34 (3) 0.38 (4) 0.42 (5) 0.46
2003年(平成15年)問17 過去問解説
(a) 電流と抵抗値の分布図を示します。
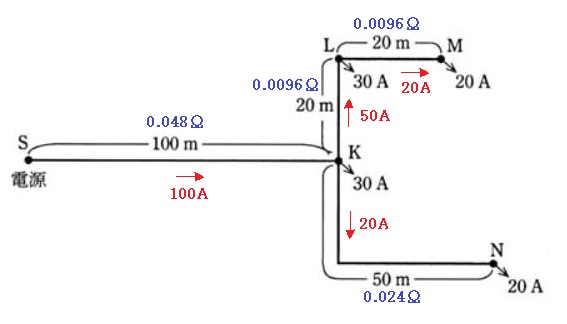
末端に行くほど、電圧降下は大きくなりますので、N点とM点の電圧降下を比較します。
$\begin{eqnarray}V_{M}&=&2×0.048×100+2×0.0096×50+2×0.0096×20\\&=&10.944[V]\end{eqnarray}$
$\begin{eqnarray}V_{N}&=&2×0.048×100+2×0.024×20\\&=&10.56[V]\end{eqnarray}$
$V_{M}>V_{N}$
答え (4)
(b) 増加した電流の分布図を示します。尚、抵抗値は元のまま考えます。
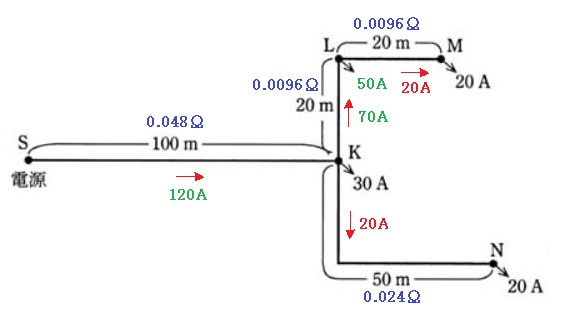
S-K-L間で、電流を20A分電流が増加したため、電圧降下も増加します。電圧降下増加分を ΔV とすると、
$ΔV=2×(0.048+0.0096)×20=2.304$[V]
この電圧降下増加分 $ΔV$ のSK間の電線の抵抗値 $ΔR$ は、
$ΔR=\displaystyle \frac{ 2.304}{ 2×120 }=0.0096$[Ω]
このSK間の電線の抵抗値 ΔR を減らすことで、電圧降下が前の値より大きくなりません。つまりSK間の抵抗値が、
$0.048-0.0096=0.0384$[Ω]
になります。求める解は、 1[km]当たりの抵抗[Ω]の最大値ですので、
$0.0384×\displaystyle \frac{ 1000}{ 100 }=0.38$[Ω/km]
答え (3)
2004年(平成16年)問14
図のような三相3線式配電線路で、各負荷に電力を供給する場合、全線路の電圧降下[V]の値として、最も近いのは次のうちどれか。
ただし、電線の太さは全区間同一で抵抗は 1[km]当たり 0.35[Ω]、負荷の力率はいずれも 100[%]で線路のリアクタンスは無視するものとする。
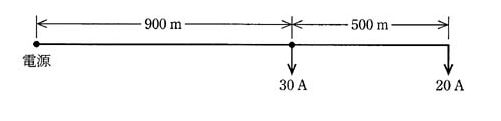
(1) 19.3 (2) 22.4 (3) 33.3 (4) 38.5 (5) 57.8
2004年(平成16年)問14 過去問解説
負荷の力率は力率 100% なので、電流と抵抗値の分布は図のようになります。
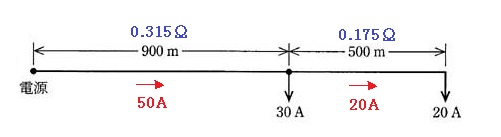
電圧降下は $V_L=\sqrt{ 3 }I(rcosθ+xsinθ)$ で求められます。題意より負荷の力率は 100[%]で線路のリアクタンスは無視しますので、全線路の電圧降下は
$V_L=\sqrt{ 3 }×50×0.315+ \sqrt{ 3 }×20×0.175=33.3$[V]
答え (3)
2005年(平成17年)問17
図の単線結線図に示す単相2線式1回線の配電線路がある。供給点Aにおける線間電圧 VA は 105[V]、負荷点K,L,M,Nにはそれぞれ電流値が 30[A],10[A],40[A],20[A]でともに力率 100[%]の負荷が接続されている。回線1線当たりの抵抗はAK間が 0.05[Ω],KL間が 0.04[Ω],LM間が 0.07[Ω],MN間が 0.05[Ω]、NA間が 0.04[Ω]であり、線路のリアクタンスは無視するものとして、次の(a)及び(b)に答えよ。
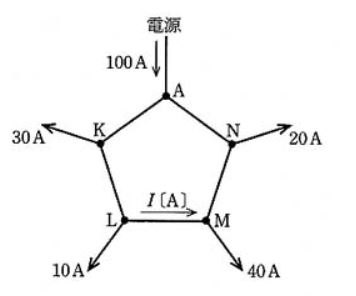
(a) 負荷点Lと負荷点M間に流れる電流 I[A]の値として、正しいのは次のうちどれか。
(1) 4 (2) 6 (3) 8 (4) 10 (5) 12
(b) 負荷点Mの電圧[V]の値として、最も近いのは次のうちどれか。
(1) 95.8 (2) 97.6 (3) 99.5 (4) 101.3 (5) 103.2
2005年(平成17年)問17 過去問解説
(a) 電流と抵抗値の分布図を示します。ループ回路全体の電圧降下は 0 になりますので、キルヒホッフの法則を適用します。
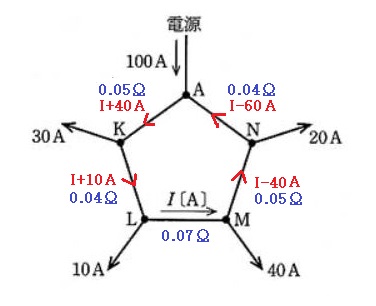
$0.05(I+40)+0.04(I+10)+0.07I+0.05(I-40)+0.04(I-60)=0$
$I=8$[A]
答え (3)
(b) M点の電圧は、A点からM点までの電圧降下を引きます。区間A→N→Mで考えると
$105-2×0.04×\{-(8-60)\}-2×0.05×\{-(8-40)\}=97.64$[V]
(2線式ですので、電圧降下は2倍になります。電流の向きに注意が必要です。)
答え (2)
2010年(平成22年)問17
図は単相2線式の配電線路の単線図である。電線1線当たりの抵抗と長さは、a-b間で 0.3 [Ω/km],250[m]、b-c間で 0.9[Ω/km],100[m]とする。次の(a)及び(b)に答えよ。
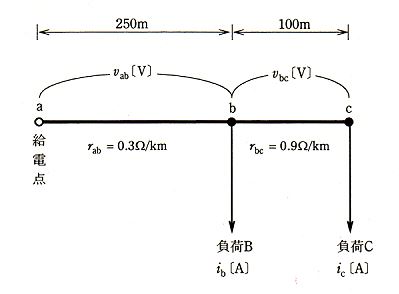
(a) b-c間の1線の電圧降下 Vbc[V]及び負荷Bと負荷Cの負荷電流 ib、 ic[A]として、正しいものを組み合わせたのは次のうちどれか。
ただし、給電点aの線間の電圧値と負荷点cの線間の電圧値の差を 12.0[V]とし、a-b間の1線の電圧降下 Vab= 3.75[V]とする。負荷の力率はいずれも 100[%]、線路リアクタンスは無視するものとする。
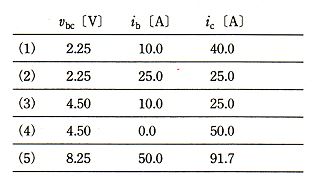
(b) 次に、図の配電線路で抵抗に加えてa-c間の往復線路のリアクタンスを考慮する。このリアクタンスを 0.1[Ω]とし、b点には無負荷で ib=0[A]、c点には受電電圧が 100[V]、遅れ力率 0.8,1.5[kW]の負荷が接続されているものとする。
このとき、給電点aの線間の電圧値と負荷点cの線間の電圧値[V]の差として、最も近いのは次のうちどれか。
(1) 3.0 (2) 4.9 (3) 5.3 (4) 6.1 (5) 37.1
2010年(平成22年)問17 過去問解説
(a) Vab=3.75[V]ですので、a-b間に流れる電流 i[A]は、
$i=\displaystyle \frac{ V_{ab}}{ r_{ab}×0.25 }=\displaystyle \frac{ 3.75}{ 0.3×0.25 }=50$[A]
給電点aの線間の電圧値と負荷点cの線間の電圧値の差は 12.0[V]ですので、a-c間の1線の電圧降下 Vac[V]は
$V_{ac}=\displaystyle \frac{ 12.0}{ 2 }=6.0$[V]
b-c間の1線の電圧降下 Vbc[V]は、
$V_{bc}=Vac-Vab=6.0-3.75=2.25$[V]
b-c間に流れる電流 ic[A]は、
$i_c=\displaystyle \frac{ V_{bc}}{ r_{bc}×0.1 }=\displaystyle \frac{ 2.25}{ 09×0.1 09}=25$[A]
i=ib+ic なので、
$i_b=50-25=25$ [A]
答え (2)
(b) 問題文を図に示します。
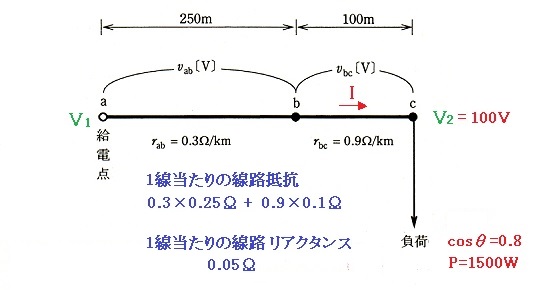
$P=V_2Icosθ$より、
$I=\displaystyle \frac{ P}{ V_2cosθ }=\displaystyle \frac{ 1500}{ 100×0.8 }=18.75$[A]
電圧降下 $V_L$は、次の式で求めることができます。
$V_L=V_1-V_2=2I(rcosθ+xsinθ)$
つまり、電圧降下が給電点aの線間の電圧値と負荷点cの線間の電圧値[V]の差になります。
$2I(rcosθ+xsinθ)=2×18.75×((0.3×0.25+0.9×0.1)×0.8+0.05×0.6)=6.1$[V]
答え (4)
2013年(平成25年)問13
図のような三相 3 線式配電線路において、電源側S点の線間電圧が 6900[V]のとき、B点の線間電圧[V]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、配電線 1 線当たりの抵抗は 0.3 [Ω/km]、リアクタンスは 0.2 [Ω/km] とする。
また、計算においては S点、 A点及びB点における電圧の位相差が十分小さいとの仮定に基づき適切な近似を用いる。
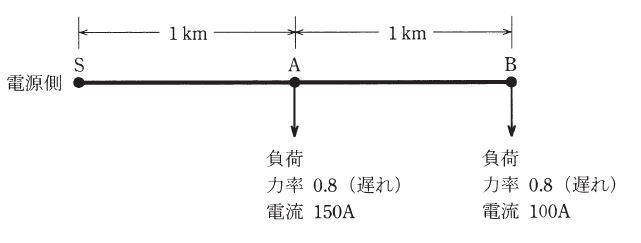
(1) 6522 (2) 6646 (3) 6682 (4) 6774 (5) 6795
2013年(平成25年)問13 過去問解説
A-B間の電圧降下を求めます。A-B間は、B点の負荷電流のみが流れますので、電圧降下を VLAB とすると、
$\begin{eqnarray}V_{LAB}&=&\sqrt{ 3 }I_B(r_2cosθ_B+x_2sinθ_B)\\&=&\sqrt{ 3 }×100×(0.3×0.8+0.2×0.6)\\&=&62.4[V]\end{eqnarray}$
S-A間の電圧降下を求めます。S-A間は、A点とB点の負荷電流が流れますので、両方の負荷による電圧降下を合算します。S-A間の電圧降下を VLSA とすると、
$\begin{eqnarray}V_{LSA}&=&\sqrt{ 3 }I_A(r_1cosθ_A+x_1sinθ_A)\\&+&\sqrt{ 3 }I_B(r_1cosθ_B+x_1sinθ_B)\\\\&=&\sqrt{ 3 }×150×(0.3×0.8+0.2×0.6)\\&+&\sqrt{ 3 }×100×(0.3×0.8+0.2×0.6)\\\\&=&155.9[V]\end{eqnarray}$
$\begin{eqnarray}V_{LSA}&=&\sqrt{ 3 }I_A(r_1cosθ_A+x_1sinθ_A)\\&+&\sqrt{ 3 }I_B(r_1cosθ_B+x_1sinθ_B)\\\\&=&\sqrt{ 3 }×150×(0.3×0.8+0.2×0.6)\\&+&\sqrt{ 3 }×100×(0.3×0.8+0.2×0.6)\\\\&=&155.9[V]\end{eqnarray}$
B点の線間電圧 VB を求めます。
$V_B=6900-155.9-62.4=6681.7$[V]
答え (3)
2015年(平成27年)問16
図は、三相3線式変電設備を単線図で表したものである。
現在、この変電設備は、a点から 3800kV・A、遅れ力率 0.9の負荷Aと、b点から 2000kW、遅れ力率 0.85の負荷Bに電力を供給している。b点の線間電圧の測定値が 22000V であるとき、次の(a)及び(b)の問に答えよ。
なお、f点とa点の間は 400m、a点とb点の間は 800mで、電線1条当たりの抵抗とリアクタンスは 1km当たり 0.24Ωと 0.18Ωとする。また、負荷は平衡三相負荷とする。
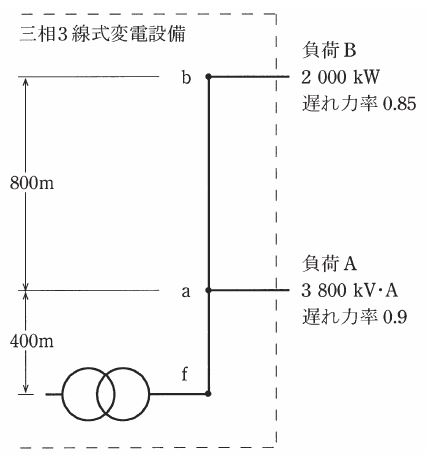
(a) 負荷Aと負荷Bで消費される無効電力の合計値[kvar]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 710 (2) 2900 (3) 3080 (4) 4880 (5) 5120
(b) f-b間の線間電圧の電圧降下 Vfbの値 [V]として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、送電端電圧と受電端電圧との相差角が小さいとして得られる近似式を用いて解答すること。
(1) 23 (2) 33 (3) 59 (4) 81 (5) 101
2015年(平成27年)問16 過去問解説
(a) 問題文は、負荷Aは皮相電力、負荷Bは有効電力で表されています。負荷Bの皮相電力を SB[kV・A]とすると、
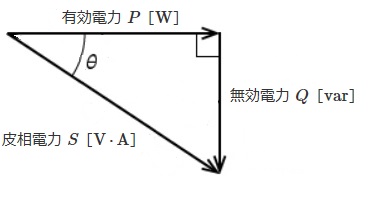
$S_B=\displaystyle \frac{ 2000}{0.85 }$[kV・A]
負荷Aと負荷Bの無効電力をそれぞれ QA、QB[kvar]とすると、
$Q_A=3800×\sqrt{ 1-0.9^2 }=1656$[kvar]
$Q_B=\displaystyle \frac{ 2000}{0.85 }×\sqrt{ 1-0.85^2 }=1239$[kvar]
無効電力の合計値は、
$Q_A+Q_B=2895$[kvar]
答え (2)
(b) 問題文を図に示します。
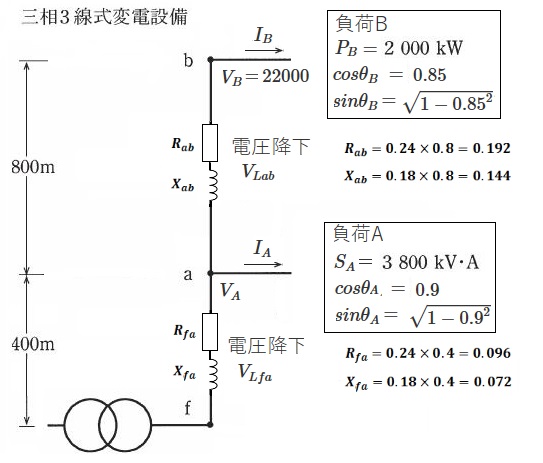
負荷Bに流れる電流 IB は、
$P_B=\sqrt{ 3 }V_BI_Bcosθ_B$
$2000×10^3=\sqrt{ 3 }×22000×I_B×0.85$
$I_B=61.75$
a-b間の電圧降下を求めます。a-b間は、Bの負荷電流のみが流れますので、電圧降下を VLab とすると、
$\begin{eqnarray}V_{Lab}&=&\sqrt{ 3 }I_B(R_{ab}cosθ_B+X_{ab}sinθ_B)\\&=&\sqrt{ 3 }×61.75×(0.192×0.85+0.114×\sqrt{ 1-0.85^2 })\\&=&25.57[V]\end{eqnarray}$
a点の電圧 VA は
$V_A=V_B+V_{Lab}=22000+25.57=22025.57$[V]
になりますので、負荷Aに流れる電流 IA は、
$S_A=\sqrt{ 3 }V_AI_A$
$3800×10^3=\sqrt{ 3 }×22025.57×I_A$
$I_A=99.61$
f-a間の電圧降下を求めます。f-a間は、AとBの負荷電流が流れますので、両方の負荷による電圧降下を合算します。f-a間の電圧降下を VLfa とすると、
$\begin{eqnarray}V_{Lfa}&=&\sqrt{ 3 }I_A(R_{fa}cosθ_A+X_{fa}sinθ_A)\\&+&\sqrt{ 3 }I_B(R_{fa}cosθ_B+X_{fa}sinθ_B)\\\\&=&\sqrt{ 3 }×99.61×(0.096×0.9+0.072×\sqrt{ 1-0.9^2 })\\&+&\sqrt{ 3 }×61.75×(0.096×0.85+0.072×\sqrt{ 1-0.85^2 })\\\\&=&33.10[V]\end{eqnarray}$
電圧降下の合計は、
$V_{Lab}+V_{Lfa}=25.57+33.10=58.67$[V]
答え (3)
2016年(平成28年)問13
図のような単相2線式線路がある。母線F点の線間電圧が 107Vのとき、B点の線間電圧が 96Vになった。B点の負荷電流 I[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、使用する電線は全て同じものを用い、電線1条当たりの抵抗は、1km当たり 0.6Ωとし、抵抗以外は無視できるものとする。また、全ての負荷の力率は 100%とする。
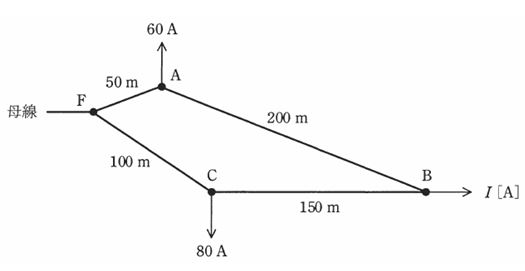
(1) 29.3 (2) 54.3 (3) 84.7 (4) 102.7 (5) 121.3
2016年(平成28年)問13 過去問解説
電流と抵抗値の分布図を示します。
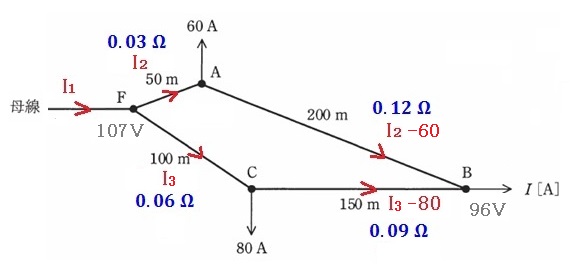
「F→A→B」間の電圧降下を考えます。
$107-0.06I_2-0.24(I_2-60)=96$
$I_2=84.67$[A]
「F→C→B」間の電圧降下を考えます。
$107-0.12I_3-0.18(I_3-80)=96$
$107-0.12I_3-0.18(I_3-80)=96$ $I_3=84.67$[A]
よって I[A]は
$I=(I_2-60)+(I_3-80)=29.3$[A]
答え (1)





