第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「電動機の制動と所要出力」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「電動機の制動と所要出力」の過去問題も解説しています。
- 電動機の始動と制動
- 各種電動機の所要出力
- 電験三種-機械の過去問解説:電動機の制動と所要出力
- 2000年(平成12年)問5
- 2000年(平成12年)問5 過去問解説
- 2002年(平成14年)問7
- 2002年(平成14年)問7 過去問解説
- 2006年(平成18年)問10
- 2006年(平成18年)問10 過去問解説
- 2009年(平成21年)問10
- 2009年(平成21年)問10 過去問解説
- 2010年(平成22年)問11
- 2010年(平成22年)問11 過去問解説
- 2012年(平成24年)問11
- 2012年(平成24年)問11 過去問解説
- 2015年(平成27年)問12
- 2015年(平成27年)問12 過去問解説
- 2016年(平成28年)問11
- 2016年(平成28年)問11 過去問解説
- 2017年(平成29年)問12
- 2017年(平成29年)問12 過去問解説
電動機の始動と制動
直流電動機の始動
直流電動機の始動は、始動電流を定格の 100~150[%]に制限するため電機子電圧を低くする必要があります。その方法として次のものがあります。
- 電機子回路の外部に抵抗を挿入する方法。
- 直流発電機の誘導起電力を制御して始動するワードレオナード方式およびサイリスタ電源による静止レオナード方式。
かご形誘導電動機の始動
かご形誘導電動機自体には、始動電流による制限はありませんが、始動電流による配電系統の電圧降下を防ぐために、減電圧始動が行われることがあります。
- 全電圧始動:電動機に直接全電圧を加えて始動する方法で、比較的小出力の電動機に用いられます。
- YーΔ始動:始動時には電動機一次巻線をY結線として、始動完了後にΔ結線に切り換える方法で、全電圧始動に比べて、始動電流,トルクは1/3になります。
- 始動補償器法:始動時に単相変圧器を用いて、そのタップを任意に選ぶことにより、50~80[%]程度の低い電圧で始動する方法で、始動完了後に全電圧に切り換えます。
- リアクトル始動:電動機一次回路に始動用リアクトルを挿入して、始動電流を制限する方法で、始動完了後にリアクトルを短絡します。
巻線形誘導電動機の始動
- 始動抵抗器法:始動時の二次回路にスリップリングを通して可変抵抗器を接続し、抵抗値により始動電流を制限する方法で、始動トルクは大きくとることができます。
同期電動機の始動
同期電動機は、それ自体で停止状態からの始動は不可能ですので、次の方法により始動します。
- 自己始動法:始動巻線を設けてかご形誘導電動機として始動する方法。
- 始動電動機法:他の電動機により同期速度付近まで回転速度を上昇させ、同期運転に入れる方法。
電気制動
- 回生制動:回転運動エネルギーを電気エネルギーに変換し、電源に送り返して制動トルクを得る方法。
- 発電制動:変換された電気エネル′ギーを外部に接続した制動抵抗で消費させ、制動トルクを得る方法。
- 逆転制動:直流電動機の電機子電圧の極性を反転させて制動トルクを得る方法。
- 逆相制動:かご形誘導電動機の相回転を逆転させて制動トルクを得る方法。
各種電動機の所要出力
ある負荷を負って安定に運転を継続するのに必要な電動機出力容量を所要出力といいます。電動機によって負荷を運転する場合、電動機トルクと負荷トルクとが平衡した点の速度で運転されますので、安定した運転状態を得るには電動機特性と同時に負荷の速度特性を知る必要があります。負荷の速度特性と速度動力特性を大別すると次の表のようになります。
| 負荷の種類 | 速度とトルクの関係 | 速度と動力の関係 | 負荷の例 |
| 定出力負荷 | T∝N-1 | P=一定 | 巻取機 定出力発電機 切削工作機 |
| 定トルク負荷 | T=一定 | P∝N | エレベータ コンベア |
| 2乗低減トルク負荷 | T∝N2 | P∝N3 | 渦巻ポンプ 送風機 |
電動機の所要出力はこのような負荷の特性を下に、各機器ごとに算出されます。
揚水ポンプの所要出力
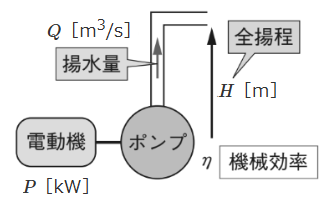
揚水ポンプとは、ポンプと電動機の2つを組み合わせた機器で、電力を加えて電動機を回し、電動機に直結したポンプが回ることにより水を押し上げる機械設備です。
全揚程 $H$[m]を毎秒 $Q$[m3/s]で揚水するとき、機械効率を $η$ 、余裕係数を $k$ とすると、ポンプ用電動機の所要出力 $P$[kW]は、次の式で表わすことができます。
ポンプ用電動機の所要出力を求める式
$P=\displaystyle\frac{9.8QHk}{η}$[kW]
$P$[kW]:電動機出力
$Q$[m3/s]:揚水量
$H$[m]:全揚程
$η$ : 機械効率
$k$: 余裕係数
巻き上げ機の所要出力
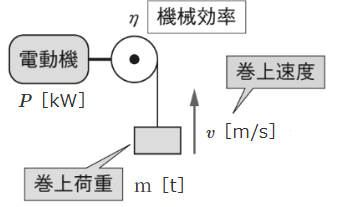
巻き上げ機は、電動機の回転力を利用して物体を上昇や下降させる機械設備で、クレーンや電気ホイスト、エレベーターなどのことをいいます。
質量 $m$[t]の物体を毎秒 $v$[m/s]の速度で巻き上げるとき、機械効率を $η$ 、余裕係数を $k$ とすると、巻き上げ機用電動機の所要出力 $P$[kW]は、次の式で表わすことができます。
巻き上げ機の所要出力を求める式
$P=\displaystyle\frac{9.8mvk}{η}$[kW]
$P$[kW]:巻き上げ機用電動機の所要出力
$m$[t]:巻上荷重
$v$[m/s]:巻上速度
$k$:余裕係数
$η$:機械効率
エレベーターの巻上荷重
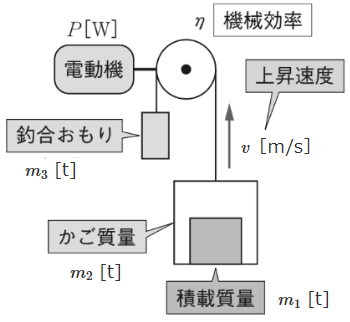
エレベーターは、電動機とつながった滑車が回ることによりワイヤーを巻き上げ、かごを上昇させます。エレベーターが満員の状態でかごを引き上げると、電動機に過大な負荷がかかるため、負荷を緩和する目的でかごの反対側に「釣り合いおもり」が吊り下げられています。
そのため、エレベーターの巻上荷重 $m$[t]は次の式で求めます。
エレベーターの巻上荷重を求める式
$m = m_1+m_2-m_3$
$m$[t]:巻上荷重
$m_1$ [t] :積載質量
$m_2$ [t] :かご質量
$m_3$ [t] :釣り合いおもりの質量
送風機の所要出力
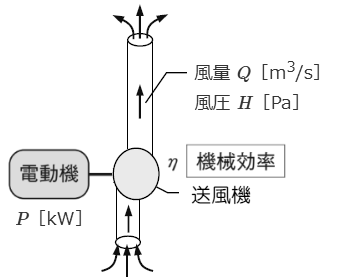
送風機は、ファンと電動機の2つを組み合わせたものであり、電力を加えて電動機を回し、電動機に直結したファンが回ることにより空気を押し出す機械設備です。
風圧 $H$[Pa]を毎秒 風量 $Q$[m3/s]で送風するとき、機械効率を $η$ 、余裕係数を $k$ とすると、送風機用電動機の所要出力 $P$[kW]は、次の式で表わすことができます。
送風機の所要出力を求める式
$P=\displaystyle\frac{QHk}{60000η}$
$P$[kW]:送風機用電動機の所要出力
$Q$[m3/s]:風量
$H$[Pa]:風圧
$k$:余裕係数
$η$:機械効率
風の動きを運動と考えた場合、次の法則が成り立ちます。
- 風車面を通過する空気の量(質量)は、風速の1乗に比例する
- 空気の運動エネルギーは、風速の2乗に比例する
- 風力発電の出力は、風速の3乗に比例する
この法則を回転速度 $N$ で考えると次のようになります。
- 風量 $Q$ は 回転速度 $N$ の1乗に比例する $Q∝N$
- 風圧 $H$ は 回転速度 $N$ の2乗に比例する $H∝N^2$
- トルク $T$ は 回転速度 $N$ の2乗に比例する $T∝N^2$
- 所要出力 $P$ は 回転速度 $N$ の3乗に比例する $P∝N^3$
減速機の所要出力
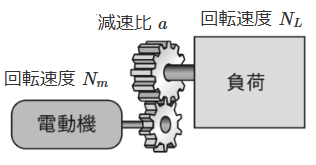
減速機は2つの歯車を組み合わせた構造になっている機器で、電動機で発生したトルクを増大させることができます。その代わりに負荷側の回転速度は下がります。電動機と負荷側の速度(及びトルク) の割合を表すものを 「減速比」 $a$ といいます。
電動機側の回転速度を $N_m$ としたときの負荷側の回転速度 $N_L$ は、次の式で表わすことができます。
減速機の回転速度を求める式
$N_L=\displaystyle\frac{N_m}{a}$
$N_L$[min-1]:負荷側の回転速度
$N_m$[min-1]:電動機側の回転速度
$a$:減速比
また、電動機側のトルクを $T_m$、効率を $η$ としたときの負荷側のトルク $T_L$ は、次の式で表わすことができます。
減速機のトルクを求める式
$T_L=T_m×η×a$
$T_L$[N・m]:負荷側のトルク
$T_m$[N・m]:電動機側のトルク
$a$:減速比
$η$:効率

電動機の出力を求める式
$P=Tω$
$P$[W]:電動機の出力
$T$[N・m]:電動機のトルク
$ω$[rad/s]:角速度
回転速度と角速度の関係式
$ω=2π×\displaystyle\frac{N}{60}$
$ω$[rad/s]:角速度
$N$[rpm または min-1]:回転速度
電験三種-機械の過去問解説:電動機の制動と所要出力
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
2000年(平成12年)問5
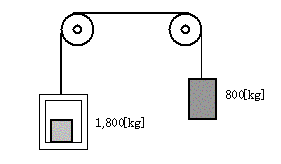
定格積載質量にかごの質量を加えた値が 1800[kg]、昇降速度が 2.5[m/s]、釣合いおもりの質量が 800[kg]のエレベータがある。このエレベータに用いる電動機の出力[kW]の値として、正しいのは次のうちどれか。
ただし、機械効率は 70[%]、加速に要する動力及びロープの質量は無視するものとする。
(1) 9 (2) 17 (3) 25 (4) 35 (5) 63
2000年(平成12年)問5 過去問解説
荷重を $W$[t]、昇降速度を $v$[m/s]、機械効率を $η$ 、余裕係数を $k$とすると、エレベータに用いる電動機の出力 $P$[kW]は、
$P=\displaystyle\frac{9.8Wvk}{η}$
$=\displaystyle\frac{9.8×(1.8-0.8)×2.5×1}{0.7}$
$=35$[kW]
答え (4)
2002年(平成14年)問7
面積 1[Km2]に降る 1時間あたり 60[mm]の降雨を貯水池に集め、これを 20台の同一仕様のポンプで均等に分担し、全揚程 12[m]を揚水して河川に排水する場合、各ポンプの駆動用電動機の所要出力[kW]の値として、最も近いのは次のうちどれか。
ただし、1時間当たりの揚水量は排水量に等しく、ポンプの効率は 0.82、設計製作上の余裕係数は 1.2とする。
(1) 96.5 (2) 143 (3) 492 (4) 600 (5) 878
2002年(平成14年)問7 過去問解説
面積 1[Km2]に降る 1時間あたり 60[mm]の降雨量は、面積×降水量で表すことができますので、
降雨量 = $1×(10^3)^2×60×10^{-3}=60×10^{3}$[m3]
ポンプ1台あたりの揚水量を $Q$[m3/s]とすると、
$Q=\displaystyle\frac{60×10^{3}}{20×3600}≒0.83$[m3 /s]
全揚程 $H$[m]を毎秒 $Q$[m3/s]で揚水するとき、ポンプの効率を $η$ 、余裕係数を $k$ とすると、ポンプ用電動機の所要出力 $P$[kW]は、
$P=\displaystyle\frac{9.8QHk}{η}$
$=\displaystyle\frac{9.8×0.83×12×1.2}{082}$
$≒143$[kW]
答え (2)
2006年(平成18年)問10
電動機で駆動するポンプを用いて、毎時 100[m3]の水を揚程 50[m]の高さに持ち上げる。ポンプの効率は 74[%]、電動機の効率は 92[%]で、パイプの損失水頭は 0.5[m]であり、他の損失水頭は無視できるものとする。このとき必要な電動機入力[kW]の値として、最も近いのはつぎのうちどれか。
(1) 18.4 (2) 18.6 (3) 20.2 (4) 72.7 (5) 74.1
2006年(平成18年)問10 過去問解説
全揚程 $H$[m]を毎秒 $Q$[m3/s]で揚水するとき、効率を $η$ 、余裕係数を $k$ とすると、ポンプ用電動機の所要出力 $P$[kW]は、
$P=\displaystyle\frac{9.8QHk}{η}$
$=\displaystyle\frac{9.8×\displaystyle\frac{100}{3600}×(50+0.5)×1}{0.74×0.92}$
$≒20.2$[kW]
答え (3)
2009年(平成21年)問10
誘導電動機によって回転する送風機のシステムで消費される電力を考える。
誘導電動機が商用交流電源で駆動されているときに送風機の風量を下げようとする場合、通風路にダンパなどを追加して流路抵抗を上げる方法が一般的である。ダンパの種類などによって消費される電力の減少量は異なるが、流路抵抗を上げ風量を下げるに従って消費される電力は若干減少する。このとき、例えば風量を最初の 50[%]に下げた場合に、誘導電動機の回転速度は( ア )。
一方、商用交流電源で直接駆動するのではなく、出力する交流の電圧 V と周波数 f との比( V / f )をほぼ一定とするインバータを用いて、誘導電動機を駆動する周波数を変化させ風量を調整する方法もある。この方法では、ダンパなどの流路抵抗を調整する手段は用いないものとする。このとき、機械的・電気的な損失などが無視できるとすれば、風量は回転速度の( イ )乗に比例し、消費される電力は回転速度の( ウ )乗に比例する。したがって、周波数を変化させて風量を最初の 50[%]に下げた場合に消費される電力は、計算上で( エ )[%]まで減少する。
商用交流電源で駆動し、ダンパなどを追加して風量を下げた場合の消費される電力の減少量はこれほど大きくはなく、インバータを用いると大きな省エネルギー効果が得られる。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句又は数値として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
|---|---|---|---|---|
| (1) | トルク変動に相当する滑り周波数分だけ変動する | 1 | 3 | 12.5 |
| (2) | 風量に比例して減少する | 1/2 | 3 | 12.5 |
| (3) | 風量に比例して減少する | 1 | 3 | 12.5 |
| (4) | トルク変動に相当する滑り周波数分だけ変動する | 1/2 | 2 | 25 |
| (5) | 風量に比例して減少する | 1 | 2 | 25 |
2009年(平成21年)問10 過去問解説
誘導電動機によって回転する送風機のシステムで消費される電力を考える。
誘導電動機が商用交流電源で駆動されているときに送風機の風量を下げようとする場合、通風路にダンパなどを追加して流路抵抗を上げる方法が一般的である。ダンパの種類などによって消費される電力の減少量は異なるが、流路抵抗を上げ風量を下げるに従って消費される電力は若干減少する。このとき、例えば風量を最初の 50[%]に下げた場合に、誘導電動機の回転速度は( トルク変動に相当する滑り周波数分だけ変動する )。
一方、商用交流電源で直接駆動するのではなく、出力する交流の電圧 V と周波数 f との比( V / f )をほぼ一定とするインバータを用いて、誘導電動機を駆動する周波数を変化させ風量を調整する方法もある。この方法では、ダンパなどの流路抵抗を調整する手段は用いないものとする。このとき、機械的・電気的な損失などが無視できるとすれば、風量は回転速度の( 1 )乗に比例し、消費される電力は回転速度の( 3 )乗に比例する。したがって、周波数を変化させて風量を最初の 50[%]に下げた場合に消費される電力は、計算上で( 12.5 )[%]まで減少する。
商用交流電源で駆動し、ダンパなどを追加して風量を下げた場合の消費される電力の減少量はこれほど大きくはなく、インバータを用いると大きな省エネルギー効果が得られる。
送風機の回転速度を変えた場合の性は次のような関係になります。
N:送風機の回転速度[min-1]
Q:風量[立方メートル/min]
H:圧力[MPa]
P:送風機のモータ駆動力[kW]
η:送風機効率
速度とトルクの関係より、
Q ∝ N ⇒ H ∝ N2
駆動力は、P = (H・Q)/η で表すことができますので、速度と動力の関係は、
P ∝ N3 ⇒ P ∝ Q3
と、モータの駆動力が送風機の回転速度、あるいは風量の3乗に比例する関係があります。
答え (1)
2010年(平成22年)問11
エレベータの昇降に使用する電動機の出力 P を求めるためには、昇降する実質の質量を
M[kg]、一定の昇降速度を v[m/min]、機械効率を η[%]とすると、
$P=9.8×M×\displaystyle\frac{v}{60}×( ア )×10^{-3}$
となる。ただし、出力 P の単位は[( イ )]であり、加速に要する動力及びロープの
質量は無視している。
昇降する実質の質量 M[kg]は、かご質量 MC[kg]と積載質量 ML[kg]とのかご側合
計質量と、釣合いおもり質量 MB[kg]との ( ウ ) から決まる。定格積載質量を Mn[kg]とすると、平均的に電動機の必要トルクが ( エ ) なるように、釣合いおもり質量 MB[kg]は、
MB=MC+α×Mn
とする。ただし、αは 1/3~1/2 程度に設計されることが多い。
電動機は、負荷となる質量 M[kg]を上昇させるときは力行運転、下降させるときは回
生運転となる。したがって、乗客がいない(積載質量がない)かごを上昇させるときは ( オ )運転となる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる語句,式又は単位として,正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | (オ) | |
|---|---|---|---|---|---|
| (1) | $\displaystyle\frac{100}{η}$ | kW | 差 | 小さく | 力行 |
| (2) | $\displaystyle\frac{η}{100}$ | kW | 和 | 大きく | 力行 |
| (3) | $\displaystyle\frac{100}{η}$ | kW | 差 | 小さく | 回生 |
| (4) | $\displaystyle\frac{η}{100}$ | W | 差 | 小さく | 力行 |
| (5) | $\displaystyle\frac{100}{η}$ | W | 和 | 大きく | 回生 |
2010年(平成22年)問11 過去問解説
エレベータの昇降に使用する電動機の出力 P を求めるためには、昇降する実質の質量を
M[kg]、一定の昇降速度を v[m/min]、機械効率を η[%]とすると、
$P=9.8×M×\displaystyle\frac{v}{60}×( $\displaystyle\frac{100}{η}$ )×10^{-3}$
となる。ただし、出力 P の単位は[( kW )]であり、加速に要する動力及びロープの
質量は無視している。
昇降する実質の質量 M[kg]は、かご質量 MC[kg]と積載質量 ML[kg]とのかご側合
計質量と、釣合いおもり質量 MB[kg]との ( 差 ) から決まる。定格積載質量を Mn[kg]とすると、平均的に電動機の必要トルクが ( 小さく ) なるように、釣合いおもり質量 MB[kg]は、
MB=MC+α×Mn
とする。ただし、αは 1/3~1/2 程度に設計されることが多い。
電動機は、負荷となる質量 M[kg]を上昇させるときは力行運転、下降させるときは回
生運転となる。したがって、乗客がいない(積載質量がない)かごを上昇させるときは ( 回生 )運転となる。
答え (3)
2012年(平成24年)問11
次の文章は、電動機の運転に関する記述である。
交流電源-整流器-平滑用コンデンサ-インバータで構成される回路によって電動機を駆動する場合、( ア )の大きな負荷を減速するときには、電動機からインバータに電力が流れ込む。
このとき直流電圧が上昇するので、( イ )とパワー半導体デバイスとの直列回路を平滑用コンデンサと並列に設け、パワー半導体デバイスをスイッチングして電流を調整することによって、電動機からの電力を消費させることができる。この方法を一般に( ウ )制動と呼んでいる。
一方、電力を消費するのではなく、逆変換できる整流器を介して交流電源に電力を戻し、他の用途などに有効に使うこともできる。この方法を一般に( エ )制動と呼んでいる。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
|---|---|---|---|---|
| (1) | 慣性モーメント | 抵抗 | 発電 | 回生 |
| (2) | 慣性モーメント | 抵抗 | 降圧 | 発電 |
| (3) | 摩擦係数 | 抵抗 | 降圧 | 発電 |
| (4) | 慣性モーメント | リアクトル | 発電 | 回生 |
| (5) | 摩擦係数 | リアクトル | 降圧 | 回生 |
2012年(平成24年)問11 過去問解説
交流電源-整流器-平滑用コンデンサ-インバータで構成される回路によって電動機を駆動する場合、( 慣性モーメント )の大きな負荷を減速するときには、電動機からインバータに電力が流れ込む。
このとき直流電圧が上昇するので、( 抵抗 )とパワー半導体デバイスとの直列回路を平滑用コンデンサと並列に設け、パワー半導体デバイスをスイッチングして電流を調整することによって、電動機からの電力を消費させることができる。この方法を一般に( 発電 )制動と呼んでいる。
一方、電力を消費するのではなく、逆変換できる整流器を介して交流電源に電力を戻し、他の用途などに有効に使うこともできる。この方法を一般に( 回生 )制動と呼んでいる。
答え (1)
2015年(平成27年)問12
毎分 5m3 の水を実揚程 10m のところにある貯水槽に揚水する場合、ポンプを駆動するのに十分と計算される電動機出力 P の値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、ポンプの効率は 80%、ポンプの設計、工作上の誤差を見込んで余裕をもたせる余裕係数は 1.1 とし、さらに全揚程は実揚程の1.05倍とする。また、重力加速度は 9.8m/s2 とする。
(1) 1.15 (2) 1.20 (3) 9.43 (4) 9.74 (5) 11.8
2015年(平成27年)問12 過去問解説
全揚程 $H$[m]を毎秒 $Q$[m3/s]で揚水するとき、効率を $η$ 、余裕係数を $k$ とすると、ポンプ用電動機の所要出力 $P$[kW]は、
$P=\displaystyle\frac{9.8QHk}{η}$
$=\displaystyle\frac{9.8×\displaystyle\frac{5}{60}×(10×1.05)×1.1}{0.8}$
$≒11.8$[kW]
答え (5)
2016年(平成28年)問11
かごの質量が 200kg、定格積載質量が 1000kg のロープ式エレベータにおいて、釣合いおもりの質量は、かごの質量に定格積載質量の 40% を加えた値とした。
このエレベータで、定格積載質量を搭載したかごを一定速度 90m/min で、上昇させるときに用いる電動機の出力の値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、機械効率は75%、加減速に要する動力及びロープの質量は無視するものとする。
(1) 1.20 (2) 8.82 (3) 11.8 (4) 23.5 (5) 706
2016年(平成28年)問11 過去問解説
荷重を $W$[t]、昇降速度を $v$[m/s]、機械効率を $η$ 、余裕係数を $k$とすると、エレベータに用いる電動機の出力 $P$[W]は、
$W=0.2+1-(0.2+1×0.4)=0.6$[t]
$P=\displaystyle\frac{9.8Wvk}{η}$
$=\displaystyle\frac{9.8×0.6×\displaystyle\frac{90}{60}×1}{0.75}$
$≒11.8$[kW]
答え (3)
2017年(平成29年)問12
次の文章は、送風機など電動機の負荷の定常特性に関する記述である。
電動機の負荷となる機器では、損失などを無視し、電動機の回転数と機器において制御対象となる速度が比例するとすると、速度に対するトルクの代表的な特性が以下に示すように二つある。
一つは、エレベータなどの鉛直方向の移動体で速度に対して( ア )トルク、もう一つは、空気や水などの流体の搬送で速度に対して( イ )トルクとなる特性である。
後者の流量制御の代表的な例は送風機であり、通常はダンパなどを設けて圧損を変化させて流量を制御するのに対し、ダンパなどを設けずに電動機で速度制御することでも流量制御が可能である。このとき、風量は速度に対して( ウ )して変化し、電動機に必要な電力は速度に対して( エ )して変化する特性が得られる。したがって、必要流量に絞って運転する機会の多いシステムでは、電動機で速度制御することで大きな省エネルギー効果が得られる。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
|---|---|---|---|---|
| (1) | 比例する | 2乗に比例する | 比例 | 3乗に比例 |
| (2) | 比例する | 一定の | 比例 | 2乗に比例 |
| (3) | 比例する | 一定の | 2乗に比例 | 3乗に比例 |
| (4) | 一定の | 2乗に比例する | 比例 | 3乗に比例 |
| (5) | 一定の | 2乗に比例する | 2乗に比例 | 2乗に比例 |
2017年(平成29年)問12 過去問解説
電動機の負荷となる機器では、損失などを無視し、電動機の回転数と機器において制御対象となる速度が比例するとすると、速度に対するトルクの代表的な特性が以下に示すように二つある。
一つは、エレベータなどの鉛直方向の移動体で速度に対して( 一定の )トルク、もう一つは、空気や水などの流体の搬送で速度に対して( 2乗に比例する )トルクとなる特性である。
後者の流量制御の代表的な例は送風機であり、通常はダンパなどを設けて圧損を変化させて流量を制御するのに対し、ダンパなどを設けずに電動機で速度制御することでも流量制御が可能である。このとき、風量は速度に対して( 比例 )して変化し、電動機に必要な電力は速度に対して( 3乗に比例 )して変化する特性が得られる。したがって、必要流量に絞って運転する機会の多いシステムでは、電動機で速度制御することで大きな省エネルギー効果が得られる。
答え (4)






