第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の機械科目に出題される「変圧器の並列結線」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の機械科目の試験で、実際に出題された「変圧器の並列結線」の過去問題も解説しています。
極性と端子記号
単相変圧器の一次巻線と二次巻線のおのおのの一端U,uを、図1に示すように接続し、一次巻線に任意の電圧を加える場合を考えます。一次巻線・二次巻線の巻き方向が図に示すようであれば、他の端子V,v間の電圧 $V_3$[V]は、一次電圧 $V_1$[V]と二次電圧 $V_2$[V]との差に等しい電圧 $V_1-V_2$[V]になります。これを減極性といいます。もし、U,uのかわりにU,vを接続し、V,u間の電圧を ${V_3}’$[V]とすれば、${V_3}’=V_1+V_2$[V]となります。これを加極性といいます。
このようなことがあるので、外部からでも極性がわかるように、変圧器の外箱には端子記号がつけてあります。この記号は、JIS C 4304に規定されており、高圧側(一次端子)にU,V、低圧側(二次端子)にu,vを用い、高圧端子から変圧器をみて右側にUをつけます。Uとuが外箱の同じ側にある変圧器が減極性、Uとuが対角線上にある変圧器が加極性であると定められています。なお、JISでは減極性を標準と規定しています。
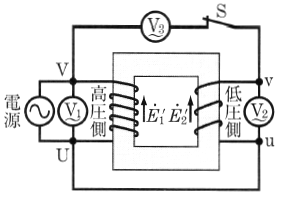
変圧器のつなぎ方(並行運転)
1台の変圧器から電力を供給している負荷設備において、負荷が増加したとき、変圧器の容量が不足することがあります。このような場合、増設負荷に応じられる容量の変圧器を新しく設置し、図2(a)に示すように、既設の変圧器と並列につないで使用します。これを並行運転といいます。
変圧器を並列につなぐ場合、図(a)のように、各変圧器の起電力の向きが同一になるように、すなわち極性が一致するようにつなぎます。もし、図(b)のように、二次側の各変圧器の起電力の向きが、反対になるようにつなぐと、二次側を短絡した状態になり、非常に大きな循環電流 $i$ が流れて、巻線を焼損することになります。
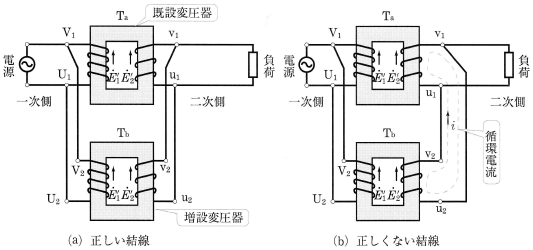
並行運転の条件
2台の変圧器を用いて並行運転をする場合、それぞれの変圧器に定格容量を超えない電流を分担させることが必要です。そのために必要な条件と理由は次のとおりです。
| 条件 | 理由 |
| ① 各変圧器の極性が一致していること | 極性が一致していないと、非常に大きな循環電流が流れて巻線を焼損する。 |
| ② 各変圧器の巻数比が等しいこと | 巻数比が異なると、循環電流が流れて巻線を過熱させる。 |
| ③ 各変圧器の巻線抵抗と漏れリアクタンスの比 r/x が等しいこと | r/x が等しくないと、各変圧器に流れる電流に位相差を生じ、取り出せる電力は各変圧器の出力の和より小さくなり、出力に対する銅損の割合が大きくなって利用率が悪くなる。 |
| ④ 各変圧器の百分率インピーダンス降下が等しいこと。 | 各変圧器が定格出力に比例する電流を分担するために必要である。 |
なお、三相変圧器の並行運転の場合は、上の①~④のほかに、さらに次のような条件が必要です。
⑤ 相回転が一致していること。
⑥ 一次側,二次側の線間誘導起電力の角変位が等しいこと。
各変圧器の励磁電流を無視し、一次側を二次側に換算した図3(a)の簡易等価回路で、各変圧器のインピーダンスに流れる分担電流を $I_{2a}$[A],$I_{2b}$[A]とすると、インピーダンス降下は $I_{2a}Z_{21a}=I_{2b}Z_{21b}$ ですので、
$\displaystyle\frac{I_{2a}}{I_{2b}}=\displaystyle\frac{Z_{21b}}{Z_{21a}}$
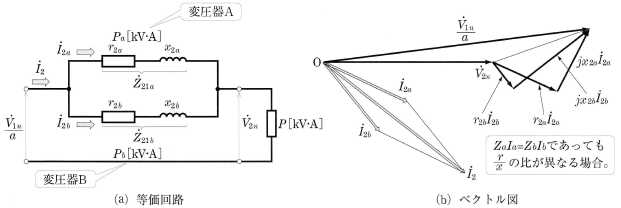
各変圧器の二次定格電圧を $V_{2n}$、二次定格電流を $I_{2A}$[A],$I_{2B}$[A]とすると、各変圧器の百分率インピーダンス降下 $z_a$[%],$z_b$[%]は、次の式で与えられます。
$z_a=\displaystyle\frac{I_{2A}Z_{21a}}{V_{2n}}×100$
$z_b=\displaystyle\frac{I_{2B}Z_{21b}}{V_{2n}}×100$
これより
$\displaystyle\frac{I_{2a}}{I_{2b}}=\displaystyle\frac{Z_{21b}}{Z_{21a}}=\displaystyle\frac{z_{b}I_{2A}}{z_{a}I_{2B}}$
$\displaystyle\frac{I_{2a}}{I_{2b}}=\displaystyle\frac{Z_{21b}}{Z_{21a}}=\displaystyle\frac{I_{2a}V_{2n}}{I_{2b}V_{2n}}=\displaystyle\frac{z_{b}(I_{2A}V_{2n})}{z_{a}(I_{2B}V_{2n})}$
$I_{2a}V_{2n}=P_a$,$I_{2b}V_{2n}=P_b$は変圧器が供給している電力であって、$I_{2A}V_{2n}=P_A$,$I_{2B}V_{2n}=P_B$は定格容量とすると、
$\displaystyle\frac{P_a}{P_b}=\displaystyle\frac{\displaystyle\frac{P_A}{Z_a}}{\displaystyle\frac{P_B}{Z_b}}$ … (2)
負荷電力を $P=P_a+P_b$ とすると、各変圧器の電力、すなわち分担する負荷 $P_a$,$P_b$ は、次の式で与えられます。
変圧器 A、Bが分担する負荷を求める式
$P_a=P×\displaystyle \frac{ \displaystyle \frac{ P_{A} }{ z_a } }{ \displaystyle \frac{ P_{A} }{ z_a}+\displaystyle \frac{ P_{B} }{ z_b } }$
$P_b=P×\displaystyle \frac{ \displaystyle \frac{ P_{B} }{ z_b } }{ \displaystyle \frac{ P_{A} }{ z_a }+\displaystyle \frac{ P_{B} }{ z_b } }$
$P_a$,$P_b$:分担する負荷
$P_A$[V・A]:変圧器Aの定格容量
$P_B$[V・A]:変圧器Bの定格容量
$z_a$[%]:変圧器Aの百分率インピーダンス降下
$z_b$[%]:変圧器Bの百分率インピーダンス降下
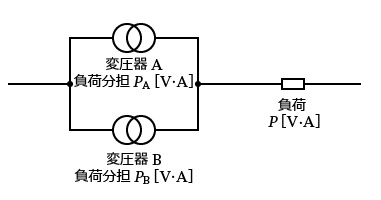
$z_a=z_b$ のとき、各変圧器は定格負荷の状態で容量比に比例した負荷分担をすることができます。また、変圧器が3台以上の場合でもこの関係は成り立ちます。
電験三種-機械の過去問解説:変圧器の並列結線
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の機械科目で出題された問題です。
1999年(平成11年)問10
下表は、電力用変圧器の並列運転を行うために必要とする条件と目的をまとめたものである。
| 必 要 条 件 | 目 的 |
| 各変圧器の( ア )が等しいこと。 | 各変圧器に( イ )電流を流さない。 |
| 各変圧器の百分率短絡インピーダンス(百 分率インピーダンス降下)が等しいこと。 | 各変圧器の定格容量に比例して( ウ ) 電流を分担させる。 |
| 各変圧器の巻線抵抗と漏れリアクタンスの ( エ )が等しいこと。 | 各変圧器の分担電流を同相とし、取り出せ る出力を最大とする。 |
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に記入する字句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 巻線比 | 循環 | 励磁 | 値 |
| (2) | 巻線比 | 循環 | 負荷 | 比 |
| (3) | 入力電圧 | 短絡 | 負荷 | 値 |
| (4) | 巻線比 | 短絡 | 負荷 | 値 |
| (5) | 入力電圧 | 循環 | 励磁 | 比 |
1999年(平成11年)問10 過去問解説
| 必 要 条 件 | 目 的 |
| 各変圧器の( 巻線比 )が等しいこと。 | 各変圧器に( 循環 )電流を流さない。 |
| 各変圧器の百分率短絡インピーダンス(百 分率インピーダンス降下)が等しいこと。 | 各変圧器の定格容量に比例して( 負荷 ) 電流を分担させる。 |
| 各変圧器の巻線抵抗と漏れリアクタンスの ( 比 )が等しいこと。 | 各変圧器の分担電流を同相とし、取り出せ る出力を最大とする。 |
答え (2)
2000年(平成12年)問3
定格電圧及び巻数比が等しい2台の変圧器A,Bがある。それらの変圧器の定格容量はそれぞれ 30[kVA],20[kVA]であり、短絡インピーダンスはそれぞれ 5[Ω],10[Ω]である。これら2台の変圧器を並列に接続して、いずれも過負荷にならないように稼働させるとき、二次側に加えることができる最大負荷[kVA]の値として、正しいのは次のうちどれか。
ただし、各変圧器の巻線の抵抗と漏れリアクタンスの比は等しいものとする。
(1) 30 (2) 35 (3) 40 (4) 45 (5) 50
2000年(平成12年)問3 過去問解説
A,B変圧器の定格容量を $P_A$[kVA],$P_B$[kVA]、分担負荷を $P_a$[kVA],$P_b$[kVA]、短絡インピーダンスを $Z_a$[Ω],$Z_b$[Ω]とすると、
$\displaystyle\frac{P_a}{P_b}=\displaystyle\frac{Z_b}{Z_a}$
$P_b=\displaystyle\frac{P_AZ_a}{Z_b}$
短絡インピーダンスが小さいA変圧器の負荷分担が $P_a=P_A$ に達したとき、両変圧器で分担できる最大負荷 $P_m$[kVA]になりますので、
$P_m=P_a+P_b=P_A+\displaystyle\frac{P_AZ_a}{Z_b}=30+\displaystyle\frac{30×5}{10}=45$[kVA]
答え (4)
2002年(平成14年)問4
変圧器の特性とは、その端子に現われる誘導起電力の相対的方向を表したものである。単相変圧器において、一次側記号をU及びV、二次側記号をu及びvとすれば、Uとuが外箱の同じ側にある変圧器は( ア )、対角線上にある変圧器は( イ )である。
2台の変圧器を並列に接続して運転する場合、これらの変圧器の一次巻線及び二次巻線について、それぞれの極性が同一となるように接続しなければならない。もし、いずれかの巻線で誤って逆の接続をすると、2台の変圧器の二次電圧の起電力が二次巻線によって形成される( ウ )で同方向・直列に接続されることになる。この場合、巻線のインピーダンスは小さいので、非常に大きな( エ )電流が流れて巻線が焼損する。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に記入する語句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | 減極性 | 加極性 | 閉開路 | 循環 |
| (2) | 減極性 | 加極性 | 並列回路 | 負荷 |
| (3) | 加極性 | 減極性 | 閉開路 | 循環 |
| (4) | 加極性 | 減極性 | 並列回路 | 循環 |
| (5) | 加極性 | 減極性 | 直列開路 | 負荷 |
2002年(平成14年)問4 過去問解説
変圧器の特性とは、その端子に現われる誘導起電力の相対的方向を表したものである。単相変圧器において、一次側記号をU及びV、二次側記号をu及びvとすれば、Uとuが外箱の同じ側にある変圧器は( 減極性 )、対角線上にある変圧器は( 加極性 )である。
2台の変圧器を並列に接続して運転する場合、これらの変圧器の一次巻線及び二次巻線について、それぞれの極性が同一となるように接続しなければならない。もし、いずれかの巻線で誤って逆の接続をすると、2台の変圧器の二次電圧の起電力が二次巻線によって形成される( 閉開路 )で同方向・直列に接続されることになる。この場合、巻線のインピーダンスは小さいので、非常に大きな( 循環 )電流が流れて巻線が焼損する。
図1は減極性、 図2は加極性、 図3は並行運転の結線図です。減極性の変圧器と加極性の変圧器を並行運転すると、二次側が閉回路となって、大きな循環電流 I[A]が流れて巻線が焼損します。
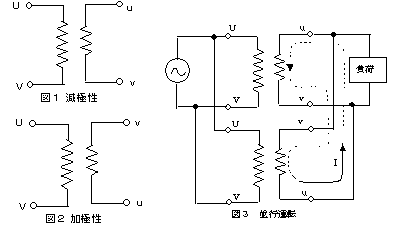
答え (1)
2003年(平成15年)問7
電力用単相二巻線変圧器に関する記述として、誤っているのは次のうちどれか。
- 定格容量とは、定格二次電圧、定格周波数及び定格力率において、指定された温度上昇の限度を超えることなく、二次端子間に得られる皮相電力である。
- 定格負荷状態において、二次端子電圧が定格二次電圧になるように一次端子間に加える電圧は、定格一次電圧に等しい。
- 変圧比とは、二次巻線を基準とした、二つの巻線の無負荷時における電圧の比である。
- 全損失は、無負荷損と負荷損の和である。
- 変圧比が等しく定格容量が異なる2台の変圧器を並列運転する場合、2台の百分率短絡インピーダンスが等しければ、負荷はそれぞれの変圧器の定格容量の比に分配される。
2003年(平成15年)問7 過去問解説
定格負荷状態において、二次端子電圧が定格二次電圧になるように一次端子間に加える電圧は、巻線抵抗による電圧降下を考慮して、定格一次電圧より高い電圧を加えます。したがって、(2)の記述が誤りです。
答え (2)
2012年(平成24年)問8
三相変圧器の並行運転に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- 各変圧器の極性が一致していないと、大きな循環電流が流れて巻線の焼損を引き起こす。
- 各変圧器の変圧比が一致していないと、負荷の有無にかかわらず循環電流が流れて巻線の過熱を引き起こす。
- 一次側と二次側との誘導起電力の位相変位(角変位)が各変圧器で等しくないと、その程度によっては、大きな循環電流が流れて巻線の焼損を引き起こす。したがって、Δ-YとY-Yとの並行運転はできるが、Δ-ΔとΔ-Yとの並行運転はできない。
- 各変圧器の巻線抵抗と漏れリアクタンスとの比が等しくないと、各変圧器の二次側に流れる電流に位相差が生じ取り出せる電力は各変圧器の出力の和より小さくなり、出力に対する銅損の割合が大きくなって利用率が悪くなる。
- 各変圧器の百分率インピーダンス降下が等しくないと、各変圧器が定格容量に応じた負荷を分担することができない。
2012年(平成24年)問8 過去問解説
一次側と二次側との誘導起電力の位相変位(角変位)が各変圧器で等しくないと、その程度によっては、大きな循環電流が流れて巻線の焼損を引き起こします。Δ-Yの角偏位は30°で、Δ-ΔとY-Yの角偏位は0°です。Δ-YとY-Yとの並行運転はできません。したがって、(3)の記述が誤りです。
答え (3)






