第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される「トランジスタ増幅回路」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された「トランジスタ増幅回路」の過去問題も解説しています。
トランジスタ増幅回路
増幅回路とは、「少ない電流を入力して大きな出力電流を得る回路」や、「少ない電圧を入力して大きな出力電圧を得る回路」などのように、小さな入力によって大きな出力を得るための回路です。
基本的なトランジスタ増幅回路
トランジスタを使った増幅回路を接地方法で分けると、「エミッタ接地」「ベース接地」「コレクタ接地」の3つの方式があります。
エミッタ接地回路
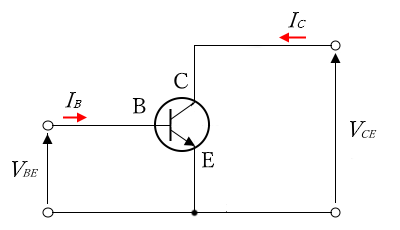
エミッタ接地回路は、バイポーラトランジスタのエミッタを入出力共通端子として、ベースを入力、コレクタを出力として使う増幅回路です。
エミッタ共通回路、エミッタコモン回路とも呼ばれます。
ベース接地回路
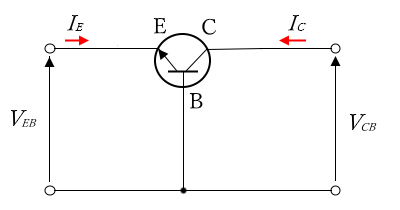
ベース接地回路は、バイポーラトランジスタのベースを入出力共通端子とし、エミッタを入力、コレクタを出力として使う回路です。
電圧増幅率が高く、電流増幅作用がない(1倍)という特徴があります。
ベース共通回路、ベースコモン回路とも呼ばれます。
コレクタ接地回路
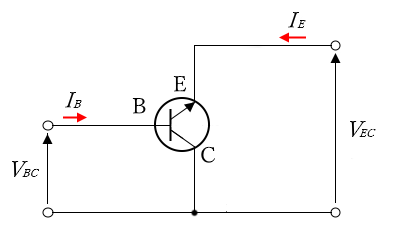
コレクタ接地回路は、バイポーラトランジスタのコレクタを入出力共通端子とし、ベースを入力、エミッタを出力として使う回路です。
電流増幅率が高く、電圧増幅作用がない(1倍)という特徴を持ちます。
出力(エミッタ)が入力電圧に追従することから、「エミッタフォロワ」とも呼ばれます。
電流増幅率
電流増幅率とは入力電流に対する出力電流の割合を表したものです。電流増幅率が大きければ、少ない入力電流で大きな出力電流が得られることを意味します。
ベース接地回路の入力電流と出力電流は等しく、電流増幅率は1倍となり、電流を増幅しないことを意味しています。
$電流増幅率=\displaystyle\frac{出力電流}{入力電流}$
電圧増幅率
電圧増幅率とは入力電圧に対する出力電圧の割合を表したものです。電圧増幅率が大きければ、少ない入力電圧で大きな出力電圧を得られることを意味します。
コレクタ接地回路の入力電圧と出力電圧は等しく、電圧増幅率は1倍となり、電圧を増幅しないことを意味しています。
$電圧増幅率=\displaystyle\frac{出力電圧}{入力電圧}$
トランジスタの静特性
トランジスタの各部の電圧、電流の相互関係を調べたものを特性といい、トランジスタを直流回路で使う場合の特性をまとめたものを「静特性」といいます。

図のようなエミッタ接地トランジスタを動作させたときの、トランジスタの入力と出力の関係を表します。
入力:電流 $I_B$ 、電圧 $V_{BE}$
出力:電流 $I_C$ 、電圧 $V_{CE}$
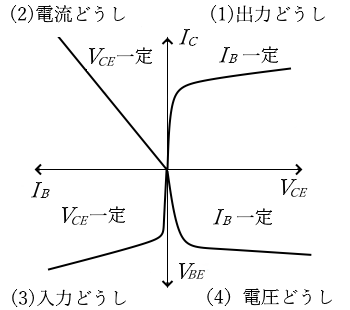
(1) 出力どうしの関係
入力電流 $I_B$ は一定として考えています。
(2) 電流どうしの関係
出力電圧 $V_{CE}$ は一定として考えています。
(3) 入力どうしの関係
出力電圧 $V_{CE}$ は一定として考えています。
(4) 電圧どうしの関係
入力電流 $I_B$ は一定として考えています。
hパラメータ
トランジスタは、特性曲線のある一部の領域内で動作させるのが一般的です。この場合、特性曲線を直線とみなすことができます。したがって、特性曲線のすべてを知らなくても直線の傾きがわかればトランジスタの動作特性を考えることができます。
このための、入力と出力の関係を4つの値で示したものを「hパラメータ」といい、入力インピーダンス($h_{ie}$)、電圧帰還率($h_{re}$)、電流増幅率($h_{fe}$)、出力アドミタンス($h_{oe}$)の4種類があります。
図は、エミッタ接地トランジスタの特性曲線を示しています。

入力インピーダンス $h_{ie}$
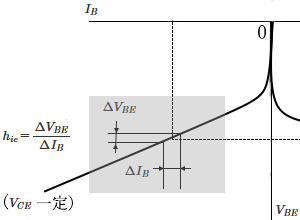
$V_{BE}$ー$I_B$ 特性の傾き $h_{ie}$ は、トランジスタの出力をショートした場合の入力インピーダンスを示す定数です。単位はΩで表します。
$h_{ie}=\displaystyle\frac{ΔV_{BE}}{ΔI_B}$ [Ω]
電圧帰還率 $h_{re}$
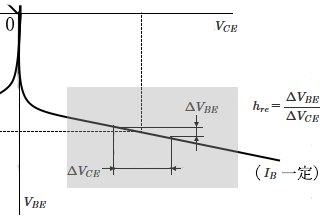
$V_{CE}$ー$V_{BE}$ 特性の傾き $h_{re}$ は、電圧帰還率と呼ばれる定数です。単位はありません。
$h_{re}=\displaystyle\frac{ΔV_{BE}}{ΔV_{CE}}$
電流増幅率 $h_{fe}$
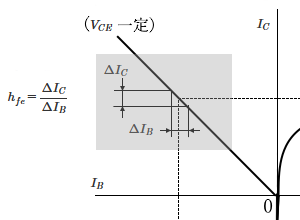
$I_B$ー$I_C$ 特性の傾き $h_{fe}$ は、トランジスタの電流増幅率を示す定数です。単位はありません。
$h_{fe}=\displaystyle\frac{ΔI_C}{ΔI_B}$
出力アドミタンス $h_{oe}$
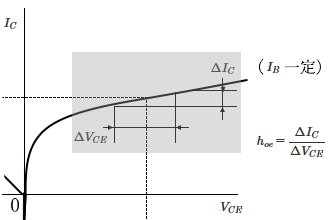
$V_{CE}$ー$I_C$ 特性の傾き $h_{oe}$ は、トランジスタの入力をオープンにした場合の出力アドミタンスを示す定数です。単位はS(ジーメンス)で表します。
$h_{oe}=\displaystyle\frac{ΔI_C}{ΔV_{CE}}$ [S]
エミッタ接地トランジスタの入力インピーダンス($h_{ie}$)、電圧帰還率($h_{re}$)、電流増幅率($h_{fe}$)、出力アドミタンス($h_{oe}$)を求める式
$h_{ie}=\displaystyle\frac{ΔV_{BE}}{ΔI_B}$ [Ω]
$h_{re}=\displaystyle\frac{ΔV_{BE}}{ΔV_{CE}}$
$h_{fe}=\displaystyle\frac{ΔI_C}{ΔI_B}$
$h_{oe}=\displaystyle\frac{ΔI_C}{ΔV_{CE}}$ [S]
増幅度
入力信号と出力信号の比を「増幅度」といいます。電圧増幅度を $A_v$,電流増幅度を $A_i$,電力増幅度を $A_p$ とすると、それぞれの増幅度は次の式で計算することができます。
増幅度を求める公式
$A_v=\left|\displaystyle\frac{v_o}{v_i}\right|$,$A_i=\left|\displaystyle\frac{i_o}{i_i}\right|$ ,$A_p=\left|\displaystyle\frac{P_o}{P_i}\right|=A_v×A_i$
$A_v$:電圧増幅度
$A_i$:電流増幅度
$A_p$:電力増幅度
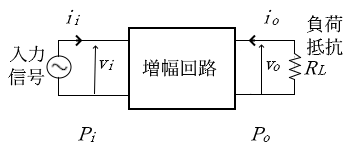
増幅度と利得
増幅度をデシベル[dB]の単位で表したものを「利得」といいます。デシベル[dB]とは、ある特定の基準に対しての大きさ(相対値)を表す単位です。「倍率」と「dB」の間には次の関係があります。
| 倍率 | 1倍 | 10倍 | 100倍 | 1000倍 | 10000倍 | 100000倍 |
| デシベル | 0db | 20db | 40db | 60db | 80db | 100db |
以上のように、倍率の「0」が1つ増えるごとに「20dB」ずつ増える、といった関係にあります。例えば「10000000000 倍」 を 「dB」 に変換すると 200 dB という小さい数字になり、大きな倍数を表す時に便利な単位になります。
増幅度と利得の合成
増幅度と利得の合成
n個の増幅回路を縦続(カスケード)接続した場合の全体の増幅度 $A$ と利得 $G$ は、次の式で計算することができます。
$A=A_1×A_2×A_3×…×A_n$
$G=G_1+G_2+G_3+…+G_n$ [dB]
$A$:増幅度
$G$:利得
100倍増幅できるトランジスタ①と、1000倍 増幅できるトランジスタ②の「増幅度」と「利得」の計算をしてみます。
100倍 増幅できるトランジスタ①の増幅度は 100、 利得は 40dB です。
1000倍 増幅できるトランジスタ②の増幅度は 1000、利得は 60dB です。
それでは、トランジスタ① とトランジスタ② の 増幅度 と 利得 をそれぞれ合成してみます。
増幅度の合成は「積」で求められる → 100 × 1000 = 100000… 合成増幅度は 100000
利得の合成は「和」で求められる → 40dB + 60dB = 100dB … 合成利得は 100dB
トランジスタ① とトランジスタ② の合成増幅度は100000 、合成利得は 100dB となります。
hパラメータを用いて求める
増幅度は、hパラメータを用いて求めることもできます。次の図は、エミッタ接地増幅回路における電流と電圧の変化量を記号で示しています。
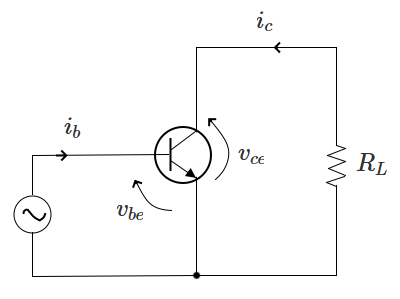
入力インピーダンス($h_{ie}$)、電流増幅率($h_{fe}$)を求める公式より
$h_{ie}=\displaystyle\frac{v_{be}}{i_b}$ ⇒ $i_b=\displaystyle\frac{v_{be}}{h_{ie}}$ … (1)
$h_{fe}=\displaystyle\frac{i_c}{i_b}$ ⇒ $i_c=h_{fe}×i_b$ …(2)
$v_{ce}=-i_c×R_L$ … (3)
式(1)を式(2)に代入します。
$i_c=h_{fe}×\displaystyle\frac{v_{be}}{h_{ie}}$ … (4)
式(4)を式(3)に代入します。
$v_{ce}=-h_{fe}×\displaystyle\frac{v_{be}}{h_{ie}}×R_L$
したがって、電圧増幅度 $A_v$ は、
$A_v=\left|\displaystyle\frac{v_o}{v_i}\right|=\left|\displaystyle\frac{v_{ce}}{v_{be}}\right|=\left|\displaystyle\frac{-h_{fe}}{h_{ie}}×R_L\right|$
利得を求める公式
電圧利得、電流利得、電力利得を求める式
電圧利得を $G_v$、電流利得を $G_i$、電力利得を $G_p$ とすると、それぞれの利得は次の式で計算することができます。
$G_v=20log_{10}A_v$ [dB]
$G_i=20log_{10}A_i$ [dB]
$G_p=10log_{10}A_p$ [dB]
$A_v$:電圧増幅度
$A_i$:電流増幅度
$A_p$:電力増幅度
電験三種-理論の過去問解説:トランジスタ増幅回路
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1997年(平成9年)問13【電験理論の過去問題】
図はあるエミッタ接地トランジスタの静特性を示す。この特性より、ベース電流 $I_B=40$ [μA] 、コレクタ・エミッタ間の電圧 $V_{CE}=6$ [V] における電流増幅率β(又は $h_{fe}$)及び出力抵抗 $r_o$ [Ω] の値として、正しいものを組み合わせたのものは次のうちどれか。
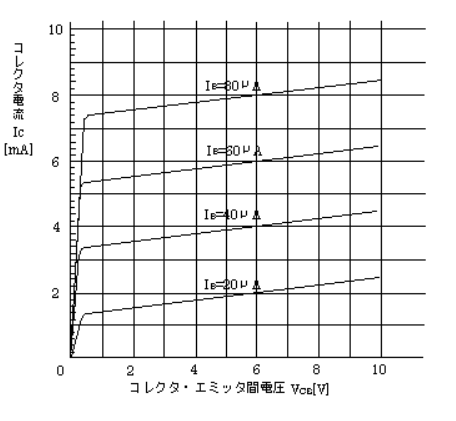
- β=80 $r_o$=30000
- β=100 $r_o$=10000
- β=100 $r_o$=20000
- β=200 $r_o$=10000
- β=200 $r_o$=20000
$V_{CE}=6$ [V]、$I_B=40$ [μA] のとき、
$I_C=4$ [mA]
$V_{CE}=6$ [V]、$I_B=60$ [μA]のとき、
$I_C=6$ [mA]
ですので、電流増幅率$β$は、
$β=\displaystyle\frac{ΔI_C}{ΔI_B}=\displaystyle\frac{(6-4)×10^{-3}}{(60-40)×10^{-6}}=100$
$I_B=40$ [μA]、$V_{CE}=6$ [V]のとき、
$I_C=4$ [mA]
$I_B=40$ [μA]、$V_{CE}=4$ [V]のとき、
$I_C=3.8$ [mA]
ですので、出力抵抗 $r_o$ [Ω] は、
$r_o=\displaystyle\frac{ΔV_{CE}}{ΔI_C}=\displaystyle\frac{6-4}{(4-3.8)×10^{-3}}=10000$ [Ω]
答え (2)
1998年(平成10年)問13【電験理論の過去問題】
図のようなトランジスタ増幅回路において、入力側の電圧 $v_i=0.2$ [V]、電流 $i_i=40$ [μA] であるとき、出力側の電圧 $v_o=5$ [V]、電流 $i_o=4$ [mA] であった。この増幅回路の電力利得 [dB] の値として、正しいのは次のうちどれか。ただし、log102=0.30、log103=0.477、log105=0.699 とする。
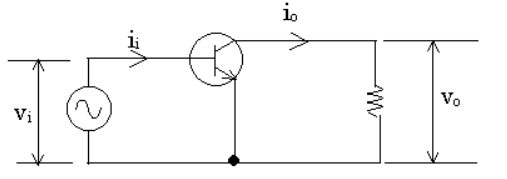
(1) 16 (2) 25 (3) 34 (4) 43 (5) 52
入力電力を $P_i=v_ii_i$、出力電力を $P_i=v_oi_o$ とすると、電力増幅度 $A_p$ は、
$A_p=\left|\displaystyle\frac{P_o}{P_i}\right|=\left|\displaystyle\frac{v_oi_o}{v_ii_i}\right|=\left|\displaystyle\frac{5×4×10^{-3}}{0.2×40×10^{-6}}\right|=2500$
電力利得を $G_p$ [dB] とすると、
$\begin{eqnarray}G_p&=&10log_{10}A_p\\&=&10log_{10}2500\\&=&10log_{10}(5^2×10^2)\\&=&10(2log_{10}5+2)\\&=&10(2log_{10}\displaystyle\frac{10}{2}+2)\\&=&10(2(log_{10}10-log_{10}2)+2)\\&=&10(2(1-0.3)+2)\\&=&10×3.4=34 [dB] \end{eqnarray}$
答え (3)
2000年(平成12年)問7【電験理論の過去問題】
次のようなブロック図で示す2つの増幅器を継続接続した回路があり、増幅器1の電圧増幅度は 10 である。いま入力電圧 $V_1$ の値として 0.4 [mV] の信号を加えたとき、出力電圧 $V_o$ の値は 0.4 [V] であった。増幅器2の電圧利得 [dB] の値として、正しいのは次のうちどれか。

(1) 10 (2) 20 (3) 40 (4) 50 (5) 60
増幅器1の出力電圧を $V_{1o}$ [V] とすると、
$A_v=\left|\displaystyle\frac{V_{1o}}{V_{1}}\right|$
$10=\left|\displaystyle\frac{V_{1o}}{0.4×10^{-3}}\right|$
$V_{1o}=10×0.4×10^{-3}=0.4×10^{-2}$ [V]
増幅器2の電圧利得 $G_{2v}$ [dB] は、
$\begin{eqnarray}G_{2v}&=&20log_{10}A_{2v}\\&=&20log_{10}\displaystyle\frac{V_{o}}{V_{1o}}\\&=&20log_{10}\displaystyle\frac{0.4}{0.4×10^{-2}}\\&=&20log_{10}\displaystyle\frac{1}{10^{-2}}\\&=&20log_{10}10^2\\&=&20×2log_{10}10\\&=&20×2×1=40 [dB] \end{eqnarray}$
答え (3)
2004年(平成16年)問18【電験理論の過去問題】
図のようなトランジスタ増幅器がある。次の(a)及び(b)に答えよ。
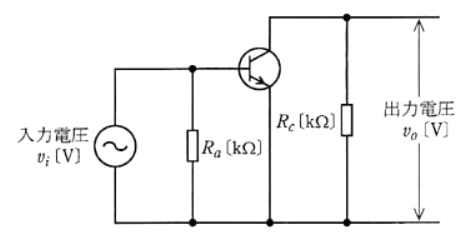
(a) 次の文章はトランジスタ増幅器について述べたものである。
図の回路は( ア )形のトランジスタの( イ )を接地した増幅回路を、交流信号に注目して示している。入力電圧と出力電圧の瞬時値をそれぞれ $v_i$ [V] 及び $v_o$ [V] とすると、この回路では $v_i$ に対して $v_o$ は、位相が( ウ )ずれる。このときの入力電圧と出力電圧の実効値をそれぞれ $V_i$ [V] 及び $V_o$ [V] とすると、電圧利得は( エ )[dB] の式で表される。
上記の記述の空欄箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句、式又は数値として、正しいものを組合せたのは次のうちどれか。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | npn | エミッタ | 180° | 20log10(Vo/Vi) |
| (2) | pnp | コレクタ | 180° | 20log10(Vi/Vo) |
| (3) | npn | エミッタ | 90° | 20log10(Vo/Vi) |
| (4) | pnp | コレクタ | 90° | 20log10(Vi/Vo) |
| (5) | npn | エミッタ | 90° | 10log10(Vo/Vi) |
(b) 図示された増幅回路の抵抗が $R_a=25$ [kΩ]、$R_c=20$ [kΩ] で、入力電圧を加えたとき、この回路の電圧利得 [dB] の値として、最も近いのは次のうちどれか。
ただし、トランジスタの電流増幅率 $h_{fe}=120$ 、ベース-エミッタ間の抵抗 $h_{ie}=2$ [kΩ]、log102=0.301、log103=0.477とする。
(1) 2800 (2) 1120 (3) 832 (4) 102 (5) 62
(a) 図の回路は( npn )形のトランジスタの( エミッタ )を接地した増幅回路を、交流信号に注目して示している。入力電圧と出力電圧の瞬時値をそれぞれ $v_i$ [V] 及び $v_o$ [V] とすると、この回路では $v_i$ に対して $v_o$ は、位相が( 180° )ずれる。このときの入力電圧と出力電圧の実効値をそれぞれ $V_i$ [V] 及び $V_o$ [V] とすると、電圧利得は( 20log10(Vo/Vi) ) [dB] の式で表される。
答え (1)
(b) 入力電流を $i_i$ [A]、出力電流を $i_o$ [A] とすると、電圧増幅率 $A_v$ は、
$\begin{eqnarray}A_v&=&\left|\displaystyle\frac{v_o}{v_i}\right|=\left|\displaystyle\frac{i_oR_c}{i_iR_a}\right|=\left|\displaystyle\frac{i_ih_{fe}R_c}{i_iR_a}\right|=\left|\displaystyle\frac{h_{fe}R_c}{R_a}\right|\\&=&\left|\displaystyle\frac{120×20×10^3}{25×10^3}\right|=96\end{eqnarray}$
電圧利得 $G_v$ [dB] は、
$\begin{eqnarray}G_v&=&20log_{10}A_v\\&=&20log_{10}96\\&=&20log_{10}(4^2×6)\\&=&20×4×log_{10}6\\&=&80log_{10}(2×3)\\&=&80(log_{10}2+log_{10}3)\\&=&80(0.301+0.477)≒62 [dB] \end{eqnarray}$
答え (5)
2008年(平成20年)問13【電験理論の過去問題】
トランジスタの接地方式の異なる基本増幅回路を図 1 、図 2 及び図 3 に示す。以下の a 〜 d に示す回路に関する記述として、正しいものを組み合わせたのは次のうちどれか。
- 図 1 の回路では、入出力信号の位相差は 180 [°] である。
- 図 2 の回路は、エミッタ接地増幅回路である。
- 図2の回路は、エミッタホロワとも呼ばれる。
- 図3の回路で、エミッタ電流及びコレクタ電流の変化分の比 $\displaystyle\frac{ΔI_C}{ΔI_E} $ の値は、約100である。
ただし、$I_B$、$I_C$、$I_E$ は直流電流、$v_i$、$v_o$ は入出力信号、$R_L$ は負荷抵抗、$V_{BB}$、$V_{CC}$ は直流電源を示す。
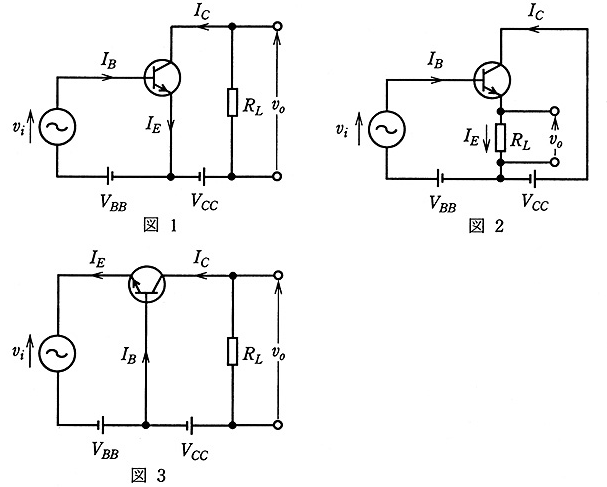
(1) aとb (2) aとc (3) aとd (4) bとd (5) cとd
図 1はエミッタ接地方式、図 2はコレクタ接地方式、図 3はベース接地方式です。
- 図 1 のエミッタ接地方式では、コレクタ側から出力を取り出しているので位相は180 [°] ずれます。(正しい)
- 図 2 の回路は、コレクタ接地方式です。(誤り)
- 図 2 のコレクタ接地方式は、エミッタホロワとも呼ばれます。(正しい)
- 図3のベース接地方式では、エミッタ電流及びコレクタ電流の変化分の比 $\displaystyle\frac{ΔI_C}{ΔI_E} $ の値は、ほぼ1です。(誤り)
答え (2)
電験三種の理論科目に出題される「電子回路」のページ
1.p型半導体とn型半導体
2.ダイオードとトランジスタの特性
3.トランジスタ増幅回路
4.トランジスタのバイアス回路
5.トランジスタの等価回路
6.FET増幅回路
7.多段・負帰還・電力増幅回路
8.オペアンプ(反転・非反転増幅回路)
9.発振回路と変調回路の原理
10.波形整形回路(クリッパ回路とリミッタ回路)






