第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の理論科目に出題される電界中の電子の運動について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の理論科目の試験で、実際に出題された電界中の電子の運動の過去問題も解説しています。
電界中における電子の運動
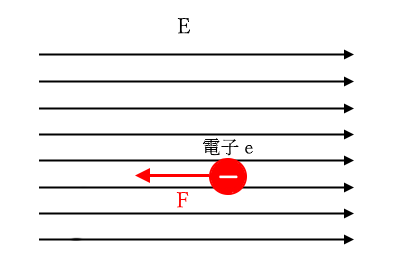
電界は大きさと向きを持つベクトルで表され、その強さは $E$[V/m]で表します。$E$[V/m]の電界中では、$e$[C]の電子は $eE$[N]の力を受けます。その方向は、電界とは逆向きになります。
電界 $E$ 中に置かれた電子 $e$ に働く力 $F$ を求める公式
$F=eE$[N]
$F$[N]:電界中の電子にはたらく力
$e$[C]:電子の電荷
$E$[V/m]:電界の強さ
(注)$e = 1.602×10^{-19}$
電界中に置かれた電子に働く力によって、電子 $e$[C]が移動するとき、電界 $E$[V/m]が電子 $e$[C]にする仕事 $W$[J]を考えてみます。(仕事)=(力の大きさ)×(移動距離)と定義されていますので、移動距離を $d$[m]とすると、次の関係式になります。
電子の移動による仕事を求める公式
$W=Fd=eEd$[J]
$W$[J]:仕事
$F$[N]:電界中の電子にはたらく力
$d$[m]:電子の移動距離
$e$[C]:電子の電荷
$E$[V/m]:電界の強さ
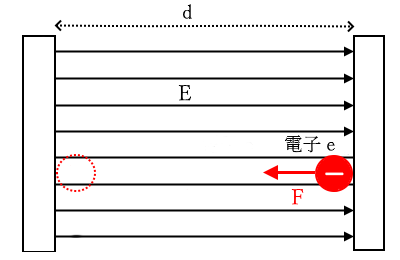
電界 $E$[V/m]はどこでも同じ「一様」ですので、移動距離 $d$[m]が決まれば、電子 $e$ [C]のする仕事 $W$[J]は電子のもつ電気量 $e$[C]に比例します。このときA点からB点に移動したとすれば、A点とB点が持つ位置エネルギー(電位)の差を「電位差」または「電圧」と定義し、$V$[V]で表します。
一様な電界 $E$ による電圧 $V$ の定義式
$V=Ed$[V]
$V$[V]:電位差
$E$[V/m]:電界の強さ
$d$[m]:距離
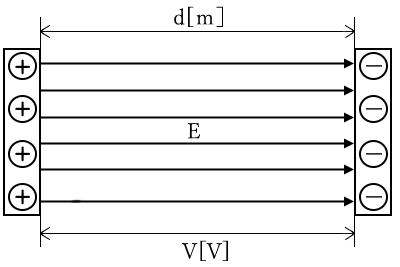
この電子が極に到着した時の速度を $v$ とすると、そのときの運動エネルギー $W$[J]は、次の公式で求めることができます。
運動エネルギー $W$ を求める公式
$W=\displaystyle\frac{mv^2}{2}$[J]
$W$[J]:電子の運動エネルギー
$m$[kg]:電子の質量
$v$[m/s]:電子の速度
電子の移動による仕事 $W=Fd=eEd$[J]と運動エネルギー $W=\displaystyle\frac{mv^2}{2}$[J]は等しくなりますので、
$e(Ed)=\displaystyle\frac{mv^2}{2}$
$eV=\displaystyle\frac{mv^2}{2}$
$v=\sqrt{\displaystyle\frac{2eV}{m}}$
また、電子が運動する力を $F’$[N]その時の、加速度を $a$[$m/s^2$]とすると、運動方程式より$F’=ma$[N]となります。この力は、電界 $E$[V/m]中に置かれた電子 $e$[C]に働く力 $F$[N]と同じものでなければなりません。したがって、
$F’=F$
$ma=eE$
$ma=\displaystyle\frac{eV}{d}$
$a=\displaystyle\frac{eV}{md}[m/s^2]$
電験三種-理論の過去問解説:電界中の電子の運動
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の理論科目で出題された問題です。
1997年(平成9年)問11【電験理論の過去問題】
真空中におかれた平行電極板間に、直流電圧 $V$[V]を加えて平等電界 $E$[V/m]を作り、この陰極板に電子をおいた場合、初速度零で出発した電子が陽極板に到達したときの速度は、$e$[m/s]となった。このときの電子の運動エネルギーは、電子が陽極板に到達するまでに得るエネルギーに等しいと考えられ、次の式が成立する。
$\displaystyle\frac{1}{2}mv^2=( ア )$
ただし、電子の電荷を $e$[C]、電子の質量を $m$[kg]とする。
したがって、この式から電子の速度 $v$[m/s]は、( イ )で表される。
上記の記述中の空白箇所(ア)及び(イ)に記入する字句として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | |
| (1) | $eE$ | $\displaystyle\sqrt{\frac{2eE}{m}}$ |
| (2) | $eV$ | $\displaystyle\sqrt{\frac{4eV}{m}}$ |
| (3) | $2eV$ | $\displaystyle\sqrt{\frac{4eV}{m}}$ |
| (4) | $eV$ | $\displaystyle\sqrt{\frac{2eV}{m}}$ |
| (5) | $eV$ | $\displaystyle\sqrt{\frac{4eV}{m}}$ |
真空中におかれた平行電極板間に、直流電圧 $V$[V]を加えて平等電界 $E$[V/m]を作り、この陰極板に電子をおいた場合、初速度零で出発した電子が陽極板に到達したときの速度は、$e$[m/s]となった。このときの電子の運動エネルギーは、電子が陽極板に到達するまでに得るエネルギーに等しいと考えられ、次の式が成立する。
$\displaystyle\frac{1}{2}mv^2=( eV )$
ただし、電子の電荷を $e$[C]、電子の質量を $m$[kg]とする。
したがって、この式から電子の速度 $v$[m/s]は、( $\displaystyle\sqrt{\frac{2eV}{m}}$ )で表される。
答え (4)
2003年(平成15年)問11【電験理論の過去問題】
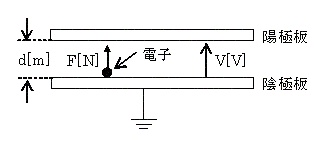
図のように、真空中に電極間隔 $d$[m]の平行板電極があり、陰極板上に電子を置いた。陽極板に電圧 $V$[V]を加えたとき、この電子に加わる力 $F$[N]の式として、正しいのは次のうちどれか。
ただし、電子の質量を $m$[kg]、電荷の絶対値を $e$[C]とする。また、電極板の端効果は無視できるものとする。
(1) $\displaystyle\frac{V^2}{d}e$ (2) $\displaystyle\frac{V}{d^2}em$ (3) $\displaystyle\frac{V}{d^2}\displaystyle\frac{m}{e}$ (4) $\displaystyle\frac{V}{d^2}e$ (5) $\displaystyle\frac{V}{d}e$
一様な電界 $E$[V/m]による電圧 $V$[V]の定義式は、
$V=Ed$[V]
電界 $E$[V/m]中に置かれた電子 $-e$[C]に働く力 $F$[N]は、
$F=eE$[N]
したがって、
$F=\displaystyle\frac{V}{d}e$[N]
答え (5)
2006年(平成18年)問12【電験理論の過去問題】
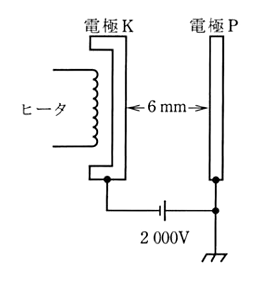
真空中において、図のように電極板の間隔が 6[mm]、電極板の面積が十分広い平行平板電極であり、電極K,P間には 2,000[V]の直流電圧が加えられている。このとき、電極K、P間の電界の強さは約( ア )[V/m]である。電極Kをヒータで加熱すると表面から( イ )が放出される。ある1個の電子に着目してその初速度を零とすれば、電子が電極Pに達したときの運動エネルギーWは( ウ )[J]となる。
ただし、電極K,P間の電界は一様とし、電子の電荷 $e=-1.6×10^{-19}$[C]とする。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句又は数値として、正しいものを組み合わせたのは次のうちどれか。
| (ア) | (イ) | (ウ) | |
| (1) | 3.3×102 | 光電子 | 1.6×10-16 |
| (2) | 3.3×105 | 熱電子 | 3.2×10-16 |
| (3) | 3.3×102 | 光電子 | 3.2×10-16 |
| (4) | 3.3×102 | 熱電子 | 1.6×10-16 |
| (5) | 3.3×105 | 熱電子 | 1.6×10-16 |
一様な電界 $E$[V/m]による電圧 $V$[V]の定義式は、
$V=Ed$[V]
$2000=E×6×10^{-3}$
$E=3.3×10^5$[V/m]
電界 $E$[V/m]が電子 $-e$[C]にする仕事 $W$[J]は、
$W=eV=1.6×10^{-19}×2000=3.2×10^{-16}$[J]
真空中において、図のように電極板の間隔が 6[mm]、電極板の面積が十分広い平行平板電極であり、電極K,P間には 2,000[V]の直流電圧が加えられている。このとき、電極K,P間の電界の強さは約( 3.3×105 )[V/m]である。電極Kをヒータで加熱すると表面から( 熱電子 )が放出される。ある1個の電子に着目してその初速度を零とすれば、電子が電極Pに達したときの運動エネルギーWは( 3.2×10-16 )[J]となる。
答え (2)
2007年(平成19年)問17【電験理論の過去問題】
直径 1.6[mm]の銅線中に 10[A]の直流電流が流れている。 この導線の長さ 1[m]あたりの自由電子の個数を $1.69×10^{23}$ 個、 自由電子1個の電気量を $-1.60×10^{-19}$[C]として、次の(a)及び(b)に答えよ。
なお、導体中の直流電流は自由電子の移動によってもたらされているとみなし、 その移動の方向は電流の方向と逆である。
また、 ある導体の断面を 1 秒間に 1[C]の割合で電荷が通過するときの電流の大きさが 1[A]と定義される。
(a) 10[A]の直流電流がながれているこの銅線の中を移動する自由電子の平均移動速度 $v$[m/s] の値として、最も近いのは次のうちどれか。
(1) $1.37×10^{-7}$ (2) $3.70×10^{-4}$ (3) $1.92×10^{-2}$ (4) $1.84×10^{2}$ (5) $3.00×10^{8}$
(b) この銅線と同じ材質の銅線の直径が 3.2[mm]、流れる電流が 30[A]であるとき、自由電子の平均移動速度[m/s]は左記(a)の速度の何倍になるか。その倍数として、最も近いのは次のうちどれか。
なお、銅線の単位体積当たりの自由電子の個数は同一である。
(1) 0.24 (2) 0.48 (3) 0.75 (4) 6.0 (5) 12
(a) 電流 1[A]は 1[C]の電荷が 1[s]間にある断面を 1[m]通過することです。つまり、
電流[A]=電荷量[C]×移動速度[m/s]
の関係になります。
全体の電荷量は、$-1.6×10^{19}×1.69×10^{23}$ ですので、移動速度を $v$[m/s]とすると、
$10[A]=-1.6×10^{19}×1.69×10^{23}[C]×v[m/s]$
$v=3.70×10^{-4}$
答え (2)
(b) 速度は電流に比例し、断面積に反比例します。直径は 4倍になり、電流は 3倍になりますので、速度は $\displaystyle\frac{3}{4}=0.75$ 倍になります。
答え (3)
2008年(平成20年)問12【電験理論の過去問題】
真空中において、電子の運動エネルギーが 400[eV]のときの速さが $1.19×10^7$[m/s]であった。電子の運動エネルギーが 100[eV]のときの速さ[m/s]の値として、正しいのは次のうちどれか。
ただし、電子の相対性理論効果は無視するものとする。
(1) $2.98×10^6$ (2) $5.95×10^6$ (3) $2.38×10^7$ (4) $2.98×10^9$ (5) $5.95×10^9$
電子の運動エネルギー $W$[J]は、
$W=\displaystyle\frac{1}{2}mv^2$[J]
電子の運動エネルギーが 400[eV]のときの速さが $1.19×10^7$[m/s]ですので、
$400=\displaystyle\frac{1}{2}m(1.19×10^7)^2$…(1)
電子の運動エネルギーが 100[eV]のときの速さを$v$[m/s]とすると、
$100=\displaystyle\frac{1}{2}mv^2$[J]…(2)
(1),(2)式を解くと、
$v=1.19×10^7×\sqrt{\displaystyle\frac{100}{400}}=5.95×10^6$[m/s]
答え (2)
2011年(平成23年)問12【電験理論の過去問題】
次の文章は、真空中における電子の運動に関する記述である。
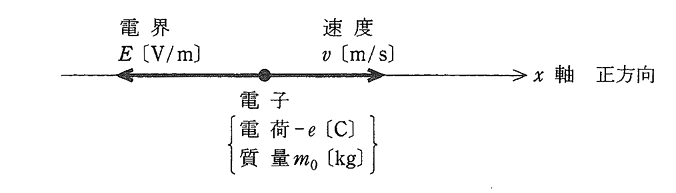
図のように、$x$ 軸上の負の向きに大きさが一定の電界 $E$[V/m]が存在しているとき、$x$ 軸上に電荷が $-e$[C]($e$は電荷の絶対値)、質量 $m_o$[kg]の1個の電子を置いた場合を考える。$x$ 軸の正方向の電子の加速度を $a$[$m/s^2$]とし、また、この電子に加わる力の正方向を $x$ 軸の正方向にとったとき、電子の運動方程式は
$m_oa$ =( ア )・・・・・①
となる。①式から電子は等加速度運動をすることがわかる。したがって、電子の初速度を零としたとき、$x$ 軸の正方向に向かう電子の速度 $v$[m/s]は時間 $t$[s]の( イ )関数となる。また、電子の走行距離$X_{dis}$[m]は時間 $t$[s]の( ウ )関数で表わされる。さらに、電子の運動エネルギーは時間 $t$[s]の( エ )で増加することがわかる。
ただし、電子の速度 $v$[m/s]はその質量の変化が無視できる範囲とする。
上記の記述中の空白個所(ア),(イ),(ウ)及び(エ)に当てはまる組み合わせとして、正しいものを次の(1)~(5)のうちから一つ選べ。
| (ア) | (イ) | (ウ) | (エ) | |
| (1) | $eE$ | 一次 | 二次 | 1乗 |
| (2) | $\displaystyle\frac{1}{2}eE$ | 二次 | 一次 | 1乗 |
| (3) | $eE^2$ | 一次 | 二次 | 2乗 |
| (4) | $\displaystyle\frac{1}{2}eE$ | 二次 | 一次 | 2乗 |
| (5) | $eE$ | 一次 | 二次 | 2乗 |
図のように、$x$ 軸上の負の向きに大きさが一定の電界 $E$[V/m]が存在しているとき、$x$ 軸上に電荷が $-e$[C]($e$は電荷の絶対値)、質量 $m_o$[kg]の1個の電子を置いた場合を考える。$x$ 軸の正方向の電子の加速度を $a$[$m/s^2$]とし、また、この電子に加わる力の正方向を $x$ 軸の正方向にとったとき、電子の運動方程式は
$m_oa$ =( $eE$ )・・・・・①
となる。①式から電子は等加速度運動をすることがわかる。したがって、電子の初速度を零としたとき、$x$ 軸の正方向に向かう電子の速度 $v$[m/s]は時間 $t$[s]の( 一次 )関数となる。また、電子の走行距離$X_{dis}$[m]は時間 $t$[s]の( 二次 )関数で表わされる。さらに、電子の運動エネルギーは時間 $t$[s]の( 2乗 )で増加することがわかる。
電子の運動方程式 $m_oa =eE$
速度 $v=at$ より電子の運動方程式に代入すると、時間 $t$[s]の一次関数となります。
走行距離 $\displaystyle\frac{1}{2}vt^2$ なので、時間 $t$[s]の二次関数となります。
運動エネルギー $\displaystyle\frac{1}{2}mv^2$ なので、時間 $t$[s]の 2乗で増加します。
答え (5)
2015年(平成27年)問12【電験理論の過去問題】
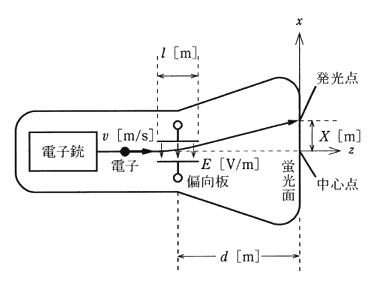
ブラウン管は電子銃、偏向板、蛍光面などから構成される真空管であり、オシロスコープの表示装置として用いられる。図のように、電荷 $-e$[C]をもつ電子が電子銃から一定の速度 $v$[m/s]で $z$ 軸に沿って発射される。電子は偏向板の中を通過する間、$x$ 軸に平行な平等電界 $E$ [V/m] から静電力 $-eE$[N]を受け、$x$ 方向の速度成分 $u$[m/s]を与えられ進路を曲げられる。偏向板を通過後の電子は $z$ 軸と $tanθ=\displaystyle\frac{u}{v}$なる角度 $θ$ をなす方向に直進して蛍光面に当たり、その点を発光させる。このとき発光する点は蛍光面の中心点から $x$ 方向に距離 $X $[m]だけシフトした点となる。
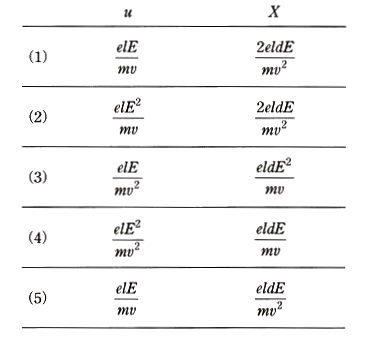
$u$ と $X$ を表す式の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、電子の静止質量を $m$[kg]、偏向板の $z$ 方向の大きさを $l $[m]、偏向板の中心から蛍光面までの距離を $d$[m]とし、$l≪d$ と仮定してよい。また、速度 $v$ は光速に比べて十分小さいものとする。
運動方程式より、
$F=ma=eE$
$a=\displaystyle\frac{eE}{m}$
偏光板を通過する時間 t は
$t=\displaystyle\frac{l}{v}$
したがって、偏光板を通過する間に加速された x 軸方向に進む速度 $u$ は
$u=at=\displaystyle\frac{elE}{mv}$
偏光板を通過したあとで蛍光面に到達するまでの時間は速度 $v$ で $d$ を通過する時間であり、その間 $u$ は x 軸方向に進み続けることになりますから、
$X=u×\displaystyle\frac{d}{v}=\displaystyle\frac{eldE}{mv^2}$
答え (5)
電験三種の理論科目に出題される「電気電子工学(電気の現象)」のページ
1.電気の単位と抵抗温度係数
2.電界中の電子の運動
3.ローレンツ力の向きと円運動
4.電子放出と熱起電力の原理
5.過渡現象と時定数とは




