第三種電気主任技術者(電験三種)試験に独学で合格できるよう、分野ごとに「考え方」や「解き方」の解説と過去問題をまとめています。このページで、電験三種の電力科目に出題される「力率補正と送電電力」について、初心者の方でも解りやすく、基礎から勉強できます。また、電験三種の電力科目の試験で、実際に出題された「力率補正と送電電力」の過去問題も解説しています。
交流電力の力率補正
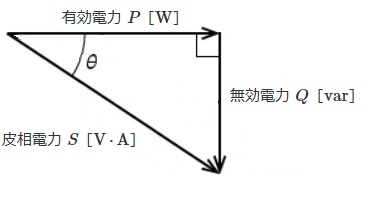
交流回路で実際に消費される電気エネルギーを有効電力といい、負荷と電源間で一時的に電磁エネルギーや静電エネルギーの形で蓄えられ、エネルギーが往復するだけで消費されない電力を無効電力といいます。また、有効電力と無効電力のベクトル和を、皮相電力といいます。
皮相電力に対する有効電力の割合を力率といいます。力率は cosθ で表し、θ を力率角といいます。
負荷にかかる電圧を V[V]、流れる電流を I[A]、力率を cosθとすると、有効電力 P[W]、無効電力 Q[var]、皮相電力 S[V⋅A]は次の式で表わすことができます。
単相の有効電力、無効電力、皮相電力を求める公式
有効電力:$P=VIcosθ$[W]
無効電力:$Q=VIsinθ$[var]
皮相電力:$S=VI$[V⋅A]
$V$「V]:電圧
$I$「A]:電流
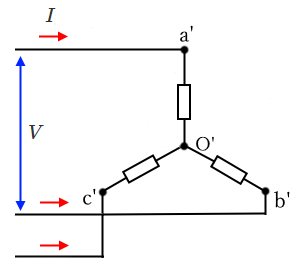
三相の有効電力、無効電力、皮相電力を求める公式
有効電力:$P=\sqrt{3}VIcosθ$[W]
無効電力:$Q=\sqrt{3}VIsinθ$[var]
皮相電力:$S=\sqrt{3}VI$[V⋅A]
$V$「V]:線間電圧
$I$「A]:線電流
ここでの三相電力を求める公式とは、三相負荷の消費電力を求める公式です。
力率改善
力率改善の計算は、有効電力 P[W]、無効電力 Q[var]、皮相電力 S[V⋅A]のベクトル図で示し、三平方の定理や三角関数を用いて計算します。
皮相電力、有効電力、無効電力の関係を表す式
$S^2=P^2+Q^2$
$S$[VA]:皮相電力
$P$[W]:有効電力
$Q$[Var]:無効電力
よく使う三角関数の公式です。
$sinθ=\sqrt{ 1-cos^2 θ}$
$tanθ=\displaystyle \frac{ sinθ }{ cosθ }=\displaystyle \frac{ \sqrt{ 1-cos^2 θ} }{ cosθ }$
三相3線式の送電電力
三相3線式送電線の送電端の相電圧を Es、受電端の相電圧を Er、線電流を I、線路のリアクタンスを X(線路抵抗は無視します)、負荷の力率を cosθ とすると、一相の送電電力 p[W]は次の式で求めることができます。
$p=ErIcosθ$[W]
三相全体の送電電力 $P$[W]は、この3倍となります。
$P=3ErIcosθ$[W]
ここで、一相分のベクトル図を示します。
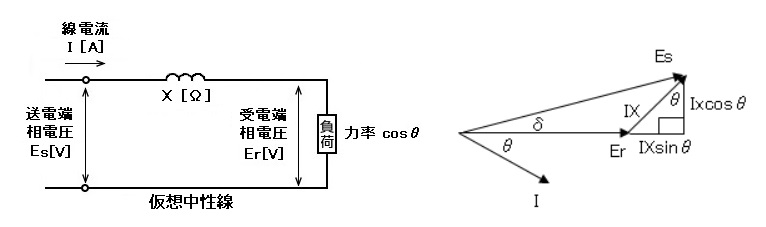
ベクトル図より、
$L=IXcosθ=Essinδ$
$Icosθ=\displaystyle \frac{ Essinδ }{ X }$
の関係が成り立ちます。sinδ の δ(読み:デルタ)は相差角といい、送電端と受電端の電圧の位相差です。この式を三相全体の送電電力 $P=3ErIcosθ$ の式に代入すると、次のようになります。
三相3線式の送電電力を求める式
$P=\displaystyle \frac{ 3EsEr }{ X }sinδ=\displaystyle \frac{ VsVr }{ X }sinδ$
Es:送電端の相電圧[V]
Er :受電端の相電圧[V]
Vs:送電端の線間電圧[V]
Vr:受電端の線間電圧[V]
X:線路リアクタンス[Ω]
δ:Es-Er間の相差角(電圧の位相差)
電験三種-電力の過去問解説:力率補正と送電電力
(財)電気技術者試験センターが作成した、第三種電気主任技術者試験の電力科目で出題された問題です。
2008年(平成20年)問16
電線1線の抵抗が 5[Ω]、誘導性リアクタンスが 6[Ω]である三相3線式送電線について、次の(a)及び(b)に答えよ。
(a) この送電線で受電端電圧を 60[kV]に保ちつつ、かつ、送電線での電圧降下率を受電端電圧基準で 10[%]に保つには、負荷の力率が 80[%](遅れ)の場合に受電可能な三相皮相電力[MV・A]の値として、最も近いのは次のうちどれか。
(1) 27.4 (2) 37,9 (3) 47.4 (4) 56.8 (5) 60.5
(b) この送電線の受電端に、遅れ力率 60[%]で三相皮相電力 63.2[MV・A]の負荷を接続しなければならなくなった。この場合でも受電端電圧を 60[kV]に、かつ、送電線での電圧降下率を受電端電圧基準で 10[%]に保ちたい。受電端に設置された調相設備から系統に供給すべき無効電力[Mvar]の値として、最も近いのは次のうちどれか。
(1) 12.6 (2) 15.8 (3) 18.3 (4) 22.1 (5) 34.8
2008年(平成20年)問16 過去問解説
電圧降下率を ε 、送電端電圧を Vs[kV]、受電端電圧を Vr[kV]とすると、
$ε=\displaystyle \frac{ Vs-Vr }{ Vr }×100$
$10=\displaystyle \frac{ Vs-60 }{ 60 }×100$
$Vs=66$[kV]
電圧降下を VL[V]とすると、近似式より
$V_L=Vs-Vr≒\sqrt{ 3 }I(rcosθ+xsinθ)$
$66000-60000≒\sqrt{ 3 }I(5×0.8+6×\sqrt{ 1-0.8^2 })$
$I=456$[A]
三相皮相電力 $S$[V・A]は
$S=\sqrt{ 3 }VrI=\sqrt{ 3 }×60000×456=47.4×10^6$[V・A]
答え (3)
(b) 遅れ力率 60[%]で三相皮相電力 63.2[MV・A]の負荷を接続した場合の、有効電力 P[MW]と無効電力 Q1[Mvar]は、
$P=Scosθ=63.2×0.6=37.92$[MW]
$Q_1=Ssinθ=63.2×\sqrt{ 1-0.6^2 }=50.56$[Mvar]
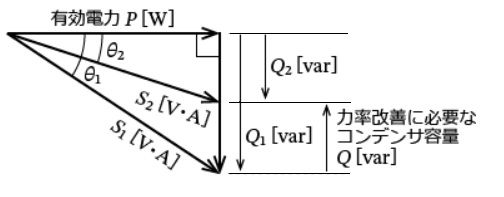
力率を改善するベクトル図を示します。
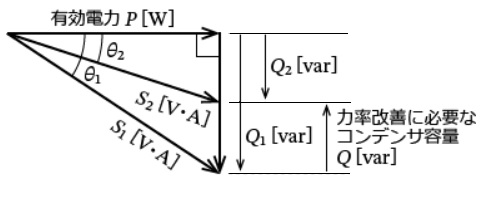
受電端電圧を 60[kV]に、かつ、送電線での電圧降下率を受電端電圧基準で 10[%]に保ちたいので、 ベクトル図より、S2=47.4 [MV・A]となります。力率改善に必要なコンデンサ容量を Q[Mvar]とすると、
$(Q_1-Q)^2=S_2^2-P^2$
$(50.56-Q)^2=47.4^2-37.92^2$
$Q≒22.1$[Mvar]
答え (4)
2009年(平成21年)問7
交流三相3線式1回線の送電線路があり、受電端に遅れ力率角 θ[rad]の負荷が接続されている。送電端の線間電圧を Vs[V]、受電端の線間電圧を Vr[V]、その間の相差角は δ[rad]である。
受電端の負荷に供給されている三相有効電力[W]を表す式として、正しいのは次のうちどれか。
ただし、送電端と受電端の間における電線1線あたりの誘導性リアクタンスは X[Ω]とし、線路の抵抗、静電容量は無視するものとする。
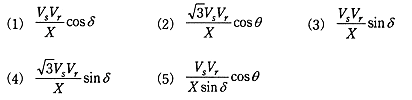
2009年(平成21年)問7 過去問解説
送電電力の公式
$P=\displaystyle \frac{ 3EsEr }{ X }sinδ=\displaystyle \frac{ VsVr }{ X }sinδ$
答え (3)
2009年(平成21年)問17
配電線に 100[kW]、遅れ力率 60[%]の三相負荷が接続されている。この受電端に 45[kvar]の電力用コンデンサを接続した。次の(a)および(b)に答えよ。
ただし、電力用コンデンサ接続前後の電圧は変わらないものとする。
(a) 電力用コンデンサを接続した後の受電端の無効電力[kvar]の値として、最も近いのは次のうちどれか。
(1) 56 (2) 60 (3) 75 (4) 88 (5) 133
(b) 電力用コンデンサ接続前と後の力率[%]の差の大きさして、最も近いのは次のうちどれか。
(1) 5 (2) 15 (3) 25 (4) 55 (5) 75
2009年(平成21年)問17 過去問解説
(a) 問題文をベクトル図で表示します。
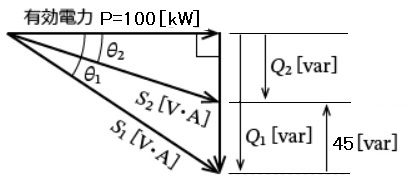
θ1=60°なので、
$\displaystyle \frac{ 100 }{ S_1 }=0.6$
$S_1≒166.7$[kV・A]
$Q_1=\sqrt{ S_1^2-P^2 }=\sqrt{ 166.7^2-100^2 }≒133.3$[kvar]
電力コンデンサ接続後の無効電力 Q2[kvar]は、
$Q_2=Q_1-45=133.3-45=88.3$[kvar]
答え (4)
(b) 電力コンデンサ接続後の皮相電力を S2[kV・A]とすると、
$S_2=\sqrt{ P^2+Q_2^2 }=\sqrt{ 100^2+88.3^2 }=133.4$[kV・A]
力率 cosθ2 は、
$cosθ_2=\displaystyle \frac{ P }{ S_2 }=\displaystyle \frac{ 100 }{133.4 }≒0.75$
よって力率の差は
$75-60=15$[%]
答え (2)
2010年(平成22年)問6
50[Hz],200[V]の三相配電線の受電端に、力率 0.7,50[kW]の誘導性三相負荷が接続されている。この負荷と並列に三相コンデンサを挿入して、受電端での力率を遅れ 0.8 に改善したい。
挿入すべき三相コンデンサの無効電力容量[kV・A]の値として、最も近いのは次のうちどれか。
(1)4.58 (2)7.80 (3)13.5 (4)19.0 (5)22.5
2010年(平成22年)問6 過去問解説
問題文をベクトル図で表示します。
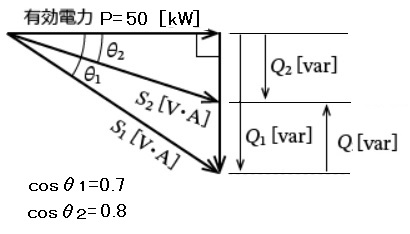
コンデンサを挿入前の皮相電力 S1 と 無効電力 Q1 は、
$\displaystyle \frac{ 50 }{ S_1 }=0.7$
$S_1=71.43$[kVA]
$Q_1=\sqrt{ S_1^2-P^2 }=\sqrt{ 71.43^2-50^2 }≒51.01$[kvar]
コンデンサを挿入後の皮相電力 S2 と 無効電力 Q2 は、
$\displaystyle \frac{ 50 }{ S_2 }=0.7$
$S_2=62.5$[kVA]
$Q_2=\sqrt{ S_2^2-P^2 }=\sqrt{ 62.5^2-50^2 }≒37.5$[kvar]
挿入すべき三相コンデンサの無効電力容量 Q[kV・A]は、
$Q=Q_1-Q_2=51.01-37.5=13.51$[kV・A]
答え (3)
2012年(平成24年)問17
定格容量 750[kV・A]の三相変圧器に遅れ力率 0.9 の三相負荷 500[kW]が接続されている。この三相変圧器に新たに遅れ力率 0.8 の三相負荷 200[kW]を接続する場合、次の(a)及び(b)の問に答えよ。
(a) 負荷を追加した後の無効電力[kvar]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 339 (2) 392 (3) 472 (4) 525 (5) 610
(b) この変圧器の過負荷運転を回避するために、変圧器の二次側に必要な最小の電力用コンデンサ容量[kvar]の値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 50 (2) 70 (3) 123 (4) 203 (5) 256
2012年(平成24年)問17 過去問解説
(a) 問題文をベクトル図で表示します。
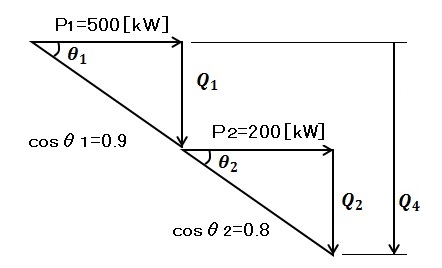
はじめの負荷の無効電力を Q1[kvar]、追加した負荷の無効電力を Q2[kvar]とすると、
$Q_1=P_1tanθ_1=500×\displaystyle \frac{ \sqrt{ 1-0.9^2 } }{ 0.9 }≒242$[kvar]
$Q_2=P_2tanθ_2=200×\displaystyle \frac{ \sqrt{ 1-0.8^2 } }{ 0.8 }=150$[kvar]
負荷を追加した後の無効電力 Q4[kvar]は、
$Q_4=Q_1+Q_2=242+150=392$[kvar]
答え (2)
(b) 問題文をベクトル図で表示します。
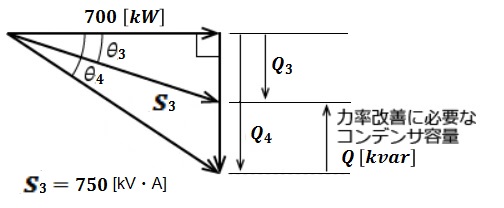
皮相電力が 750[kV・A]になるときの無効電力 Q3 は、
$Q_3=\sqrt{ 750^2-700^2}≒269$[kvar]
力率改善に必要なコンデンサ容量 Q は、
$Q=Q_4-Q_3=392-269=123$[kvar]
答え (3)
2013年(平成25年)問16
図のように、特別高圧三相 3 線式 1 回線の専用架空送電路で受電している需要家がある。需要家の負荷は、40 [MW]、力率が遅れ 0.87 で、需要家の受電端電圧は 66[kV] である。
ただし、需要家から電源側をみた電源と専用架空送電線路を含めた百分率インピーダンスは、基準容量 10 [MV・A] 当たり 6.0 [%] とし、抵抗はリアクタンスに比べ非常に小さいものとする。その他の定数や条件は無視する。
次の(a)及び(b)の問に答えよ。
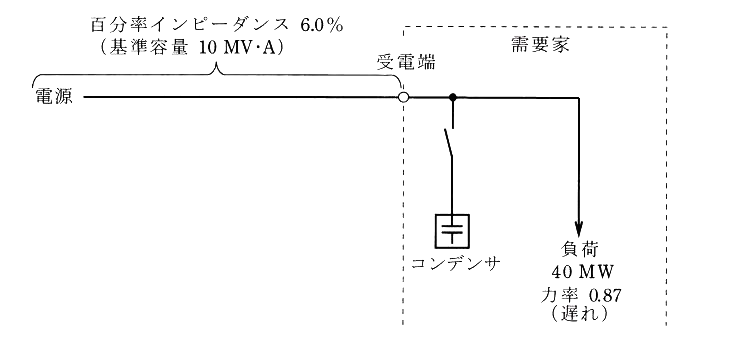
(a) 需要家が受電端において、力率 1 の受電になるために必要なコンデンサ総容量[Mvar]の値として、
最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、受電端電圧は変化しないものとする。
(1) 9.7 (2) 19.7 (3) 22.7 (4) 34.8 (5) 81.1
(b) 需要家のコンデンサが開閉動作を伴うとき、受電端の電圧変動率を 2.0[%]以内にするために必要な
コンデンサ単機容量 [Mvar] の最大値として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.46 (2) 1.9 (3) 3.3 (4) 4.3 (5) 5.7
2013年(平成25年)問16 過去問解説
(a) 問題文をベクトル図で表示します。
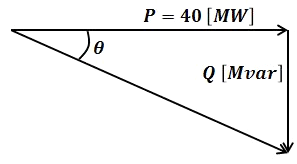
無効電力 Q[Mvar]のコンデンサ を接続すると力率が 1 になりますので、
$Q=Ptanθ=P\displaystyle \frac{ \sqrt{ 1-cos^2 θ} }{ cosθ }$
$=40×\displaystyle \frac{ \sqrt{ 1-0.87^2 } }{0.87 }≒22.7$[Mvar]
答え (3)
(b) コンデンサ単機とは、無負荷のことです。つまり、無負荷時の電圧降下 VL を電圧変動率 2.0[%]以内に収めるためのコンデンサ容量 Q を求めます。
$P=\sqrt{ 3 }VrIcosθ$
$cosθ=\displaystyle \frac{P} {\sqrt{ 3 }VrI }$
$Q=\sqrt{ 3 }VrIsinθ$
$sinθ=\displaystyle \frac{Q} {\sqrt{ 3 }VrI }$
電線1線当たりの抵抗 r[Ω]、リアクタンス x[Ω]とすると電圧降下 VL は、
$V_L≒\sqrt{ 3 }I(rcosθ+xsinθ)$
$≒\sqrt{ 3 }I(r×\displaystyle \frac{P} {\sqrt{ 3 }VrI }+x×\displaystyle \frac{Q} {\sqrt{ 3 }VrI })$
$≒\displaystyle \frac{rP+xQ} {Vr }$
抵抗はリアクタンスに比べ非常に小さいので、r=0 として考えます。
$V_L≒\displaystyle \frac{xQ} {Vr }$
$Q=\displaystyle \frac{V_LVr} {x }$
百分率リアクタンス(インピーダンス)は、$\%x=\displaystyle \frac{P_bx}{ V_b^2 }×100$[%]ですので、
$x=\displaystyle \frac{V_b^2}{P_b }×\displaystyle \frac{\%x}{100 }=\displaystyle \frac{(66×10^3)^2}{10×10^6 }×\displaystyle \frac{6}{100 }≒26.1$[Ω]
電圧降下率 ε=2.0 なので、
$ε=\displaystyle \frac{ V_L }{ Vr }×100$[%]
$2=\displaystyle \frac{ V_L }{ 66×10^3 }×100$
$V_L=13.2×10^2$
よって、コンデンサ容量 Q は、
$Q=\displaystyle \frac{V_LVr} {x }=\displaystyle \frac{13.2×10^2×66×10^3} {26.1 }=3.34×10^6$[var]
答え (3)
2015年(平成27年)問17
図に示すように、線路インピーダンスが異なるA、B回線で構成される 154kV 系統があったとする。A回線側にリアクタンス 5% の直列コンデンサが設置されているとき、次の(a)及び(b)の問に答えよ。なお、系統の基準容量は、10MV・Aとする。
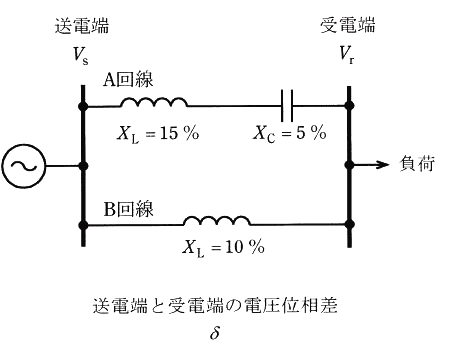
(a) 図に示す系統の合成線路インピーダンスの値[%]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 3.3 (2) 5.0 (3) 6.0 (4) 20.0 (5)30.0
(b) 送電端と受電端の電圧位相差δが 30度 であるとき、この系統での送電電力 P の値 [MW] として、最も近いものを次の(1)~(5)のうちから一つ選べ。ただし、送電端電圧 Vs、受電端電圧 Vr は、それぞれ 154kV とする。
(1) 17 (2) 25 (3) 83 (4) 100 (5) 152
2015年(平成27年)問17 過去問解説
(a) 基準容量が一致しているのそのまま合成%インピーダンス( %Z )を計算できます。
$\%Z=\displaystyle \frac{ (15-5)×10 }{(15-5)+10}=5$[%]
答え (2)
(b) 線間電圧を Vb[V]、基準容量を Pb とすると、
$\%Z=\displaystyle \frac{P_bZ}{ V_b^2 }×100$[%]
$Z=\displaystyle \frac{\%ZV_b^2}{ 100P_b }=X$
$X=\displaystyle \frac{5×154^2}{ 100×10 }≒118.6$[Ω]
送電電力 $P$ は、
$\begin{eqnarray}P&=&\displaystyle \frac{ VsVr }{ X }sinδ\\\\&=&\displaystyle \frac{ 154^2×154^2 }{ 118.6 }sin30°≒100×10^6\end{eqnarray}$
答え (4)
2017年(平成29年)問17
特別高圧三相3線式専用1回線で、6000kW(遅れ力率90%)の負荷Aと 3000kW(遅れ力率95%)の負荷Bに受電している需要家がある。
次の(a)及び(b)の問に答えよ。
(a) 需要家全体の合成力率を 100% にするために必要な力率改善用コンデンサの総容量の値[kvar]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
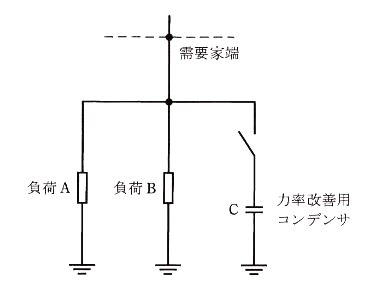
(1) 1430 (2) 2900 (3) 3550 (4) 3900 (5) 4360
(b) 力率改善用コンデンサの投入・開放による電圧変動を一定値に抑えるために力率改善用コンデンサを分割して設置・運用する。下図のように分割設置する力率改善用コンデンサのうちの1台(C1)は容量が 1000kvar である。C1を投入したとき、投入前後の需要家端Dの電圧変動率が 0.8% であった。需要家端Dから電源側を見たパーセントインピーダンスの値[%](10MV・Aベース)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、線路インピーダンス X はリアクタンスのみとする。また、需要家構内の線路インピーダンスは無視する。
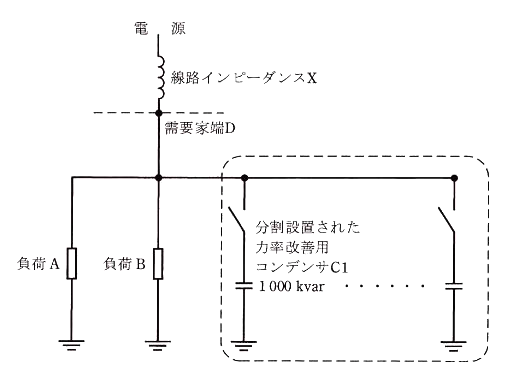
(1) 1.25 (2) 8.00 (3) 10.0 (4) 12.5 (5) 15.0
2017年(平成29年)問17 過去問解説
(a) 負荷A、負荷Bの電力ベクトル図を示します。
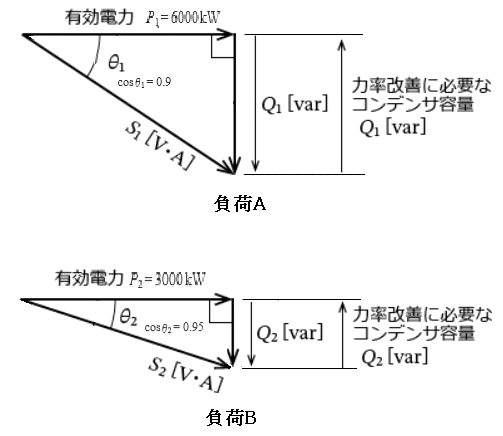
負荷A,Bの力率改善に必要なコンデンサ容量 Q1,Q2[var]は、
$\begin{eqnarray}Q_1&=&P_1tanθ=P_1\displaystyle \frac{ \sqrt{ 1-cos^2 θ} }{ cosθ }\\\\&=&6000×10^3×\displaystyle \frac{ \sqrt{ 1-0.9^2 } }{0.9 }\\\\&=&2906×10^3[var]\end{eqnarray}$
$\begin{eqnarray}Q_2&=&P_2tanθ=P_2\displaystyle \frac{ \sqrt{ 1-cos^2 θ} }{ cosθ }\\\\&=&3000×10^3×\displaystyle \frac{ \sqrt{ 1-0.95^2 } }{0.95 }\\\\&=&986×10^3[var]\end{eqnarray}$
力率改善に必要なコンデンサの総容量 Q[kvar]は
$Q=Q_1+Q_2=2906+986=3892$[kvar]
答え (4)
(b) 線間電圧を Vn[V]、力率改善用コンデンサC1を投入したときの無効電力を QC1 とすると、
$Q_{C1}=\sqrt{ 3 }V_nIsinθ$
$\displaystyle \frac{ Q_{C1} }{ V_n }=\sqrt{ 3 }Isinθ$
電圧降下を VL[V]とすると、線路インピーダンス X はリアクタンスのみなので、
$V_L=\sqrt{ 3 }I(rcosθ+xsinθ)=\sqrt{ 3 }IXsinθ=\displaystyle \frac{ XQ_{C1} }{ V_n }$
基準容量を P[V・A]とすると、$P=\sqrt{ 3 }V_nI_n$ ですので、百分率インピーダンス %X は、次の式に変形することができます。
$\begin{eqnarray}\%X &=& \displaystyle \frac{ \sqrt{ 3 }I_nX }{V_n}×100 \\\\ &=&\displaystyle \frac{ \sqrt{ 3 }I_nX ×V_n}{V_n×V_n}×100 \\\\ &=&\displaystyle \frac{ PX }{V_n^2}×100\end{eqnarray}$
$X=\displaystyle \frac{ \%XV_n ^2 }{ P×100 }$[%]
電圧変動率を ε とすると、
$ε=\displaystyle \frac{ V_L }{ V_n }×100=\displaystyle \frac{ XQ_{C1} }{ V_n ^2}×100$[%]
X を %X で表すと、
$ε=\displaystyle \frac{ XQ_{C1} }{ V_n ^2}×100=\displaystyle \frac{ \%XQ_{C1} }{ P×100}×100$[%]$0.8=\displaystyle \frac{ \%X×1000×10^3 }{ 10×10^6}$
$\%X=8.0$[%]
答え (2)
電験三種の電力科目に出題される「配電線路」のページ






